Bài giảng Nhập môn mạch số - Chương 5, Phần 2: Mạch tổ hợp. Các loại mạch khác - Hồ Ngọc Diễm
Mạch giải mã (Decoder)
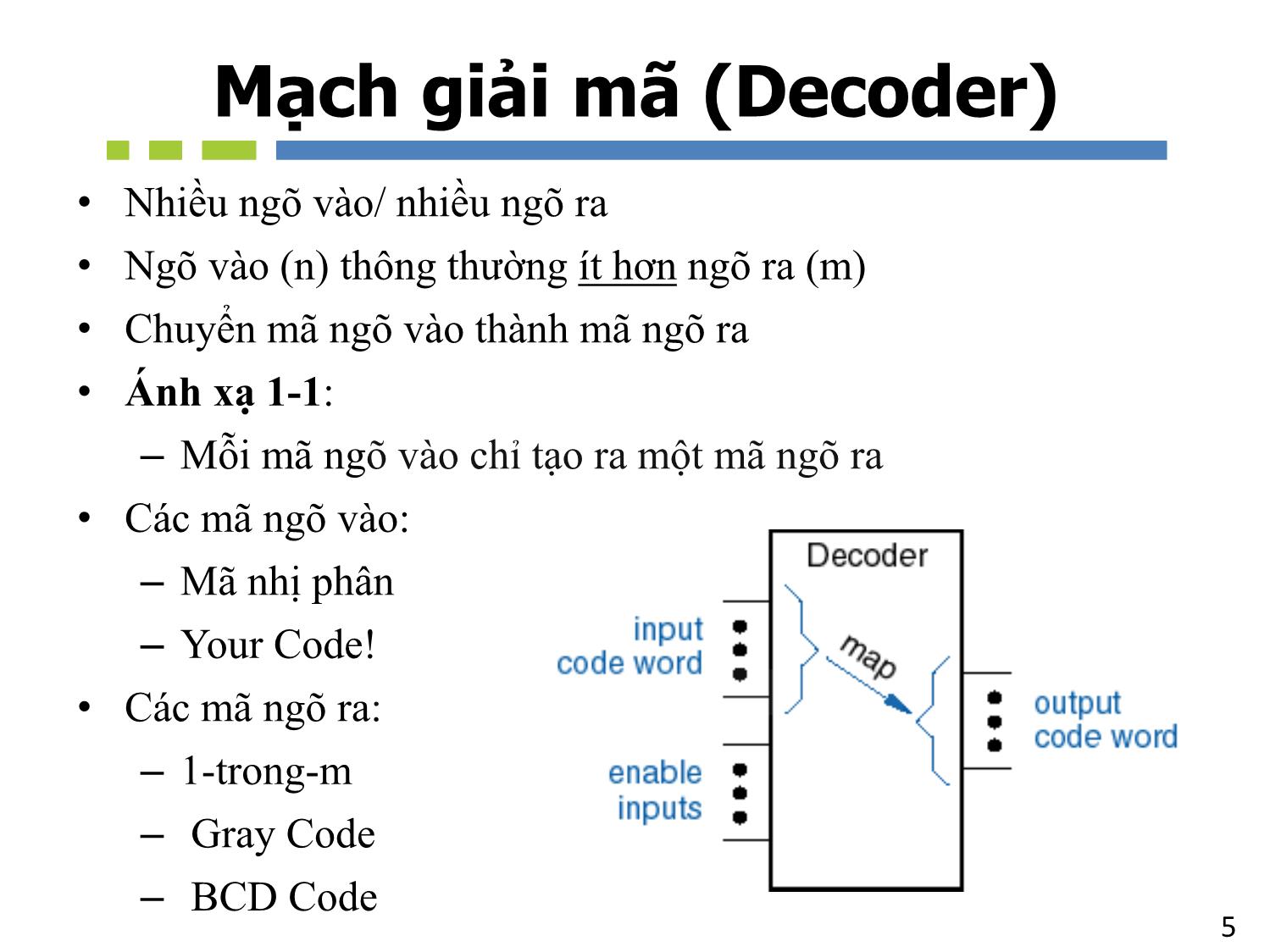
• Nhiều ngõ vào/ nhiều ngõ ra
• Ngõ vào (n) thông thường ít hơn ngõ ra (m)
• Chuyển mã ngõ vào thành mã ngõ ra
• Ánh xạ 1-1:
– Mỗi mã ngõ vào chỉ tạo ra một mã ngõ ra
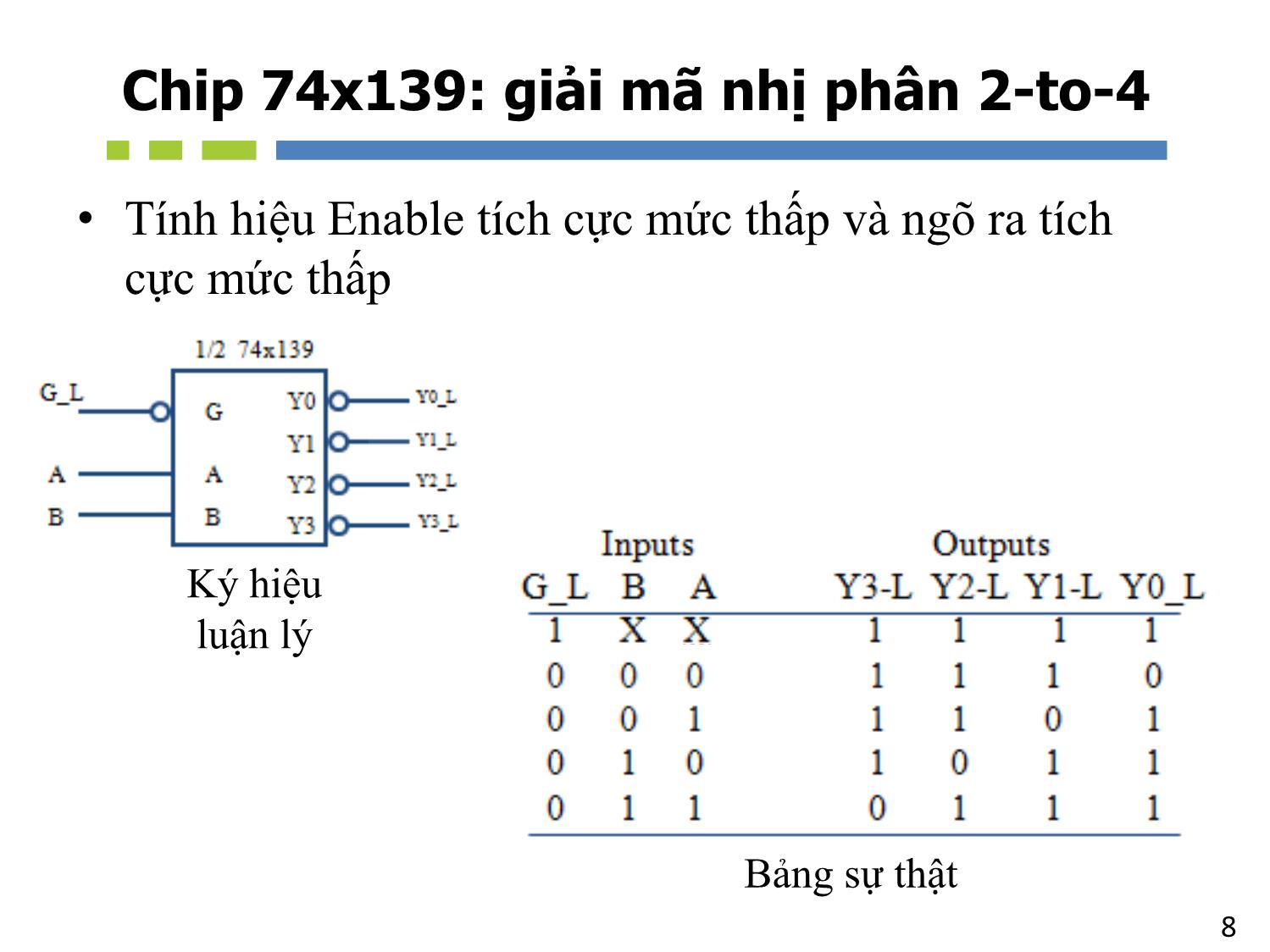
• Các mã ngõ vào:
– Mã nhị phân
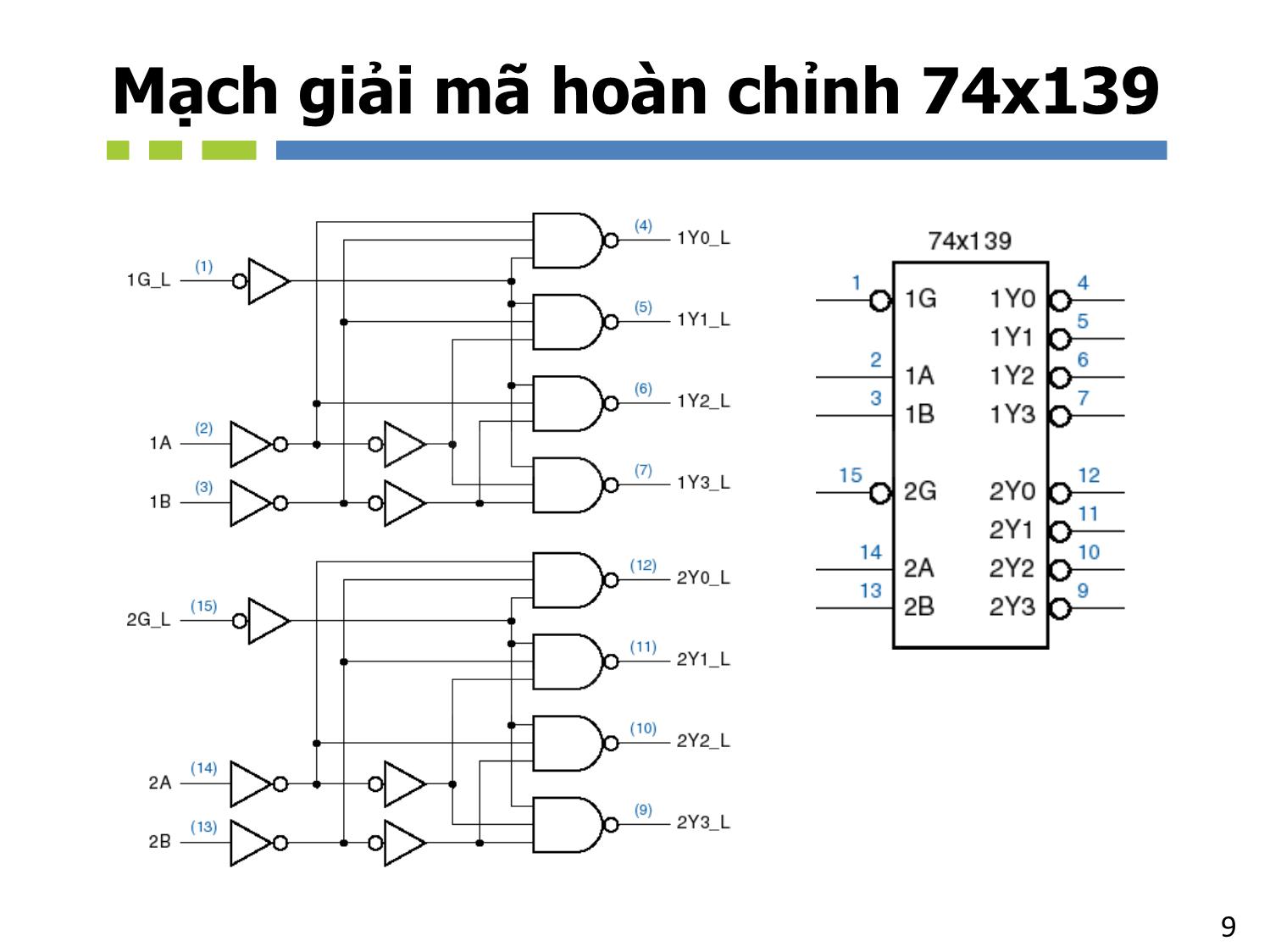
– Your Code!
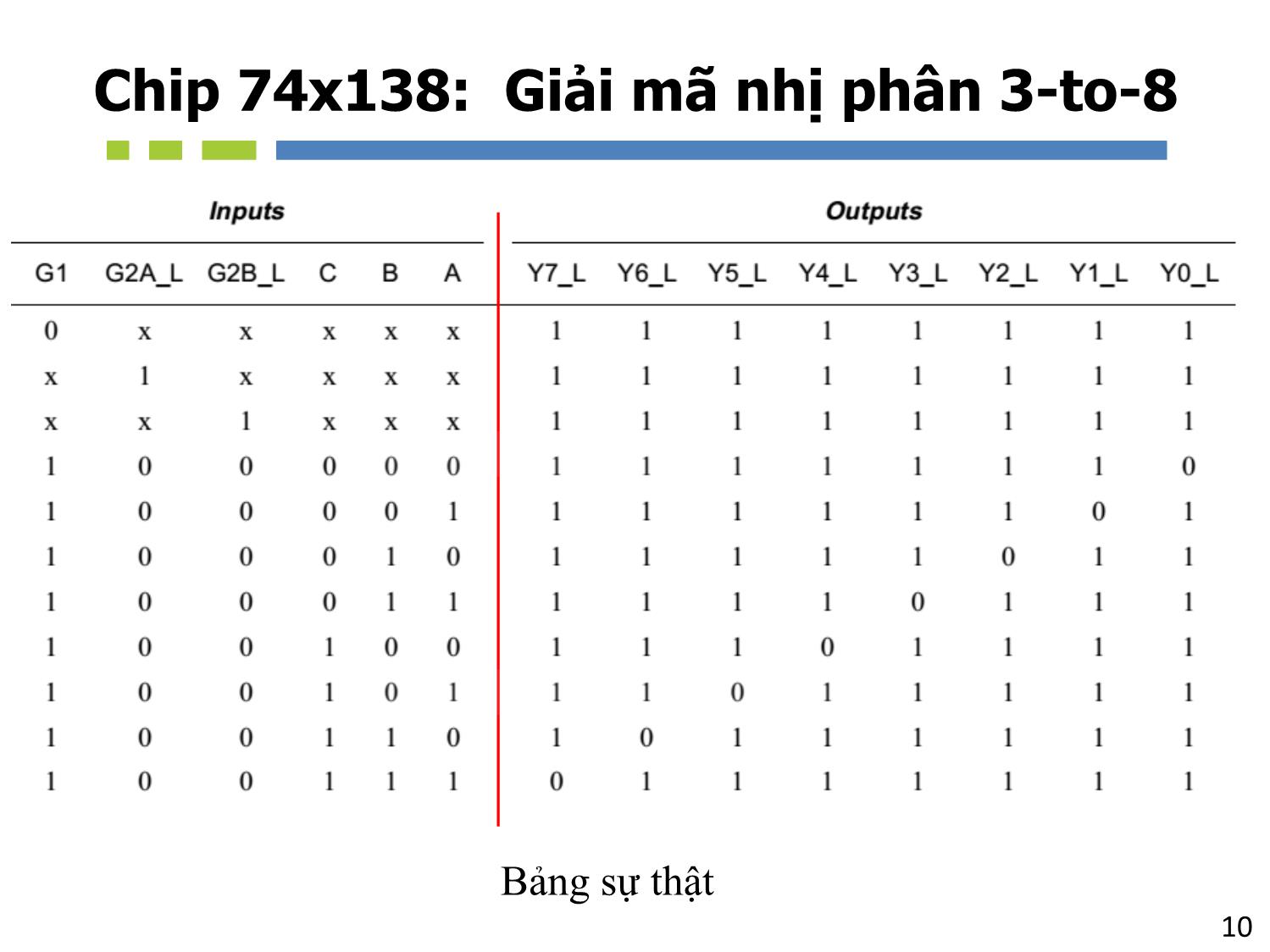
• Các mã ngõ ra:
– 1-trong-m
– Gray Code
– BCD Code
Mạch giải mã nhị phân
(Binary Decoders)
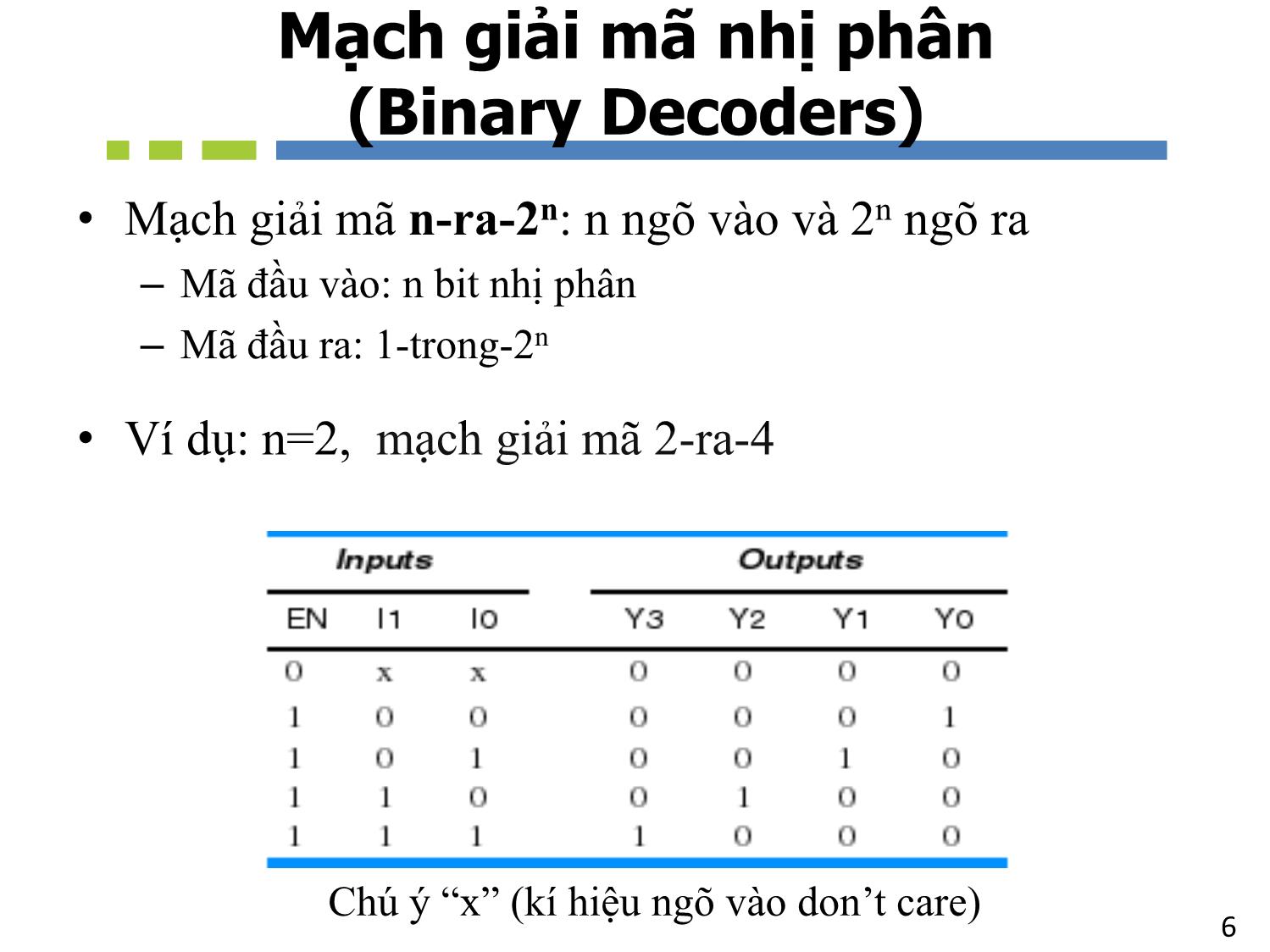
• Mạch giải mã n-ra-2n: n ngõ vào và 2n ngõ ra
– Mã đầu vào: n bit nhị phân
– Mã đầu ra: 1-trong-2n
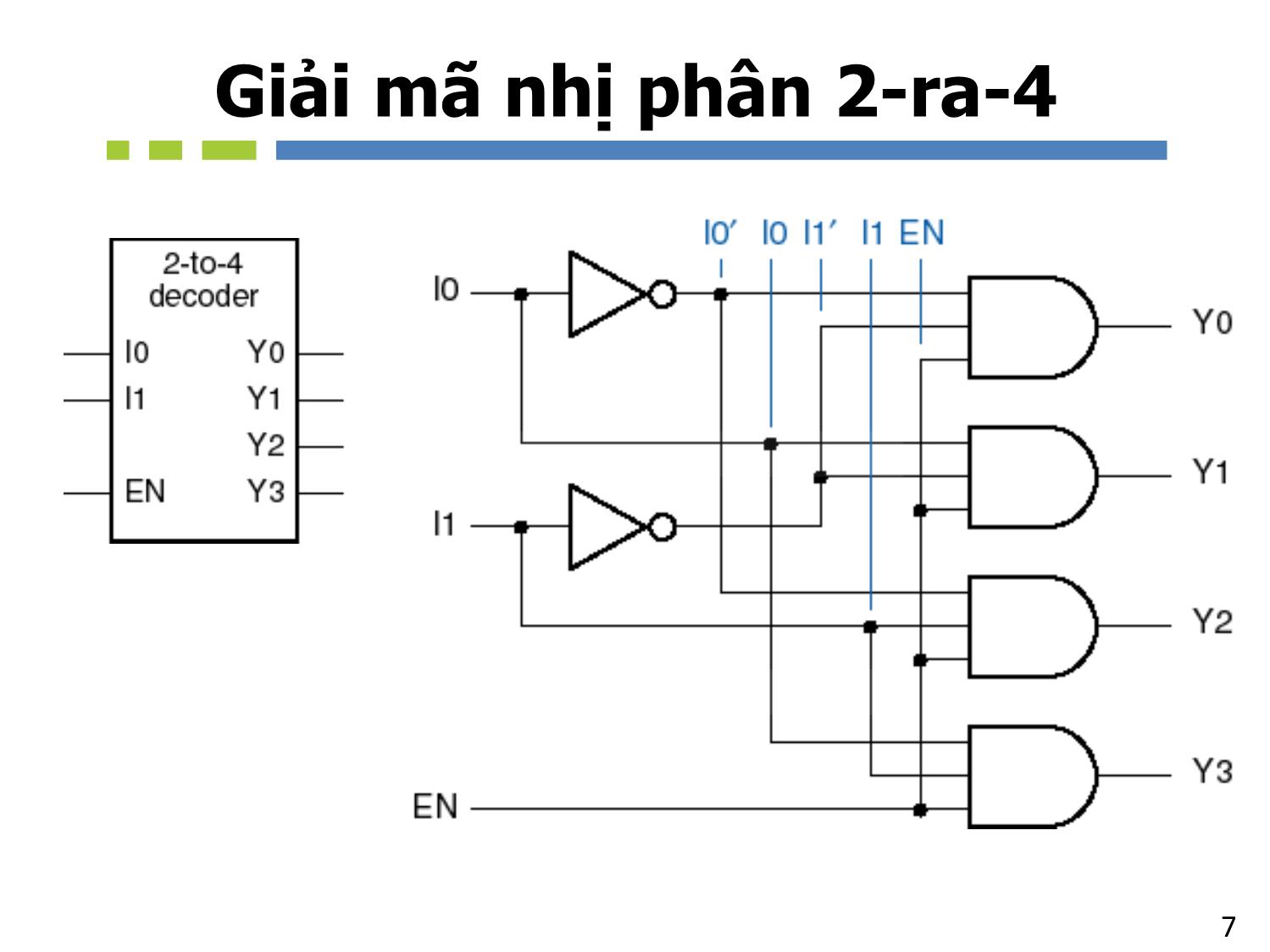
• Ví dụ: n=2, mạch giải mã 2-ra-4

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Nhập môn mạch số - Chương 5, Phần 2: Mạch tổ hợp. Các loại mạch khác - Hồ Ngọc Diễm", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Nhập môn mạch số - Chương 5, Phần 2: Mạch tổ hợp. Các loại mạch khác - Hồ Ngọc Diễm

1Chương 5 – phần 2 NHẬP MÔN MẠCH SỐ Mạch tổ hợp: Các loại mạch khác 2Nội dung 1. Mạch cộng (Carry Ripple (CR) Adder) 2. Mạch cộng nhìn trước số nhớ - (Carry Look-Ahead (CLA) Adder) 3. Mạch cộng/ mạch trừ 4. Đơn vị tính toán luận lý (Arithmetic Logic Unit) 5. Mạch giải mã (Decoder)/ Mạch mã hoá (Encoder) 6. Mạch dồn kênh (Multiplexer)/ Mạch chia kênh (Demultiplexer) 7. Mạch tạo Parity/ Mạch kiểm tra Parity 8. Mạch so sánh (Comparator) 3Nội dung 1. Mạch cộng (Carry Ripple (CR) Adder) 2. Mạch cộng nhìn trước số nhớ - (Carry Look-Ahead (CLA) Adder) 3. Mạch cộng/ mạch trừ 4. Đơn vị tính toán luận lý (Arithmetic Logic Unit) 5. Mạch giải mã (Decoder)/ Mạch mã hoá (Encoder) 6. Mạch dồn kênh (Multiplexer)/ Mạch chia kênh (Demultiplexer) 7. Mạch tạo Parity/ Mạch kiểm tra Parity 8. Mạch so sánh (Comparator) 45. Decoder/ Encoder 5Mạch giải mã (Decoder) • Nhiều ngõ vào/ nhiều ngõ ra • Ngõ vào (n) thông thường ít hơn ngõ ra (m) • Chuyển mã ngõ vào thành mã ngõ ra • Ánh xạ 1-1: – Mỗi mã ngõ vào chỉ tạo ra một mã ngõ ra • Các mã ngõ vào: – Mã nhị phân – Your Code! • Các mã ngõ ra: – 1-trong-m – Gray Code – BCD Code enable inputs 6Mạch giải mã nhị phân (Binary Decoders) • Mạch giải mã n-ra-2n: n ngõ vào và 2n ngõ ra – Mã đầu vào: n bit nhị phân – Mã đầu ra: 1-trong-2n • Ví dụ: n=2, mạch giải mã 2-ra-4 Chú ý “x” (kí hiệu ngõ vào don’t care) 7Giải mã nhị phân 2-ra-4 8Chip 74x139: giải mã nhị phân 2-to-4 • Tính hiệu Enable tích cực mức thấp và ngõ ra tích cực mức thấp Bảng sự thật Ký hiệu luận lý 9Mạch giải mã hoàn chỉnh 74x139 10 Chip 74x138: Giải mã nhị phân 3-to-8 Bảng sự thật 11 74x138 Ký hiệu luận lý Mạch luận lý 12 Ghép mạch giải mã Mạch giải mã 4-to-16 13 Ứng dụng của mạch giải mã • Một ứng dụng phổ biến là giải mã địa chỉ cho các chip nhớ 14 Giải mã BCD ra LED 7 đoạn 15 LED 7 đoạn (7-segment display) • LED 7 đoạn là cách phổ biến để hiển thị số thập phân hoặc số thập lục phân – Sử dụng LED cho mỗi đoạn 16 LED 7 đoạn (7-segment display) Bằng cách điều khiển dòng điện qua mỗi LED, một số đoạn sẽ sáng và một số tắt, từ đó tạo nên số mong muốn 17 Giải mã BCD ra LED 7 đoạn Chuyển số BCD sang thông tin thích hợp để hiển thị trên đèn 7 đoạn 18 Mạch mã hoá (Encoder) • Nhiều ngõ vào/ nhiều ngõ ra • Chức năng ngược lại với mạch giải mã • Outputs (m) ít hơn inputs (n) • Chuyển mã ngõ vào thành mã ngõ ra input code output code ENCODER 19 Encoders vs. Decoders Decoder Encoder 2^n-ra-n Input code: 1-trong-2^n Output code: Mã nhị phân n-ra-2^n Input code: Mã nhị phân Output code:1-trong-2^n decoders/encoders nhị phân 20 Mạch mã hoá nhị phân (Binary Encoder) • 2^n-ra-n encoder: 2^n ngõ vào và n ngõ ra – Input code: 1-trong-2^n – Output code: Mã nhị phân Ví dụ: n=3, mạch mã hóa 8-ra-3 Bảng sự thật Ký hiệu 21 Hiện thực mạch mã hóa 8-ra-3 • Rút gọn: Y0 = I1 + I3 + I5 + I7 Y1 = I2 + I3 + I6 + I7 Y2 = I4 + I5 + I6 + I7 I1 I2 I3 I4 I5 I6 I0 I7 Y1 Y0 Y2 Ngõ vào Ngõ ra I0 I1 I2 I3 I4 I5 I6 I7 Y2 Y1 Y0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 1 1 1 1 22 Hiện thực mạch mã hóa 8-ra-3 • Giới hạn: – I0 không ảnh hưởng đến ngõ ra – Chỉ một ngõ nhập được kích hoạt tại một thời điểm • Ứng dụng: – Giải quyết những yêu cầu từ nhiều thiết bị, nhưng không phải là những yêu cầu đồng thời. – Trong trường hợp có nhiều thiết bị yêu cầu cùng lúc thì có thể thiết lập mức độ ưu tiên để giải quyết vấn đề này. I1 I2 I3 I4 I5 I6 I0 I7 Y1 Y0 Y2 23 Cần có độ ưu tiên trong hầu hết các ứng dụng 24 Mạch mã hoá có độ ưu tiên (Priority Encoder) • Gán độ ưu tiên cho các ngõ vào • Khi có nhiều hơn 1 ngõ vào tích cực, ngõ ra tạo ra mã của ngõ vào có độ ưu tiên cao nhất. • Priority Encoder: H7=I7 (Độ ưu tiên cao nhất) H6=I6.I7’ H5=I5.I6’.I7’ H4=I4.I5’.I6’.I7’ H3=I3.I4’.I5’.I6’.I7’ H2=I2.I3’.I4’.I5’.I6’.I7’ H1=I1. I2’.I3’.I4’.I5’.I6’.I7’ H0=I0.I1’. I2’.I3’.I4’.I5’.I6’.I7’ IDLE= I0’.I1’. I2’.I3’.I4’.I5’.I6’.I7’ • Encoder A0=Y0 = H1 + H3 + H5 + H7 A1=Y1 = H2 + H3 + H6 + H7 A2=Y2 = H4 + H5 + H6 + H7 I6 I5 I4 Y1 Y0I3 I2 I1 I7 Y2 I0 Binary encoder I6 I5 I4 I3 I2 I1 I7 I0 Priority Circuit H6 H5 H4 H3 H2 H1 H7 H0 IDLE I6 I5 I4 I3 I2 I1 I7 I0 A1 A0 A2 IDLE Priority encoder 25 8-input priority encoder • I7 có độ ưu tiên cao nhất, I0 thấp nhất • A2-A0 chứa số thứ tự của ngõ vào có độ ưu tiên cao nhất đang tích cực • IDLE tích cực nếu không có ngõ vào nào tích cực 26 74x148 8-input priority encoder – Các pin trên chip đều tích cực mức thấp GS: Got Something/Group Select EO: Enable Output 27 74x148 – Bảng sự thật 28 74x148 28 Sơ đồ luận lý 29 Ghép các priority encoders Mạch mã hoá có độ ưu tiên 32-ngõ vào được ghép từ 4 mạch mã hóa ưu tiên 8-ngõ vào 30 6. Multiplexer (MUX)/ Demultiplexer (DeMUX) 31 Multiplexer (MUX) • Một MUX truyền một trong những ngõ vào của nó ra ngõ ra dựa trên tín hiệu Select Ngõ vào SELECT sẽ xác định ngõ vào nào được truyền ra Z 32 2-to-1 Multiplexer Sel Out 0 I0 1 I1 Out =Sel * I0 + Sel * I1 Ký hiệu Biểu thức đại số Mạch logic Minh họa với Sel = 0 33 4-to-1 Mux • 4-to-1 Mux xuất ra một trong bốn ngõ vào dựa trên giá trị của 2 tín hiệu select Ký hiệu Bảng sự thật Biểu thức đại số 34 Xây dựng MUX 4-to-1 • Từ MUX 2-to-1 35 Chip 74x151: 1-bit multiplexer 8-to-1 Bảng sự thật Ký hiệu Sơ đồ luận lý 36 Demultiplexer • Demultiplexer (DEMUX) lấy ngõ vào duy nhất và phân phối nó ra một ngõ ra. – Mã ngõ vào SELECT sẽ xác định ngõ ra nào sẽ được kết nối với ngõ vào DATA được truyền ra một và chỉ một ngõ ra được xác định bởi mã của ngõ vào SELECT 37 DEMUX 1-to-8 demultiplexer Chú ý: I là ngõ vào DATA 38 Tổng hợp các hàm logic từ MUX • Cách hiện thực LUT (Look-up table) - Sử dụng MUX để chọn một giá trị (hằng số) từ 1 LUT Ví dụ hàm XOR 39 Tổng hợp các hàm logic từ MUX • Giải pháp ở slide trước không hiệu quả vì phải sử dụng MUX 4-to-1 • Nhận xét: 40 Tổng hợp các hàm logic từ MUX • Ví dụ: Hiện thực mạch với bảng sự thật sau bằng một MUX và các cổng khác A B X 0 0 1 0 1 1 1 0 0 1 1 1 41 Tổng hợp các hàm logic từ MUX • XOR 3 ngõ vào có thể hiện thực bằng 2 MUX 2-to-1 42 Tổng hợp các hàm logic từ MUX • Ví dụ: Hiện thực mạch với bảng sự thật sau bằng một MUX và các cổng logic khác A B C X 0 0 0 1 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 - Với A là ngõ vào điều khiển - Với C là ngõ vào điều khiển 43 Biểu thức Shannon • Bất kì hàm Boolean f(w1,w2, , wn) có thể được viết dưới dạng: f(w1,w2, , wn) = 𝑤1*f(0,w2, ..., wn) + w1*f(1, w2, wn) 44 Biểu thức Shannon • Ví dụ 1: f(w1,w2, w3)= w1w2 + w1w3 + w2w3 • Phân tích hàm này theo biến w1: f(w1,w2, w3)= w1(w2 + w3) + 𝑤1(w2w3) f khi w1=1 f khi w1= 0 45 Biểu thức Shannon 46 Biểu thức Shannon • Ví dụ 2: Chọn x làm biến mở rộng 47 Biểu thức Shannon • Ví dụ 3: Chọn z làm biến mở rộng 48 Ví dụ • Dùng MUX 4-to-1 và các cổng luận lý cần thiết để hiện thực hàm sau: F (a, b, c, d) = SOP (1, 3, 5, 6, 8, 11, 15) • Yêu cầu: c và d là các ngõ vào điều khiển của MUX 4-ra-1 49 Ví dụ • Dùng MUX 4-to-1 và các cổng luận lý cần thiết để hiện thực hàm sau: F (a, b, c, d) = SOP (1, 3, 5, 6, 8, 11, 15) • Yêu cầu: b và c là các ngõ vào điều khiển của MUX 4-to-1 50 7. Parity Generator/ Checker 51 Cổng Exclusive OR và Exclusive NOR XOR: X Y F '' YXYXYX '')'( YXYXYX XOR: NAND 3 cấp XNOR: XOR: AND-OR Bảng sự thật 52 XOR and XNOR Symbols • Các biểu tượng tương đương của cổng XOR • Các biểu tượng tương đương của cổng XNOR Qui tắc tạo cổng XOR/XNOR tương đương: Lấy bù bất kì 2 trong 3 tín hiệu (cả input hoặc output) của cổng XOR/XNOR ban đầu. 53 Ứng dụng của XOR: Mạch Parity • Mạch Parity chẵn (EVEN): tổng số bit 1 trong chuỗi bit (kể cả bit parity) là số chẵn. – Parity bit = 1, nếu số bit 1 trong chuỗi bit (không kể parity) là số lẻ – Parity bit = 0, nếu số số 1 trong chuỗi bit (không kể parity) là số chẵn • Mạch Parity lẻ (ODD): tổng số bit 1 trong chuỗi bit (kể cả bit parity) là số lẻ. • Ví dụ: Mạch tạo Parity 4-bit Input Even Parity Odd Parity 0000 0 1 0001 1 0 1101 1 0 1111 0 1 1100 0 1 EVEN ODD ODD EVEN 54 Ứng dụng của XOR: Mạch tạo Parity Tree structure Daisy-Chain Structure EVEN EVEN 55 Ứng dụng của XOR: Mạch Parity Source: 56 Chip 74x280: tạo parity chẵn/lẽ từ dữ liệu 9-bit Chú ý: Chip 74x280 định nghĩa even/odd parity ngược lại với định nghĩa trong các slide trước => cẩn thận khi sử dụng chip này 57 Bộ tạo và kiểm tra Parity (Parity generator and checker) • Cổng XOR và XNOR rất hữu dụng trong các mạch với mục đích tạo (bộ phát) và kiểm tra (bộ nhận) parity bit 58 Ứng dụng của XOR: Mạch tạo Parity Source: 59 Ứng dụng cổng XOR: kiểm tra Parity Source: 60 8. Comparator 61 Mạch so sánh (Comperator) • Mạch so sánh 2 số – Xuất ra 1 nếu chúng bằng nhau – Xuất ra 0 nếu chúng khác nhau • Dựa trên cổng XOR, trả về 0 nếu ngõ vào giống nhau và 1 nếu chúng khác nhau • Dựa trên cổng XNOR, trả về 1 nếu ngõ vào giống nhau và 0 nếu chúng khác nhau 62 Mạch so sánh 1 bit a b gt eq lt 0 0 0 1 0 0 1 0 0 1 1 0 1 0 0 1 1 0 1 0 63 Mạch so sánh 4 bit a0 b3 a3 b2 a2 b1 a1 b0 eq 64 Mạch so sánh 4 bit a0 b3 a3 b2 a2 b1 a1 b0 gt 65 Mạch so sánh 4 bit lt 66 Mạch so sánh 4-bit • 74x85 là mạch so sánh tiêu chuẩn với những đặc tính sau: if (A>B) lt=0, eq=0, gt=1 if (A<B) lt=1, eq=0, gt=0 if (A=B) lt=l, eq=e, gt=g • Chý ý: 3 ngõ vào l, e và g được sử dụng khi ghép nối để tạo mạch so sánh với số bit nhiều hơn 4 4 B A g e l gt eq lt 67 Mạch so sánh 16 bit • Ghép 4 IC 74x85 để xây dựng một mạch so sánh 16 bit a[ 15:0 ] b[ 15:0 ] [15:12] 4 4 B A g e l gt eq lt 4 4 B A g e l gt eq lt [15:12] [11:8] [11:8] [7:4] 4 4 B A g e l gt eq lt 4 4 B A g e l gt eq lt 0 1 0 [7:4] [3:0] [3:0] gt eq lt Final results of comparison 68 Mạch so sánh 16 bit • Mạch sẽ đầu tiên so sánh 4 bit cao nhất ở 2 ngõ vào • Trong bước đầu này: – ‘a’ nhỏ hơn ‘b’ nếu 4 MSB nhỏ hơn – ‘a’ lớn hơn ‘b’ nếu 4 MSB lớn hơn – Nếu 4 MSB của 2 số bằng nhau, kết quả của phép so sánh sẽ chờ cho kết quả so sánh ở vị trí các bit thấp hơn 69 Ví dụ • Thiết kế mạch tìm số lớn nhất, số nhỏ nhất trong 4 số 4-bit sử dụng mạch so sánh và MUXs 70 Any question?
File đính kèm:
 bai_giang_nhap_mon_mach_so_chuong_5_phan_2_mach_to_hop_cac_l.pdf
bai_giang_nhap_mon_mach_so_chuong_5_phan_2_mach_to_hop_cac_l.pdf

