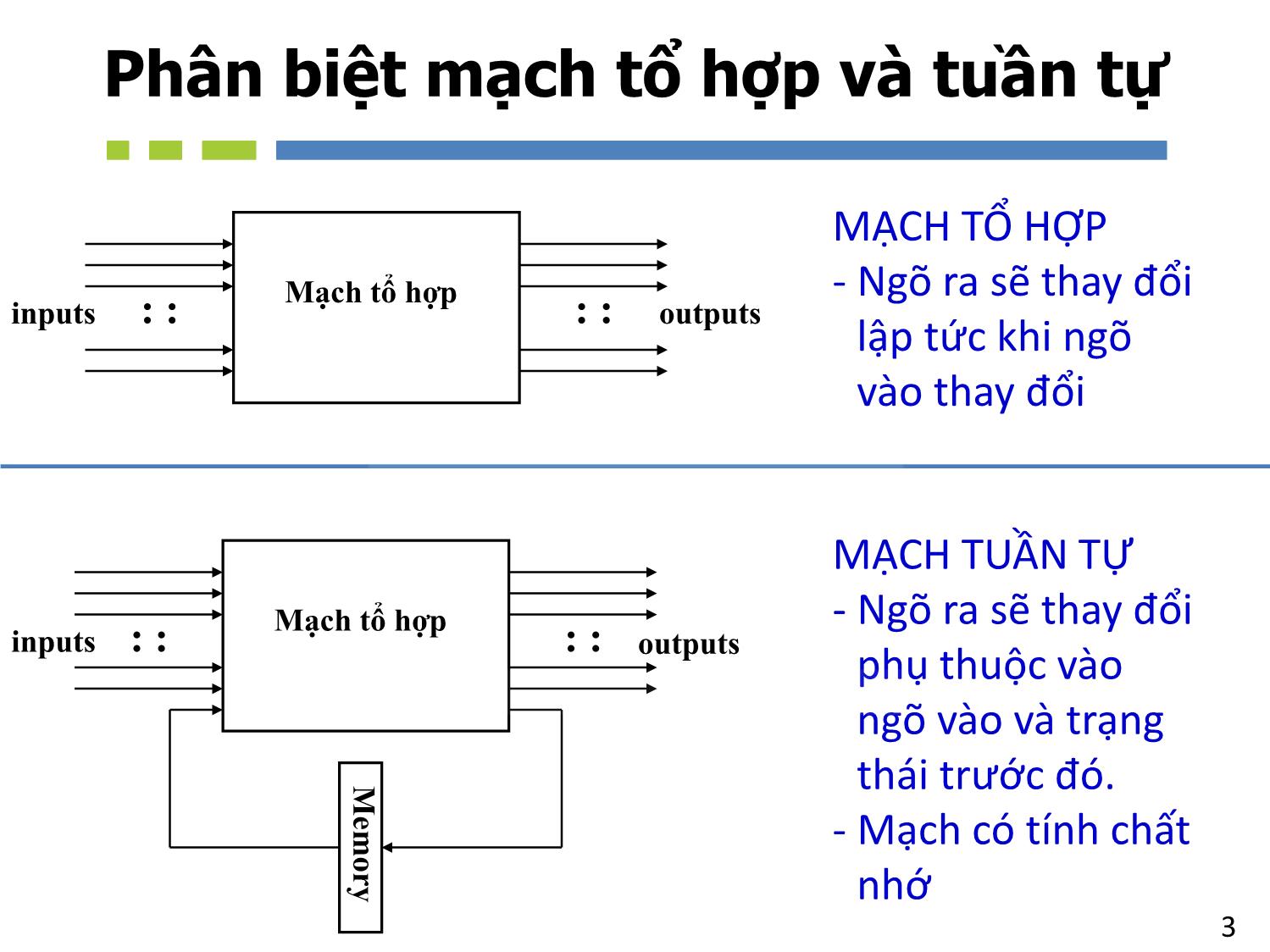
Bài giảng Nhập môn mạch số - Chương 5, Phần 1: Mạch tổ hợp. Mạch tính toán số học - Hồ Ngọc Diễm
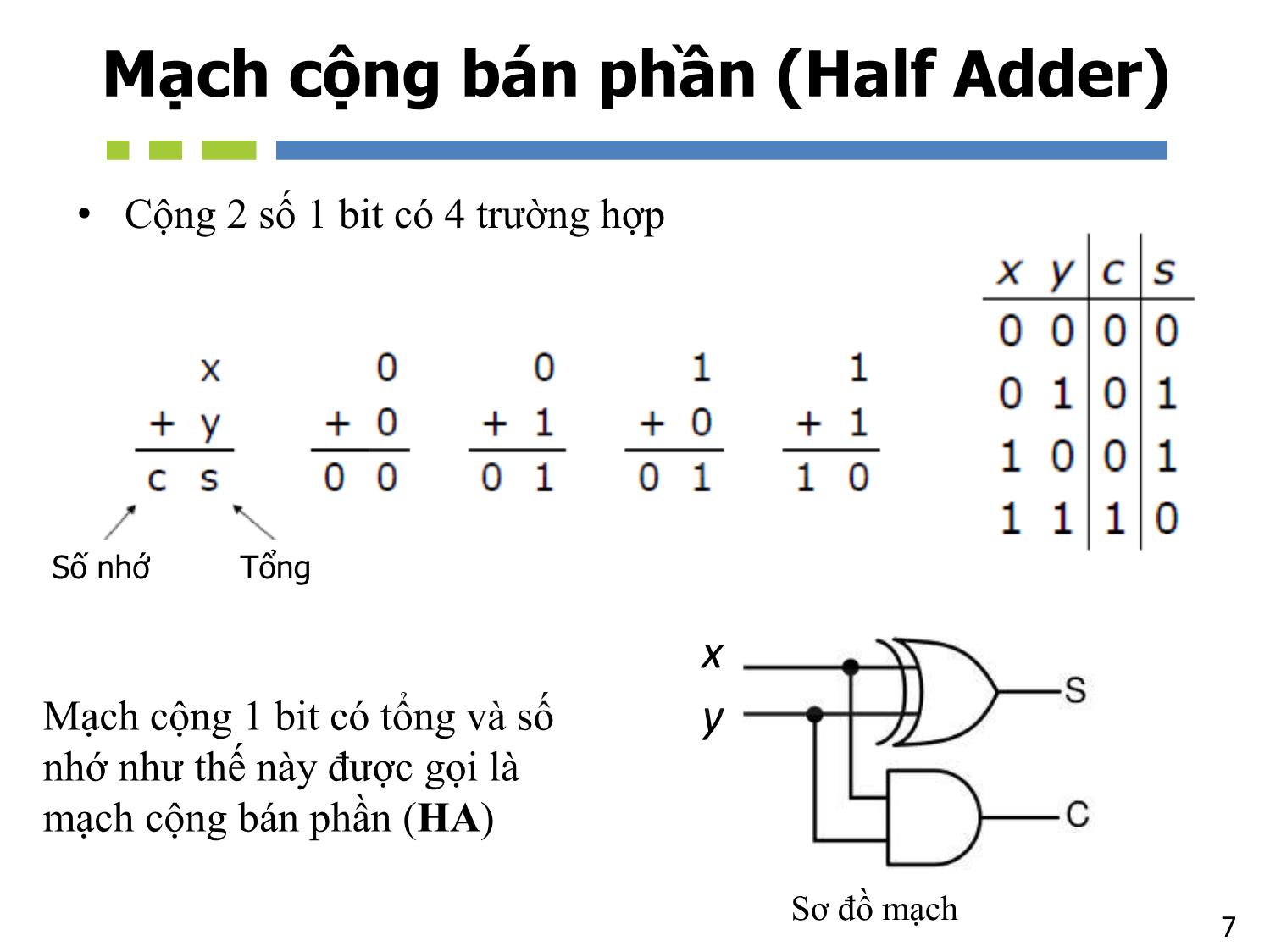
Mạch cộng bán phần (Half Adder)
Mạch cộng 1 bit có tổng và số
nhớ như thế này được gọi là
mạch cộng bán phần (HA)
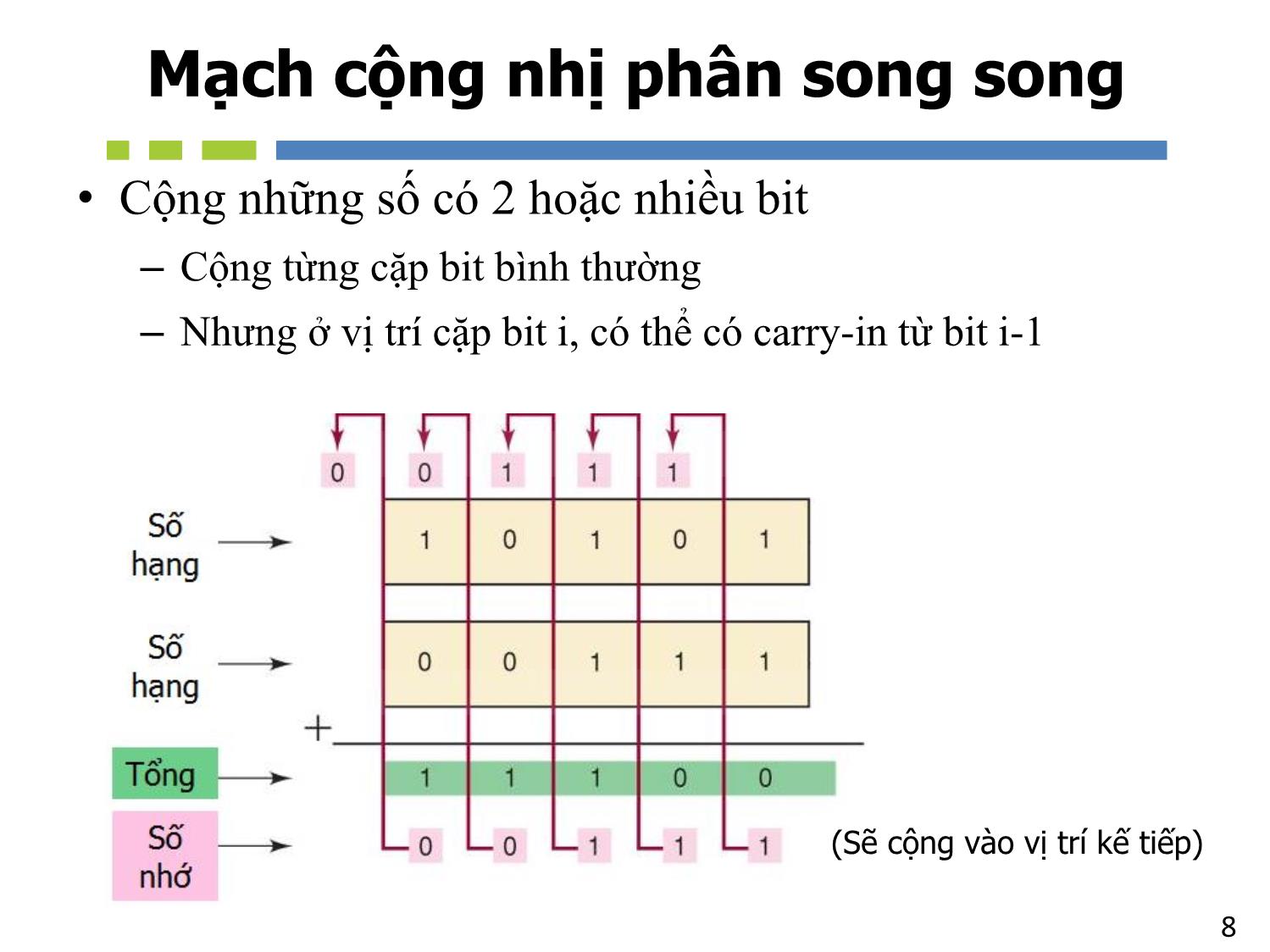
Mạch cộng nhị phân song song
• Cộng những số có 2 hoặc nhiều bit
– Cộng từng cặp bit bình thường
– Nhưng ở vị trí cặp bit i, có thể có carry-in từ bit i-1
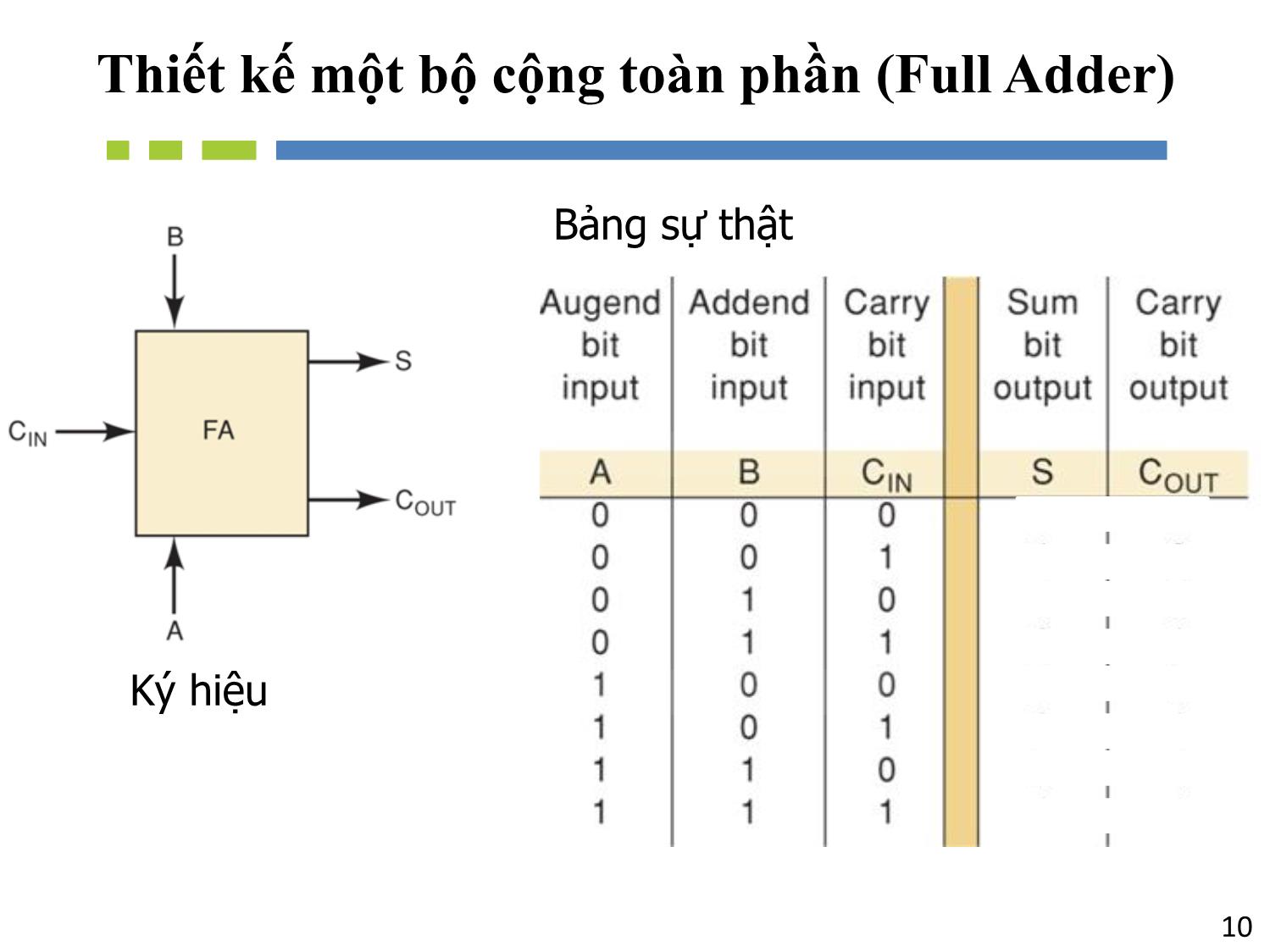
Thiết kế một bộ cộng toàn phần (Full Adder)
Bộ cộng toàn phần (FA)
– 3 ngõ vào (2 ngõ vào cho 2 số 1-bit cần tính tổng,
và 1 ngõ vào cho số nhớ đầu vào (carry-in))
– 2 ngõ ra (1 ngõ ra cho tổng và 1 cho số nhớ đầu
ra (carry-out))

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6
Trang 7
Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Nhập môn mạch số - Chương 5, Phần 1: Mạch tổ hợp. Mạch tính toán số học - Hồ Ngọc Diễm", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Nhập môn mạch số - Chương 5, Phần 1: Mạch tổ hợp. Mạch tính toán số học - Hồ Ngọc Diễm

1Chương 5 – phần 1 NHẬP MÔN MẠCH SỐ Mạch tổ hợp: Mạch tính toán số học 2Tổng quan Chương này sẽ học về: - Một số mạch logic tổ hợp thông dụng - Thiết kế các mạch logic tổ hợp phức tạp sử dụng các mạch logic tổ hợp thông dụng 3Phân biệt mạch tổ hợp và tuần tự Mạch tổ hợp : : : :inputs outputs Mạch tổ hợp : :inputs outputs: : M e m o ry MẠCH TỔ HỢP - Ngõ ra sẽ thay đổi lập tức khi ngõ vào thay đổi MẠCH TUẦN TỰ - Ngõ ra sẽ thay đổi phụ thuộc vào ngõ vào và trạng thái trước đó. - Mạch có tính chất nhớ 4Nội dung 1. Mạch cộng (Carry Ripple (CR) Adder) 2. Mạch cộng nhìn trước số nhớ - (Carry Look-Ahead (CLA) Adder) 3. Mạch cộng/ mạch trừ 4. Đơn vị tính toán luận lý (Arithmetic Logic Unit) 5. Mạch giải mã (Decoder)/ Mạch mã hoá (Encoder) 6. Mạch dồn kênh (Multiplexer)/ Mạch chia kênh (Demultiplexer) 7. Mạch tạo Parity/ Mạch kiểm tra Parity 8. Mạch so sánh (Comparator) 5Nội dung 1. Mạch cộng (Carry Ripple (CR) Adder) 2. Mạch cộng nhìn trước số nhớ - (Carry Look-Ahead (CLA) Adder) 3. Mạch cộng/ mạch trừ 4. Đơn vị tính toán luận lý (Arithmetic Logic Unit) 5. Mạch giải mã (Decoder)/ Mạch mã hoá (Encoder) 6. Mạch dồn kênh (Multiplexer)/ Mạch chia kênh (Demultiplexer) 7. Mạch tạo Parity/ Mạch kiểm tra Parity 8. Mạch so sánh (Comparator) 61. Mạch cộng Carry Ripple (CR) 7• Cộng 2 số 1 bit có 4 trường hợp Mạch cộng 1 bit có tổng và số nhớ như thế này được gọi là mạch cộng bán phần (HA) Mạch cộng bán phần (Half Adder) Sơ đồ mạch x y TổngSố nhớ 8Mạch cộng nhị phân song song • Cộng những số có 2 hoặc nhiều bit – Cộng từng cặp bit bình thường – Nhưng ở vị trí cặp bit i, có thể có carry-in từ bit i-1 (Sẽ cộng vào vị trí kế tiếp) 9Thiết kế một bộ cộng toàn phần (Full Adder) Bộ cộng toàn phần (FA) – 3 ngõ vào (2 ngõ vào cho 2 số 1-bit cần tính tổng, và 1 ngõ vào cho số nhớ đầu vào (carry-in)) – 2 ngõ ra (1 ngõ ra cho tổng và 1 cho số nhớ đầu ra (carry-out)) 10 Thiết kế một bộ cộng toàn phần (Full Adder) Bảng sự thật Ký hiệu 11 Thiết kế một bộ cộng toàn phần (Full Adder) i i i iS x y c 1i i i i i i ic x y x c y c 1i OUTc c i INc c Bảng sự thật 12 Thiết kế một bộ cộng toàn phần (Full Adder) Sơ đồ mạch Ký hiệu Ký hiệu khác i i i iS x y c 1i i i i i i ic x y x c y c 1i OUTc c i INc c 13 Thiết kế một bộ cộng toàn phần (Full Adder) i i i iS x y c 1 ( )i i i i i ic x y c x y • Sử dụng lại HA Sơ đồ mạch FA sử dụng lại HA Sơ đồ mạch HA x y Sơ đồ mạch 14 Mạch cộng Carry Ripple (CR) • Sơ đồ biểu diễn mạch cộng 4 bit song song sử dụng full adder 15 Mạch cộng Carry Ripple • Mạch FA bắt đầu với việc cộng các cặp bit từ LSB đến MSB – Nếu carry xuất hiện ở vị trí bit i, nó được cộng thêm vào phép cộng ở vị trí bit thứ i+1 • Việc kết hợp như vậy thường được gọi là mạch cộng Carry-Ripple – vì carry được “ripple” từ FA này sang các FA kế tiếp – Tốc độ phép cộng bị giới hạn bởi quá trình truyền số nhớ 16 Mạch cộng Carry Ripple • Mỗi FA có một khoảng trễ (delay), giả sử là Δt • Độ trễ phụ thuộc vào số lượng bit – Carry-out ở FA đầu tiên C1 có được sau Δt – Carry-out ở FA đầu tiên C2 có được sau 2Δt => Cn được tính toán sau nΔt Mô hình carry look ahead (CLA) thường được sử dụng để cải thiện tốc độ 17 2. Mạch cộng nhìn trước số nhớ Carry Look-Ahead (CLA) Adder 18 Hiệu năng • Tốc độ của mạch bị giới hạn bởi độ trễ lớn nhất dọc theo đường nối trong mạch – Độ trễ lớn nhất được gọi là critical-path-delay – Đường nối gây ra độ trễ đó gọi là critical path 19 Carry Look-Ahead Adder (CLA) • Cải thiện tốc độ mạch cộng bằng cách – Tại mỗi tầng (stage), ta sẽ xác định nhanh giá trị carry-in ở tầng cộng trước đó sẽ có giá trị 0 hay 1 giảm critical-path-delay 20 • Hàm xác định carry-out ở lần cộng thứ i ci+1= xiyi + xici + yici = xiyi + (xi + yi)ci • Đặt gi = xiyi và pi = xi + yi => ci+1= gi + pici gi = 1 khi cả xi và yi đều bằng 1, không quan tâm ci g được gọi là hàm generate, vì carry-out luôn được generate ra khi g=1 pi = 1 khi xi = 1 hoặc yi = 1; carry-out = ci p được gọi là hàm propagate, vì carry-in = 1 được propagate (truyền) ở tầng cộng thứ i Carry Look-Ahead Adder (CLA) 21 • Xác định carry-out của mạch cộng n bit cn =gn-1 + pn-1cn-1 Mà cn-1=gn-2 + pn-2cn-2 cn=gn-1 + pn-1(gn-2 + pn-2cn-2) • Tiếp tục khai triển đến lần cộng đầu tiên cn=gn-1+pn-1gn-2+pn-1pn-2gn-3++pn-1pn-2.p1g0+pn-1pn-2.p1p0c0 Carry Look-Ahead Adder (CLA) cn=gn-1 + pn-1gn-2 + pn-1pn-2cn-2 22 Carry Look-Ahead Adder (CLA) Số nhớ đầu vào c0 được truyền qua tất cả các lần cộng Số nhớ sinh ra ở lần cộng thứ 1 và được truyền qua các lần cộng còn lại Số nhớ sinh ra ở lần cộng thứ n-3 và được truyền qua các lần cộng còn lại Số nhớ sinh ra ở lần cộng thứ n-2 và được truyền qua các lần cộng còn lại Số nhớ sinh ra ở lần cộng cuối cùng 23 • Ví dụ: Trường hợp cộng 4 bit C1 = G0 + P0.C0 C2 = G1 + P1.G0 + P1.P0.C0 C3 = G2 + P2.G1 + P2.P1.G0 + P2.P1.P0.C0 C4 = G3 + P3.G2 + P3.P2.G1 + P3P2.P1.G0 + P3P2.P1.P0.C0 Carry Look-Ahead Adder (CLA) 24 Mạch cộng Carry Ripple - critical path Tổng quát, độ trễ 2n+1 cổng đối với mạch cộng Carry Ripple n-bit Độ trễ 3 cổng đối với C1 Độ trễ 5 cổng đối với C2 25 Mạch cộng CLA - critical path C1 = G0 + P0.C0 C2 = G1 + P1.G0 + P1.P0.C0 Độ trễ 3 cổng đối với C1 Độ trễ 3 cổng đối với C2 Độ trễ 3 cổng đối với Cn Độ trễ tổng cộng cho mạch cộng CLA n-bit là độ trễ 4 cổng - gi, pi: độ trễ 1 cổng - Ci: độ trễ 2 cổng - Độ trễ 1 cộng còn lại là do tính tổng s 26 Mạch cộng CLA Cấu trúc của một tầng của mạch cộng CLA 27 Giới hạn của mạch cộng CLA • Biểu thức tính carry trong mạch cộng CLA cn=gn-1+pn-1gn-2+pn-1pn-2gn-3++pn-1pn-2.p1g0+pn-1pn-2.p1p0c0 CLA là giải pháp tốc độ cao (2 level AND-OR) • Vấn đề Fan-in có thể hạn chế tốc độ của mạch cộng CLA • Độ phức tạp tăng lên nhanh chóng khi n lớn 28 3 Adder/ Subtractor 29 Mạch cộng/ trừ • X,Y là 2 số không dấu n-bit Phép trừ: D = X - Y = X + (-Y) = X+ (Bù 2 của Y) = X+ (Bù 1 của Y) + 1 = X+ Y’+ 1 Phép cộng: S = X + Y 30 Mạch trừ • Mạch cộng Carry Ripple có thể được dùng để xây dựng mạch trừ Carry Ripple bằng cách đảo Y và đặt số nhớ đầu tiên là 1 31 Tràn (Arithmetic Overflow) • Overflow là khi kết quả của phép toán vượt quá số bit biểu diễn phần giá trị – n bit biểu diễn được số từ -2n-1 đến +2n-1-1 – Overflow luôn luôn cho ra 1 kết quả sai => Mạch để xác định có overflow hay không 32 Ví dụ về arithmetic overflow • Với số 4 bit, 3 bit giá trị và 1 bit dấu • Overflow không xuất hiện khi cộng 2 số trái dấu O O 33 Arithmetic overflow • Overflow có thể phát hiện được (từ ví dụ ở slide trước) • Mạch cộng/ trừ có thể bổ sung mạch kiểm tra overflow với 1 cổng XOR • Với n bit Overflow = cn-1 cn 34 Ví dụ • Thiết kế một mạch cộng/ trừ với 2 ngõ điều khiển ADD và SUB – ADD = 1: mạch cộng 2 số trong 2 thanh ghi A và B – SUB = 1: mạch thực hiện phép trừ số B-A Chú ý: Trong một lúc chỉ một trong hai ngõ ADD, SUB bằng 1 35 Ví dụ 36 4 Arithmetic Logic Unit (ALU) 37 ALU • ALUs có thể thực thi nhiều toán tử và hàm logic khác nhau – Các toán tử và hàm được xác định bởi một mã ngõ vào Inputs S2 S1 S0 Function 0 0 0 F = 0000 0 0 1 F = B – A – 1 + Cin 0 1 0 F = A – B – 1 + Cin 0 1 1 F = A + B + Cin 1 0 0 F = A B 1 0 1 F = A + B 1 1 0 F = A * B 1 1 1 F =1 11 38 Any question?
File đính kèm:
 bai_giang_nhap_mon_mach_so_chuong_5_phan_1_mach_to_hop_mach.pdf
bai_giang_nhap_mon_mach_so_chuong_5_phan_1_mach_to_hop_mach.pdf

