Bài giảng Nhập môn mạch số - Chương 3: Đại số Boolean và các cổng Logic - Hồ Ngọc Diễm

1CHƯƠNG 3
NHẬP MÔN MẠCH SỐ
Đại Số Boolean và Các Cổng Logic
2Tổng quan
Chương này sẽ học về:
- Đại số Boolean: với đặc điểm là chỉ thực hiện trên 
hai giá trị/trạng thái 0(OFF) và 1(ON) nên rất phù 
hợp với việc biểu diễn và tính toán trong các mạch 
logic Số
- Các cổng logic cơ bản, từ đó có thể xây dựng nên 
các mạch logic hoặc các hệ thống số phức tạp trong 
những chương sau.
3NỘI DUNG
• Cổng Logic cơ bản AND, OR, NOT
– Mạch Logic => Biểu thức Đại Số
– Biểu thức Đại Số => Mạch Logic 
• Cổng Logic NAND và NOR
• Đại số Boolean
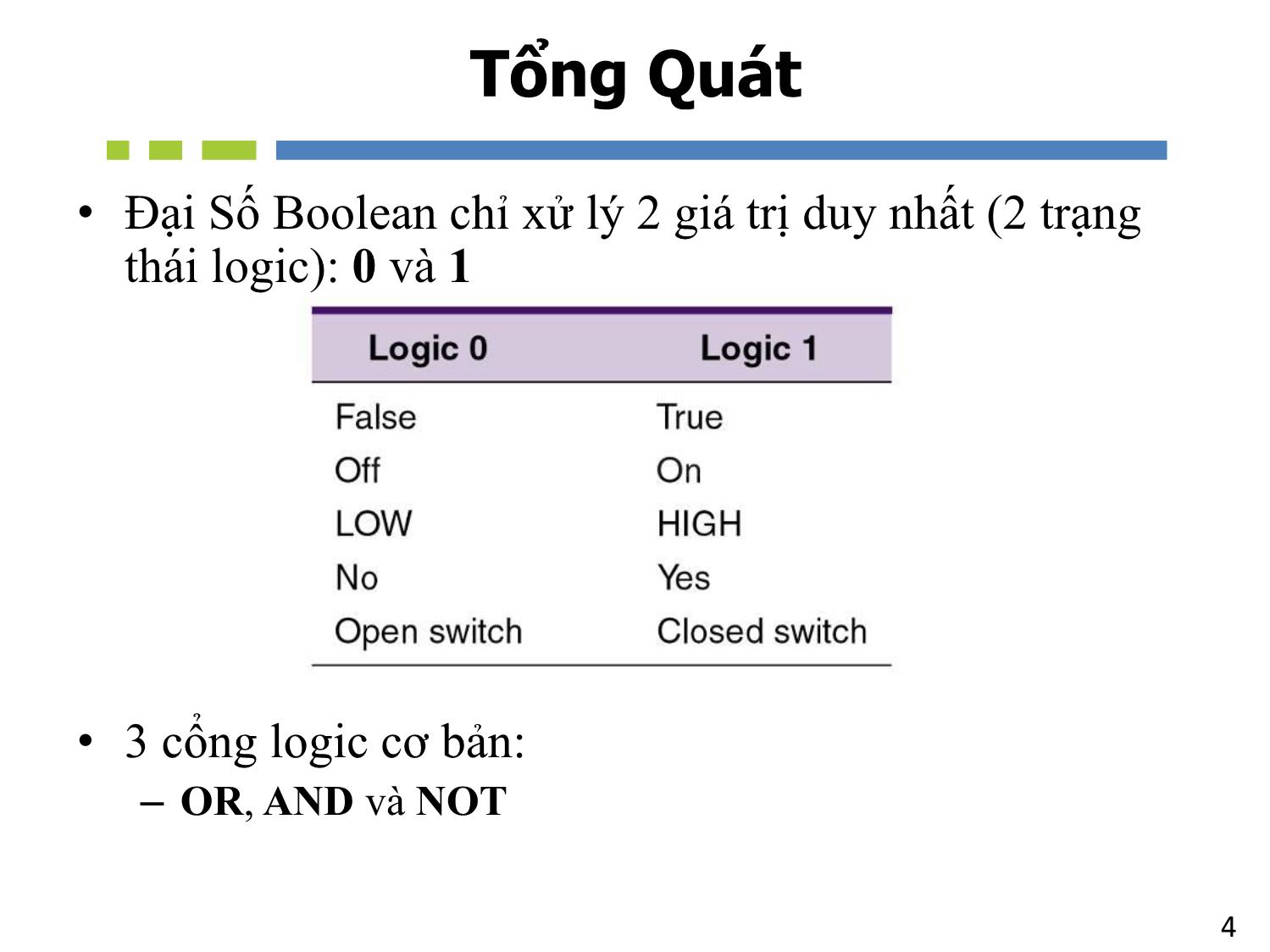
4Tổng Quát
• Đại Số Boolean chỉ xử lý 2 giá trị duy nhất (2 trạng
thái logic): 0 và 1
• 3 cổng logic cơ bản:
– OR, AND và NOT
5Cổng Logic Cơ Bản
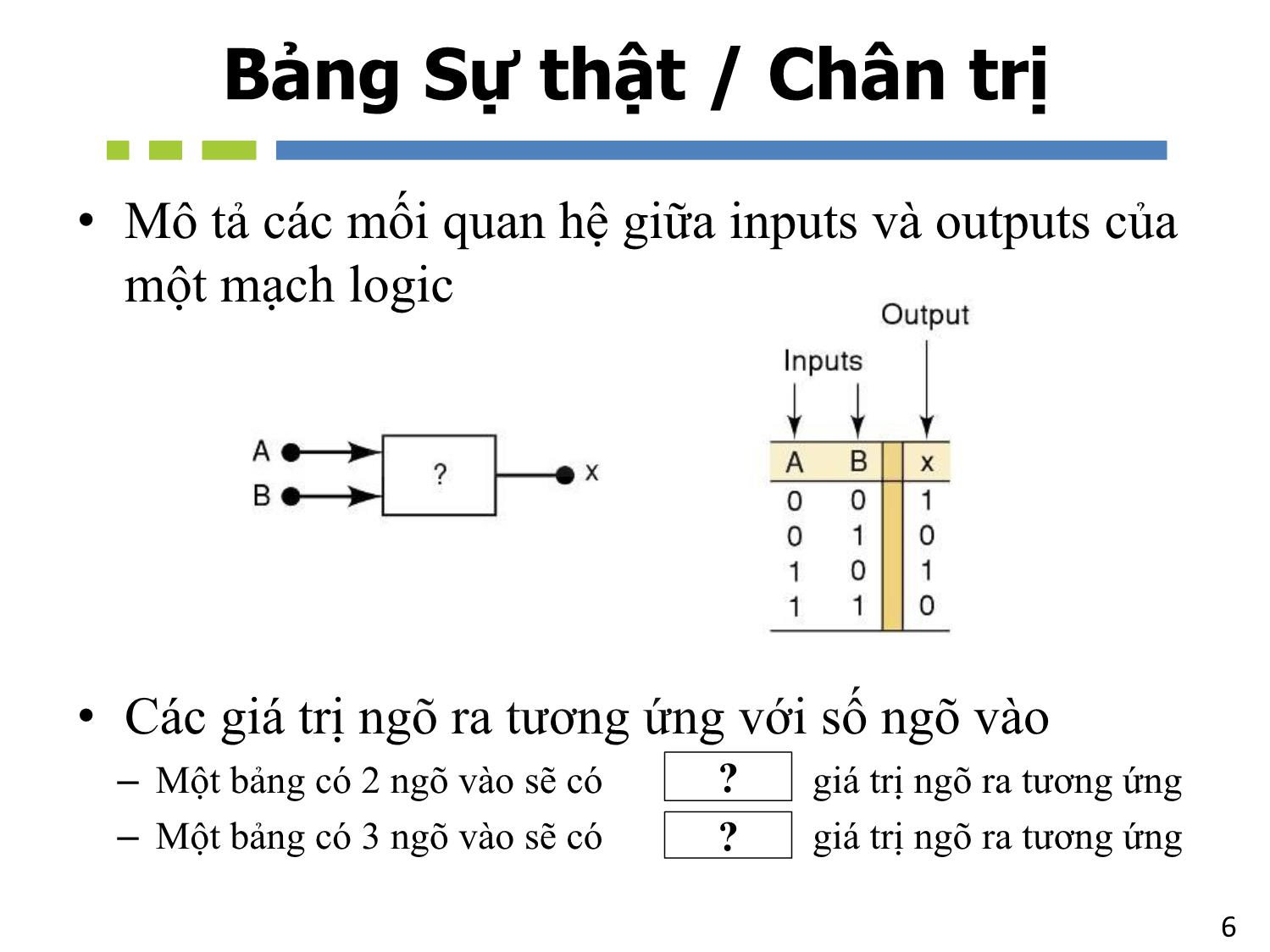
6Bảng Sự thật / Chân trị
• Mô tả các mối quan hệ giữa inputs và outputs của
một mạch logic
• Các giá trị ngõ ra tương ứng với số ngõ vào
– Một bảng có 2 ngõ vào sẽ có 22 = 4 giá trị ngõ ra tương ứng
– Một bảng có 3 ngõ vào sẽ có 23 = 8 giá trị ngõ ra tương ứng
?
?
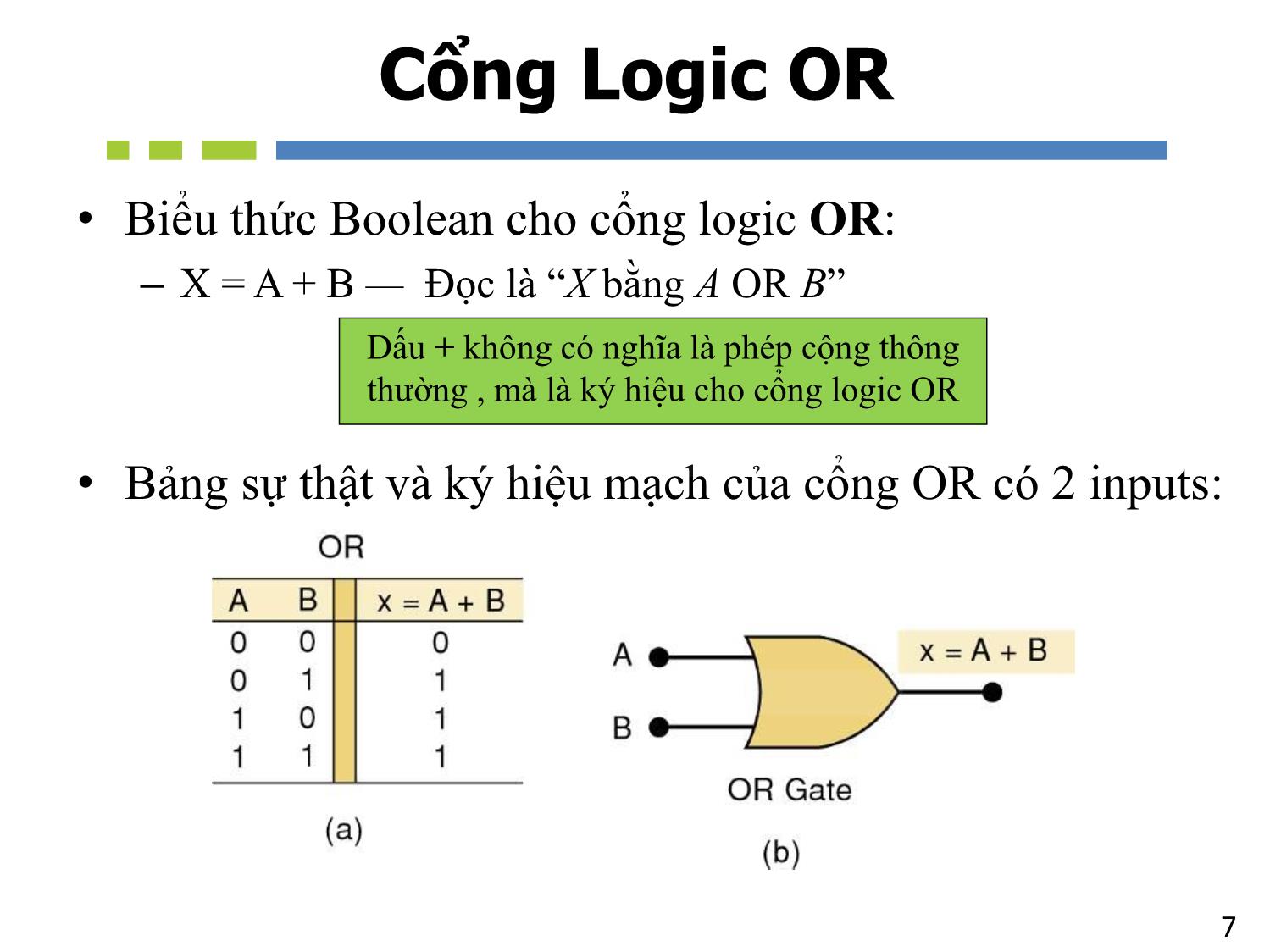
7Cổng Logic OR
• Biểu thức Boolean cho cổng logic OR:
– X = A + B — Đọc là “X bằng A OR B”
• Bảng sự thật và ký hiệu mạch của cổng OR có 2 inputs:
Dấu + không có nghĩa là phép cộng thông
thường , mà là ký hiệu cho cổng logic OR
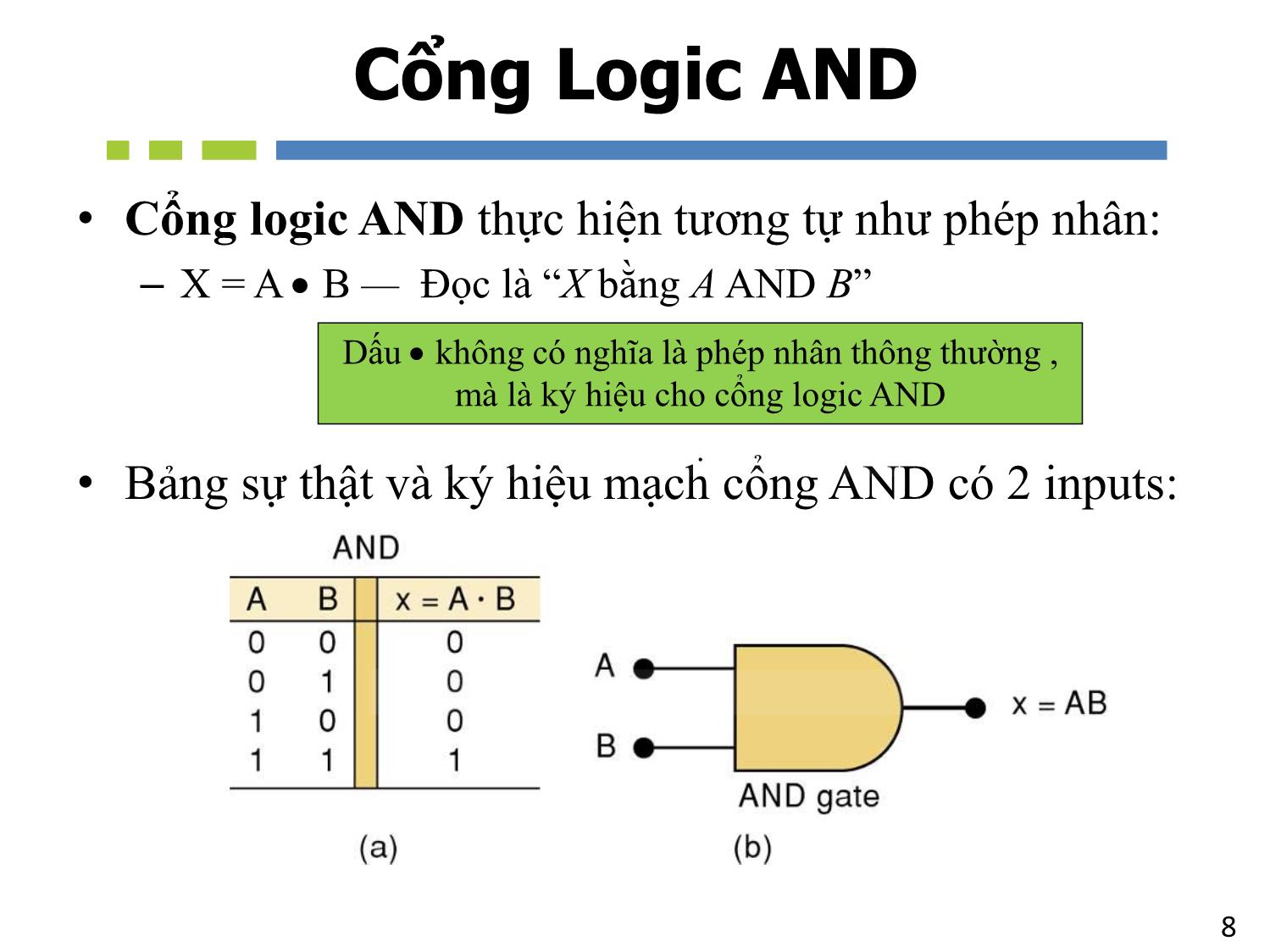
8Cổng Logic AND
• Cổng logic AND thực hiện tương tự như phép nhân:
– X = A B — Đọc là “X bằng A AND B”
• Bảng sự thật và ký hiệu mạch cổng AND có 2 inputs:
Dấu không có nghĩa là phép nhân thông thường , 
mà là ký hiệu cho cổng logic AND
.
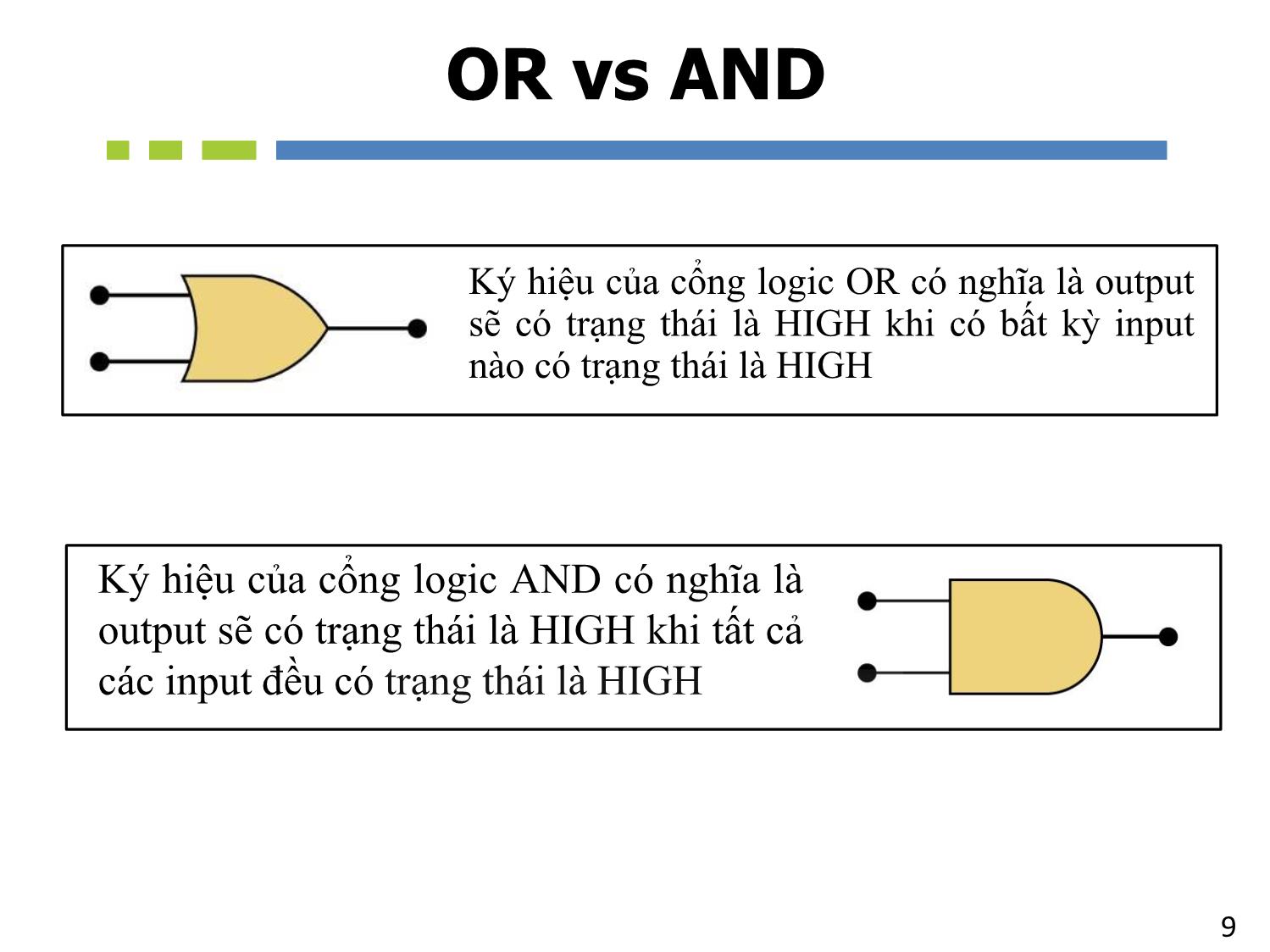
9OR vs AND
Ký hiệu của cổng logic OR có nghĩa là output
sẽ có trạng thái là HIGH khi có bất kỳ input
nào có trạng thái là HIGH
Ký hiệu của cổng logic AND có nghĩa là
output sẽ có trạng thái là HIGH khi tất cả
các input đều có trạng thái là HIGH
10
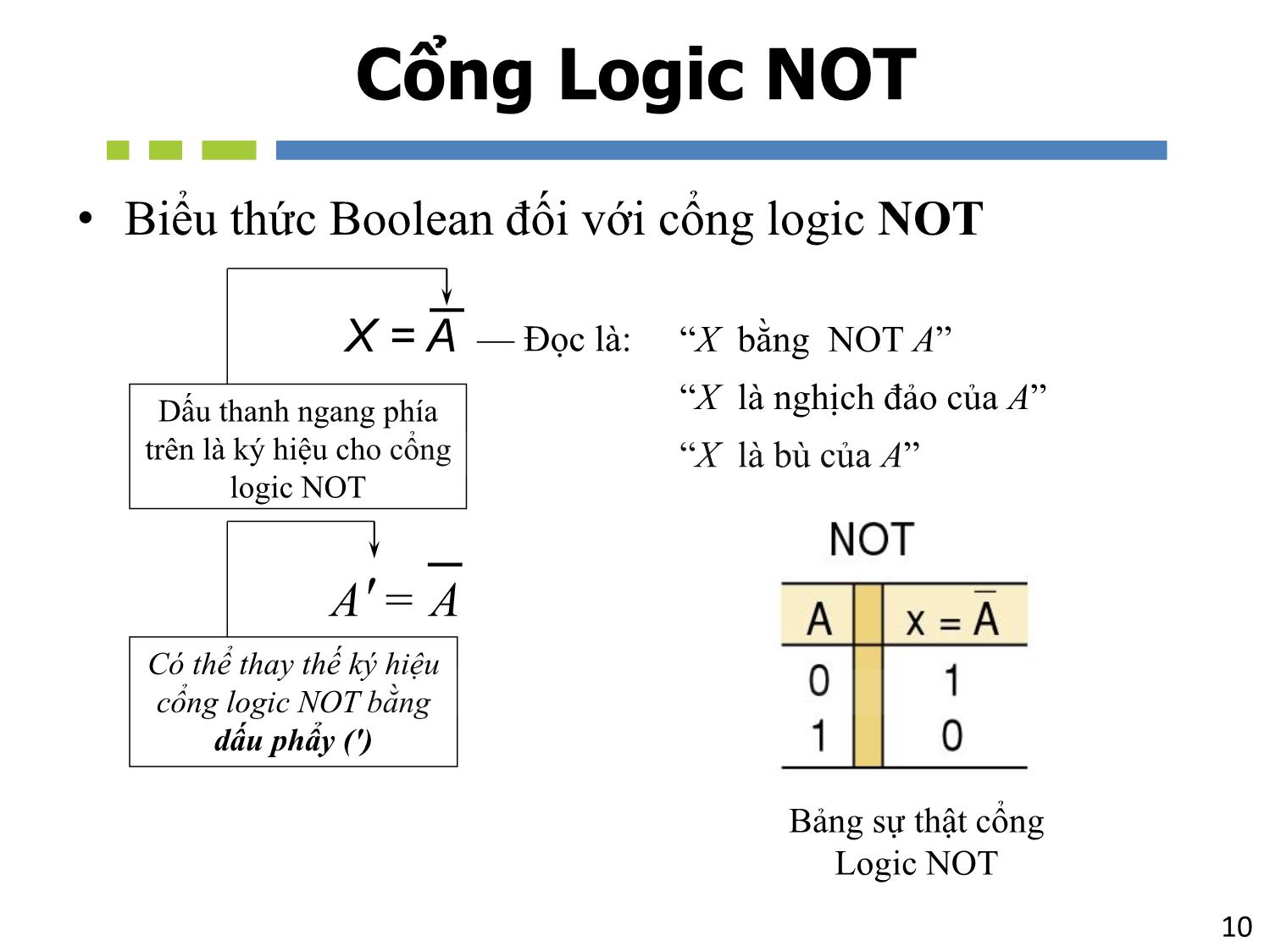
Cổng Logic NOT
• Biểu thức Boolean đối với cổng logic NOT
“X bằng NOT A”
“X là nghịch đảo của A”
“X là bù của A”
— Đọc là:X = A
A' = A
Dấu thanh ngang phía
trên là ký hiệu cho cổng
logic NOT
Có thể thay thế ký hiệu
cổng logic NOT bằng
dấu phẩy (')
Bảng sự thật cổng
Logic NOT
11
Cổng Logic NOT
• Cổng logic NOT có thể gọi chung là cổng INVERTER
Cổng logic này luôn luôn chỉ có duy nhất 1 
input, và trạng thái của output sẽ đối nghịch
với trạng thái của input
Dấu bù/đảo ngược
12
Bất cứ khi nào có: input = 0, output = 1, và ngược lại
Cổng Logic NOT
Cổng INVERTER nghịch đảo (lấy bù) tín hiệu ngõ vào tại
tất cả các thời điểm để tạo ra tín hiệu ngõ ra tương ứng
13
Cổng Logic Cơ Bản
Ba cổng logic Boolean cơ bản có thể mô tả
được bất kỳ mạch logic nào
14
Mạch Logic => Biểu thức đại số
15
Mô tả mạch logic đại số
• Nếu một biểu thức có chứa cả hai cổng Logic AND
và OR, thì cổng logic AND sẽ được thực hiện trước :
• Trừ khi có một dấu ngoặc trong biểu thức
16
Input A qua một inverter sẽ có output là A
Mô tả mạch logic đại số
17
Ví Dụ
18
Đánh giá OUTPUT của mạch logic
• Ex: X = ABC(D + E) + FG
Quy tắc đánh giá một biểu thức Boolean theo trình tự sau:
 Tính giá trị ngõ ra của các cổng đảo có một thành phần
 Tính giá trị biểu thức trong dấu ngoặc đơn
 Tính giá trị biểu thức cổng AND trước biểu thức cổng OR 
(nếu biểu thức cổng OR không có dấu ngoặc đơn)
 Nếu cả một biểu thức có thanh ngang trên đầu, thực hiện các
phép tính bên trong biểu thức trước, và sau đó đảo ngược kết
quả lại
19
Đánh giá OUTPUT của mạch logic
• Cách tốt nhất để phân tích một mạch gồm có nhiều
cổng logic khác nhau là sử dụng bảng sự thật
– Cho phép chúng ta có thể phân tích một cổng hoặc một
tổ hợp các cổng logic có trong mạch cùng một lúc
– Cho phép chúng ta dễ dàng kiểm tra lại hoạt động của
mạch logic một cách chính xác nhất
– Bảng sự thật giúp ích trong việc phát hiện và xử lý lỗi
hay sự cố xuất hiện trong mạch logic
20
• Đánh giá outputs của mạch logic sau:
Đánh giá OUTPUT của mạch logic
21
Đánh giá OUTPUT của mạch logic
• Bước 1: Liệt kê tất cả các inputs có trong mạch logic tổ hợp
• Bước 2: Tạo ra một cột trong bảng sự thật cho mỗi tín hiệu 
trung gian (node)
Node u đã được điền vào như là kết quả của
phần bù của tín hiệu input A
22
Đánh giá OUTPUT của mạch logic
• Bước 3: điền vào các giá trị tín hiệu của cột node v
v =AB — Node v sẽ có giá trị HIGH
Khi A (node u) là HIGH và B là HIGH
23
Đánh giá OUTPUT của mạch logic
• Bước 4: Dự đoán trước giá trị tín hiệu của node w là
outputs của cổng logic BC
Node w là HIGH khi và chỉ khi B là HIGH và cả C là HIGH
24
Đánh giá OUTPUT của mạch logic
• Bước cuối cùng: kết hợp một cách logic 2 cột v và w
để dự đoán cho output x
Từ biểu thức x = v + w, thì x sẽ là HIGH khi v OR w là HIGH
25
Đánh giá OUTPUT của mạch logic
• Ví dụ:
26
Biểu thức đại số=> Mạch Logic
27
Thiết kế mạch logic từ biểu thức Boolean
- Biểu thức x = A.B.C có thể được thực hiện bởi 
một cổng AND có 3 ngõ vào.
- Một mạch logic có biểu thức x = A + B sẽ sử
dụng 1 cổng logic OR gồm có 2 inputs, trong đó
có 1 input sẽ có cổng INVERTER kèm theo.
28
Ví Dụ
y = AC + BC+ ABC Vẽ sơ đồ mạch logic với output 
như sau:
29
• Mỗi ngõ vào của cổng OR là ngõ ra của các cổng
AND trước đó
Ví Dụ (tt)
30
Cổng Logic NOR và NAND
31
Cổng Logic NOR
• NOR = NOT OR
– X = A + B
Dấu bù/đảo ngược
32
Cổng Logic NAND
• NAND = NOT AND
– X = A B
Dấu bù/ đảo 
ngược
33
Ví Dụ NAND/NOR
X = AB (C +D)
Vẽ sơ đồ mạch thực hiện 
biểu thức logic:
- Chỉ sử dụng cổng logic OR, AND, NOT
- Chỉ sử dụng cổng logic NOR và NAND
Lưu ý: Nếu đề không yêu cầu cổng logic sử dụng có bao nhiêu ngõ vào,
thì người thiết kế có thể chọn cổng logic có bao nhiêu ngõ vào cũng được.
34
Đại Số Boolean
35
Đại Số Boolean
• Máy tính kỹ thuật số là tổng hợp các mạch logic được thực
hiện dựa trên những biểu thức của đại số Boolean (biểu thức
Boolean)
• Biểu thức Boolean càng đơn giản, thì mạch thực hiện càng nhỏ 
 giá thành rẻ hơn, tiêu tốn ít công suất hơn, và thực hiện 
nhanh hơn mạch phức tạp
• Dựa vào các định luật Boolean sẽ giúp ta đơn giản được các 
biểu thức Boolean về dạng đơn giản nhất
36
Định Luật Boolean I
Định Luật 2 nếu một cổng AND-2 có 1
ngõ vào bằng 1, thì ngõ ra sẽ bằng giá trị
với ngõ vào còn lại.
Định Luật 1 nếu một cổng AND-2 có
1 ngõ vào bằng 0, thì ngõ ra sẽ bằng 0
bất kể giá trị ngõ vào còn lại.
Định Luật 3 xét từng trường hợp
Nếu x = 0, thì 0 • 0 = 0
Nếu x = 1, thì 1 • 1 = 1
Do đó, x • x = x
Định Luật 4 có thể chứng minh bằng
cách tương tự
37
Định Luật 5 nếu một cổng OR-2 có 1
ngõ vào bằng 0, thì ngõ ra sẽ bằng giá
trị với ngõ vào còn lại
Định Luật Boolean II
Định Luật 6
Định Luật 8 có thể chứng minh một cách
tương tự
Định Luật 7 có thể chứng minh bằng
cách kiểm tra cả hai giá trị của x:
0 + 0 = 0 and 1 + 1 = 1
nếu một cổng OR-2 có 1 ngõ vào bằng 1, thì 
ngõ ra sẽ bằng 1 bất kể giá trị ngõ vào còn lại
38
Định Luật Boolean III
(13c) x + yz = (x + y)(x + z)
PHÉP GIAO HOÁN
PHÉP LiÊN KẾT / KẾT HỢP
PHÉP PHÂN PHỐI
39
Định Luật Boolean IV
• Định Luật Đa Biến
• Định Luật (14) và (15) không gặp trong đại số thông 
thường. 
40
Định Luật Boolean V
Tính ñoái ngaãu (Duality):
Hai bieåu thöùc ñöôïc goïi laø ñoái ngaãu cuûa nhau khi ta
thay pheùp toaùn AND baèng OR, pheùp toaùn OR baèng
AND, 0 thaønh 1 vaø 1 thaønh 0
Ví Dụ
41
Định Luật DeMorgan’s
• Định Luật DeMorgan’s là phương pháp cực kỳ hữu
ích trong việc đơn giản hóa các biểu thức trong đó
một tích hay tổng của các biến được đảo ngược
42
Định Luật DeMorgan’s
• Mạch tương đương với ngụ ý của Định Luật (16)
Mạch logic khác tương 
đương với hàm NOR
43
Định Luật DeMorgan’s
• Mạch tương đương với ngụ ý của Định Luật (17)
Mạch logic khác tương 
đương với hàm NAND
44
Ví Dụ #1
• Áp dụng các định luật Boolean để đơn giản biểu thức
sau đây:
45
Ví Dụ #2
• Use DeMorgan theorem to simplify below
expressions
(i) (M + N)(M + N)
(ii) (A + C + D)
Áp dụng định luật DeMorgan để đơn giản các biểu thức
sau
46
Ví dụ #3
74LS00 chip
Chỉ sử dụng cổng NAND để thực hiện các cổng logic cơ bản 
(NOT, OR, AND)
47
Tính phổ biến của cổng NAND 
• Chỉ sử dụng cổng NAND để thực hiện 3 cổng logic 
cơ bản (AND, OR, NOT)
Có thể thực hiện được bất cứ biểu thức logic nào chỉ sử dụng
duy nhất 1 loại cổng logic NAND
48
Example #4
74LS02 chip
Chỉ sử dụng cổng NOR để thực hiện các cổng logic cơ bản 
(NOT, OR, AND)
49
Tính phổ biến của cổng NOR
• Chỉ sử dụng cổng NOR để thực hiện 3 cổng logic cơ 
bản (AND, OR, NOT)
Có thể thực hiện được bất cứ biểu thức logic nào chỉ sử dụng
duy nhất 1 loại cổng logic NOR
50
Danh sách chip IC thuộc họ 74LS
Source:
51
Biểu diễn cổng logic (mở rộng)
• Ý nghĩa của 2 loại cổng logic NAND
Tích cực mức cao
Tích cực mức thấp
Output là LOW khi
tất cả inputs là HIGH
Output là HIGH khi
có ít nhất 1 input có
trạng thái là LOW
Trạng thái thấp là 
trạng thái tích cực
Trạng thái cao là 
trạng thái tích cực
52
Biểu diễn cổng logic (mở rộng)
Để biến đổi một cổng logic cơ bản sang một cổng logic 
tương đương, phải thực hiện các bước sau:
– Chuyển đổi OR sang AND hoặc AND sang OR
– Nghịch đảo tất cả input và output trong cổng logic cơ bản
• Thêm ký hiệu dấu bù (bong bóng) tại ngõ vào/ngõ ra không có
• Xóa ký hiệu dấu bù (bong bóng) tại ngõ vào/ngõ ra có sẵn
53
Biểu diễn cổng logic (mở rộng)
Để biến đổi một cổng logic cơ bản sang một cổng logic 
tương đương, phải thực hiện các bước sau:
– Chuyển đổi OR sang AND hoặc AND sang OR
– Nghịch đảo tất cả input và output trong cổng logic cơ bản
• Thêm ký hiệu dấu bù (bong bóng) tại ngõ vào/ngõ ra không có
• Xóa ký hiệu dấu bù (bong bóng) tại ngõ vào/ngõ ra có sẵn
54
Inverter
Truth table
Timing 
diagram
Boolean 
algebra
AND gate
một cổng logic thực hiện việc đảo ngược/lấy bù 
ngõ vào của nó
một bảng chỉ ra giá trị ngõ vào và ngõ ra tương ứng
của một mạch logic
một giản đồ chỉ ra dạng sóng của các tín hiệu trong
mạch logic tại từng thời điểm
Phương pháp toán học cho mạch logic
Thuật ngữ kỹ thuật số
Với cổng AND có nhiều ngõ vào, ngõ ra sẽ là 1
nếu tất cả các ngõ vào đều là 1.
55
Thuật ngữ kỹ thuật số
OR gate
NAND gate
NOR gate
Exclusive-OR 
gate
Exclusive-NOR 
gate
Vôùi coång OR coù nhieàu ngoõ vaøo, 
ngoõ ra seõ laø 0 neáu taát caû caùc ngoõ vaøo ñeàu laø 0
Vôùi coång NAND coù nhieàu ngoõ vaøo, 
ngoõ ra seõ laø 0 neáu taát caû caùc ngoõ vaøo ñeàu laø 1
Vôùi coång NOR coù nhieàu ngoõ vaøo,
ngoõ ra seõ laø 1 neáu taát caû caùc ngoõ vaøo ñeàu laø 0
Vôùi coång XOR coù nhieàu ngoõ vaøo, ngoõ ra seõ laø 1
neáu toång soá bit 1 ôû caùc ngoõ vaøo laø soá leû
Vôùi coång XNOR coù nhieàu ngoõ vaøo, ngoõ ra seõ laø 1
neáu toång soá bit 1 ôû caùc ngoõ vaøo laø soá chaün