Bài giảng Nhập môn mạch số - Chương 2: Các dạng biểu diễn số - Hồ Ngọc Diễm

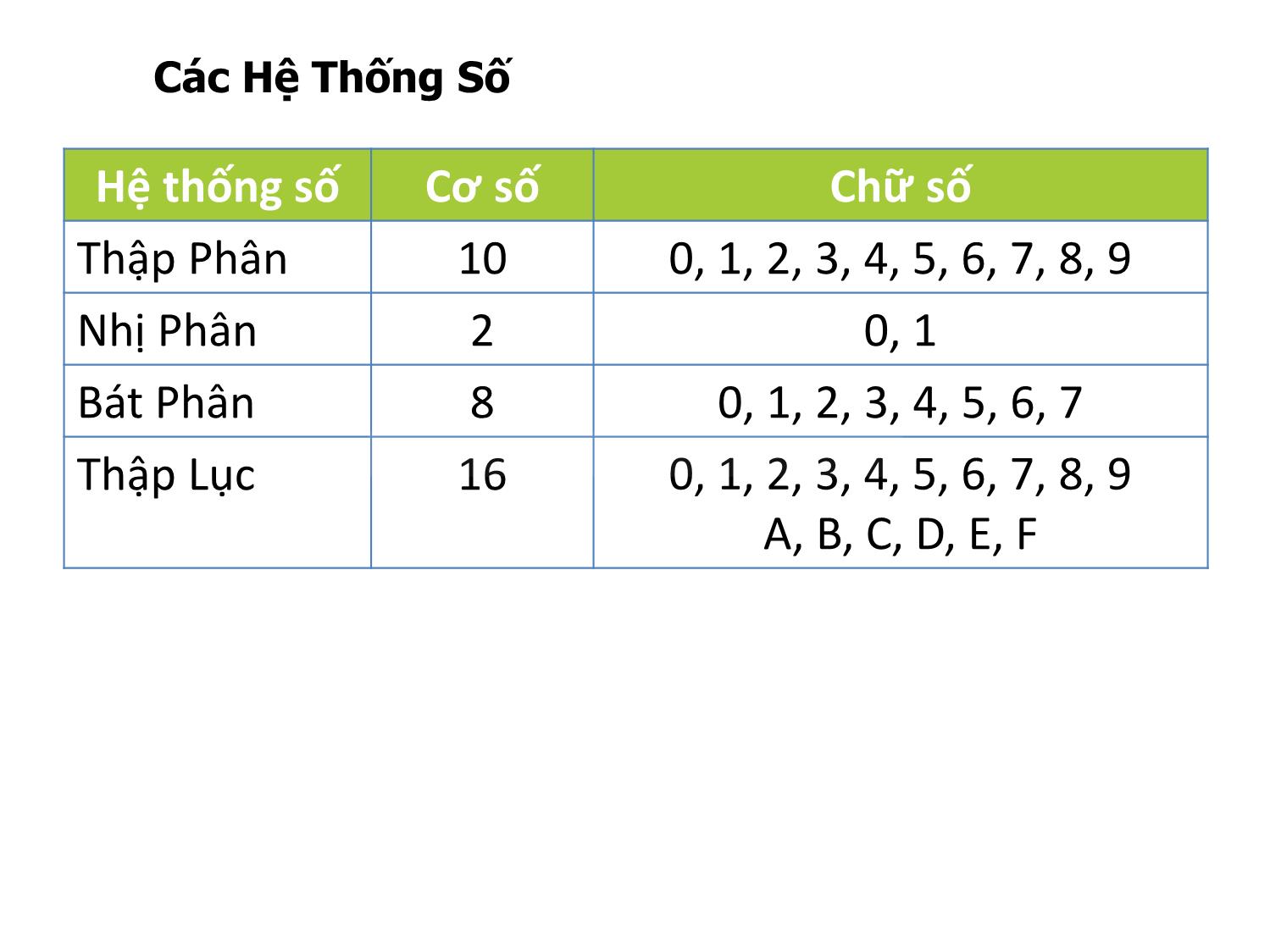
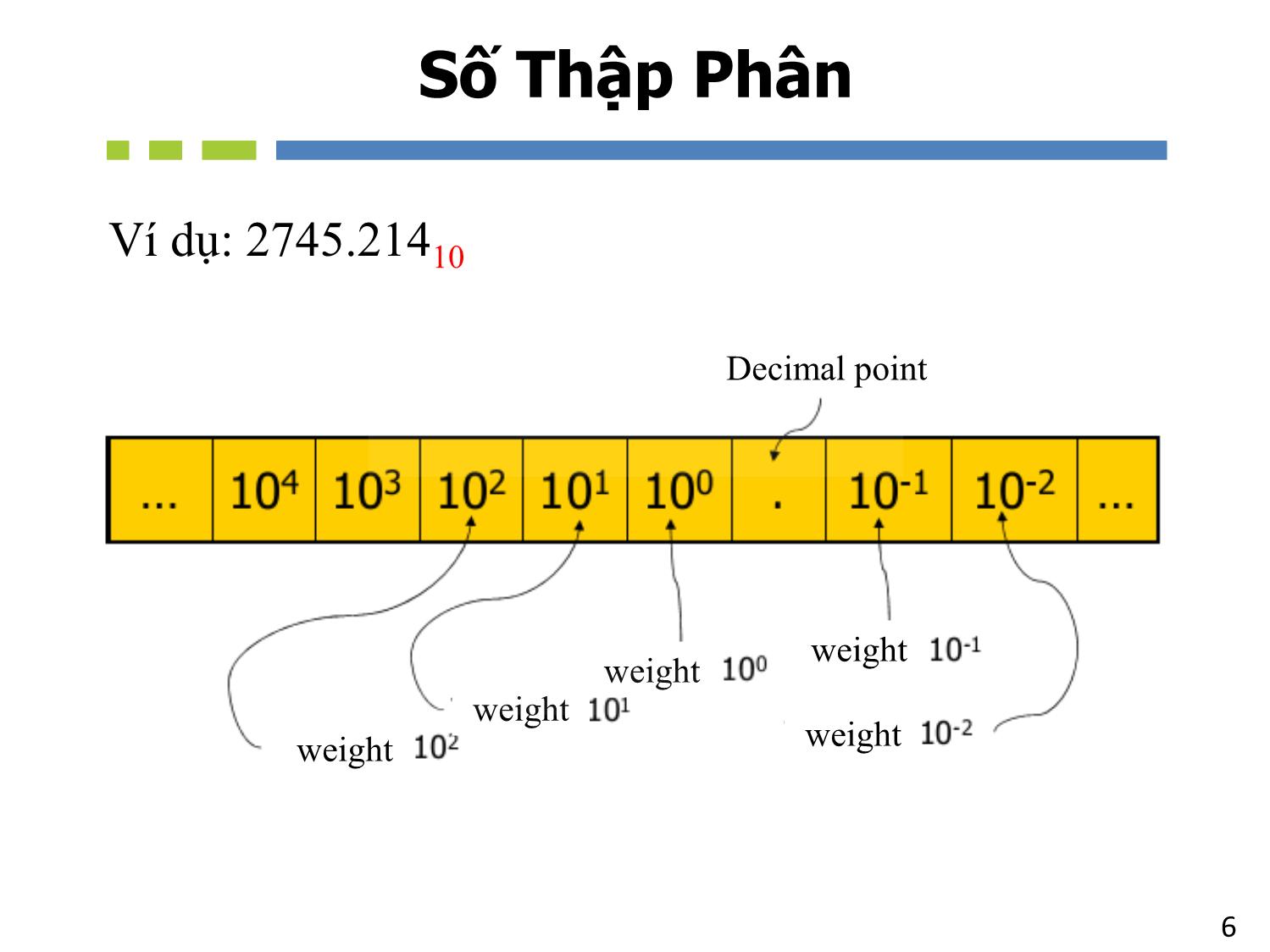
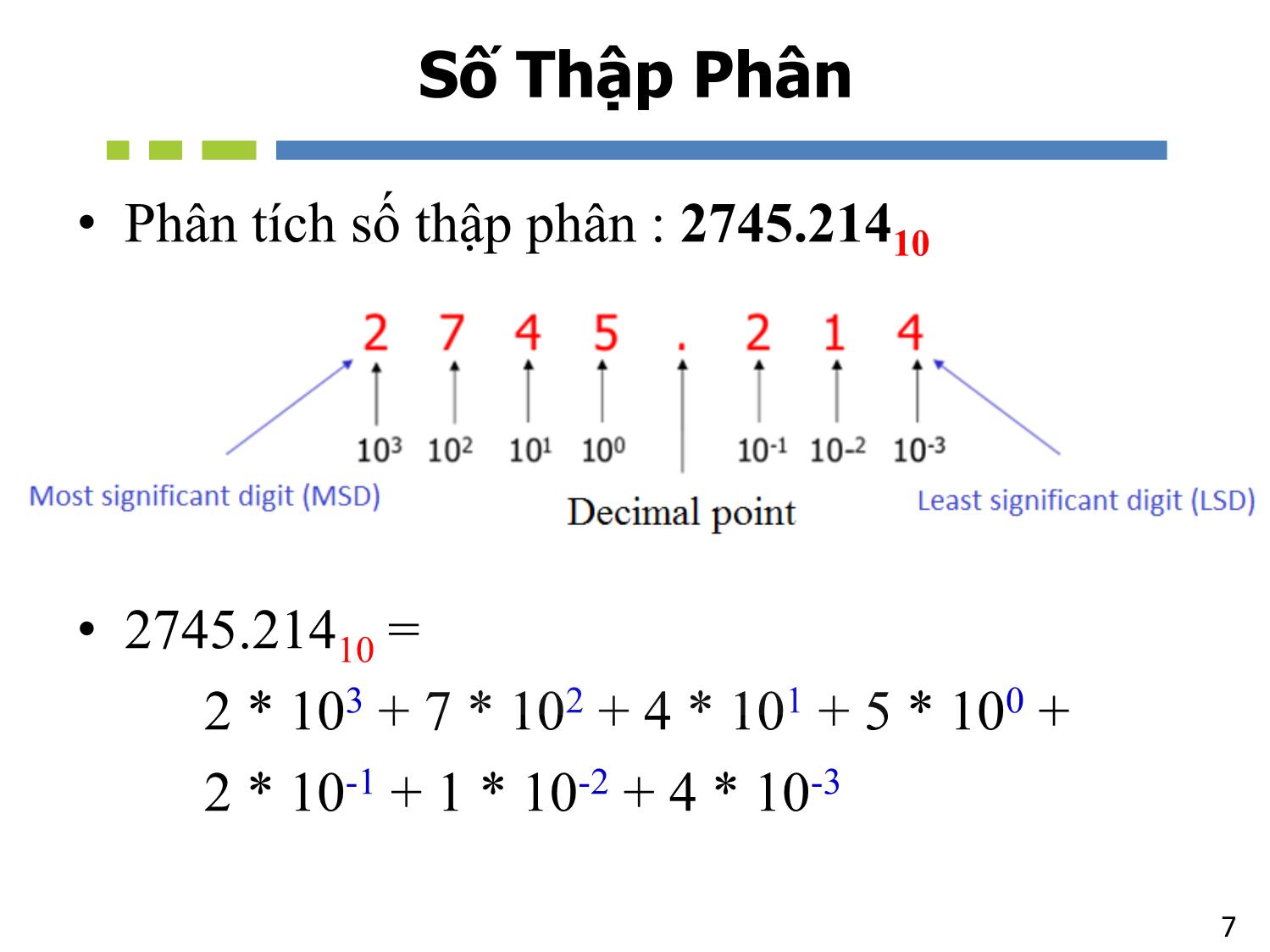
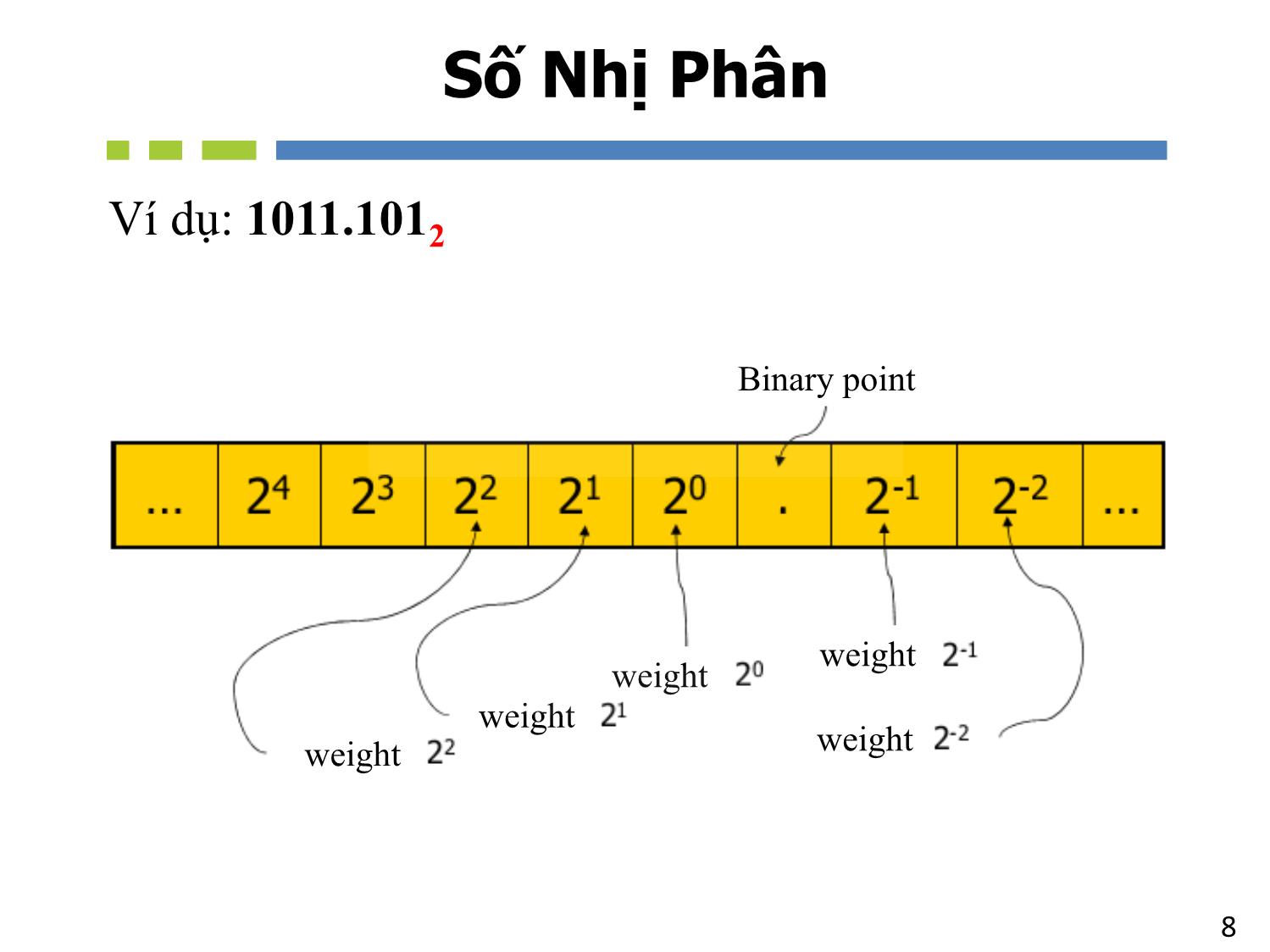
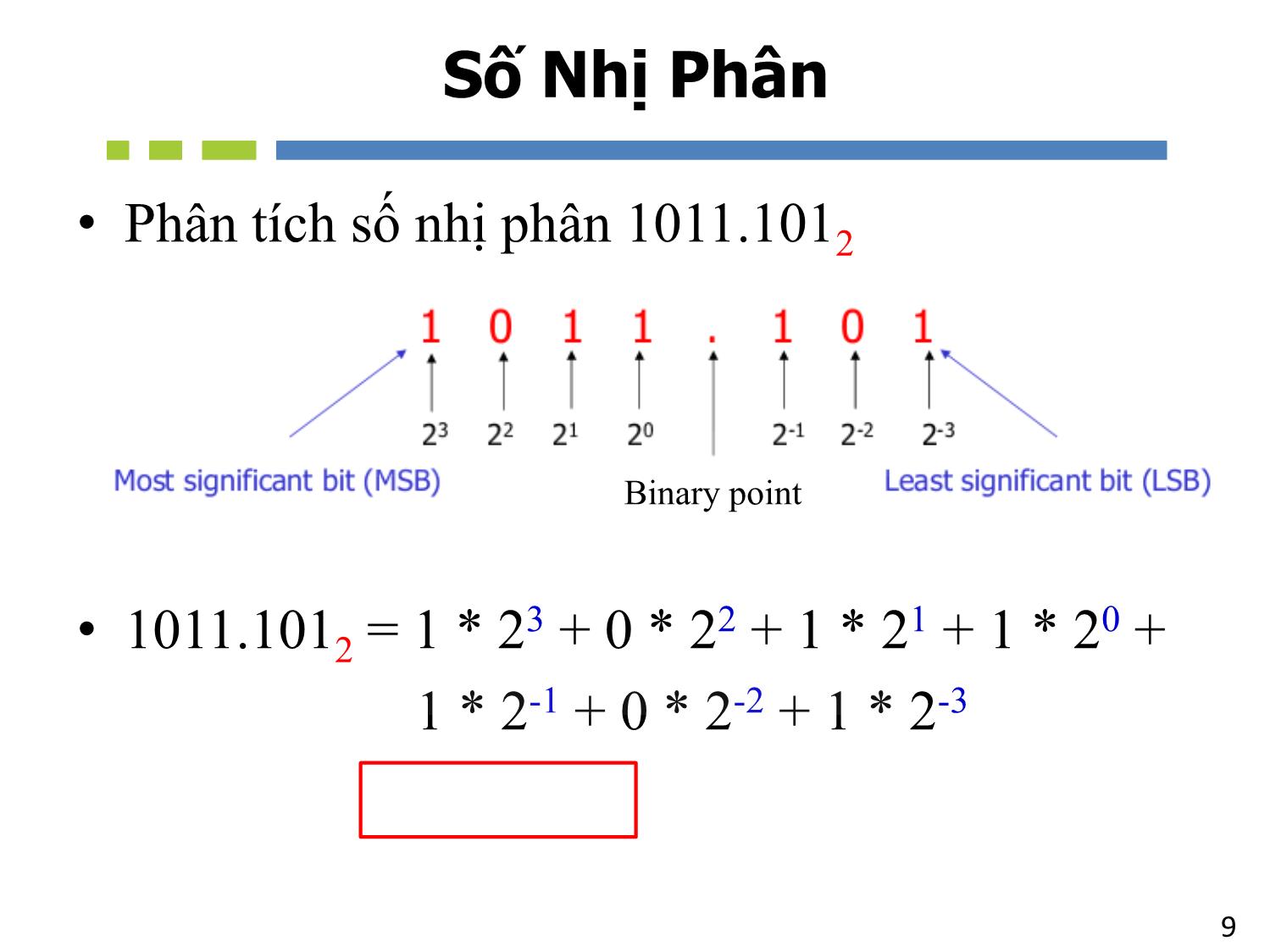
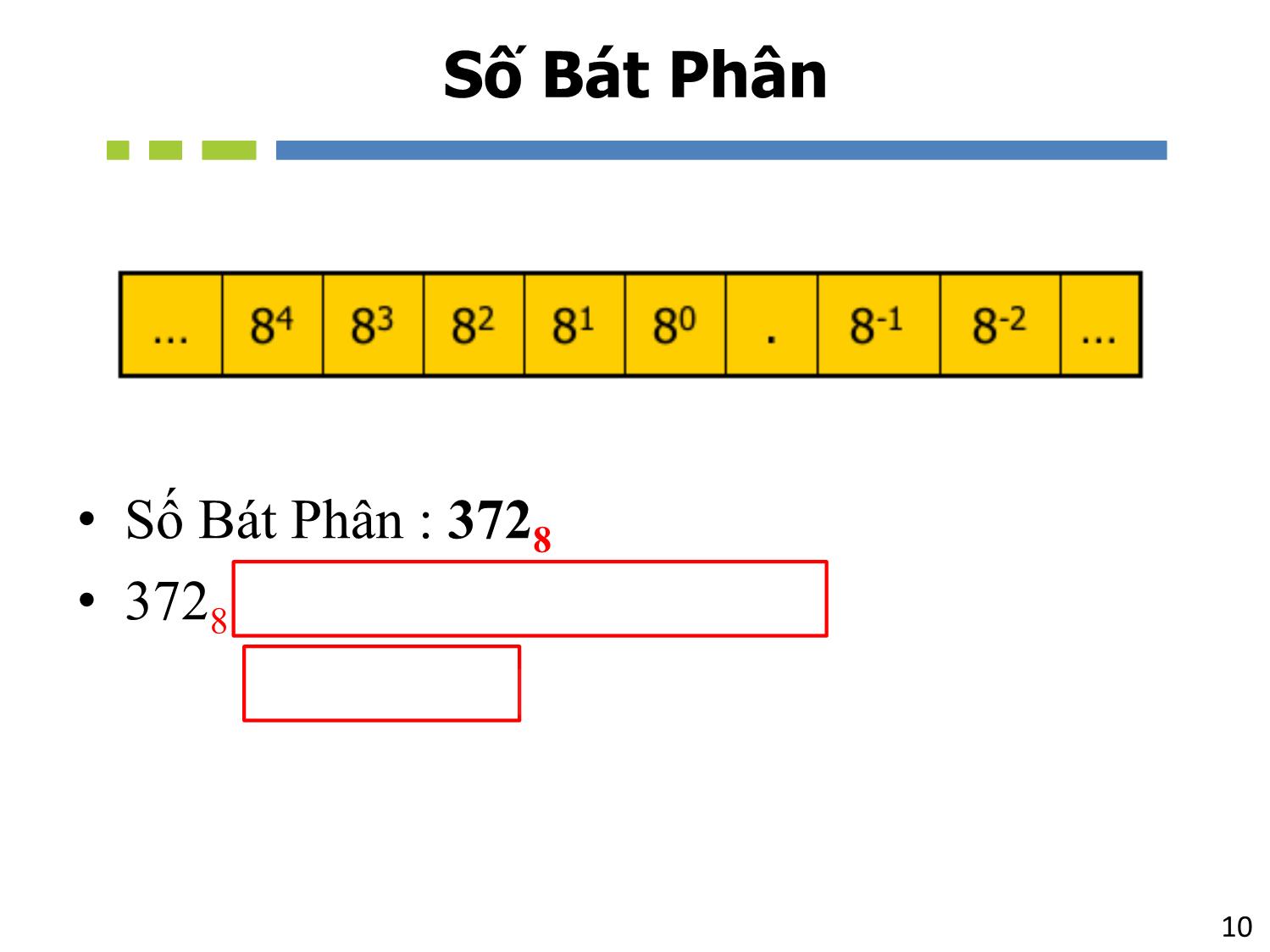
Chương 2
NHẬP MÔN MẠCH SỐ
Các Dạng Biểu Diễn Số
2Tổng quan
- Các hệ thống số/máy tính đều dùng hệ thống số nhị 
phân để biểu diễn và thao tác. Trong khi, hệ thống số 
thập phân được dùng rộng rãi và quen thuộc trong đời 
sống hằng ngày.
- Một số hệ thống số khác (bát phân, thập lục phân,) 
cũng được giới thiệu trong chương này giúp cho sự 
biểu diễn của hệ thống số nhị phân được dễ hiểu và 
tiện lợi với con người.
- Trình bày các kỹ thuật để chuyển đổi qua lại giữa các 
hệ thống số.
- Sự biểu diễn và thao tác với số có dấu trong các hệ 
thống số
3Nội Dung
1. Giới thiệu các hệ thống số
– Số Thập Phân
– Số Nhị Phân
– Số Thập Lục Phân
– Số Bát Phân
2. Chuyển đổi giữa các hệ thống số
3. Biểu diễn số nhị phân
4. Biểu diễn số có dấu
5. Biểu diễn các loại số khác
– Số dấu chấm động
– BCD
– ASCII
1. Giới thiệu các hệ thống số
• Số Thập Phân
• Số Nhị Phân
• Số Thập Lục Phân
• Số Bát Phân
Hệ thống số Cơ số Chữ số
Thập Phân 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Nhị Phân 2 0, 1
Bát Phân 8 0, 1, 2, 3, 4, 5, 6, 7
Thập Lục 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
A, B, C, D, E, F
Các Hệ Thống Số
6Số Thập Phân
weight
weight
weight
weight
weight
Decimal point
Ví dụ: 2745.21410
7Số Thập Phân
• Phân tích số thập phân : 2745.21410
• 2745.21410 = 
2 * 103 + 7 * 102 + 4 * 101 + 5 * 100 +
2 * 10-1 + 1 * 10-2 + 4 * 10-3
8Số Nhị Phân
weight
weight
weight
weight
weight
Binary point
Ví dụ: 1011.1012
9Số Nhị Phân
• Phân tích số nhị phân 1011.1012
• 1011.1012 = 1 * 2
3 + 0 * 22 + 1 * 21 + 1 * 20 +
1 * 2-1 + 0 * 2-2 + 1 * 2-3
= 11.62510
Binary point
10
Số Bát Phân
• Số Bát Phân : 3728
• 3728 = 3 * 8
2 + 7 * 81 + 2 * 80
= 25010
11
Số Thập Lục Phân
• Phân tích số thập lục phân : 3BA16
• 3BA16 = 3 * 16
2 + 11 * 161 + 10 * 160
= 95410
Chuyển đổi giữa các hệ thống số
13
Chuyển đổi sang số thập phân
• Nhân mỗi chữ số (digit) với trọng số (weight) 
14
Ví Dụ
• Biểu diễn 37028 sang số thập phân
• Biểu diễn 1A2F16 sang số thập phân
15
Số Thập Phân => Số Nhị Phân
• Chia số thập phân với 2 và sau đó viết ra phần dư còn lại
– Chia cho đến khi có thương số là 0.
• Phần số dư đầu tiên gọi là LSB (Bit có trọng số thấp nhất)
• Phần số dư cuối cùng gọi là MSB (Bit có trọng số cao nhất)
Decimal Binary
16
Ví dụ : 2510 => Số Nhị Phân
17
Số Thập Phân => Số Thập Lục Phân
Decimal Hexadecimal
• Chia số thập phân cho 16 và viết ra phần dư còn lại
– Chia cho đến khi có thương số là 0.
• Phần số dư đầu tiên gọi là LSD (Số có trọng số thấp nhất)
• Phần số dư cuối cùng gọi là MSD (Số có trọng số cao nhất)
18
Ví Dụ: 42310 => Thập Lục Phân
19
Thập Phân => Bát Phân
Decimal Octal
• Chia số thập phân cho 8 và viết ra phần dư còn lại
– Chia cho đến khi có thương số là 0.
• Phần số dư đầu tiên gọi là LSD (Số có trọng số thấp nhất)
• Phần số dư cuối cùng gọi là MSD (Số có trọng số lớn nhất)
20
Bát Phân => Nhị Phân
• Chuyển đổi lần lượt mỗi chữ số ở dạng Bát Phân sang 
nhóm 3 bits Nhị Phân
• VD:
BinaryOctal
Octal 0 1 2 3 4 5 6 7
Binary 000 001 010 011 100 101 110 111
8
2
21
Thập Lục Phân => Nhị Phân
• Chuyển đổi lần lượt mỗi chữ số ở dạng Thập Lục
Phân sang nhóm 4 bits Nhị Phân
• VD:
BinaryHexadecimal
Hex Bin
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
16
2
22
Nhị Phân => Bát Phân
• Nhóm 3 bits bắt đầu từ ngoài cùng bên phải của số
• Chuyển đổi mỗi nhóm trên sang dạng chữ số của Bát
Phân
• VD: 10110101112 => Bát Phân
13278
Binary Octal
23
Nhị Phân => Thập Lục Phân
• Nhóm 4 bits từ phía ngoài cùng bên phải của số
• Chuyển đổi mỗi nhóm trên sang 1 chữ số Thập Lục
• VD: 101011010101110011010102 => Thập Lục Phân
56AE6A16
Binary Hexadecimal
24
Bát Phân Thập Lục Phân
HexadecimalOctal
Binary
• Chuyển đổi thông qua trung gian là số Nhị Phân
25
Ví dụ: 1F0C16 => Bát Phân
Chuyển đổi từ Thập Lục Phân sang Nhị Phân
1F0C16 = 1_1111_0000_11002
Chuyển đổi từ Nhị Phân sang Bát Phân
1_111_100_001_1002 = 174148
26
Ví Dụ: 10768 => Thập Lục phân
Chuyển đổi từ Bát Phân sang Nhị Phân
10768 = 1_000_111_1102
Chuyển đổi từ Nhị Phân sang Thập Lục Phân
10_0011_11102 = 23E16
27
Ví Dụ
• Thực hiện phép chuyển đổi giữa các hệ thống số
Decimal Binary Octal Hexadecimal
35
1101101
712
1AF
28
Phân Số
• Số Thập Phân => Số Nhị Phân
29
Ví dụ: 189.02310 => Số Nhị Phân
30
Ví Dụ
• Thực hiện phép chuyển đổi giữa các hệ thống số
Decimal Binary Octal Hexadecimal
29.8
110.1101
3.07
C.82
Các phép tính số nhị phân
• Phép Cộng
• Phép Nhân
• Phép Trừ
32
Phép Cộng
• Cộng 2 số nhị phân 1-bit
A B A + B
0
0
1
1
0
1
0
1
0
1
1
10
33
Phép Cộng
• Phép cộng 2 số nhị phân không dấu
34
Phép Nhân
• Nhân 2 số nhị phân 1-bit
A B A * B
0
0
1
1
0
1
0
1
0
0
0
1
35
Phép Nhân
• Phép nhân 2 số nhị phân không dấu
36
• Quy tắc thực hiện phép trừ như sau:
0 - 0 = 0 
1 - 1 = 0 
1 - 0 = 1 
[1]0 - 1 = 1 Mượn1
• VD: Thực hiện phép trừ 2 số nhị phân 5 bits: 00111
từ 10101
00111 7
10101 21
01110 14=
Phép Trừ
Biểu diễn số có dấu
• Phương pháp biểu diễn số có dấu
• Dạng số bù 1
• Dạng số bù 2
• Chuyển dạng số bù 2 sang số nhị phân
• Các phép tính trong hệ thống số bù 2
• Hiện tượng TRÀN (Overflow)
38
Biểu diễn số có dấu
• Số dương (+) và Số âm (-)
• Sử dụng thêm 1 bit (sign bit) để thể hiện dấu của số:
– 0: dương
– 1: âm
• Bit thể hiện dấu nằm ở ngoài cùng bên trái của số
39
Biểu diễn số có dấu
Có rất nhiều phương pháp để biểu diễn số có dấu:
• Dấu và độ lớn
• Dạng số bù 1
• Dạng số bù 2
• Số quá-K
• Cơ số nền -2
• Bảng so sánh
• 
40
Phương pháp “dấu và độ lớn”
• Ví dụ: biểu diễn 1 số 6 bits có dấu
+52
-52
41
Phương pháp dạng số bù 1 và bù 2
• Dạng số bù 2 là một trong những cách phổ biến nhất
được sử dụng để biểu diễn số có dấu.
Binary
1’s 
complement
2’s 
complement
Ex:
0 1_ 0 0 1 0 _0 1 0 0 (29210)
Negate each bit
1 0_ 1 1 0 1_ 1 0 1 1 (-29210)
Add 1
1 0 1 1 0 1 1 1 0 0 (-29210) 
+1
42
Biểu diễn số có dấu dưới dạng bù 2
+45
-45
43
Ví Dụ
• Biển diễn số có dấu áp dụng phương pháp dạng số bù 2
(a) +13
(b) -9
(c) -2
(d) -8
44
Chuyển đổi số bù 2 sang số nhị phân
Binary
2’s 
complement
Binary
Ví dụ:
1 0 1 1 0
0 1 0 1 0
Negate each bit
Add 1
1 0 1 1 0 
Negate each bit
Add 1
45
Phép cộng trong hệ thống số bù 2
• Thực hiện như phép cộng số nhị phân
– Bit dấu được xử lý dựa theo cách tương tự như các
bit độ lớn
– Bit nhớ ở vị trí cuối cùng sẽ được loại bỏ
– Nếu kết quả phép tính là số âm, thì đó chính là số
dạng bù 2
46
Ví Dụ
47
Ví Dụ
• Thực hiện phép cộng 2 số thập phân: +9 và -9?
48
Phép trừ trong hệ thống số bù 2
• Trong ví dụ 4 + (–9), phép cộng trong hệ thống số
bù 2 thực chất là phép trừ
• Quy tắc thực hiện phép trừ trong hệ thống số bù 2:
- B = bù 2 của B
A – B = A + (-B) = A + (bù 2 của B)
49
Ví Dụ
• 9 – 4 = ?
50
Hiện tượng tràn số học
Tràn
• Khi số bit của kết quả vượt quá số bit cho phép 
 Carry (thường dùng với số không dấu (unsigned number))
• Khi bit dấu của kết quả không đúng với bit dấu được dự đoán 
 Overflow (thường dùng với số có dấu (signed number))
1 số có dấu n-bit biểu diễn trong tầm: -2n-1 đến +2n-1-1 
– Hiện tượng Overflow luôn cho 1 kết quả sai hoàn toàn
=>Một mạch điện riêng biệt được thiết kế ra để phát hiện hiện tượng tràn
51
Ví dụ hiện tượng Tràn (overflow)
• Số có 4 bit, gồm 3 bit độ lớn và 1 bit dấu
• Hiện tượng Tràn không xảy ra đối với những phép tính
giữa 2 số khác dấu nhau
O
O
Các hệ thống số khác
• BCD
• Số dấu chấm động
• ASCII
53
BCD (Binary coded decimal)
• Mỗi chữ số của số thập phân được biểu diễn
bằng số nhị phân 4 bits tương ứng
• Ex: 84710 => BCD1010 => BCD
54
BCD và Số Nhị Phân
• BCD sử dụng nhiều bits hơn nhưng việc chuyển đổi
đơn giản hơn
13710 = 100010012 (Số Nhị Phân)
 Decimal: 1 * 27 + 1 * 23 + 1 * 20
13710 = 0001_0011_0111 (BCD)
 Decimal: 1 3 7
55
BCD
• Mạch thí nghiệm chuyển đổi
từ số thập phân sang số BCD
56
• Ký hiệu dấu chấm động có thể biểu diễn cho một số
có giá trị rất lớn hay rất nhỏ bằng cách sử dụng một
hình thức ký hiệu khoa học
• Ví dụ minh họa 1 số dấu chấm động 32-bit có độ
chính xác đơn.
S E (8 bits) F (23 bits)
Sign bit Magnitude with MSB dropped Biased exponent (+127)
(IEEE 754 Standard) 
Số dấu chấm động
57
Số dấu chấm động
Biểu diễn giá trị của tốc độ ánh sáng, c, bằng ký hiệu của số
dấu chấm động có độ chính xác đơn (c = 0.2998 x 109) 
Ký hiệu khoa học, 
c = 1._0001_1101_1110_1001_0101_1100_0000 x 228. 
C = 0 10011011 0001_1101_1110_1001_0101 _110 
Số Nhị Phân , c = 0001_0001_1101_1110_1001_0101_1100_00002. 
S = 0 // số dương
E = 28 + 127 = 15510 = 1001 10112. (IEEE 754, bias = 127)
F là 23 bits tiếp theo sau khi bit có giá trị 1 đầu tiên xuất hiện.
32-bit độ chính xác đơn (phần cứng)
58
ASCII
59
Byte
Floating-point 
number
Hexadecimal
Octal
BCD
1 byte gồm có 8 bits
Một số được đại diện dựa trên ký hiệu khoa học, trong đó bao
gồm phần số mũ và phần định trị
Hệ thống số có cơ số là 16
Hệ số có cơ số nền là 8
Binary Coded Decimal: là các mã số, trong đó mỗi chữ số
thập phân, từ 0 đến 9, được đại diện bởi một nhóm bốn bit
Alphanumeric
(chữ-số)
ASCII
Bao gồm các chữ số, chữ cái, và các ký hiệu khác
Mã tiêu chuẩn của Mỹ dùng trong việc trao đổi thông tin,
mã chữ và số được sử dụng rộng rãi nhất.
Thuật ngữ kỹ thuật số