Bài giảng Nhập môn An toàn thông tin - Chương III: Các hệ mật khóa công khai - Nguyễn Linh Giang
Đặc điểm
– Mật mã công khai dựa trên cơ sở của các hàm
toán học.
– Không dựa trên phép thay thế và đổi chỗ như
trong phương pháp mã hoá đối xứng.
– Mã mật công khai là bất đối xứng.
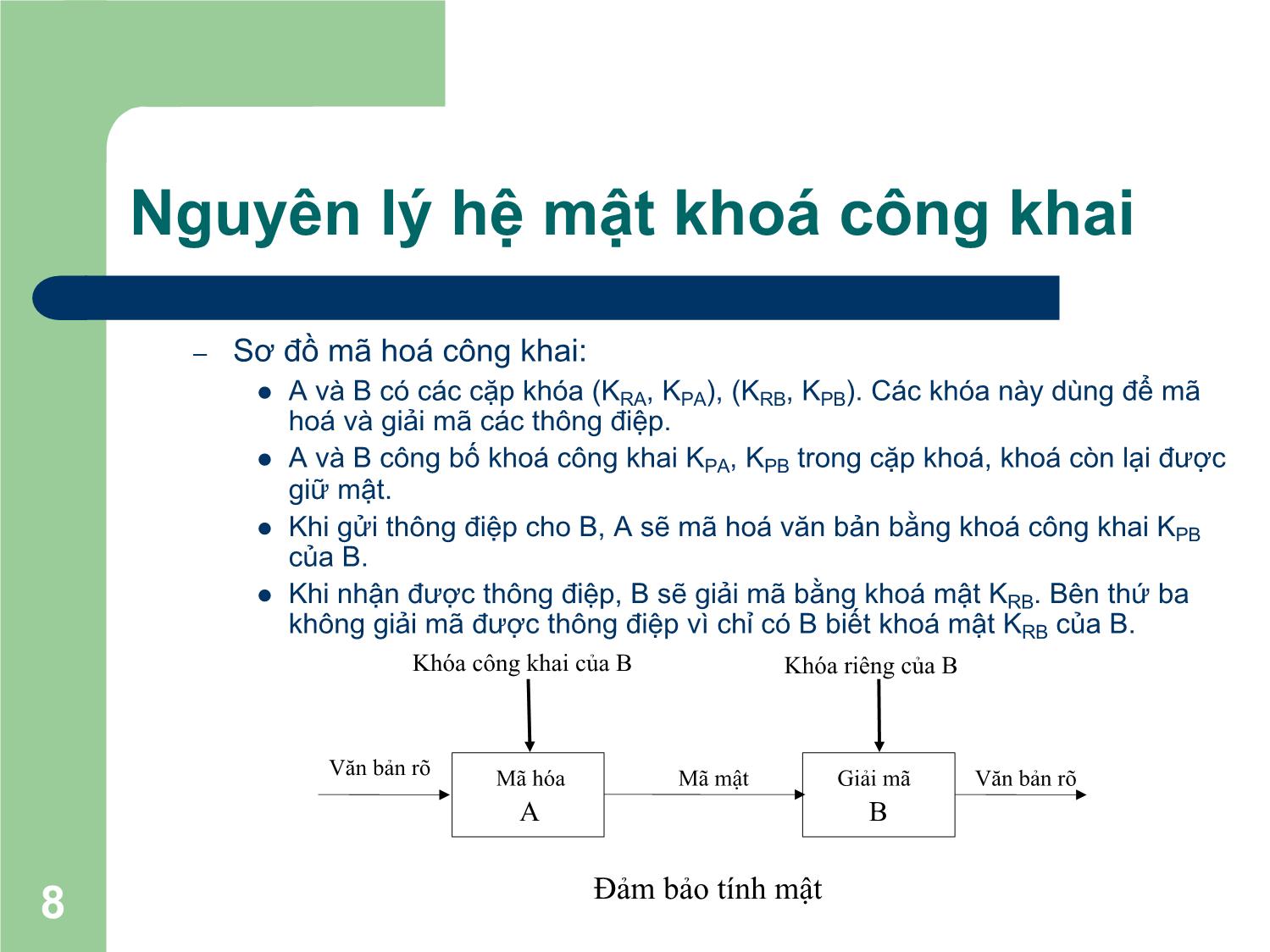
l Trong cơ chế mã mật khoá công khai sử dụng hai khoá:
khoá mật và khoá công khai.
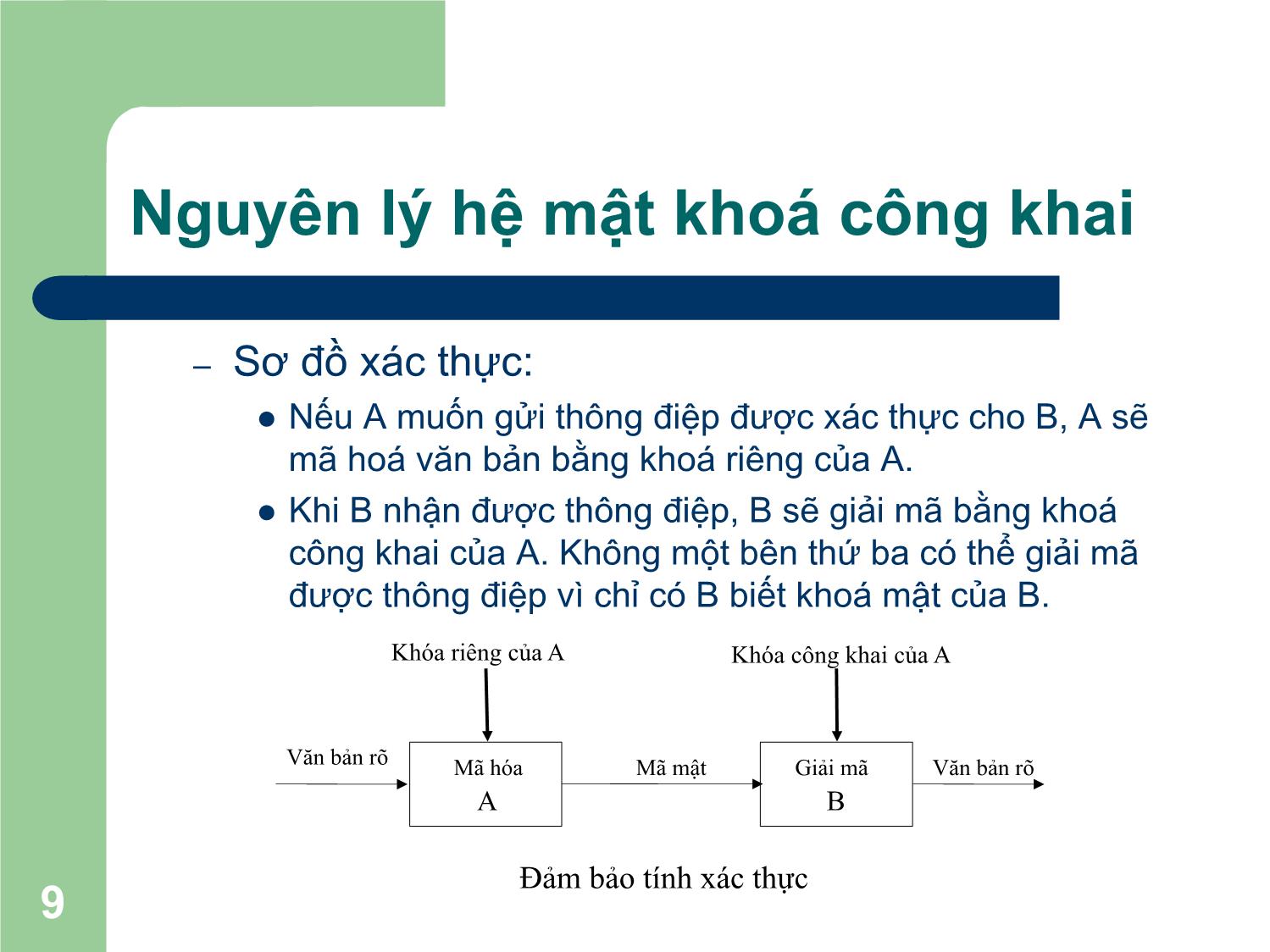
l Các hệ quả của việc sử dụng hai khoá bất đối xứng:
tính toàn vẹn, tính xác thực, phân phối khoá.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Nhập môn An toàn thông tin - Chương III: Các hệ mật khóa công khai - Nguyễn Linh Giang", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Nhập môn An toàn thông tin - Chương III: Các hệ mật khóa công khai - Nguyễn Linh Giang

Nhập môn An toàn thông tin PGS. Nguyễn Linh Giang Bộ môn Truyền thông và Mạng máy tính Nội dung I. Nhập môn An toàn thông tin II. Đảm bảo tính mật I. Các hệ mật khóa đối xứng (mã hóa đối xứng) II. Các hệ mật khóa công khai ( mã hóa bất đối xứng ) III. Bài toán xác thực I. Cơ sở bài toán xác thực II. Xác thực thông điệp III. Chữ ký số và các giao thức xác thực IV. Các cơ chế xác thực trong các hệ phân tán IV. An toàn an ninh hệ thống I. Phát hiện và ngăn chặn xâm nhập ( IDS, IPS ) II. Lỗ hổng hệ thống 2 Nội dung l Tài liệu môn học: – W. Stallings “Networks and Internetwork security” – W. Stallings “Cryptography and network security” – Introduction to Cryptography – PGP – D. Stinson – Cryptography: Theory and Practice 3 Chương III. Các hệ mật khóa công khai l Nguyên lý hệ mật khoá công khai l Thuật toán RSA l Sơ đồ trao đổi khoá Diffie-Hellman l Một số hệ mật khóa công khai khác 4 Nguyên lý hệ mật khoá công khai l Đặc điểm – Mật mã công khai dựa trên cơ sở của các hàm toán học. – Không dựa trên phép thay thế và đổi chỗ như trong phương pháp mã hoá đối xứng. – Mã mật công khai là bất đối xứng. l Trong cơ chế mã mật khoá công khai sử dụng hai khoá: khoá mật và khoá công khai. l Các hệ quả của việc sử dụng hai khoá bất đối xứng: tính toàn vẹn, tính xác thực, phân phối khoá. 5 Nguyên lý hệ mật khoá công khai l Xuất xứ: – Hệ mã mật khoá công khai được phát triển nhằm giải quyết hai vấn đề phức tạp nảy sinh từ phương pháp mã hoá đối xứng: l Vấn đề thứ nhất: bài toán phân phối khoá; l Vấn đề thứ hai: chữ ký số. 6 Nguyên lý hệ mật khoá công khai l Hệ mật khoá công khai. – Sơ đồ mã mật khoá công khai sử dụng một khoá để mã hoá và một khoá khác có liên quan để giải mã. Các thuật toán mã hoá và giải mã có một số đặc điểm quan trọng sau: l Không thể xác định được khoá giải mã nếu chỉ biết thuật toán mã hoá và khoá mã hoá. l Một số hệ mã mật khoá công khai ( như RSA ) còn cung cấp khả năng sử dụng bất kỳ một khoá trong cặp khoá làm khoá mã hoá thì khoá còn lại sẽ được dùng làm khoá giải mã. 7 Nguyên lý hệ mật khoá công khai – Sơ đồ mã hoá công khai: l A và B có các cặp khóa (KRA, KPA), (KRB, KPB). Các khóa này dùng để mã hoá và giải mã các thông điệp. l A và B công bố khoá công khai KPA, KPB trong cặp khoá, khoá còn lại được giữ mật. l Khi gửi thông điệp cho B, A sẽ mã hoá văn bản bằng khoá công khai KPB của B. l Khi nhận được thông điệp, B sẽ giải mã bằng khoá mật KRB. Bên thứ ba không giải mã được thông điệp vì chỉ có B biết khoá mật KRB của B. Khóa công khai của B Khóa riêng của B Văn bản rõ Mã hóa Mã mật Giải mã Văn bản rõ A B 8 Đảm bảo tính mật Nguyên lý hệ mật khoá công khai – Sơ đồ xác thực: l Nếu A muốn gửi thông điệp được xác thực cho B, A sẽ mã hoá văn bản bằng khoá riêng của A. l Khi B nhận được thông điệp, B sẽ giải mã bằng khoá công khai của A. Không một bên thứ ba có thể giải mã được thông điệp vì chỉ có B biết khoá mật của B. Khóa riêng của A Khóa công khai của A Văn bản rõ Mã hóa Mã mật Giải mã Văn bản rõ A B Đảm bảo tính xác thực 9 Nguyên lý hệ mật khoá công khai l Các yêu cầu đối với hệ mật khóa công khai – Quá trình sinh cặp khóa KP, KR là dễ trên phương diện tính toán; – Quá trình mã hóa bản tin bằng khóa công khai KP ở bên gửi là dễ: Y = EKP(M); – Quá trình giải mã ra văn bản rõ khi biết khóa riêng KR và bản tin mật Y là dễ: M = DKR(Y); – Đối với thám mã, nếu chỉ biết KP sẽ rất khó trên phương diện tính toán để tính ra KR; – Đối với thám mã, nếu chỉ biết KP và bản tin mật Y sẽ rất khó trên phương diện tính toán để tính ra bản tin rõ M; – Nguyên lý đối xứng: quá trình mã hóa – giải mã có thể áp dụng theo hai chiều: M = DKP[EKR(M)] 10 Nguyên lý hệ mật khoá công khai l Các ứng dụng của hệ mật khóa công khai – Ứng dụng trong mật mã – mã hóa, giải mã (RSA): l Bên gửi mã hóa bằng khóa công khai của bên nhận; l Bên nhận giải mã bằng khóa riêng. – Ứng dụng trong phân phối khóa(RSA, Diffie-Helman): duy trì kênh mật phân phối khóa đối xứng bằng cơ sở mã mật công khai; – Ứng dụng trong chữ ký số (RSA, DSS): l Bên gửi ký bằng khóa riêng. l Bên nhận xác thực chữ ký bằng khóa công khai của bên gửi. 11 Thuật toán mã hoá công khai RSA l Cơ sở lý thuyết số l Sơ đồ thuật toán l Thám mã RSA 12 Sơ đồ thuật toán RSA l Xuất xứ – RSA do Ron Rivest, Adi Shamir và Len Adlenman phát minh năm 1977; – Hệ thống mã khoá công khai phổ biến và đa năng: l Được sử dụng trong các ứng dụng mã hóa/giải mã; l Chứng thực; l Phân phối và trao đổi khoá. 13 Sơ đồ thuật toán RSA l Thuật toán RSA: – Phương pháp mã hóa khối; – Văn bản rõ và văn bản mật là các số nguyên có giá trị từ 0 đến n-1, n – số nguyên lớn; – Mỗi khối có giá trị nhỏ hơn n. – Kích thước của khối (số bít) nhỏ hơn hoặc bằng log2(n). – Thực tế, kích thước của khối là k bit với 2k < n ≤ 2k+1. 14 Sơ đồ thuật toán RSA – Cặp khóa: (e, d) – Mã hoá Bản rõ M < n Mã mật C = Me mod n – Giải mã Mã mật C Bản rõ M = Cd mod n = (Me)d mod n 15 Sơ đồ thuật toán RSA – Bên gửi và bên nhận phải biết số n. – Bên gửi biết khóa công khai là cặp (e, n). – Bên nhận có khóa riêng là cặp (d, n). – Các yêu cầu: l Có thể tìm được các số e, d, n sao cho: Med = M mod n " M < n. l Thực hiện tính Me và Cd một cách đơn giản " M < n. l Không thể xác định được d nếu biết e và n 16 Sơ đồ thuật toán RSA l Tạo khoá – Tìm các số e, d sao cho: Med=M mod n – Hệ quả của định lý Euler: cho p và q là số nguyên tố, n và m là hai số nguyên sao cho: n=pq và 0 < m < n, k là số nguyên bất kỳ. Đẳng thức sau nghiệm đúng: mkf(n)+1=mk(p-1)(q-1)+1ºm mod n – Như vậy: ed = kf(n)+1, tức là: – ed º1 mod f(n) hay d ºe-1 mod f(n) có nghĩa là gcd(f(n), d) = 1 và gcd(f(n), e) = 1 17 Sơ đồ thuật toán RSA – Sơ đồ tạo khóa RSA 18 Sơ đồ thuật toán RSA – Ví dụ l p = 7, q = 17 l n = pq = 119; f(n)=(p-1)(q-1)=96 l Chọn e nguyên tố cùng nhau với f(n), nhỏ hơn f(n), – Chọn e = 5; l Tìm d: dºe-1 mod f(n) – d=77 => cặp khóa: e=(5, 119); d=(77, 119) 19 Sơ đồ thuật toán RSA l Mã hoá và giải mã – Vấn đề trong thuật toán mã hoá và giải mã RSA là việc thực hiện phép toán luỹ thừa và phép toán đồng dư với số nguyên lớn. – Giải quyết dựa trên tính chất của phép toán mođun: [(a mod n) x (b mod n)] mod n = (a x b) mod n – Tính am với m lớn. i l Biểu diễn nhị phân của m =bkbk-1b0=åbi≠02 l Do đó: æ ö ç 2i ÷ ç å ÷ i am = aè bi¹0 ø = Õa2 bi ¹0 i i am mod n = Õa2 mod n = Õ(a2 mod n) 20 bi ¹0 bi ¹0 Sơ đồ thuật toán RSA l Sinh khoá – Các bước quan trọng trong tạo khóa: l Xác định 2 số nguyên tố p và q. Để tránh tấn công vét cạn, p và q phải lớn. l Xác định e và d - Xác định số nguyên tố p, q (sử dụng thuật toán Miller – Rabin) 1. Chọn một số nguyên lẻ n ngẫu nhiên (sử dụng bộ sinh số giả ngẫu nhiên). 2. Chọn một số nguyên a < n ngẫu nhiên. 3. Thực hiện thuật toán xác suất để kiểm tra số nguyên tố. Nếu n test thành công thì loại bỏ giá trị n và quay lại bước 1. 4. Nếu n test thành công với số lượng test đủ, chấp nhận n; mặt khác, quay lại bước 2. - Chọn e và tính d từ e và f(n) (sử dụng thuật toán Euclid) 21 Thám mã RSA l Tấn công vét cạn: thử vét cạn toàn bộ không gian khóa riêng. l Tấn công toán học: thực hiện bài toán phân tích số nguyên thành tích hai số nguyên tố. l Tấn công dựa vào thời gian: dựa vào thời gian để thực hiện thuật toán giải mã. 22 Thám mã RSA - tấn công vét cạn l Phương pháp: thực hiện vét cạn toàn bộ không gian khoá. l Biện pháp đối phó: – Sử dụng không gian có khoá kích thước lớn, tức là tăng số bít của d và e. – Không gian khóa có kích thước lớn sẽ làm quá trình sinh khoá, mã hoá, giải mã thực hiện chậm đi. 23 Thám mã RSA - Tấn công toán học l Các phương pháp tấn công toán học vào RSA: – Phân tích n thành tích hai số nguyên tố p và q; l Sau đó cho phép tính f(n)=(p-1)(q-1); l Từ f(n) có thể tính d=e-1 mod f(n). – Xác định f(n) trực tiếp không qua p và q; -1 l Cho phép từ f(n) có thể tính d=e mod f(n). – Xác định trực tiếp d không qua tính f(n). 24 Thám mã RSA - Tấn công toán học l Trường hợp đơn giản nhất là người thám mã biết được f(n) l Phân tích n thành tích của 2 thừa số nguyên tố: Có nhiều thuật toán phân tích n thành hai thừa số nguyên tố. – Có ba thuật toán hiệu quả trên các số rất lớn: l Thuật toán sàng bình phương (quadratic sieve), l Đường cong elip (elliptic curve) và l Sàng trường số. – Các thuật toán được biết đến nhiều trước đây: l Thuật toán p – 1 của Pollard, l Thuật toán p + 1 của William, l Thuật toán chia nhỏ liên tiếp 25 l Thuật toán chia thử. Thám mã RSA - Tấn công toán học l Những yêu cầu đối với p và q: – p và q chỉ nên khác nhau về độ dài khoảng vài hàng số nhị phân và trong khoảng từ 1075 đến 10100; – (p-1) và (q-1) phải có những thừa số nguyên tố lớn; – Gcd(p-1, q-1) phải nhỏ. – Thực tế cho thấy, nếu e < n và d < n1/4 thì d có thể dễ dàng tính được! 26 Thám mã RSA - Tấn công dựa thời gian l Nội dung của phương pháp này dựa vào việc theo dõi thời gian thực hiện thuật toán giải mã; – Có thể áp dụng đối với những hệ mật khóa công khai khác! – Là dạng tấn công chỉ sử dụng mã mật (ciphertext only attack) l Biện pháp đối phó: – Thời gian tính mũ là hằng: Làm cho thời gian tính mũ là như nhau trước khi trả về kết quả. Biện pháp này đơn giản nhưng làm giảm hiệu năng. – Thực hiện trễ ngẫu nhiên: Thêm các trễ thời gian ngẫu nhiên vào thuật toán mũ hoá. – Làm mù: Nhân văn bản mật với một số ngẫu nhiên trước khi thực hiện mũ hoá. Khi đó thám mã sẽ không biết bit nào của mã mật được xử lý và do đó ngăn chặn được quá trình phân tích mã mật. 27 Lý thuyết số l Số học modun l Định lý Euler và định lý Fermat l Kiểm tra số nguyên tố l Thuật toán Euclid l Định lý số dư Trung Hoa l Sinh giả ngẫu nhiên các số nguyên lớn 28 Số học modun l Định lý về số dư. Cho một số nguyên dương n và một số nguyên a. Khi đó tồn tại duy nhất các số q và r với , sao cho a = qn + r. r gọi là số dư của phép chia a cho n. l Định nghĩa số dư. Cho một số nguyên dương n và số nguyên a. Ký hiệu a mod n là số dư khi chia a cho n. a = x n + (a mod n) l Định nghĩa 2. Hai số a và b được gọi là đồng dư theo mođun n nếu a mod n = b mod n, a º b (mod n) l Ví dụ: 11 = 1 x 7 + 4 => 11 mod 7 = 4 -11 = (-2) x 7 + 3 => -11 mod 7 = 3 73 º 4 (mod 23) 29 Định lý Euler và định lý Fermat l Định lý nhỏ Fermat: Nếu p là số nguyên tố và a là số nguyên dương không chia hết cho p thì ap1- º 1(mod p) l Hàm Euler – Hàm Euler được ký hiệu là f(n) là số các số nguyên dương nhỏ hơn n và nguyên tố cùng nhau với n – Nếu p là số nguyên tố, f(p) = p – 1 – Nếu p,q ÎP, n = pXq, thì f(n) = (p – 1)X(q – 1) l Định lý Euler: Nếu hai số nguyên a và n nguyên tố cùng nhau, ta có af(n)º 1 (mod n) 30 Kiểm tra số nguyên tố nĐịnh lý l Chứng minh - Xét trường hợp (x + 1), (x – 1) đồng thời chia hết cho p. - Xét trường hợp (x - 1) chia hết cho p. - Tương tự xét trường hợp (x + 1) chia hết cho p ta suy ra x -1 (mod p) l Kết quả suy ra 31 1.3 Kiểm tra số nguyên tố (tiếp) l Thuật toán Miller, Rabin: kiểm tra một số có phải là một số nguyên tố không dựa vào kết quả của định lý trên. Input của thuật toán là số nguyên n và một số nguyên a nào đó nhỏ hơn n. Nếu WITNESS có giá trị trả về là TRUE thì n không phải là số nguyên tố, nếu WITNESS có giá trị trả về là FALSE thì n có thể là số nguyên tố l Ví dụ l Đánh giá độ phức tạp 32 Thuật toán Euclid l Tìm ước số chung lớn nhất - Định lý - Chứng minh - Ví dụ - Đánh giá độ phức tạp 33 Thuật toán Euclid (tiếp) l Tìm phần tử đối xứng Thuật toán Euclid mở rộng sẽ trả về phần tử đối xứng của d nếu gcd(d, f) = 1. 34 Định lý số dư Trung Hoa l Định lý § Hai kết quả của định lý số dư Trung Hoa § Ứng dụng của định lý số dư Trung Hoa § Ví dụ 35 Sinh giả ngẫu nhiên các số nguyên lớn l Bộ sinh số giả ngẫu nhiên Kỹ thuật được sử dụng rộng rãi trong việc sinh giả ngẫu nhiên là phương pháp đồng dư tuyến tính lần đầu tiên được đề xuất bởi Lehmer. l Sinh số giả ngẫu nhiên dựa trên kỹ thuật mật mã l Bộ sinh số giả ngẫu nhiên Blum Blum Shub 36 Hệ mật Diffie-Hellman l Các sơ đồ quản lý khoá của hệ mật khoá công khai – Quản lý và chứng thực khoá công khai; – Cấp phát chứng thư số; – Trao đổi khoá mã hoá-giải mã của hệ mật khoá đối xứng: l Xây dựng kênh truyền bí mật để trao đổi phiên. – Dùng cơ chế bảo mật của hệ mật khoá công khai; 37 Nguyên lý trao đổi khóa Diffie-Hellman l Được Diffie-Hellman đưa ra vào 1976 l Là sự kết hợp của hai mô hình xác thực và mật của hệ KCK l Việc sinh ra các cặp khoá là hoàn toàn khác nhau đối với người sử dụng l Sử dụng cơ chế trao đổi khoá trực tiếp không qua trung gian xác thực 38 Nguyên lý trao đổi khóa Diffie-Helman l Sử dụng trong các ứng dụng trao đổi khoá khi sử dụng hệ mật khoá đối xứng. l Nguyên tắc: hai người sử dụng có thể trao đổi khoá phiên an toàn - được dùng để mã hoá và giải mã các thông điệp; l Thuật toán tự giới hạn chỉ dùng cho các ứng dụng sử dụng kĩ thuật trao đổi khoá; 39 Cơ sở hình thành thuật toán l Nguyên tắc toán học : – m là một số nguyên tố: – y=ai mod m là bài toán dễ; – Bài toán ngược là bài toán khó. Đặc biệt với m lớn. l Dựa trên phép tính logarit rời rạc 40 Thuật toán logarit rời rạc l Thuật toán logarit rời rạc: – Một số nguyên tố p; – Một gốc nguyên thuỷ a của p : là các số mà luỹ thừa của a theo modul p thuộc (1,p-1) – Với b bất kì nguyên sẽ luôn $i sao cho b= ai mod p. 41 Thuật toán Diffie-Hellman 42 Thuật toán trao đổi khoá 43 Tính bảo mật của hệ mật l Thám mã có sẵn các thông tin :p,a,Yi,Yj l Để có thể giải được K ,X bắt buộc thám mã phải sử dụng thuật toán logarit rời rạc : rất khó nếu p lớn l Vì thế nên chọn p càng lớn càng tốt : như thế thì việc tính toán ra X coi như không thể 44 Hệ mật và thám mã l Thám mã có thể tấn công vào các thông tin : p ,a,Yj,Yj l Và sử dụng thuật toán rời rạc để tính ra X, sau đó tính ra K l Quan trọng nhất là độ phức tạp của thuật toán logarit phụ thuộc vào chọn số nguyên tố p l Tấn công man in the middle 45 Lĩnh vực ứng dụng l Tự quá trình thuật toán đã hạn chế ứng dụng chỉ sử dụng cho quá trình trao đổi khoá mật là chủ yếu l Sử dụng trong chữ kí điện tử. l Các ứng dụng đòi hỏi xác thực người sử dụng. 46
File đính kèm:
 bai_giang_nhap_mon_an_toan_thong_tin_chuong_iii_cac_he_mat_k.pdf
bai_giang_nhap_mon_an_toan_thong_tin_chuong_iii_cac_he_mat_k.pdf

