Bài giảng Nhập môn An toàn thông tin - Chương II: Các phương pháp mật mã khóa đối xứng - Nguyễn Linh Giang
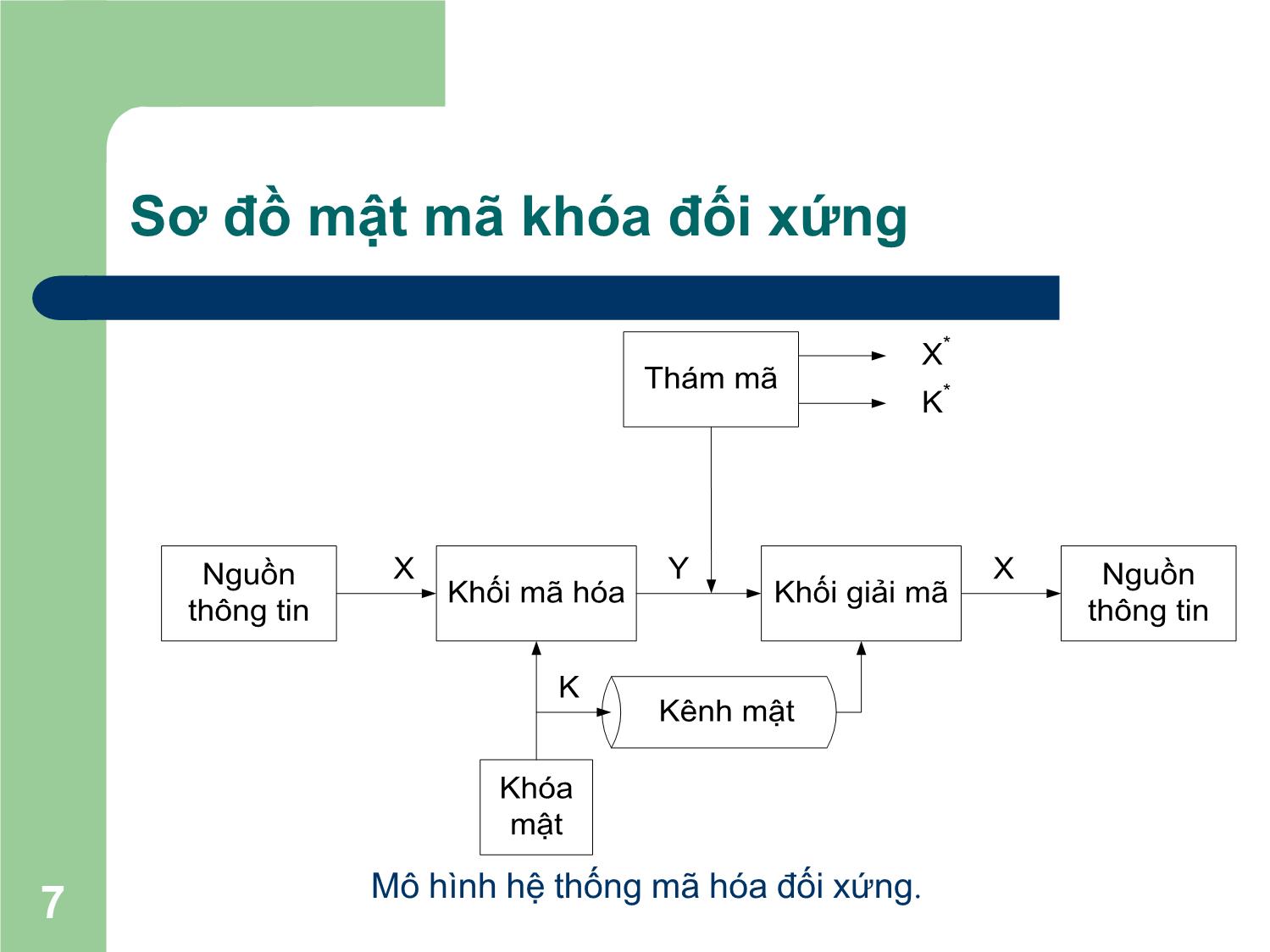
1. Sơ đồ chung của phương pháp mật mã khóa đối xứng
2. Một số phương pháp mật mã khóa đối xứng kinh điển
3. Hệ mật hoàn hảo và không hoàn hảo
4. Phương pháp DES
5. Quản trị và phân phối khóa
6. Đảm bảo tính riêng tư sử dụng phương pháp mật mã
khoá đối xứng

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Nhập môn An toàn thông tin - Chương II: Các phương pháp mật mã khóa đối xứng - Nguyễn Linh Giang", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Nhập môn An toàn thông tin - Chương II: Các phương pháp mật mã khóa đối xứng - Nguyễn Linh Giang

sơ đồ mã sử dụng một lần ( one-
time pad ): không thể phá khoá. Đầu ra độc lập thống
kê với bản rõ.
– Vấn đề nảy sinh: tính mật cho quá trình trao đổi khoá
37
Một số phương pháp mã hóa đối
xứng kinh điển
l Đảm bảo an toàn dữ liệu: nhiều thuật toán mật mã.
l Ðánh giá một thuật toán mật mã theo:
– Tính mật, độ phức tạp, tốc độ thực hiện thuật toán, sơ đồ
phân phối khoá.
l Các phương pháp mật mã kinh điển như phương pháp
mã hoá thay thế, hoán vị còn đơn giản.
– Nhược điểm:
l Độ an toàn thấp vì không đạt độ phức tạp cần thiết;
l Dễ bị lộ khoá do cả người gửi và người nhận đều sử dụng cùng một
khoá => cần pha phân phối khoá dễ bị tấn công
38
Phương pháp mật mã DES
l Bản rõ X, bản mã mật Y là các chuỗi nhị phân độ dài
64 bit.
l Khóa K có độ dài 56 bit.
l Từng khối 64 bit được mã hóa độc lập sử dụng
chung một khóa.
39
Phương pháp mật mã DES
l Phương pháp S-DES( DES giản lược )
l Phương pháp mật mã DES
40
S- DES
(Simplified data encryption standard)
l Cấu trúc của DES là rất phức tạp
– S-DES - phiên bản đơn giản của DES;
– Cho phép:
l Mã hoá và giải mã bằng tay;
l Hiểu biết sâu về hoạt động chi tiết của giải thuật DES.
l S-DES đơn giản hơn nhiều so với DES
– Các tham số của S-DES nhỏ hơn trong DES;
l Do giáo sư Edward Schaefer thuộc trường đại học Santa
Clara phát triển
41
Thuật toán S-DES (Simplified DES)
ENCR YPTION DECRYPTION
10-bit key
8-bit plaintext
8-bit plaintext
P10
Shift
IP IP
P8
K1 K1
fk fk
Shift
SW SW
P8
K2 K2
fk fk
IP-1 IP-1
42
bit ciphertext 8-
8-bit ciphertext
Thuật toán S-DES (Simplified DES)
l Giải thuật mã hoá S-DES sử dụng phương
pháp mã hoá theo khối
l Đầu vào:
- 8-bit block của bản rõ
- 10-bit khoá
l Đầu ra:
- 8-bit của bản mã
43
Thuật toán S-DES
l Thuật toán mã hoá bao gồm 4 hàm:
- Hàm IP(Initial Permutation)
- Hàm fk
- Hàm SW (Switch)
- Hàm IP-1
l Thuật toán mã hoá::
ciphertext=IP-1(f(SW(f(IP(plaintext)))))
l Thuật toán giải mã :
plaintext =IP (f(SW(f(IP-1 (ciphertext)))))
44
Thuật toán S-DES (Simplified DES)
Sinh khoá trong S-DES
10-bit key
P10
5 5
LS-1 LS-1
5 5
P8
8
LS-2 LS-2
5 5
P8
8
45
Thuật toán S-DES (Simplified DES)
Các hàm sinh khoá:
l P10:Đây là hàm hoán vị tuân theo luật như trong bảng
l LS-1: Là hàm dịch vòng 1 bit
l LS-2: Là hàm dịch vòng 2 bit
l P8:Là hàm hoán vị tuân theo luật như trong bảng
46
Thuật toán S-DES Mã hoá S-DES:
Hàm IP và hàm IP-1:
+ Hàm IP tuân theo luật sau:
+ Hàm IP-1 tuân heo luật sau:
47
Thuật toán S-DES Hàm fk:
8-bit plaintext
IP
4
4
E/P
fk
F
8 8
+ K1
4
4
S0 S0
2
2
P4
4
+
48 4
Thuật toán S-DES
E/P(expension/permutation):
l Hàm E/P tuân theo luật sau:
l Nếu gọi 4 bit đầu vào là (n1,n2,n3,n4) thì E/P được
biểu diễn chi tiết như sau:
49
Thuật toán S-DES
Khối thay thế S-box
l Đầu vào S-box: khối 8 bit được chia thành hai khối 4 bit;
l Mỗi khối 4 bit được đưa vào S0 và S1
l Thay thế mỗi khối 4 bit bằng khối 2 bit;
l Các khối S0 và S1 được định nghĩa như sau:
S0: S1:
50
Thuật toán S-DES
Khối thay thế S-box
l Phần tử trong khối S-box có độ dài 2 bit;
l Quá trình thay thế trong S-box:
– Với 4 bit đầu vào là (b1,b2,b3,b4);
l b1 và b4 kết hợp thành một số chỉ hàng của S
box,
l b2 và b3 tạo thành số chỉ cột trong S box;
l Phần tử nằm trên hàng và cột đã xác định thay
thế cho 4 bit đầu vào của S-box đó.
51
Thuật toán S-DES
Hoán vị P4
l Hoán vị P4 tuân theo luật sau:
52
Thuật toán S-DES
Hàm SW
l Hàm fk chỉ thực hiện trên 4 bit trái của đầu
vào;
l Hàm SW hoán đổi 4 bit phải và 4 bit trái để
lần áp dụng hàm fk thứ 2 sẽ thực hiện trên 4
bit phải.
l Áp dụng hàm fk lần 2 thực hiện các hàm E/P
,S0,S1,P4 như trên.
53
Mật mã DES
(Data Encryption Standard)
l Phương pháp mật mã DES được Ủy ban tiêu chuẩn Mỹ
(U.S National Bureau for Standards) công bố năm 1971
để sử dụng trong các cơ quan chính phủ liên bang.
l Thuật tóan được IBM phát triển.
l DES có một số đặc điểm sau:
– Sử dụng khoá 56 bít.
– Xử lý khối vào 64 bít, biến đổi khối vào thành khối ra 64 bít.
– Mã hoá và giải mã được sử dụng cùng một khoá.
– DES được thiết kế để thực hiện hiệu quả bằng phần cứng.
– DES thường được sử dụng để mã hoá các dòng dữ liệu mạng
và mã hoá dữ liệu được lưu trữ trên đĩa.
54
Giải mã DES
l Với DES, có thể sử dụng cùng chức
năng để giải mã hoặc mã hoá một khối.
l Điểm khác biệt: khi giải mã, các khoá
phải được sử dụng theo thứ tự ngược
lại.
55
Độ an toàn của DES
l Độ an tòan hệ mật khoá đối xứng phụ thuộc hai tham số: độ
phức tạp của thuật toán và độ dài của khoá.
l Khoá có độ dài 56 bít, không gian khóa sẽ có 256 khoá có
thể sử dụng.
l Nếu tính mật của phương pháp chỉ phụ thuộc vào độ phức
tạp của thuật toán.
– Có nghĩa rằng sẽ không có phương pháp nào khác để phá hệ
thống mật mã ngoài cách thử mọi tổ hợp khoá có thể: phương
pháp tấn công vét cạn (brute-force attack).
– Nếu một siêu máy tính có thể thử một triệu khoá trong một
giây, thì thời gian tổng cộng để để tìm ra khoá đúng là khoảng
2000 năm.
56
Kết luận
l DES đã được phân tích kỹ lưỡng và công nhận là vững chắc. Các
hạn chế của nó đã được hiểu rõ và có thể xem xét trong quá trình
thiết kế.
– Để tăng độ an toàn của DES, sử dụng các hệ thống mật mã DES mở
rộng
– DES mở rộng khoá có thể là 128 bít, 192 bít,... độ lớn khối có thể là
128 bít. Do vậy, độ an toàn của DES mở rộng cao hơn rất nhiều.
57
Mật mã khối ( block cipher )
l Định nghĩa
– Mã khối là mật mã khóa đối xứng thực hiện trên
nhóm bit có độ dài cố định. Nhóm bit này được gọi
là một khối. Quá trình chuyển đổi không thay đổi.
– Khi mã hóa, mã khối có thể thực hiện trên từng khối
độ dài 128 bit của bản rõ tại đầu vào thứ nhất và cho
ra khối 128 bit của mã mật.
l Quá trình biến đổi được kiểm soát bằng đầu vào thứ hai:
khóa mật
– Quá trình giải mã thực hiện tương tự: nhận tại đầu
vào thứ nhất khối 128 bit của mật mã, khóa mật và
58 tại đầu ra ta nhận được khối 128 bit của bản rõ
Mật mã khối ( block cipher )
– Để mã hóa bản tin có độ dài lớnhơn kích thước khối,
( ví dụ 128 bit ), các chế độ xử lý ( mode of operation
) được sử dụng.
– Mã hóa khối tương phản với mã hóa dòng ( stream
cipher ), trong đó mỗi ký tự được thao tác một lần và
quá trình chuyển đổi thay đổi trong suốt quá trình mã
hóa.
– Ví dụ mã hóa khối:
l Thuật toán DES do công ty IBM xây dựng và công bố năm
1977.
l Hậu duệ của DES, Advanced Encryption Standard (AES), ra
đời năm 2001.
59
Mật mã khối
l Mã khối và mã dòng: mã theo từng khối bit và mã từng bit riêng rẽ
Plaintext= 010100110111= key 000 001 010 011 100 101 110 111
(010)(100)(110)(111) 0 001 111 110 000 100 010 101 011
Ciphertext = 111 011 000 101 1 001 110 111 100 011 010 000 101
theo key=1 2 001 000 100 101 110 111 010 011
Ciphertext = 100 011 011 111 3 100 101 110 111 000 001 010 011
4 101 110 100 010 011 001 011 111
theo key=4
l Số lượng key: 22 < 5 < 23 key cần có độ dài 3 bit để cho kích
thước khoá bang kích thước khối: key size= block size= 3.
l Kích thước khoá nhỏ: không an toàn.
l Nếu bên tấn công Eve bắt được thông điệp mật C=001, sẽ khó lựa
60 chọn P= 000 hay 101.
Mật mã khối ( block cipher )
l Mật mã khối gồm một cặp thuật toán:
– Thuật toán mã hóa, E, và
– Thuật toán giải mã, E-1.
– Cả hai thuật toán đều có hai đầu vào:
l Khối dữ liệu đầu vào kích thước n bit và
l Khóa độ dài k bit,
– Đầu ra là khối dữ liệu kích thước n-bit.
61
Mật mã khối ( block cipher )
l Sơ đồ mã hóa và giải mã khối
62
Mật mã khối ( block cipher )
l Đối với một khóa xác định, hàm giải mã là hàm
ngược của hàm mã hóa:
-1
EK ( EK ( M ) ) = M
Đối với mỗi khối M và khóa K.
l Với mỗi khóa K, EK là hoán vị ( song ánh ) trên
tập hợp các khối đầu vào. Mỗi khóa sẽ lựa
chọn một hoán vị từ tập hợp 2n! phần tử.
63
Mật mã khối
l Điều kiện để tạo mã khối an toàn:
– Kích thước khối phải đủ lớn để ngăn chặn tấn
công bang phân tích thống kê.
l Kích thước khối lớn sẽ làm chậm quá trình xử lý
– Không gian khoá (độ dài khoá) cần phải đủ lớn để
ngăn chặn tấn công vét cạn.
l Khoá không được có độ dài quá lớn – khó phân phối và
quản trị
64
Mật mã khối ( block cipher )
l Kích thước khối n, thông thường bằng 64 hoặc 128 bit,
– Một số mật mã khối có kích thước khối thay đổi.
l Kỹ thuật cho phép bản rõ với độ dài tùy ý được mã hóa: sơ đồ
padding.
l Mỗi chế độ làm việc có một đặc tính riêng biệt phụ thuộc vào sai
số truyền lan, tính dễ truy cập ngẫu nhiên và khả năng bị tổn
thương đối với từng loại tấn công cụ thể.
l Kích thước khóa k thường bằng 40, 56, 64, 80, 128, 192 và 256
bits.
– Đến năm 2006, độ dài khóa 80 bits thường được chọn là kích thước khóa tối
thiểu để ngăn chặn tấn công vét cạn ( brute force attacks ).
65
Mật mã khối
l Điều kiện để thiết kế các mã khối an toàn
– Hàm nhập nhằng (Confusion):
l Là hàm làm cho mối quan hệ giữa bản mật vào bản rõ đủ
phức tạp để đối phương không phát hiện được quy luật;
l Hàm này là hàm phi tuyến
l Thường dùng phép thế
– Hàm khuếch tán (Diffusion):
l Làm phân tán thông tin từ bản rõ vào toàn bộ bản mật;
l Sự thay đổi trong bản rõ sẽ ảnh hưởng tới nhiều phần của
bản mật
66 l Ngăn chặn tấn công bằng phân tích thống kê
l Thườngdùng hoán vị, đổi chỗ
Mật mã khối ( block cipher )
l Mã khối lặp
– Phần lớn các mật mã khối được
xây dựng trên cơ sở áp dụng lặp đi
lặp lại một hàm f đơn giản gồm thay
thế và hoán vị.
l Mỗi vòng lặp được gọi là một chu
kỳ ( round ) và hàm lặp được gọi là
hàm quay vòng. Thông thường số
lần quay vòng từ 4 đến 32 lần.
l Nhiều mật mã khối có thể được
phân loại thành các cấu trúc Feistel
- các mạng thay thế-hoán vị.
l Các phép toán số học, lôgic ( đặc
biệt là XOR ), các S-box và các
67 phép hoán vị thường được sử dụng
Mật mã khối
l Các thuộc tính của mật mã khối:
– Kích thước khối Block size: kích thước càng lớn sẽ
càng an toàn
– Kích thước khoá Key size: kích thước càng lớn sẽ
càng an toàn (không gian khoá lớn)
– Số vòng (number of round): càng nhiều vòng lặp, độ
phức tạp và tính an toàn càng cao.
– Mode mã hoá (Encryption modes): xác định phương
thức phân chia thông điệp lớn thành các khối –
quan trọng đối với sự an toàn của thông điệp mật
68
Mật mã khối ( block cipher )
l Mật mã khối và các mật mã cơ sở khác
– Mật mã khối có thể được sử dụng để xây dựng các mật mã cơ
sở khác (cryptographic primitives).
l Để cho các phương pháp mã hóa này trở thành mật mã an toàn,
những thuật toán này cần được xây dựng theo phương pháp đúng
đắn.
– Các mật mã dòng có thể được xây dựng dựa trên mật mã khối.
l Các chế độ OFB-mode và CTR mode là những chế độ theo khối.
l Cho phép chuyển một mật mã khối thành mật mã dòng.
– Mật mã khối có thể sử dụng để xây dựng các hàm băm, và
ngược lại, những hàm băm có thể là cơ sở để xây dựng những
mật mã khối.
l Ví dụ: những mật mã khối dựa trênhàm băm:SHACAL, BEAR và
LION.
69
Mật mã khối ( block cipher )
– Những bộ sinh số giả ngẫu nhiên an toàn theo phương
diện mật mã có thể được tạo nên từ các mật mã khối.
– Mã xác thực thông điệp (MAC) cũng thường được xây
dựng từ các mật mã khối. Ví dụ: CBC-MAC, OMAC,
PMAC.
– Các mã xác thực cũng được xây dựng từ mật mã khối.
l Cho phép thực hiện mã hóa mật và mã hóa xác thực đồng thời.
l Điều này làm cho phương pháp cung cấp được cả tính riêng tư
cũng như tính xác thực đồng thời. Ví dụ CCM, EAX, GCM,
OCB.
70
Mật mã khối ( block cipher )
l Thám mã khối
– Bên cạnh các phương pháp thám mã như thám mã tuyến tính,
thám mã vi phân, còn có một số phương pháp khác:
l Thám mã vi phân ngắn gọn ( Truncated differential cryptanalysis );
l Thám mã vi phân từng phần ( Partial differential cryptanalysis );
l Tấn công trượt ( Slide attacks );
l Tấn công Bu-mê-răng ( Boomerang attacks ),
l Tấn công toàn phương và tích phân,
l Tấn công XSL,
l Tấn công vi sai bất khả và
l Tấn công đại số
– Đối với mỗi mật mã khối mới được xây dựng, để có tính hiệu quả,
mật mã đó phải thể hiện độ an toàn đối với các tấn công đã biết.
71
Hệ mật hoàn hảo và không hoàn hảo
l Điều kiện cần để hệ mật
là hệ mật hoàn hảo X*
Thám mã
K*
Nguồn X Thuật toán Y Thuật toán X Nguồn
thông điệp mã hóa giải mã thông điệp
K Đối phương biết:
Kênh mật - Bản tin mật mã;
Nguồn tạo - Thuật tóan mật mã;
R Khóa
số ngẫu
mật - Thông tin về nguồn thông
72 nhiên điệp: thuộc tính thống
kê của bản rõ
Hệ mật hoàn hảo và không hoàn hảo
– Nguồn thông tin X = [ X1, X2, ..., XM ], Xi Î A; A –
bảng ký tự bản rõ cùng các thuộc tính thống kê (
latin, nhị phân, ...).
– Khoá K = [ K1, K2, ... KL ], khóa K được tạo ra.
l Các ký tự của khoá K nằm trong một bảng ký tự: bảng ký
tự nhị phân { 0, 1 }
– Bộ tạo số ngẫu nhiên: R = [ R1, R2, ..., RJ ];
– Thông điệp được mã hóa là hàm của X, R và K : Y
= [ Y1, Y2, ..., YN ]
Y = EKR( X )
– Bên nhận giải mã thông điệp bằng khóa đã phân
73 phối:
X =) DK( Y
Hệ mật hoàn hảo và không hoàn
hảo
– Giả thiết sử dụng khóa và tạo số ngẫu nhiên:
l Khóa mật chỉ được sử dụng một lần.
l M bit của văn bản rõ sẽ được mã hoá trước khi khoá mật K
và chuỗi ngẫu nhiên R thay đổi.
– Đối phương chỉ biết được văn bản mã mật Y và thuật
tóan mã hóa, giải mã.
– Sơ đồ hệ mật hoàn hảo: Văn bản rõ X độc lập thống
kê với văn bản mã mật Y.
P( X = x | Y = y ) = P( X = x )
đối với mọi bản tin rõ: X = [ x1, x2, ..., xM ] và bản tin
mật Y.
74
Hệ mật hoàn hảo và không hoàn
hảo
– Ví dụ: hệ mã Vernam
l Bảng chữ cái: A = { 0, 1, ..., |A|– 1 }
l Độ dài của văn bản gốc, khoá và văn bản mã bằng nhau:
M = L = N.
l Khoá được chọn ngẫu nhiên: P( K = k ) = |A|-M đối với
|A|M tổ hợp khoá.
l Quá trình mã hoá: Yi = Xi Å Ki, i = 1, 2, ..., M.
l Do với mỗi ký tự xj thuộc Xi và yi thuộc Yj ta có duy nhất
ki thuộc Kj, do đó: P( Y = y | X = x ) = P( Z = z ) = |A|-M
không phụ thuộc vào X.
75
Hệ mật hoàn hảo và không hoàn
hảo
– Định lý: đối với hệ mật hoàn hảo
H( X ) = H( X | Y ) £ H( K )
– Nếu bản rõ và bản mã cùng bảng ký tự, : LX = LK
l Khi dấu bằng xảy ra: trong trường hợp one time pad.
l Các hệ mật không hoàn hảo
– Đặt vấn đề: khi nào thám mã có thể phá được các
hệ mật không hoàn hảo ?!
76
Quản trị và phân phối khóa trong mã
hóa đối xứng
l Đặt vấn đề:
– Trong kỹ thuật mật mã truyền thống, hai phía tham gia
vào truyền tin phải chia sẻ khoá mật Þ khoá phải
được đảm bảo bí mật : phải duy trì được kênh mật
phân phối khóa.
– Khóa phải được sử dụng một lần: Khoá phải được
thường xuyên thay đổi.
– Mức độ an toàn của bất kỳ hệ mật sẽ phụ thuộc vào kỹ
thuật phân phối khoá.
77File đính kèm:
 bai_giang_nhap_mon_an_toan_thong_tin_chuong_ii_cac_phuong_ph.pdf
bai_giang_nhap_mon_an_toan_thong_tin_chuong_ii_cac_phuong_ph.pdf

