Bài giảng môn Vận hành và điều khiển hệ thống điện - Chương 4, Phần 3: Điều phối tối ưu công suất nhà máy nhiệt điện

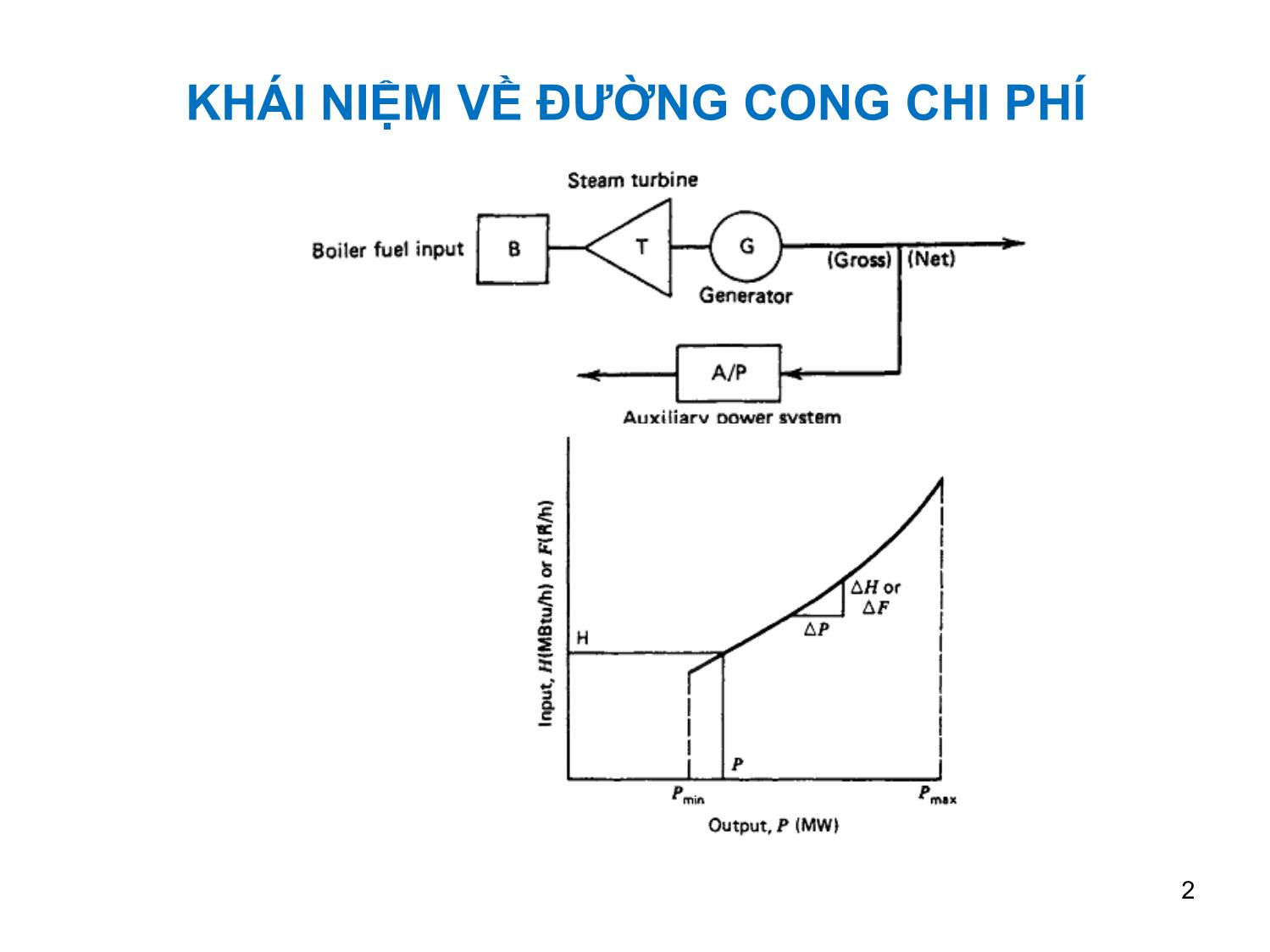
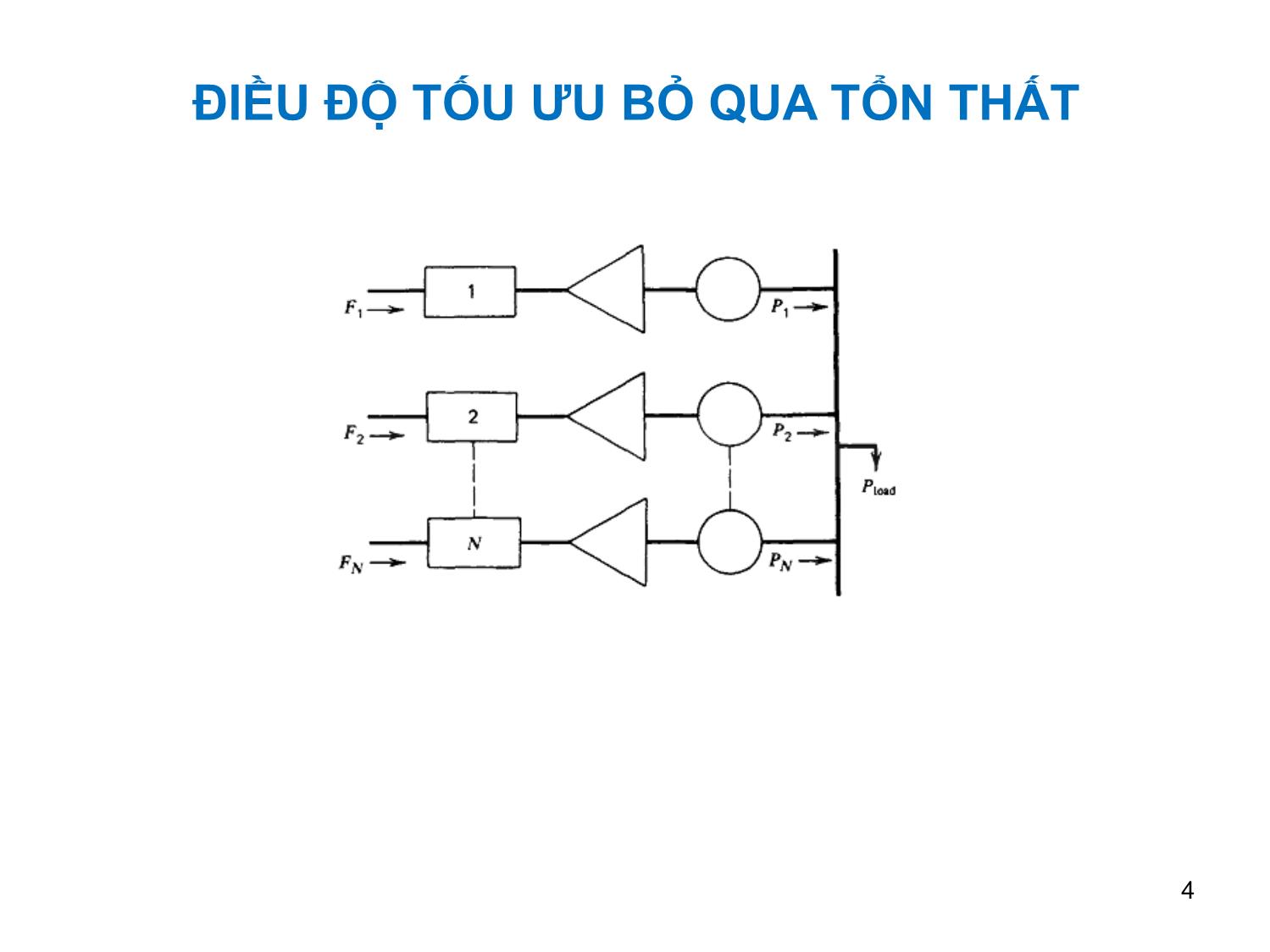
VẬN HÀNH VÀ ĐIỀU KHIỂN 
 HỆ THỐNG ĐIỆN
 Chương 4
Điều Phối Tối Ưu Công Suất Nhà 
 Máy Nhiệt Điện
KHÁI NIỆM VỀ ĐƯỜNG CONG CHI PHÍ
 2
KHÁI NIỆM VỀ ĐƯỜNG CONG CHI PHÍ
 Hàm chi phí có dạng:
 2
 Fi = aiPi +biPi+ci
 Suất chi phí: Fi/Pi
 Suất tăng chi phí: 
 dFi
 i2 a i P i b i
 dPi
 3
ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
 4
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
 Phát biểu bài toán
Hàm mục tiêu:
 NN
 2
 F Fi( a i P i b i P i c i ) m in (1)
 ii11
Thoả ràng buộc:
 N
 PP
 i lo a d (2)
 i 1
 (3)
 5
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
 Giải bằng phương pháp Hàm Lagrange:
 N
 LFPP()lo a d i
 i 1
 Nghiệm:
 L
 0 (4)
 Pi
 L
 0 (5)
 Từ (4), ta có
 L F i
 i (6)
 PPii
Phân phối theo nguyên lý suất tăng chi phí bằng nhau
 6
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
Từ (6) và (5):
 20ai P i b i (7)
 N
 PPi lo a d (8)
 i 1
 Giải (7): b
 i (9)
 Pi
 2 a i
 Để xác định λ, thay (9) vào (8) và biến đổi:
 N
 b i
 Plo a d
 2 a
 i 1 i (10)
 N 1
 i 1 2 a i
 7
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
Giải bằng phương pháp lặp:
Thay (9) vào (8):
 N b
 i P
 lo a d (11)
 i 1 2 a i
Pt (11) có dạng:
 (12)
 fP() lo a d
Khai triển Taylor vế trái (12):
 ()k
 df ()
 ()()kk(13)
 fP() lo a d
 d
 8
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
Từ (13):
 ()()kk
 ()k PP
 ()k N (14)
 df () 1
 2 a
 i 1 i
 d
Trong đó:
 N
 ()()kk
 PPPlo a d i (15)
 i 1
 9
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
 Giá trị mới của λ:
 (k 1 ) ( k )() ( k ) (16)
Điều kiện dừng:
 ()k
 P (17)
 10
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
Ví dụ 1:
 2
 FPP10,004 1 5,3 1 500
 2
 FPP20,006 2 5,5 2 400
 2
 FPP30,009 3 5,8 3 200
 PMWlo a d 800
 11
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
Phương pháp giải tích:
 5 .3 5 .5 5 .8
 800
 0,008 0,012 0,018
 8 , 5
 111
 0,008 0,012 0,018
 8 , 5 5 , 3
 P1 400
 2 0 , 0 0 4
 8 , 5 5 , 5
 P2 250
 2 0 , 0 0 6
 8 , 5 5 , 8
 P3 150
 2 0 , 0 0 9
 12
 ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
Phương pháp lặp:
 (1 ) 6
 6 5 , 3
 P1 8 7 , 5
 2 0 , 0 0 4
 6 5 , 5
 P2 4 1, 6 6 6 7
 2 0 , 0 0 6
 6 5 , 8
 P3 1 1,1 1 1 1
 2 0 , 0 0 9
 P 800 (87,5 41,6667 11,1111) 659,7222
 (1 ) 6 5 9 , 7 2 2 2
 2 , 5
 111
 2 0,004 2 0,006 2 0,009 13
ĐIỀU ĐỘ TỐU ƯU BỎ QUA TỔN THẤT
 ( 2 )
 6 2 , 5
 8 , 5 5 , 3
 P1 400
 2 0 , 0 0 4
 8 , 5 5 , 5
 P2 250
 2 0 , 0 0 6
 8 , 5 5 , 8
 P3 150
 2 0 , 0 0 9
 P 800 (400 250 150) 0
 14
ĐIỀU ĐỘ TỐi ƯU BỎ QUA TỔN THẤT, CÓ XÉT 
 ĐẾN GIỚI HẠN CÔNG SUẤT
 Phát biểu bài toán
 Hàm mục tiêu:
 NN
 2
 F Fi( a i P i b i P i c i ) m in (18)
 ii11
 Thoả ràng buộc:
 PPP
 im in i i m a x (19)
 N
 PPi lo a d (20)
 i 1
 15
ĐIỀU ĐỘ TỐi ƯU BỎ QUA TỔN THẤT, CÓ XÉT 
 ĐẾN GIỚI HẠN CÔNG SUẤT
 Tính chất lời giải:
 16
 ĐIỀU ĐỘ TỐi ƯU BỎ QUA TỔN THẤT, CÓ XÉT 
 ĐẾN GIỚI HẠN CÔNG SUẤT
Ví dụ 2:
 2
 FPP10,004 1 5,3 1 500
 2
 FPP20,006 2 5,5 2 400
 2
 FPP30,009 3 5,8 3 200
 2 0 0P1 4 5 0
 1 5 0P2 3 5 0
 1 0 0P3 2 2 5
 PMWlo a d 975
Giải bằng phương pháp lặp
 17
ĐIỀU ĐỘ TỐi ƯU BỎ QUA TỔN THẤT, CÓ XÉT 
 ĐẾN GIỚI HẠN CÔNG SUẤT
 (1 ) 6
 6 5 , 3
 P1 8 7 , 5
 2 0 , 0 0 4
 6 5 , 5
 P2 4 1, 6 6 6 7
 2 0 , 0 0 6
 6 5 , 8
 P3 1 1,1 1 1 1
 2 0 , 0 0 9
 P 975 (87,5 41,6667 11,1111) 834,7222
 (1 ) 8 3 4 , 7 2 2 2
 3,1 6 3 2
 111
 2 0,004 2 0,006 2 0,009
 18
ĐIỀU ĐỘ TỐi ƯU BỎ QUA TỔN THẤT, CÓ XÉT 
 ĐẾN GIỚI HẠN CÔNG SUẤT
 ( 2 ) 6 3,1632 9,1632
 9 ,1 6 3 2 5 , 3
 P1 4 8 2 , 8 9 4 7
 2 0 , 0 0 4
 9 ,1 6 3 2 5 , 5
 P2 3 0 5 , 2 5 3 2
 2 0 , 0 0 6
 9 ,1 6 3 2 5 , 8
 P3 1 8 6 , 8 4 2 1
 2 0 , 0 0 9
 PP1 1 m a x 450
 P1 450
 ( 2 )
 P 975 (450 250 150) 32,8947
 19
ĐIỀU ĐỘ TỐi ƯU BỎ QUA TỔN THẤT, CÓ XÉT 
 ĐẾN GIỚI HẠN CÔNG SUẤT
 ( 2 ) 3 2 , 8 9 4 7
 0 , 2 3 6 8
 11
 2 0,006 2 0,009
 ( 3 ) ( 2 ) ( 2 )
 9,1632 0,2368 9,4
 P1 450
 9 , 4 5 , 5
 P2 325
 2 0 , 0 0 6
 9 , 4 5 , 8
 P3 200
 2 0 , 0 0 9
 ( 3 )
 P 975 (450 325 200) 0
 20
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
 21
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Tổn thất có thể được biểu diễn dưới dạng hàm bậc 2
của công suất các máy phát (công thức tổn thất
Kron):
 NNN
 PPBPBPBlo s s i ij j0 i i 0 0 (21)
 i1 j 1 i 1
Các hệ số Bij được gọi là hệ số tổn thất hoặc hệ số B.
Hệ số B được xem là không đổi nếu chế độ vận hành
thực tế gần với chế độ sử dụng để xác định hệ số B.
 22
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Phát biểu bài toán
Hàm mục tiêu:
 NN
 2
 F Fi( a i P i b i P i c i ) m in (22)
 ii11
Thoả ràng buộc:
 N
 PPPi lo a d lo s s (23)
 i 1
 PPPim in i i m a x (24)
 23
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Hàm Lagrange mở rộng
 N
 LFPPP()lo a d lo s s i
 i 1 (25)
 NN
 imax()()PPPP i i max i min i min i
 ii11
 μ = 0 nếu P < P
 imax i imax (26)
 μimin = 0 nếu Pi > Pimin
 24
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
 Nghiệm tối ưu thỏa :
 L d F P
 i( 0 lo s s 1) 0 (27)
 Pi d P i P i
 N
 L (28)
 PPPlo a d lo s s i 0
 i 1
 L
 PP 0
 iim a x (29)
 i m a x
 L
 PPiim in 0 (30)
 i m in
Hai pt cuối chỉ tồn tại khi CS máy phát vượt quá giới hạn
 25
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Nếu CS máy phát nằm trong giới hạn, từ (27):
 1 dF
 i (31)
 P dP
 1 lo s s i
 P
P i
 lo s s được xác định từ (21):
 Pi
 N
 Plo s s
 2 BPBij j0 i (32)
 Pi i 1
dF
 i được biểu diễn
dPi
 dFi
 2 abii (33)
 dPi
 26
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Thay (33) và (32) vào (31):
 N
 22ai P i b i B ij P j B 0 i (34)
 j 1
Pt (34) được viết lại thành
 N
 abii1
 (BPBPBii ) i ij j (10 i ) (35)
 j 0 2
 ji
 27
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Khai triển (35), dưới dạng ma trận/ vec tơ, ta có:
ab11
 BBBB1 1 1 2 1N 1 0 1
 P1
 ab
 22P
 BBBB2 1 2 2 2N 2 1 1 0 2
  2
     
 PN
 abNN
 BBBBNNNNN1 2 1 0
 (36)
Với giá trị ước lượng của λ, giá trị tối ưu của Pi được
xác định từ việc giải hệ phương trình trên
 28
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Quá trình lặp:
Công suất nhà máy i ở bước lặp k được xác định từ (35):
 N
 ()()()k k k
 (1B0 i ) b i 2 B ij P j
 i 1
 ij
 P ()k (37)
 i ()k
 2 (aBi ii )
Thay (37) vào (23): N
 ()()()k k k
 (1B0 i ) b i 2 B ij P j
 N i 1
 ij
 PP()k (38)
 ()k lo a d lo s s
 i 1 2 (aBi ii )
 29
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Khai triển Taylor vế trái (38), ta có:
 ()k
 df ()
 ()()()k k k (39)
 f() Plo a d P lo s s
 d
 ()()kk
 ()k PP
 ()()kkN (40)
 d f() d Pi
 d d
Ở đây: i 1
 N
 ()()()k k k
 PPPPlo a d lo s s i (41)
 i 1
 N
 ()k
 ai(1 B0 i ) B ii b i 2 a i B ij P j
 ()k i 1
 N dP
 i ij (42)
 (k ) 2
 i 1 d2 ( ai B ii ) 30
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Cập nhật giá trị mới của λ:
 (k 1) ( k ) ( k ) (43)
Quá trình được tiếp tục cho tới khi
 ()k
 P (44)
 31
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Quá trình lặp được tóm tắt như sau:
•Bước 1: Cho giá trị ban đầu của λ
•Bước 2: Giải hệ (36) để tìm Pi, i = 1, , N
•Bước 3: Tính ΔP từ (41).
 Nếu | ΔP | < ε, đến bước 5;
 N dP
 Ngược lại, tính i từ (42) và Δλ từ (40).
 i 1 d
•Bước 4: Tính giá trị mới của λ từ (43), trở về bước 2
•Bước 5: Dừng
 32
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Trong trường hợp đặc biệt, tổn thất công suất tác dụng
có dạng:
 N
 2 (45)
 PBPlo s s ij i
 i 1
Các phương trình sửa dụng cho các bước lặp trở thành:
 ()k
 ()k bB
 P i ii (46)
 i ()k
 2 (a i )
 ()k
 N d P a B b
 i i ii i (47)
 (k ) 2
 i 1 d2 ( ai B ii )
 33
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Ví dụ 3:
 2
 FPP10 , 0 0 8 1 7 1 2 0 0
 2
 FPP20,009 2 6,3 2 180
 2
 FPP30,007 3 6,8 3 140
 1 0P1 8 5
 1 0P2 8 0
 1 0P1 7 0
 PMWlo a d 150
 2 2 2
 PPPPlo s s 0,0002181 0,000228 2 0,000179 3
 34
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Chọn λ(1) = 8:
 (1 ) 87
 P1 5 1, 3 1 3 6
 2(0,008 8 0,000128)
 (1 ) 8 6 , 3
 P2 7 8 , 5 2 9 2
 2(0,009 8 0,000228)
 (1 ) 8 6 , 8
 P3 7 1,1 5 7 5
 2(0,007 8 0,000179)
 (1 ) 2 2
 Plo s s 0,000128(51,3136) 0,000228(78,5292)
 2
 0,000179(71,1575) 2,8864
 35
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
 (1 )
 P 150 2,8864 (51,3136 78,5292 71,1575)
 4 8 ,1 1 3 9
 (1 )
3
 Pi 0,008 0,000128 7
 2
i 1 2(0,008 8 0,000218)
 0,009 0,000228 6,3
 2(0,009 8 0,000228) 2
 0,007 0,000179 6,8
 2(0,007 8 0,000179) 2
 1 5 2 , 4 9 2 4
 (1 ) 4 8 ,1 1 3 9
 0 , 3 1 5 5
 1 5 2 , 4 9 2 4 36
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Giá trị mới của λ:
 ( 2 ) (1 ) (1 ) 8 0,3155 7,6845
Quá trình lặp được tiếp tục với kết quả như sau:
 ( 2 )
 P1 3 5 , 3 7 2 8
 ( 2 )
 P2 6 4 , 3 7 2 8
 ( 2 )
 P3 5 2 , 8 0 1 5
 ( 2 )
 Plo s s 1, 7 1 7
 ( 2 )
 P 0 , 8 3 9 5
 ( 2 )
 3 P
 i 1 5 4 , 5 8 8
 i 1
 ( 2 ) 37
 0 , 0 0 5 4 3 1
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
 ( 3 )
 7 , 6 7 9
 ( 3 )
 P1 3 5 , 0 9 6 5
 ( 3 )
 P2 6 4 ,1 3 6 9
 ( 3 )
 P3 5 2 , 4 8 3 4
 ( 3 )
 Plo s s 1, 6 9 9
 ( 3 )
 P 0 , 0 1 7 4 2
 ( 3 )
 3 P
 i 1 5 4 , 6 2 4
 i 1
 ( 3 )
 0 , 0 0 0 1 1 2 7
 38
 ĐIỀU ĐỘ TỐI ƯU CÓ XÉT TỔN THẤT
Quá trình lặp được kết thúc ở bước 4 với |ΔP(4)|< 10-3,
kết quả như sau:
 ( 4 )
 7 , 6 7 8 9
 ( 4 )
 P1 3 5 , 0 9 0 7
 ( 4 )
 P2 6 4 ,1 3 1 7
 ( 4 )
 P3 5 2 , 4 7 6 7
 ( 4 )
 Plo s s 1, 6 9 9
 39
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT CẤU TRÚC MẠNG ĐIỆN
 1 N+1 Pload1
 F1
 P1
 2 N+2 Pload2
 F2
 P
 2 Power system 
 network
 N N+M PloadM
 FN
 PN
 40
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT CẤU TRÚC MẠNG ĐIỆN
 Phát biểu bài toán
 Hàm mục tiêu:
 NN
 2
 F Fi( a i P i b i P i c i ) m in (48)
 ii11
 Thoả ràng buộc:
 •Nút máy phát (kể cả nút cân bằng):
 P() i P
 b u s i (49)
 V() i V
 b u s g i (50)
 iN1, ...,
 (bỏ qua giới hạn công suất phản kháng)
 41
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT CẤU TRÚC MẠNG ĐIỆN
 •Nút tải:
 Pb u s() N i P lo a d i (51)
 Qb u s() N i Q lo a d i (52)
 iM1, ...,
 Trong (49) – (52):
 *
 Pbus()Re i V bus () i Y bus (,) i k V bus () k (53)
 k
 *
 Qbus()Im i V bus () i Y bus (,) i k V bus () k (54)
 k
 i1, ..., ( N M )
 42
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT CẤU TRÚC MẠNG ĐIỆN
 Trong (53) và(54):
 Re (.) và Im(.) là phần thực và phần ảo của biểu 
 thức trong dấu ngoặc
 (.)* là liên hợp của biểu thức trong dấu ngoặc
 Ybus là ma trận tổng dẫn nút của mạng điện
 Bài toán này được giải bằng chương trình Matlab, 
 sử dụng hàm fmincon
 43
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT CẤU TRÚC MẠNG ĐIỆN
 Ví dụ 4: Tính toán điều độ tối ưu cho HTĐ có 
 các thông số và sơ đồ được cho như sau:
 Thông số nhánh
 Nút 1 Nút 2 R(pu) X (pu) B (pu)
 1 2 0.0168 0.0650 0.1760
 2 4 0.0134 0.0520 0.1408
 4 3 0.0118 0.0455 0.1232
 4 5 0.0101 0.0390 0.1056
 3 5 0.0101 0.0390 0.1056
 5 6 0.0101 0.0390 0.1056
 1 6 0.0084 0.0325 0.0880
 44
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT CẤU TRÚC MẠNG ĐIỆN
 Thông số tải
 Nút P(MW) Q (MVAr)
 4 400 131,47
 5 400 131,47
 6 300 98,60
 Thông số máy phát Hàm chi phí
 2
 Nút V(pu) F1= 0,008P1 +7P1 +200
 2
 1 1,05 F2= 0,009P2 +6,3P2 +180
 2
 2 1,02 F3= 0,007P3 +6,8P3 +140
 3 1,03
 45
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT CẤU TRÚC MẠNG ĐIỆN
 400.0 MW
 131.47 MVAr
 1 2 4
 6 5 3
 300.0 MW 400.0 MW
 98.60 MVAr 131.47 MVAr
 46
ĐIỀU ĐỘ TỐI ƯU CÓ XÉT CẤU TRÚC MẠNG ĐIỆN
 Bài toán trên dược giải bằng chương trình 
 Matlab
 47