Bài giảng môn Trường điện từ - Chương 4: Trường điện từ biến thiên
1. Khái niệm chung
2. Các phương trình TĐTBT dạng phức
3. Sóng ĐTPĐS truyền trong MTĐM lý tưởng
4. Sóng ĐTPĐS truyền trong MTVD lý tưởng
5. Bức xạ điện từ
Từ hệ PT trên cho thấy TĐTBT vừa có tính
chất xoáy vừa có tính chất thế, do đó có thể
khảo sát trường bằng hàm thế vectơ và thế vô
hướng.

Trang 1

Trang 2

Trang 3

Trang 4
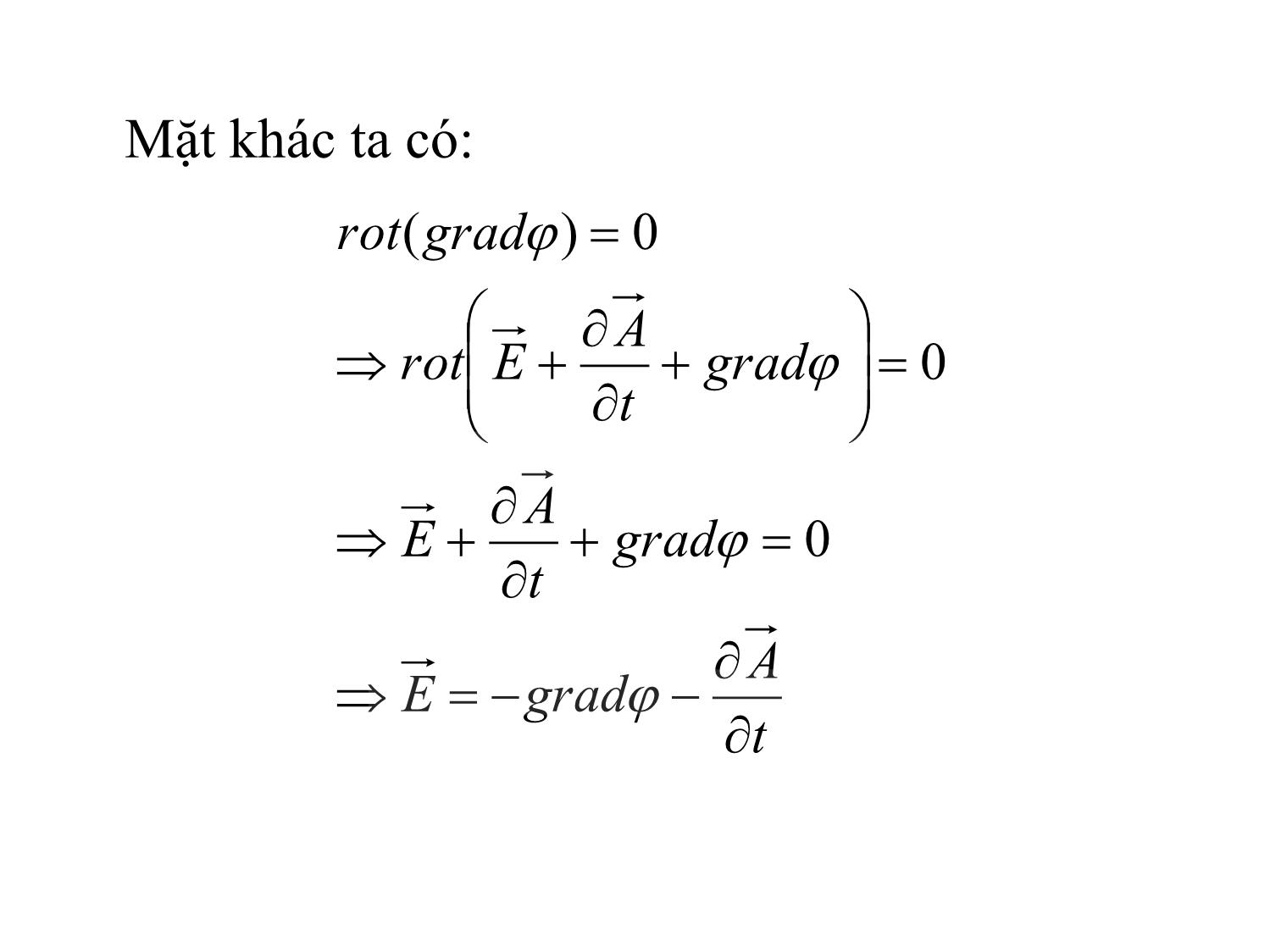
Trang 5

Trang 6
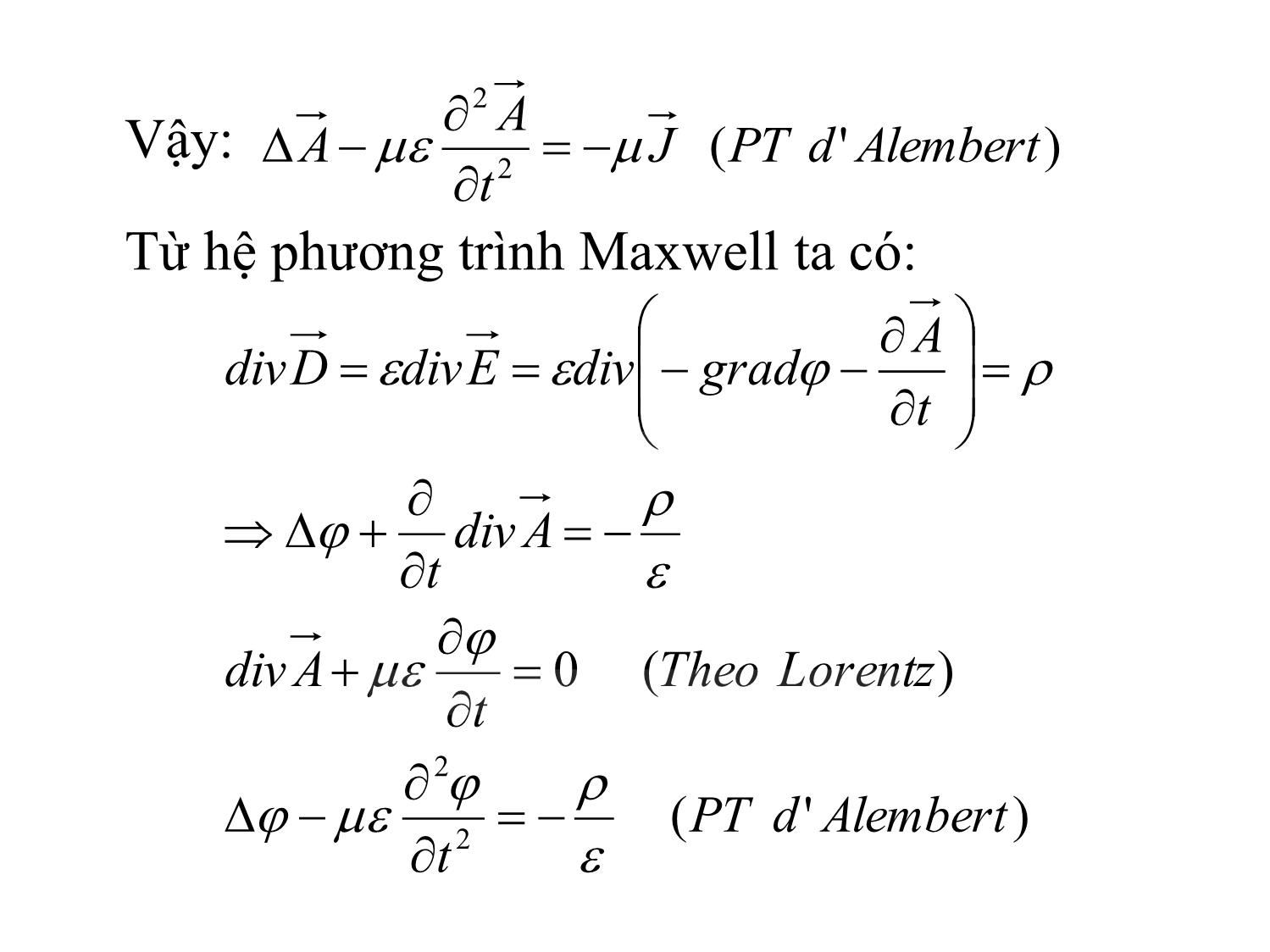
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng môn Trường điện từ - Chương 4: Trường điện từ biến thiên", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng môn Trường điện từ - Chương 4: Trường điện từ biến thiên

CHƢƠNG 4 TRƢỜNG ĐIỆN TỪ BIẾN THIÊN CHƢƠNG 4: TĐT BIẾN THIÊN 1. Khái niệm chung 2. Các phƣơng trình TĐTBT dạng phức 3. Sóng ĐTPĐS truyền trong MTĐM lý tƣởng 4. Sóng ĐTPĐS truyền trong MTVD lý tƣởng 5. Bức xạ điện từ 1. Khái niệm chung TĐTBT được mô tả bởi hệ PT Maxwell 0 Bdiv Ddiv t B Erot t D JHrot Từ hệ PT trên cho thấy TĐTBT vừa có tính chất xoáy vừa có tính chất thế, do đó có thể khảo sát trường bằng hàm thế vectơ và thế vô hướng. Gọi là thế vectơ, ta có: Mà: A ArotB 0 t A Erot t A rotArot tt B Erot Mặt khác ta có: t A gradE grad t A E grad t A Erot gradrot 0 0 0)( Mà ta có: Vậy: Từ hệ phương trình Maxwell ta có: )'( 2 2 AlembertdPTJ t A A )'( )(0 2 2 AlembertdPT t LorentzTheo t Adiv Adiv t t A graddivEdivDdiv Như vậy ta được hệ PT truyền sóng d’Alembert Nếu MT không chứa dòng điện và điện tích thì: 2 2 2 2 t J t A A 0 0 2 2 2 2 t t A A Tương tự trong MTĐM lý tưởng, đối với E và H ta cũng có: 0 0 2 2 2 2 t H H t E E 2. Các PT TĐTBT dạng phức Biểu diễn phức quá trình điều hòa: zyxEe eEieEieEie zyxtzyxEi zyxtzyxEi zyxtzyxEitzyxE tj j zmz j ymy j xmx tj zzmz yymy xxmx zyx ,,.Re ...Re ),,(cos),,( ),,(cos),,( ),,(cos),,(),,,( Vậy ta được: zyxEtzyxE t zyxEjtzyxE t zyxEtzyxE ,,),,,( ,,),,,( ,,),,,( 2 2 2 Hệ phương trình Maxwell dạng phức: 0 Bdiv Ddiv BjErot DjJHrot Hệ phương trình sóng dạng phức: j JAA ~ ~ ~ ~ 2 2 Hệ phương trình sóng dạng phức: 0~ 0~ 2 2 AA 0~ 0~ 2 2 HH EE 3. Sóng ĐTPĐS trong MTĐM lý tƣởng Xét sự lan truyền của sóng phẳng như hình vẽ: Phương trình truyền sóng có dạng: ; 0xE E x y 22 2 2 2 x x d Ed E E dz dz 0 ~ const const Đặt: Nghiệm PT trên có dạng: Cường độ từ trường H: jjjK K 22 KzAKzAiE x exp.exp. 21 KzA j K KzA j K iH y exp.exp. 21 Vậy : Tổng trở sóng: Xét thành phần sóng thuận: HHiH EEiE y x K j H E H E ZC zt Z A H ztAE Kz Z A H KzAE C C cos.2 cos.2 exp. exp. 1 1 1 1 Hình ảnh lan truyền của sóng thuận: Từ kết quả trên cho thấy: Sóng lan truyền trong MTĐM lý tưởng không bị tắt dần Góc: pha: Hệ số pha: Vận tốc pha: Bước sóng: Tổng trở sóng: Sóng E và H vuông góc nhau. 0 0 1 r r r r c v zt 2 . f v Tv K j H E H E ZC 4. Sóng ĐTPĐS trong MTVD lý tƣởng Xét sự lan truyền của sóng phẳng như hình vẽ: Phương trình truyền sóng có dạng: ; 0xE E x y 0 ~ const j x x Ej dz Ed dz Ed 2 2 2 2 Đặt: Nghiệm PT trên có dạng: Cường độ từ trường H: KzAKzAiE x exp.exp. 21 KzA j K KzA j K iH y exp.exp. 21 jjK jjKjK 22 2 12 Vậy : Tổng trở sóng: HHiH EEiE y x 045 j j j K j H E H E ZC Xét thành phần sóng thuận: 4 cos.2 cos.2 exp.exp. exp.exp. 1 1 11 11 zte Z A H zteAE zjz Z A Kz Z A H zjzAKzAE z C z CC Hình ảnh lan truyền của sóng thuận: Từ kết quả trên cho thấy: Góc: pha: Hệ số pha: Vận tốc pha: Bước sóng: Tổng trở sóng: zt 282 . f v Tv 2 2 v 045 H E H E ZC Độ sâu xuyên thấu (Z0): là khoảng cách tính từ mặt môi trường dẫn theo phương truyền sóng trên đó sóng giảm đi e lần. Ta có: Sóng E và H vuông góc nhau và cùng vuông góc với phương truyền sóng. 0 1 2 2 z 5. Bức xạ điện từ Khái niệm: TĐTBT có khả năng lan truyền trong không gian dưới dạng sóng từ những vùng có điện tích hoặc dòng điện biến thiên được coi là những nguồn. Đó là hiện tượng bức xạ điện từ Khi lan truyền, nó mang theo năng lượng, tín hiệu. Các TB dùng để bức xạ và thu SĐT gọi là anten Bức xạ điện từ của nguyên tố anten thẳng Nguyên tố anten (bức xạ) thẳng là một đoạn dây dẫn thẳng, hở 2 đầu, mang dòng điện biến thiên theo thời gian, có độ dài l đủ nhỏ so với bước sóng sao cho tại một thời điểm nhất định có thể coi dòng điện có giá trị như nhau trên toàn bộ đoạn dây. Xét trường bức xạ do dòng điện gây ra trong môi trường điện môi lý tưởng )sin( tIi m Hàm từ thế vectơ A có dạng: Nghiệm của phương trình này ở những vùng xa so với chiều dài của nguyên tố anten thẳng, R >> l có dạng: Với: J t A v A t A A 2 2 22 2 1 )sin( 4 .. )( 4 . )( 4 )( 4 kRt R Il v R ti R l dl v R ti R dv v R tJ R A m lV 2 v k Biểu diễn A bằng ảnh phức có dạng: với Sử dụng hệ tọa độ cầu với trục z hướng theo đoạn dây l thì từ thế vectơ A chỉ có 2 thành phần: Cường độ từ trường H có dạng: Ie A A= , 4 jkR R II= 2 im e jkR -jkR 0 Icos A Acos 4 Isin e A Asin 4 R l e R l R jkRR e RkkR j lk IA AR RR H 22 2 1sin 4 11 Cường độ điện trường E có 2 thành phần: Xét miền gần: 3322 3 1 2 cos sin sin 11 RkRk j e j lkI H Rj E jkRR 3322 3 11 4 sin11 RkRk j kR e j lkI RH RRj E jkR 1, 11 2 1 3322 jkRe RkRkRkR R 332 4 sin ; 2 cos ; 4 sin Rj lI E Rj lI E R lI H R Xét miền xa: 3322 11 2 1 RkRkRkR R 0 . 2 sin 4 sin 4 sin 2 sin 4 sin 4 sin 2 2 R C jkR C jkRjkR jkR jkRjkR E HZe R lI jZ e Rv lI je R lkI jE e R lI j e Rv lI je R lkI jH Chuyển sang giá trị tức thời: Véctơ Poynting: Công suất trường bức xạ: Tổng trở bức xạ: iR v t R lI ZE iR v t R lI H m C m 0 0 90sin 2 sin 90sin 2 sin HEP 2 2 2 2 3 2 3 1 . l IZ l IZSdPP CmC S bx 2 2 3 2 l Z I P R C bx bx
File đính kèm:
 bai_giang_mon_truong_dien_tu_chuong_4_truong_dien_tu_bien_th.pdf
bai_giang_mon_truong_dien_tu_chuong_4_truong_dien_tu_bien_th.pdf

