Bài giảng Mô hình hóa nhận dạng và mô phỏng - Chương 2: Mô hình hóa
Cô lập hệ thống - Liên kết ngoài
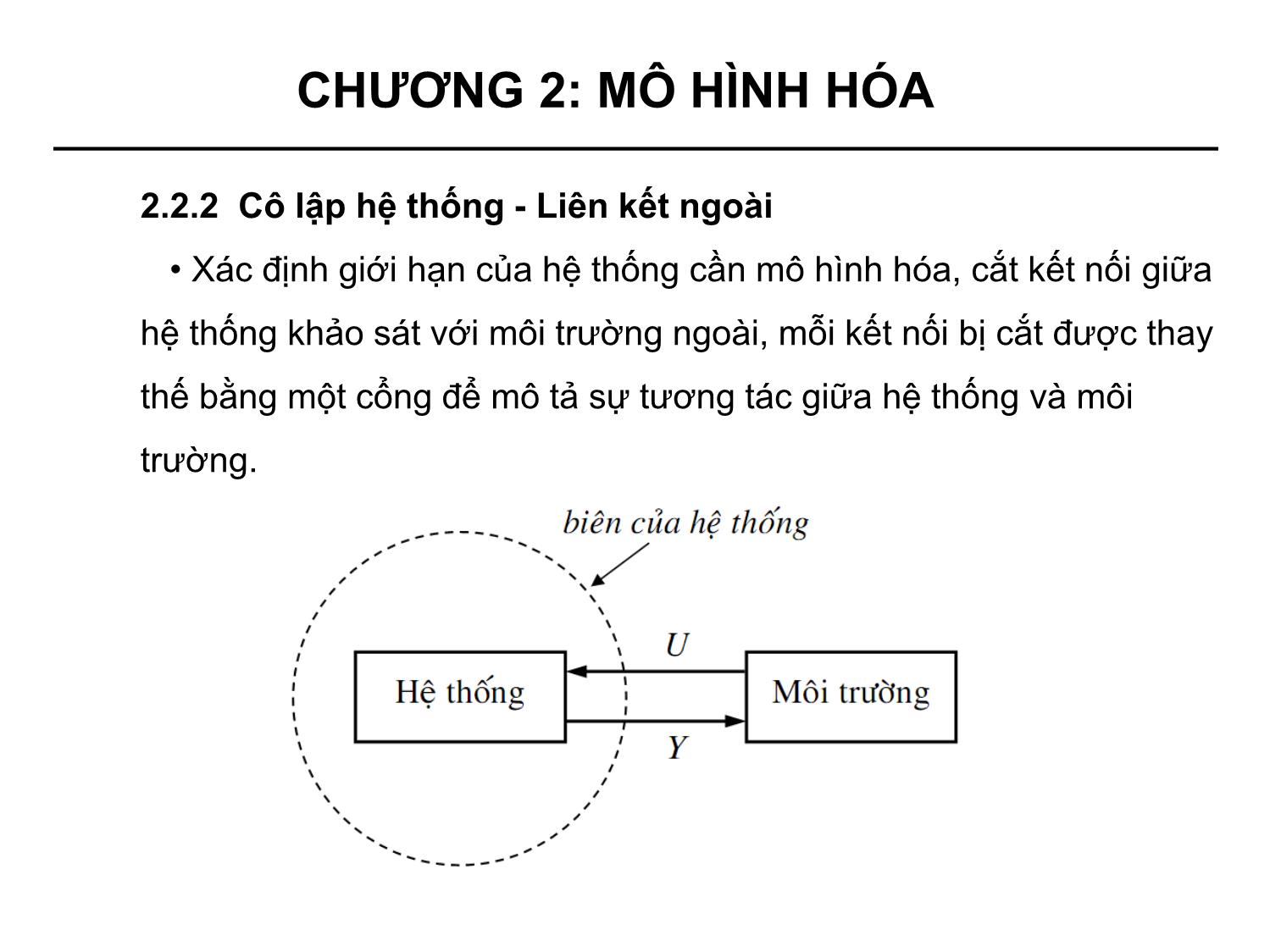
• Xác định giới hạn của hệ thống cần mô hình hóa, cắt kết nối giữa
hệ thống khảo sát với môi trường ngoài, mỗi kết nối bị cắt được thay
thế bằng một cổng để mô tả sự tương tác giữa hệ thống và môi
trường.
• Cổng (port): là một cặp đầu cuối mà qua đó năng lượng hoặc
công suất vào hoặc ra khỏi hệ thống.
Một hệ thống có thể có nhiều cổng (multiport system).
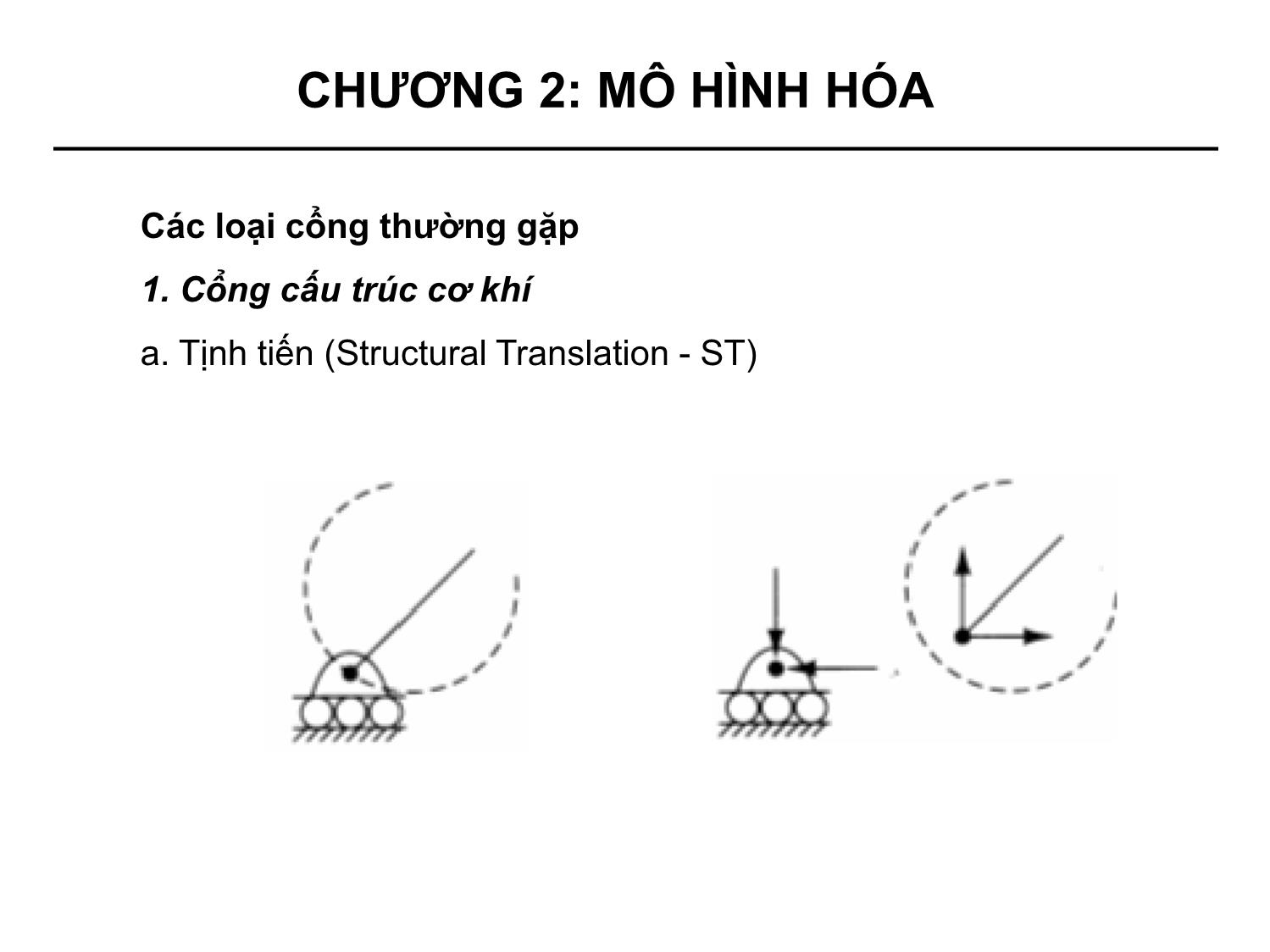
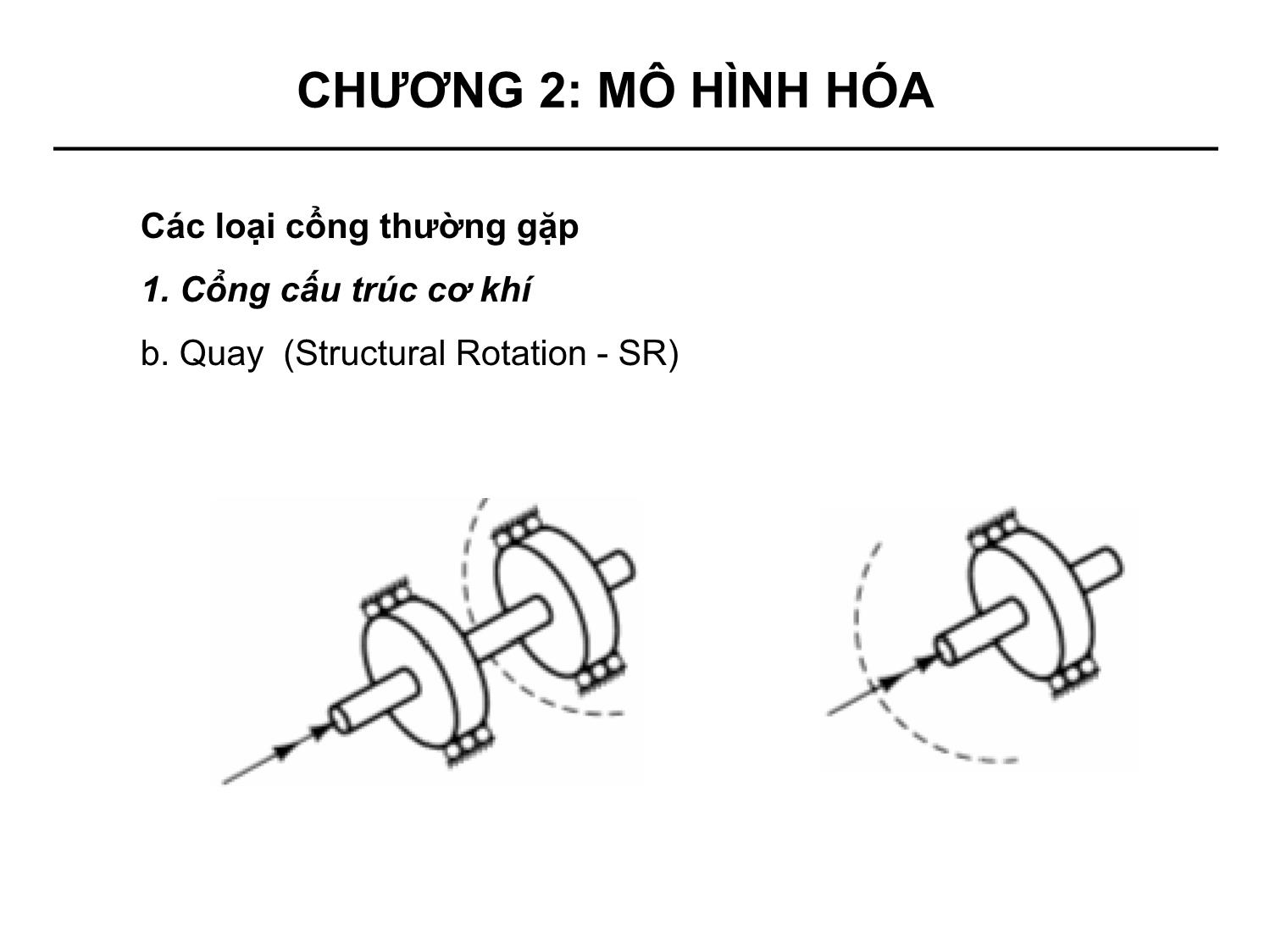
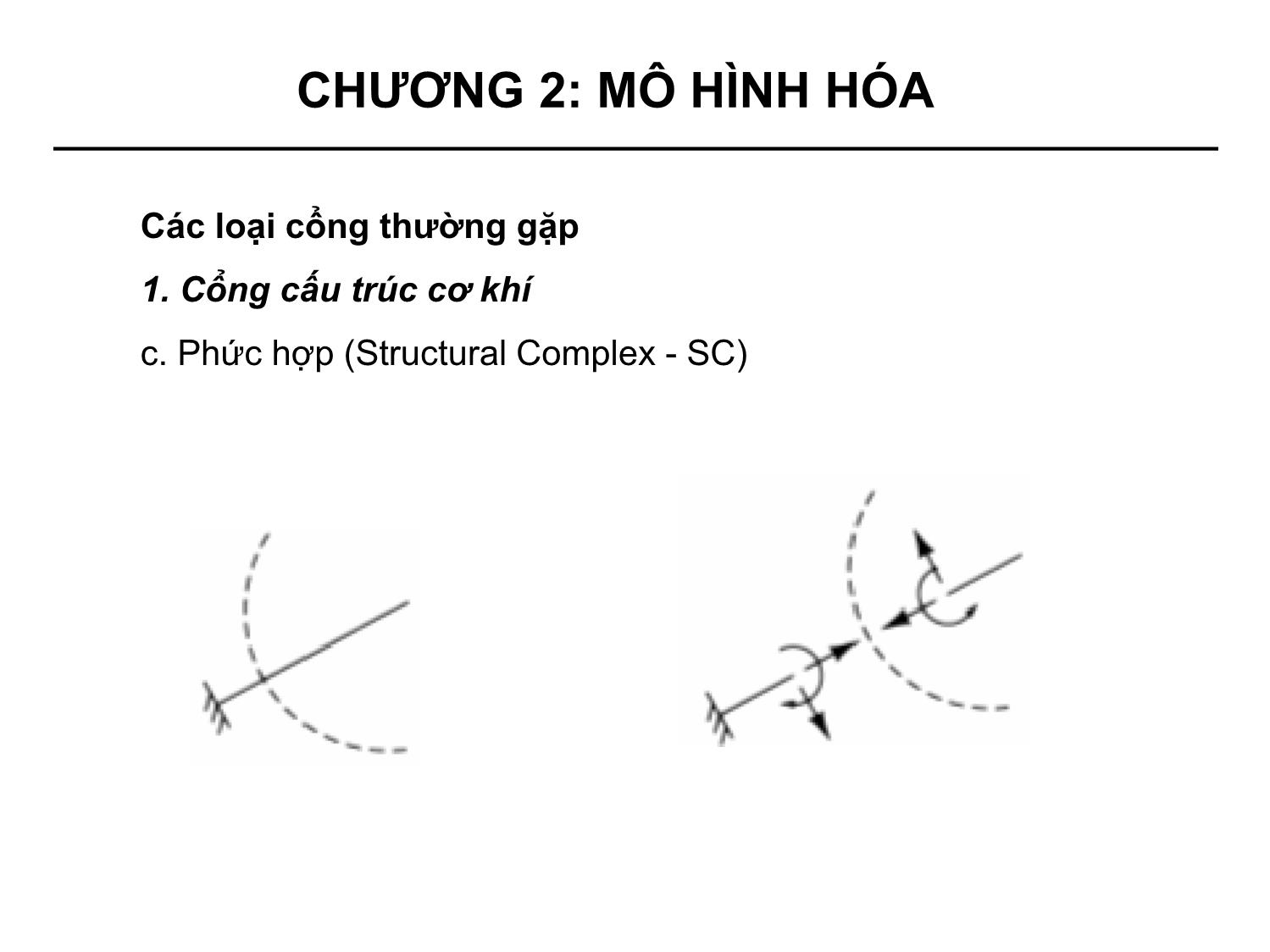
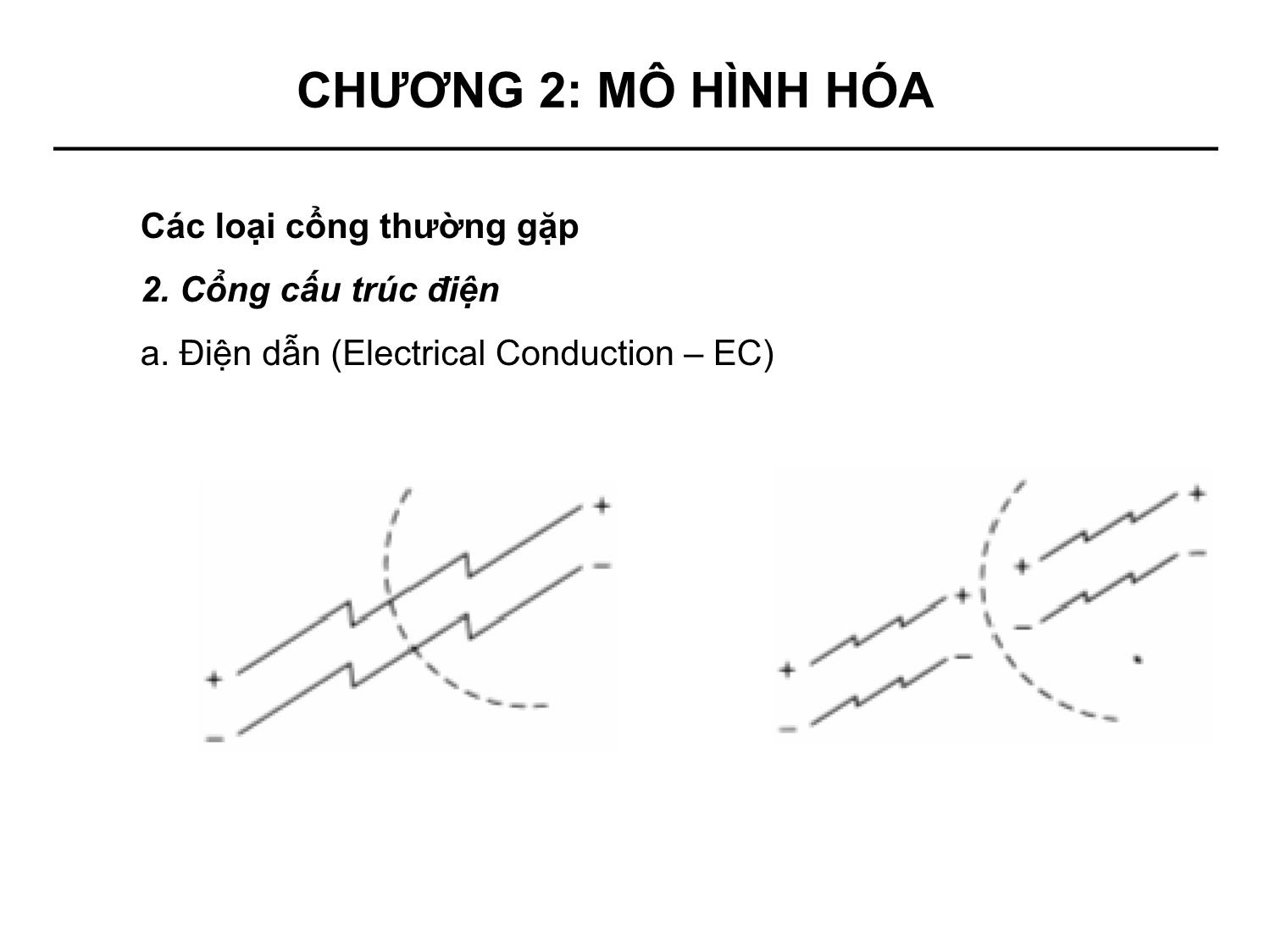
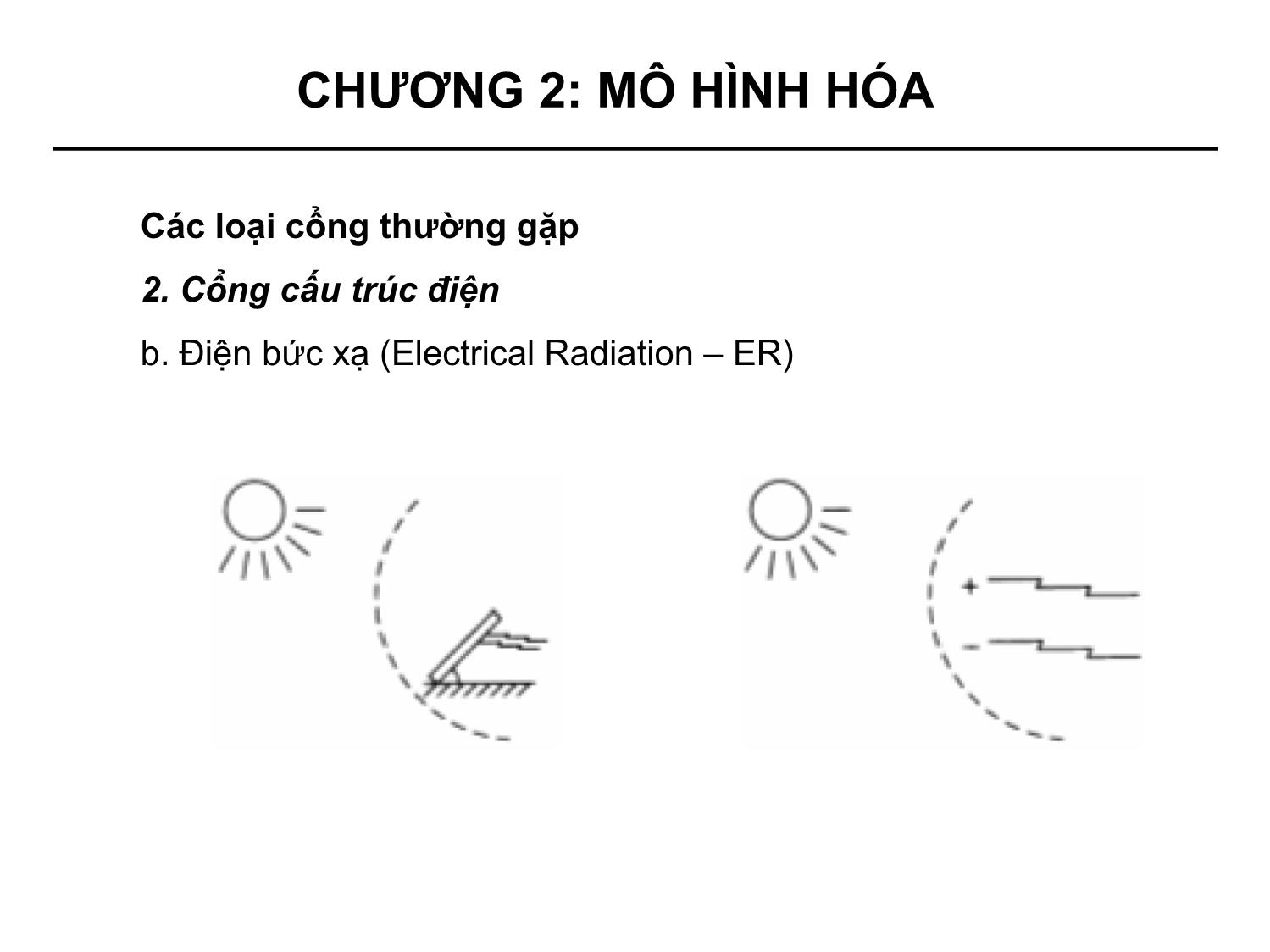
• Bốn loại cổng thường gặp:
+ Cơ khí (Structural)
+ Điện (Electrical)
+ Nhiệt (thermal)
+ Lưu chất (fluid)

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5
Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Mô hình hóa nhận dạng và mô phỏng - Chương 2: Mô hình hóa", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Mô hình hóa nhận dạng và mô phỏng - Chương 2: Mô hình hóa

I dt dH IT CHƯƠNG 2: MÔ HÌNH HÓA Nhiệt trở truyền nhiệt: CHƯƠNG 2: MÔ HÌNH HÓA Nhiệt trở truyền nhiệt: CHƯƠNG 2: MÔ HÌNH HÓA hRV 12 Nhiệt trở đối lưu: CHƯƠNG 2: MÔ HÌNH HÓA Nhiệt trở bức xạ: hRR 12 CHƯƠNG 2: MÔ HÌNH HÓA 2.3.5 Phân tích vật lý hệ lưu chất lỏng a. Các phần tử lưu chất Các biến trong hệ lưu chất : • Áp suất: p [N/m2] • Thể tích: V [m3] • Lưu lượng: q [m3/sec] dt dV q CHƯƠNG 2: MÔ HÌNH HÓA Các phần tử hệ lưu chất : • Lưu trở: Lưu trở của đường ống: [N.sec/m] Lưu trở đường ống còn tính theo: Công thức trên chỉ đúng trong trường hợp lưu chất chảy tầng (có hướng), và đường ống dẫn lưu chất dài (l > 20d) 4 128 d l RL q p RL CHƯƠNG 2: MÔ HÌNH HÓA • Lưu trở: Lưu trở của van: phi tuyến CHƯƠNG 2: MÔ HÌNH HÓA • Lưu trở: Lưu trở của van: phi tuyến CHƯƠNG 2: MÔ HÌNH HÓA • Lưu trở: Lưu trở của van: phi tuyến CHƯƠNG 2: MÔ HÌNH HÓA • Dung: pg A CL p V CL qdt C p L 1 CHƯƠNG 2: MÔ HÌNH HÓA • Dung: CHƯƠNG 2: MÔ HÌNH HÓA • Dung: CHƯƠNG 2: MÔ HÌNH HÓA • Quán tính: a l IL dt dq Ip L CHƯƠNG 2: MÔ HÌNH HÓA 2.3.6 Một số ví dụ: Ví dụ 2.5: Mô hình hóa hệ thống sau: Cách 1: Dùng định luật Newton Chiếu lên phương chuyển động, áp dụng định luật II Newton: sin)()( PtFtxm CHƯƠNG 2: MÔ HÌNH HÓA Cách 2: Dùng công thức Euler–Lagrange: Động năng: Thế năng: Áp dụng công thức Euler–Lagrange: 2 2 1 xmT sinmgxU sin 2 1 2 mgxxmUTL Fmgxm dt d F x L x L dt d sin)( Fmgxm sin CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.6: Mô hình hóa hệ thống giảm sốc của xe máy : Cách 1: Dùng định luật Newton )()()()( txbtkxtftxm )()()()( tftkxtxbtxm CHƯƠNG 2: MÔ HÌNH HÓA Cách 2: Áp dụng công thức Euler-Lagrange: Động năng: Thế năng: 2 2 1 xmT 2 2 1 kxU 22 2 1 2 1 kxxmUTL xbf x L x L dt d xbfkxxm dt d )( )()()()( tftkxtxbtxm CHƯƠNG 2: MÔ HÌNH HÓA Cách 3: Áp dụng sự tương đồng giữa hệ thống điện và hệ thống cơ: Thế: f ↔ U Lượng: x ↔ q Dung: 1/k ↔ C Trở: b ↔ R Cảm: m ↔ L CHƯƠNG 2: MÔ HÌNH HÓA Cách 3: Áp dụng sự tương đồng giữa hệ thống điện và hệ thống cơ: Quan hệ giữa dòng và áp của mạch điện tương: )( 1 )( sULs Cs RsI )( 1)( 2 sULs C Rs s sI )( 1 )( 2 sULs C RssQ )()( 1 )()( tutq C tqRtqL )()()()( tftkxtxbtxm CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.7: Mô hình hóa hệ con lắc ngược Trong đó: M : trọng lượng xe [Kg] m : trọng lượng con lắc [Kg] l : chiều dài con lắc [m] u : lực tác động vào xe [N] g : gia tốc trọng trường [m/s2] x : vị trí xe [m] θ : góc giữa con lắc và phương thẳng đứng [rad] CHƯƠNG 2: MÔ HÌNH HÓA Cách 1: Dùng định luật Newton Gọi (xP, yP) là tọa độ của vật nặng m ở đầu con lắc, ta có: Áp dụng định luật II Newton cho chuyển động theo phương x, ta có: Thay xP vào: cos sin ly lxx P P F dt xd m dt xd M P 2 2 2 2 Flx dt d m dt xd M )sin( 2 2 2 2 CHƯƠNG 2: MÔ HÌNH HÓA Triển khai đạo hàm: Áp dụng định luật II Newton cho chuyển động quay của con lắc quanh trục ta được: Thay xP và yP vào: Khai triển các đạo hàm và rút gọn ta được: sinsincos 2 2 2 2 mgll dt yd ml dt xd m PP FmlmlxmM )(cos)(sin)( 2 sinsin)cos(cos)sin( 2 2 2 2 mglll dt d mllx dt d m sincos mgmlxm CHƯƠNG 2: MÔ HÌNH HÓA Kết hợp hai phương trình: Ta được: FmlmlxmM )(cos)(sin)( 2 sincos mgmlxm 2 2 )(cos sincos)(sin mmM mgmlF x lmMml mlgmMF )()(cos )sin(cos)(sin)(cos 2 2 CHƯƠNG 2: MÔ HÌNH HÓA Cách 2: Dùng công thức Euler–Lagrange Gọi (xP, yP) là tọa độ của vật nặng m ở đầu con lắc, ta có: Động năng của vật nặng đầu con lắc: Động năng của xe: cos sin ly lxx P P 2222 )sin( 2 1 )cos( 2 1 2 1 2 1 lmlxmyxT PPP 222 2 1 cos 2 1 mlxmlxmTP 2 2 1 xMTC CHƯƠNG 2: MÔ HÌNH HÓA Động năng của hệ thống: Thế năng của hệ thống chính là thế năng vật nặng đầu con lắc: Phương trình Euler – Lagrange: 222 2 1 cos)( 2 1 mlxmlxmMTTT PC cosmglU cos 2 1 cos)( 2 1 222 mglmlxmlxmML 0 LL dt d F x L x L dt d CHƯƠNG 2: MÔ HÌNH HÓA Phương trình Euler – Lagrange: Suy ra: 0sincos )(sin)(cos)( 2 mgmlxm FmlmlxmM 2 2 )(cos sincos)(sin mmM mgmlF x lmMml mlgmMF )()(cos )sin(cos)(sin)(cos 2 2 CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.8: Mô hình hệ tay máy hai bậc tự do l1, l2 : chiều dài của 2 cánh tay m1, m2 : khối lượng φ1, φ2 : góc quay của các khớp cánh tay τ1, τ2 : moment làm quay các khớp nối Tọa độ của cánh tay máy trong hệ tọa độ De-cac: 22112 22112 111 111 coscos sinsin cos sin lly llx ly lx CHƯƠNG 2: MÔ HÌNH HÓA Vận tốc : Động năng: 111 111 1 1 1 sin cos l l y x v 222111 222111 2 2 2 sinsin coscos ll ll y x v )( 2 1 )( 2 1 2 2 2 22 2 1 2 11 yxmyxmT )sinsincos(cos 2 1 2 1 2 1 212121212 2 2 2 22 2 1 2 12 2 1 2 11 llm lmlmlmT CHƯƠNG 2: MÔ HÌNH HÓA Thế năng: )coscos(cos 22112111 llgmglmU )coscos(cos )sinsincos(cos 2 1 2 1 2 1 22112111 212121212 2 2 2 22 2 1 2 12 2 1 2 11 llgmglm llm lmlmlmUTL CHƯƠNG 2: MÔ HÌNH HÓA Phương trình Euler–Lagrange: Thay vào 2 22 1 11 LL dt d LL dt d 11121 2 22121212 221212121 2 121 sin)()sincoscos(sin )sinsincos(cos)( glmmllm llmlmm 2222 2 12121212 121212122 2 22 sin)sincoscos(sin )sinsincos(cos glmllm llmlm CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.9: Mô hình toán bồn chứa chất lỏng (Single Tank) A: tiết diện ngang bồn chứa a: tiết diện van xả k: hệ số tỉ lệ với công suất máy bơm Phương trình cân bằng: Dòng vào: Dòng ra: Trong đó: : áp suất : hệ số xả )()())(( tqtqtAh dt d outin )(.)( tuktqin )()/2()( 222 tpCatq Dout )()( tghtp 6,0 DC CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.9: Mô hình toán bồn chứa chất lỏng (Single Tank) Phương trình cân bằng: ))(2)(.( 1 )( tghaCtuk A th D CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.10: Mô hình toán hệ bồn nối tiếp (Cascade Tank) Phương trình cân bằng: ))(2)(2( 1 )( ))(2)(.( 1 )( 222111 2 2 11111 1 1 tghCatghCa A th tghCatuk A th DD D CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.11: Mô hình toán hệ bồn liên kết (Coupled Tank) Phương trình cân bằng: )||2)sgn(2.( 1 )||2)sgn(2.( 1 2112121222222 2 2 2112211211111 1 1 hhgahhCghCauk A h hhgahhCghCauk A h DD DD CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.12: Sự tương đồng giữa hệ lưu chất và hệ thống điện: Để 2 mô hình trên tương đương ta cần giả thiết bồn chứa rất lớn, khi hệ thống vận hành độ cao mực chất lỏng trong bồn chứa thay đổi không đáng kể. CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.13: Mô hình toán lò sấy θs (t) : nhiệt độ nguồn nhiệt θ (t) : nhiệt độ lò sấy H (t) : dòng nhiệt Dòng nhiệt Phương trình cân bằng: T S R tt tH )()( )( )( )( tH dt td CT CHƯƠNG 2: MÔ HÌNH HÓA Nhiệt trở d: chiều dài lò sấy A: tiết diện ngang k: hệ số dẫn nhiệt CT = cM : nhiệt dung c: nhiệt dung riêng của môi trường truyền nhiệt M: khối lượng môi trường truyền nhiệt Mô hình toán của lò sấy Ak d RT 2 )()( )( tt dt td CR STT CHƯƠNG 2: MÔ HÌNH HÓA Trường hợp lò sấy dài, có thể mô hình hóa bằng cách chia làm nhiều ngăn: Dòng nhiệt: 2 21 2 1 1 1 )()( )( )()( )( T T S R tt tH R tt tH CHƯƠNG 2: MÔ HÌNH HÓA Trường hợp lò sấy dài, có thể mô hình hóa bằng cách chia làm nhiều ngăn: Phương trình cân bằng: Mô hình toán hệ thống )( )( )()( )( 2 2 2 21 1 1 tH dt td C tHtH dt td C T T 2 212 2 2 21 1 11 1 )()()( )()()()()( T T TT S T R tt dt td C R tt R tt dt td C CHƯƠNG 2: MÔ HÌNH HÓA 2.4 PHÂN TÍCH TOÁN HỌC • Kết hợp tất cả các hệ phương trình mô tả đặc tính động của các bộ phận chức năng để được hệ phương trình mô tả hệ thống. • Tuyến tính hóa quan hệ phi tuyến để được mô tả toán học tuyến tính Xét hệ phi tuyến bậc n có p ngõ vào, q ngõ ra mô tả bởi phương trình trạng thái. trong đó: là vector trạng thái, là vector tín hiệu vào, là vector tín hiệu ra; là vector hàm mô tả đặc tính động của hệ phi tuyến. )(),(()( ))(),(()( tutxhty tutxftx ntx )( ptu )( qty )( qn hf (.),(.) CHƯƠNG 2: MÔ HÌNH HÓA Khai triển Taylor xung quanh điểm làm việc tĩnh , ta có thể mô tả hệ thống bằng phương trình trạng thái tuyến tính: Trong đó: )(~)(~)(~ )(~)(~)(~ tutxty tutxtx DC BA xtxtx )()(~ ),( ux ututu )()(~ ytyty )()(~ )),(( uxhy CHƯƠNG 2: MÔ HÌNH HÓA Các ma trận trạng thái của hệ tuyến tính gần đúng được tính như sau: ),(21 2 2 2 1 2 1 2 1 1 1 ),( ... ............ ... ... uxn nnn n n ux x f x f x f x f x f x f x f x f x f x f A CHƯƠNG 2: MÔ HÌNH HÓA Các ma trận trạng thái của hệ tuyến tính gần đúng được tính như sau: ),(21 2 2 2 1 2 1 2 1 1 1 ),( ... ............ ... ... uxn nnn n n ux u f u f u f u f u f u f u f u f u f u f B CHƯƠNG 2: MÔ HÌNH HÓA Các ma trận trạng thái của hệ tuyến tính gần đúng được tính như sau: ),(21 2 2 2 1 2 1 2 1 1 1 ),( ... ............ ... ... uxn qqq n n ux x h x h x h x h x h x h x h x h x h x h C CHƯƠNG 2: MÔ HÌNH HÓA Các ma trận trạng thái của hệ tuyến tính gần đúng được tính như sau: ),(21 2 2 2 1 2 1 2 1 1 1 ),( ... ............ ... ... uxp qqq p p ux u h u h u h u h u h u h u h u h u h u h D CHƯƠNG 2: MÔ HÌNH HÓA Kết hợp các khối trog mô tả toán học hệ thống: • Phương pháp đại số sơ đồ khối – Phương pháp sơ đồ dòng tín hiệu và công thức Mason để tìm hàm truyền tương đương của hệ tuyến tính. • Đánh giá sự phù hợp của mô hình • Dùng mô hình để dự báo đáp ứng của hệ thống đối với tín hiệu vào cho trước. CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.14: Mô hình toán hệ con lắc ngược truyền động dùng động cơ DC, xét ảnh hưởng của ma sát: Đặc tính động của hệ xe–con lắc có xét đến ảnh hưởng của ma sát: Thực hiện Tương tự như thí dụ 2.7, tuy nhiên lực tác động phải kể thêm lực ma sát: Trong đó: fC - lực ma sát tác động lên xe fP - lực ma sát tác động lên con lắc CfFmlmlxmM )(cos)(sin)( 2 Pfmgmlxm sincos CHƯƠNG 2: MÔ HÌNH HÓA * Đặc tính ma sát: Giả thiết có cả ma sát tĩnh và ma sát nhớt tác động làm cản trở chuyển động của xe và con lắc. Các lực ma sát này có thể mô tả bằng các phương trình sau: Trong đó: Ax, Bx, Cx, Aθ, Bθ, Cθ > 0 ||)sgn( || xBeAxf x xC xC x ||)sgn( || BeAf CP CHƯƠNG 2: MÔ HÌNH HÓA * Đặc tính động cơ Trong đó: La : điện cảm phần ứng Ra : điện trở phần ứng Ia : dòng điện phần ứng Va : điện áp phần ứng Eb : sức phản điện (sđđ phần ứng) Kb : Hệ số tốc độ động cơ ω : tốc độ quay động cơ r : bán kính puli Kg : hệ số giảm tốc độ dt dx r K KE EIRV dt dI L g bb baaa a a ; ; CHƯƠNG 2: MÔ HÌNH HÓA * Đặc tính động cơ Trong đó: Jm : moment quán tính động cơ ω : tốc độ quay động cơ Tm : moment động cơ Tl : mô men tải Bm : hệ số ma sát Ki : hệ số mô men Kg : hệ số giảm tốc độ r : bán kính puli Ia : dòng điện phần ứng rFTIKKT BTT dt d J lagim mlm . ; CHƯƠNG 2: MÔ HÌNH HÓA * Hệ phương trình động học của động cơ rFT iKKT BTT dt d J dt dx r K Ke eiRv dt di L l agim mlm g bb baaa a a . FI r KK x r BK x r JK Vx r KK IRIL a gimgmg a gb aaaa 22 CHƯƠNG 2: MÔ HÌNH HÓA * Đặc tính động cơ có thể biểu diễn theo Ia , x và F như sau: FI r KK x r BK x r JK Vx r KK IRIL a gimgmg a gb aaaa 22 CHƯƠNG 2: MÔ HÌNH HÓA Do đó mô hình toán học của hệ xe con lắc với tín hiệu vào là điện áp cấp cho động cơ như sau: FI r KK x r BK x r JK Vx r KK IRIL fmgmlxm fFmlmlxmM a gimgmg a gb aaaa P C 22 2 sincos )(cos)(sin)( CHƯƠNG 2: MÔ HÌNH HÓA Do đó mô hình toán học của hệ xe con lắc với tín hiệu vào là điện áp cấp cho động cơ như sau: a gb aaaa P Ca gimg mg Vx r KK IRIL fmgmlxm fI r KK x r BK mlmlx r JK mM sincos )(cos)(sin)( 2 2 2 CHƯƠNG 2: MÔ HÌNH HÓA Ví dụ 2.15: Xây dựng mô hình tuyến tính của hệ con lắc ngược xung quanh vị trí thẳng đứng. Hệ phương trình mô tả đặc tính động phi tuyến của hệ con lắc ngược (xem ví dụ 2.7) với biến đầu vào là lực tác động vào hệ thống: Véc tơ tín hiệu vào Véc tơ tín hiệu ra: (là tín hiệu có thể ghi nhận được bằng sensor: tốc độ xe và góc nghiêng θ). 2 2 )(cos sincos)(sin mmM mgmlu x lmMml mlgmMu )()(cos )sin(cos)(sin)(cos 2 2 1)( ptu 2)( qty CHƯƠNG 2: MÔ HÌNH HÓA Đặt biến trạng thái: TT xxxxxxtx ],,,[],,,[)( 4321 (.) 2 1 11 2 21 4 2 1 2 21111 2 4 3 2 1 )(cos sincos)(sin )()(cos )sin(cos)(sin)(cos )( f x xmmM xxmgxxmlu x lmMxml xxxmlxgmMxu tx x x x x ))(),(()( tutxftx CHƯƠNG 2: MÔ HÌNH HÓA Biến tín hiệu ra: Điểm cân bằng ở vị trí thẳng đứng: Tuyến tính hóa xung quanh điểm cân bằng: Với các ma trận hệ số A, B, C, D (.) 3 1 )( )( )( h x x tx t ty TT txtyyty )](),([],[)( 21 )0,0(),( ux )(~)(~)(~ )(~)(~)(~ tutxty tutxtx DC BA CHƯƠNG 2: MÔ HÌNH HÓA Xác định các ma trận hệ số A, B, C, D 000 1000 000 0010 )0,0(4 4 3 4 2 4 1 4 4 3 3 3 2 3 1 3 4 2 3 2 2 2 1 2 4 1 3 1 2 1 1 1 )0,0( g M m Ml mM x f x f x f x f x f x f x f x f x f x f x f x f x f x f x f x f x f A CHƯƠNG 2: MÔ HÌNH HÓA Xác định các ma trận hệ số A, B, C, D M Ml u f u f u f u f u f 4 )0,0( 4 3 2 1 )0,0( 1 0 1 0 B CHƯƠNG 2: MÔ HÌNH HÓA Xác định các ma trận hệ số A, B, C, D 0100 0001 )0,0(4 2 3 2 2 2 1 2 4 1 3 1 2 1 1 1 )0,0( x h x h x h x h x h x h x h x h x h C )0,0( )0,0( 2 1 )0,0( 0 0 u h u h u h D
File đính kèm:
 bai_giang_mo_hinh_hoa_nhan_dang_va_mo_phong_chuong_2_mo_hinh.pdf
bai_giang_mo_hinh_hoa_nhan_dang_va_mo_phong_chuong_2_mo_hinh.pdf

