Bài giảng Lý thuyết tín hiệu - Chương 3, Phần 1: Tín hiệu ngẫu nhiên - Võ Thị Thu Sương

TÍN HIỆU NGẪU NHIÊN
 Định nghĩa
 Tín hiệu không đóan được trước khi nó xuất 
hiện
 Không thể mô tả bởi biểu thức tóan học 
 Được mô tả bằng lý thuyết xác xuất 
 Được gọi là “quá trình ngẫu nhiên”
 Quá trình ngẫu nhiên gồm một số hữu hạn các biến 
ngẫu nhiên
 Ví dụ: ( ) 5 c o s ( 2 ) , w h e re i s ra n d o mcx t f t   
1.5 Random Signals
 1.5.1 Biến ngẫu nhiên X(A)
 Biến ngẫu nhiên là một đại lượng thực mà trị của nó phụ 
thuộc vào biến cố ngẫu nhiên. (để biến cố NN có thể được 
mô tả một cách định lượng)
Ví du độ lệch của viên đạn so với mục tiêu là một đại lượng 
phụ thuộc vào kết qủa của lần bắn.
Sự phụ thuộc này được được biểu diễn bởi quy luật xác 
suất gọi chung là phân bố
 Sự phân bố của biến NN được mô tả bởi hàm mật độ xác 
suất PX(x). 
2
1
-
1 2
. n o n -n e g a t iv e : ( ) 0
. n o rm a liz e d : ( ) 1
. e v e n t p ro b a b i li ty : ( )= ( 
2
) 
1
3
X
X
x
X
x
p x
p x d x
P x X x p x d x
 Discrete pdf 
 has the same properties (change integration to summation)
 Two important random variables and their pdf
( )
i
p X x 
0 1
(
. U n i fo rm ra n d o m v a r ia b le
1
 c o n t in u o u s ( ) , f o r 
1
 d i s c re te : ( ) , f o r { , , }
. G a u s s ia n (n o rm a l) r a n d o m 
1
2 v a r ia b le
1
 ( )
2
X
i M
x m
X
X
p x a x b
b a
p X x X x x
M
p x e
 

2
2
)
2
X
X

 Các thông số
 Example:
 Data bits are modeled as uniform random variable with two values
 Symbols are modeled as uniform random variable with M values
 Noise is modeled as Gaussian random variable with zero mean and 
non-zero variance
2 2 2 2
. m e a n : { } ( )
. v a r ia n c e : { ( ) } { }
 (v a r ia n c e = m e a n s q
1
2
u a re v a lu e - m e a n v a lu e s q u a re )
X X
X X X
m E X x p x d x
E X m E X m
1.5 Random Signals
 1.5.2 Random process: X(A,t)
 Là một hàm hai biến A, t time-domain signal waveform with 
some random event
 Usually written as X(t) by embedding A
 Stationary random process
 Average parameters do not depend on time
 We consider stationary random process (signal) only
 Can usually be described conveniently only by average parameters

event time
S ta t io n a ry
. m e a n : ( ) { ( )} c o n s ta n t
. a u to c o rre la t io n ( s ta t io n a ry c a s e ) : 
1
2 ( ) { ( ) ( )}
X X
X
m t E X t m
R E X t X t 
      
 Example (Note: expectation/integration is conducted with 
random variable, not t)
2
0
F in d th e m e a n a n d a u to c o r re la t io n o f th e r a n d o m p ro c e s s
( ) 5 c o s ( 2 ) , w h e re [ 0 , 2 ) i s u n i fo rm ra n d o m .
: 
1
{ ( )} ( ) ( ) 5 c o s ( 2 ) 0
2
( ) { ( ) ( )}
S o lu t
io n
c
X c
X
x t f t
m E x t x t f d f t d
R E x t x t

   
   
 
2
0
= ( ) ( ) ( )
1
 = 5 c o s ( 2 )5 c o s ( 2 2 )
2
2 5
 = c o s ( 2 )
2
c c c
c
x t x t f d
f t f t f d
f

  
    
 
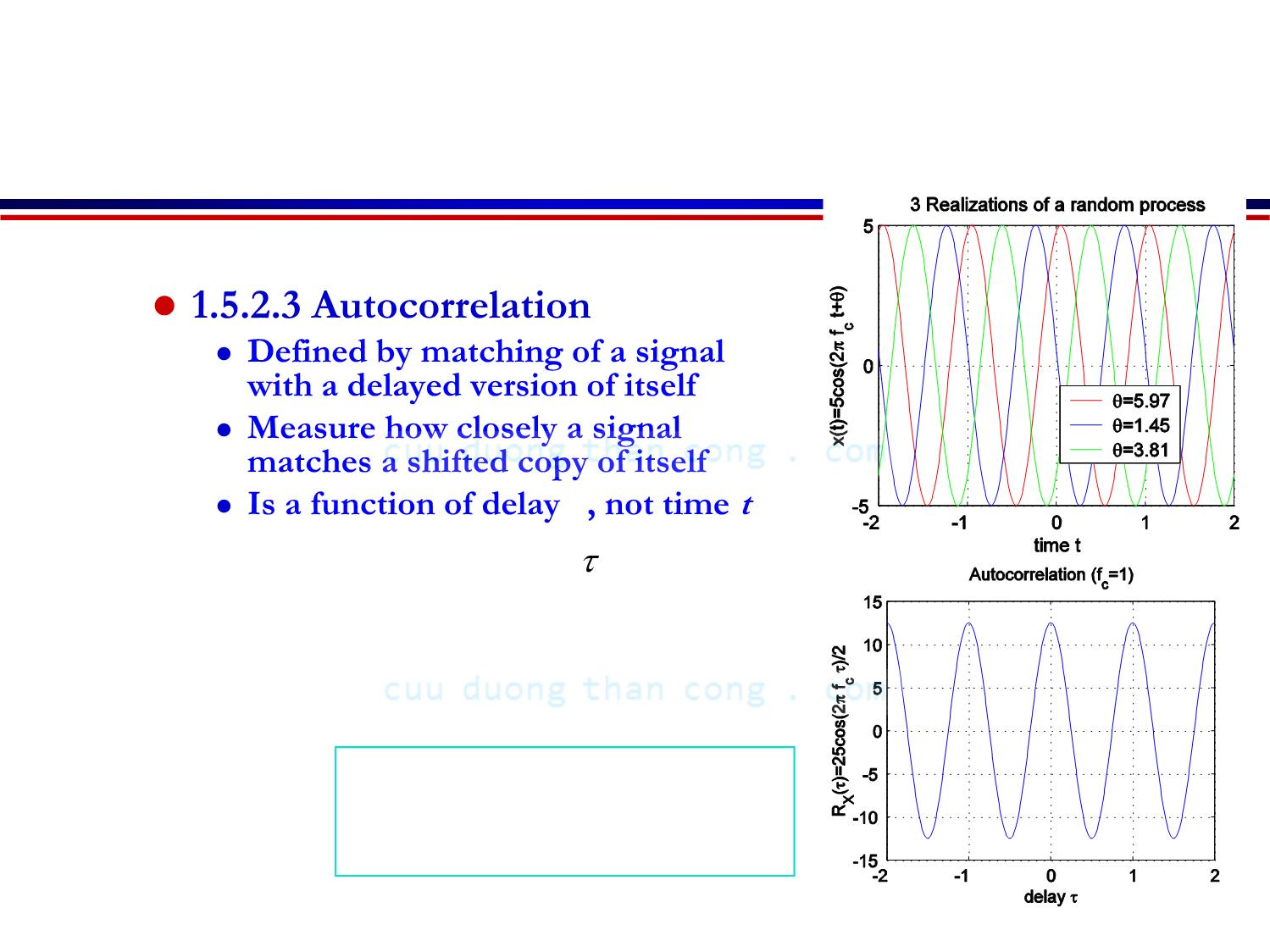
 1.5.2.3 Autocorrelation
 Defined by matching of a signal 
with a delayed version of itself
 Measure how closely a signal 
matches a shifted copy of itself
 Is a function of delay , not time t 

Note for figure: 
Random process cos(2πfct+θ) 
does not look like noise.
 1.5.4 Power Spectral Density (PSD)
 PSD is FT{autocorrelation}
 The only way for frequency-domain 
description of random signal (since 
FT{x(t)} does not exist)
( ) ( )
IF T
x x
F T
G f R     
2 5
E x a m p le : F o r ( ) c o s ( 2 ) , th e P S D is
2
2 5
 ( ) { ( )} [ ( ) ( ) ]
4
x c
x x c c
R f
G f F T R f f f f
 
  
PSD of random 
process 
5cos(2πfct+θ) 
 1.5.3 Parameters and their physical meaning
 Mean & variance of random variable
 Mean, autocorrelation, PSD of random process
-
2
2
2
1 . : d c le v e l o f th e s ig n a l
2 . { ( )} , ( 0 ) , ( ) : a v e ra g e s ig n a l p o w e r
3 . : a v e ra g
4 . F o r s ig n a ls w i th o u t d c z e ro -m e a n
e p o w e r o f A C c o m p o n e n t
 s ig n a ls
i ) 0 . i i ) {
X
X X
X
X X
m
E X t R G
E
f
m
f d


2
( t ) } e q u a ls a v e ra g e s ig n a l p o w e rX
 1.5.5 Noise in communication 
systems
 AWGN: additive white Gaussian 
noise
 Additive: Noise is added (not 
multiplied) to the signal
 White: has constant PSD (equal 
power for all frequency)
 Gaussian: in every time-instant 
(sampling instant), the noise is 
Gaussian random variable
 Noise is usually assumed zero-
mean AWGN
x(t)
n(t)
y(t)
2
2
0
0
2
S ig n a l m o d e l: ( ) ( ) ( )
 P S D : ( ) w a t t s /H z
2
 A u to c o r re la t io n : 
z e ro -m e a n A W G N ( ) p ro p e r t ie s
( ) ( )
2
1
 p d f : ( )
:
 i ) 
i i )
i i i ) 
2
n
n
n
y t x t n t
N
G f
N
R
t
p
n
n e 
  
 
 AWGN is a useful abstract noise model, although it is not 
practical due to infinite power
 In sampled process (discrete process), since δ(0)=1, we 
still have 
 Discrete zero-mean AWGN: power & variance are both N0/2
AWGN PSD & 
Auto-
correlation
2 2 0
{ }
2
N
E X 
1.6 Signal transmission through 
linear systems
 1.6.1 Deterministic signals
x(t) h(t) y(t)
X(f) Y(f)H(f) )()()(
)()()(*)()(
fHfXfY
dthxthtxty

 1.6.2 Random signals
 No Y(f), X(f) exist! But can use PSD.
2
( ) ( ) * ( ) ( ) ( )
( ) ( ) ( )y x
y t h t x t x h t d
G f G f H f
  
 1.6.3 Distortionless transmission & ideal filter
 Distortionless transmission
 Time-domain: only constant magnitude change & a delay
 Frequency domain: constant magnitude response and linear phase 
response
 Ideal filter: distortionless in passband
)(
)()(
fj
efHfH
 
 where
0
p a s s b a n d
( )
0 s to p b a n d
( ) 2
K
H f
f f t 
 Example. Input: AWGN with PSD . System: ideal 
lowpass filter with unit magnitude response in passband fu.. Then 
the output PSD is
0
( ) / 2
n
G f N 
0
2
0
( ) ( ) , ( ) ( )
j f t
y t K x t t Y f K e X f
0
/ 2 , fo r 
( )
0 , O th e rw is e
u u
y
N f f f
G f
Review: Analog 
Communications
 Amplitude modulation
 4 main types, share similar modulator/demodulator
x(t)
tf c 2cos
B.P.F
y(t)
modulator
AM: amplitude modulation
DSB: double-sideband modulation
SSB: single-sideband modulation
VSB: vestigial sideband modulation
y(t)
tf c 2cos
L.P
x(t)
demodulator
 Frequency modulation 
(FM,PM)
 1.7.1 DSB (Page 45-47, 
Page 1022)
 D S B s ig n a l: 
 ( ) ( ) c o s ( 2 )
 D S B s p e c t ru m : 
1
 ( ) [ ( ) ( ) ]
2
 ( ) , ( ) : m e s s a g e s ig n a l a n d s p e c t ru m
 D S B s ig n a l b a n d w i th = 2 * m e s s a g e b a n d w id t h 
c c
c c c
x t x t f t
X f X f f X f f
x t X f
( )
 2
D S B x t
W W 
 DSB demodulation
 DSB is a main digital passband modulation technique
y(t)
tf c 2cos
L.P
x(t)
demodulator
lo w p a s s
lo w p a s s
lo w p a s s
( ) ( ) : r e c e iv e d s ig n a l
D e m o d u la t io n o u tp u t i s :
ˆ ( ) ( ) c o s ( 2 )
 = ( ) c o s ( 2 ) c o s ( 2 )
1
 = ( ) [1 c o s ( 4 ) ]
2
( )
 = 
2
c
c
c c
c
y t x t
x t y t f t
x t f t f t
x t f t
x t
Tín hiệu dừng
(t) là tín hiệu dừng chặt nếu:
    )(),...(),()(),...(),(
2121
 
nn
tttfEtttfE
(t) là tín hiệu dừng rộng nếu:   consttE 
2121
;, ttRttR 
(t) là tín hiệu Egodic nếu: (t) là TH dừng rộng và
T
T
T
dtttR 
*
2
1
lim