Bài giảng Lý thuyết tín hiệu - Chương 1: Một số khái niệm căn bản - Võ Thị Thu Sương

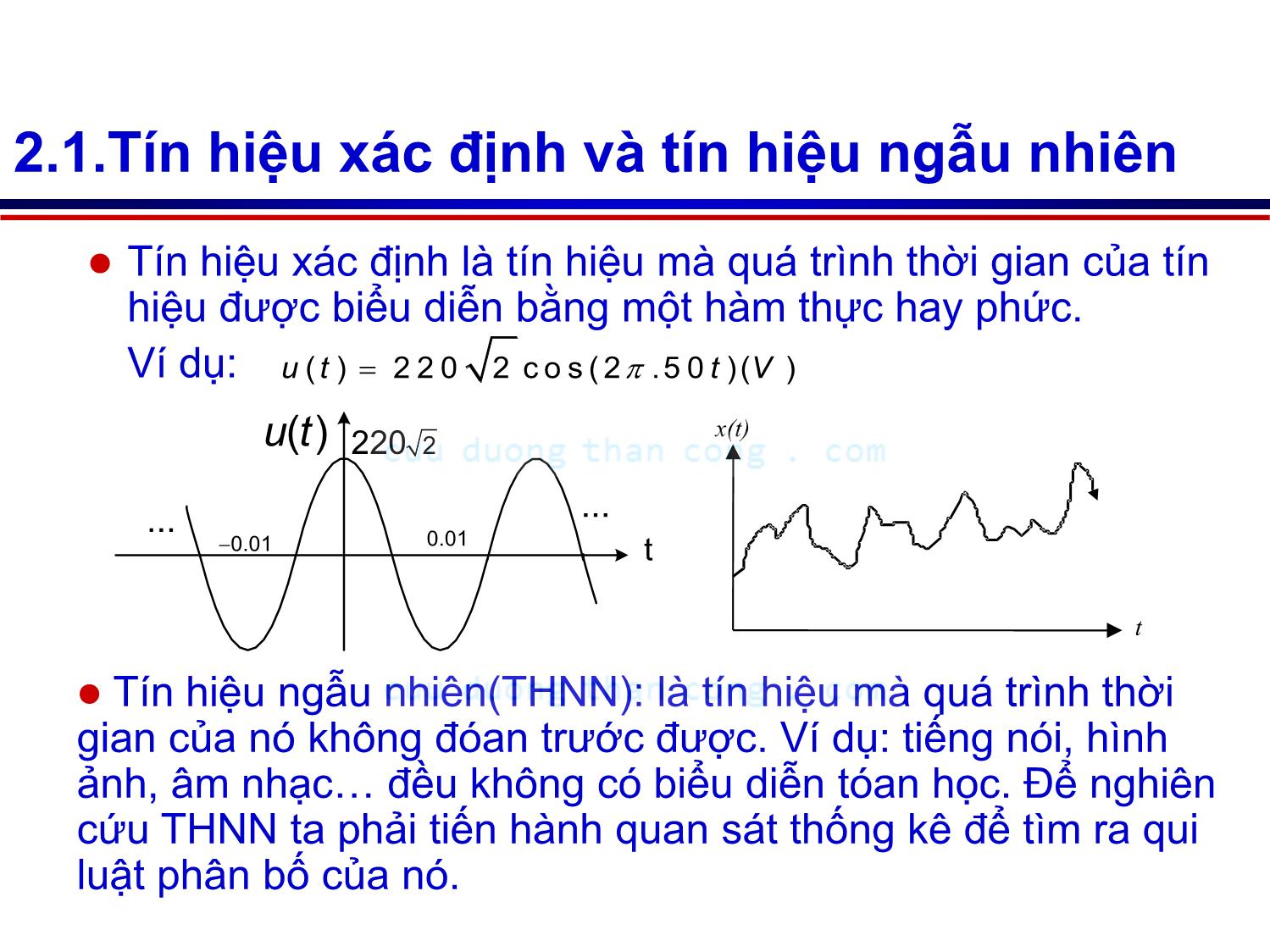
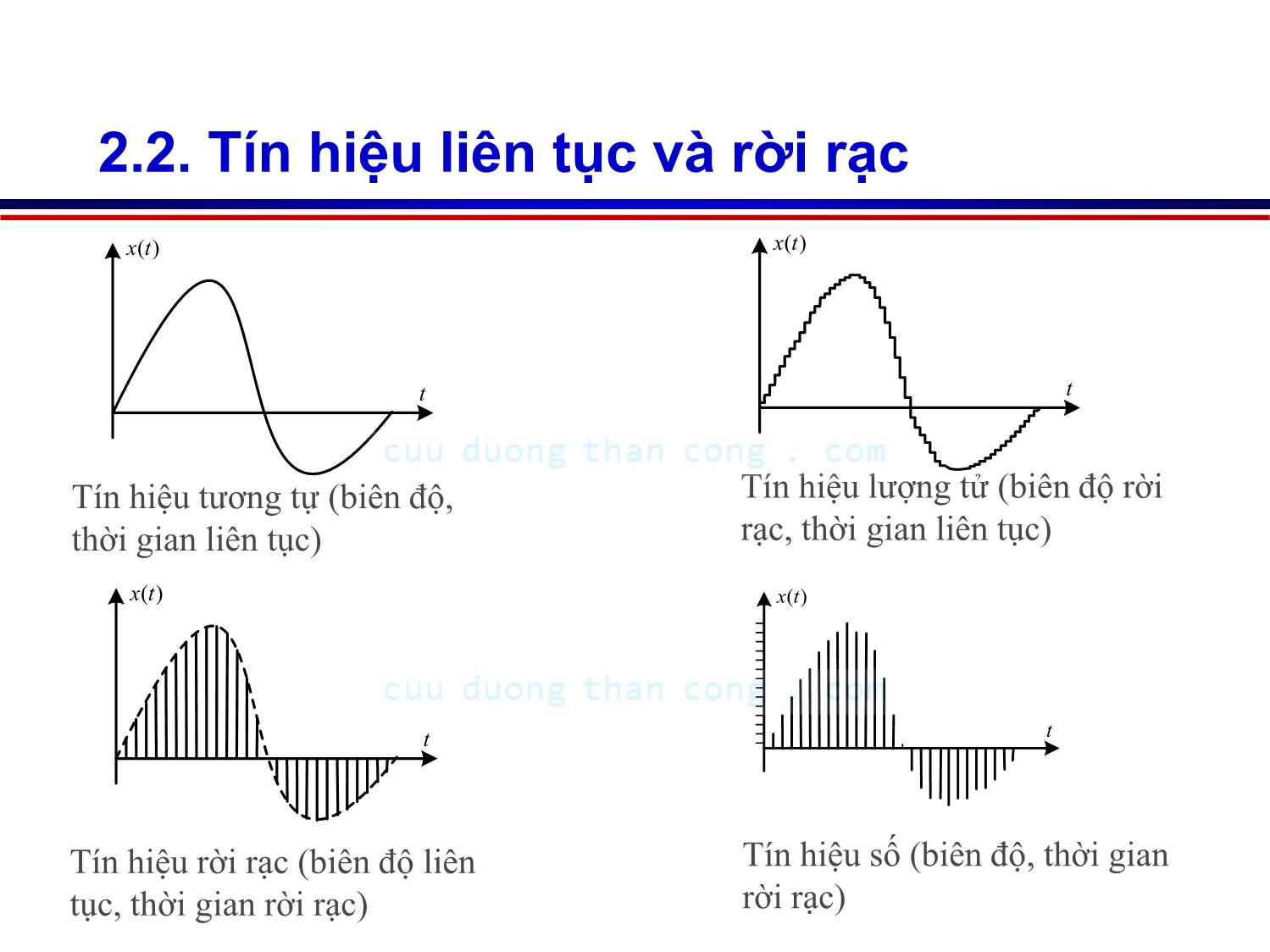
Chương 1: Một số khái niệm căn bản
1. Tín hiệu – Tin tức – Hệ thống
2. Phân lọai tín hiệu
3. Biểu diễn giải tích tín hiệu
1. Tín hiệu- Tin tức- Hệ thống
 Tín hiệu là biểu hiện vật lý của tin tức mà nó mang từ 
nguồn tin đến nơi nhận tin.
Mô hình lý thuyết: hàm theo thời gian x(t)
 Tin tức là những nội dung cần truyền đi qua hình 
ảnh, tiếng nói, số liệu đo lường
 Hệ thống là những thiết bị hay thuật tóan, để thực 
hiện những tác động theo một qui tắc nào đó lên tín 
hiệu để tạo ra một tín hiệu khác
HT
[K]
Tín hiệu 
ngõ vào
Tín hiệu 
ngõ ra
[K] biểu thị cho thuật tóan xử lý
2. Phân loại
2.1. Tín hiệu xác định và tín hiệu ngẫu nhiên
2.2. Tín hiệu liên tục và rời rạc
2.3. Tín hiệu năng lượng – Tín hiệu công suất
2.4. Các phân loại khác
2.1.Tín hiệu xác định và tín hiệu ngẫu nhiên
 Tín hiệu xác định là tín hiệu mà quá trình thời gian của tín 
hiệu được biểu diễn bằng một hàm thực hay phức.
Ví dụ: ( ) 2 2 0 2 c o s ( 2 .5 0 )( )u t t V 
......
0.01
( )u t 2220
t0.01 
x(t)
t
 Tín hiệu ngẫu nhiên(THNN): là tín hiệu mà quá trình thời 
gian của nó không đóan trước được. Ví dụ: tiếng nói, hình 
ảnh, âm nhạc đều không có biểu diễn tóan học. Để nghiên 
cứu THNN ta phải tiến hành quan sát thống kê để tìm ra qui 
luật phân bố của nó.
2.2. Tín hiệu liên tục và rời rạc
)(tx
t
Tín hiệu tương tự (biên độ, 
thời gian liên tục)
)(tx
t
Tín hiệu lượng tử (biên độ rời 
rạc, thời gian liên tục)
)(tx
t
Tín hiệu rời rạc (biên độ liên 
tục, thời gian rời rạc)
)(tx
t
Tín hiệu số (biên độ, thời gian 
rời rạc)
2.3. Tín hiệu năng lượng – TH công suất
 Tín hiệu năng lượng hữu hạn gồm các tín hiệu có thời hạn 
hữu hạn, các tín hiệu quá độ xác định và ngẫu nhiên.
 Tín hiệu công suất trung bình hữu hạn gồm các tín hiệu 
tuần hòan, tín hiệu có thời hạn vô hạn có giá trị tiến đến 
hằng số khác không khi t dần ra vô cùng
2.4. Các phân lọai khác
 Dựa vào bề rộng phổ của tín hiệu có thể phân lọai tín 
hiệu như sau: tín hiệu (TH) tần số thấp, TH tần số cao, 
TH dải rộng, TH dải hẹp.
 Dựa vào biên độ của TH có thể phân lọai thành TH có 
biên độ hữu hạn, TH có biên độ vô hạn.
 Dựa vào biến thời gian của TH có thể phân lọai thành 
TH có thời hạn hữu hạn, TH có thời hạn vô hạn.
 Tín hiệu nhân quả: là tín hiệu có giá trị bằng không khi 
t<0.
3. Biểu diễn giải tích tín hiệu
3.1. Biểu diễn rời rạc
3.1.1 Tín hiệu trực giao
3.1.2 Biểu diễn tín hiệu bằng chuỗi hàm trực 
giao
3.1.3 Một số ví dụ về biểu diễn rời rạc
3.2. Biểu diễn liên tục
3.2.1 Dạng tổng quát
3.2.2 Một số ví dụ về phép biến đổi liên tục
3.1. Biểu diễn rời rạc 
3.1.1 Tín hiệu trực giao
1 2 1 2
. *,x t x t x t x t d t
Tích vô hướng giữa hai tín hiệu được định nghĩa
Nếu tích vô hướng này bằng không thì ta nói hai tín 
hiệu trực giao
Tín hiệu trực chuẩn
)()(
2
)(
1
txtxtx 
1))(),(( txtx
Nếu
và Tín hiệu chuẩn hóa
21
21
21
1
0
),(
xx
xx
xx
3.1.2 Biểu diễn tín hiệu bằng chuỗi hàm trực giao

N
n
nn
ttx
1
)()(  
ni
ni
ni
1
0
,
Tập hàm được chọn, thường là tập hàm trực chuẩn, tức là: )( t
n
 Hệ số khai triển chuỗi được xác định theo phương trình
, 1
( ( ) , ( ) ) ( , )
N
n i n n
i n
x t t   
 
),(
ii
x  Khi đó 
3.1.3 Một số ví dụ về biểu diễn rời rạc
a. Chuỗi Fourier lượng giác
b. Chuỗi Fourier phức
a. Chuỗi Fourier lượng giác
 


 ...2,1);
2
sin(
2
);
2
cos(
2
;
1
)( nt
T
n
T
t
T
n
TT
t
n

Chuỗi Fourier lượng giác được tạo bởi tập hàm trực chuẩn là tập hàm điều hòa sau:
T: chu kỳ tín hiệu

1
0
)
2
sin(
2
)
2
cos(
21
)(
n
nn
t
T
n
T
t
T
n
TT
tx

Tín hiệu x(t) có thể biểu diễn bằng chuỗi Fourier
nn
 ,,
0
T
dttx
TT
xx
0
00
)(
11
,, 
dtt
T
ntx
T
t
T
n
T
x
T
n
)
2
cos()(
2
)
2
cos(
2
,
0
dtt
T
ntx
T
t
T
n
T
x
T
n
)
2
sin()(
2
)
2
sin(
2
,
0
 
Trong đó các hệ số khai triển được xác định như sau:
a. Chuỗi Fourier lượng giác
n
n
n
a
b
arctg 
tdtx
T
a
T
0
0
)(
1
tdtntx
T
a
T
n 
0
0
)(cos)(
2

dttntx
T
b
T
n 
0
0
)(sin)(
2

22
nnn
bac 
T

2
0
a0, an, bn, cn: hệ số khai triển chuỗi 
Fourier.
tần số cơ bản của tín hiệu
T: chu kỳ của tín hiệu
0
)( ) ( c o s s in
0 0
1
x t a a n t b n t
n n
n
  
 
(1)

  
1
0
cos
0
)(
n
ntnncatx  (2)
a. Chuỗi Fourier lượng giác- Ví dụ
2/2/ 
X
t
......
T-T
x(t)
0
2
X
a 
2
, 1, 5 , 9 . . .
2
s in
2 2
, 3 , 7 ,1 1 . . .
n
X
n
X n n
a
n X
n
n
0
n
b 
1
2
0
1
2
( ) 1 c o s
2
n
n
n o d d
X X
x t n t
n

 
1
2
2
1 ,
n
n
X
a n o d d
n 
2T  
a. Chuỗi Fourier lượng giác- Ví dụ
tn
n
tt
ttt
A
0
00
000
cos
1
...9cos
9
1
7cos
7
1
5cos
5
1
3cos
3
1
cos
4



A
T
t
T

2
0
Sóng vuông
n=1
n=3
n=1
n=5
n=41
t
b. Chuỗi Fourier phức
 


 ...2,1,0;
1
)(
2
ne
T
t
t
T
jn
n

Tập hàm điều hòa phức trực chuẩn được chọn:
T: chu kỳ tín hiệu

n
t
T
jn
n
e
T
tx
2
1
)(
2 2
0
1 1
, ( )
T
jn t jn t
T T
n
x e x t e d t
T T
Chuỗi Fourier phức tương ứng

n
tjn
n
eXtx 0)(

T

2
0
Hay:
T
tjn
n
dtetx
T
X
0
0)(
1 
(3)
nn
XC 2 00 X 
2
nn
n
jba
X
Chuỗi (1), (2), (3) có quan hệ với nhau như sau:
a. Chuỗi Fourier phức - Ví dụ
2/2/ 
X
t
......
T-T
x(t)
0
2
2
1
s in
2
jn t
n
X n
X X e d t
T n



0
( ) s in c o s
2n
X n
x t n t
n

 
3.2. Biểu diễn liên tục TH 
3.2.1 Dạng tổng quát

 dtsttxsX ),()()(

 dstssXtx ),()()( 
)()( sXtx 
),( st 
),( ts
Biến đổi thuận
Biến đổi ngược
được gọi là nhân biến đổi
được gọi là nhân liên hợp
3.2.2 Một số ví dụ về phép biến đổi liên tục
Biến đổi Fourier  


 ( ) ( ) ( )
j t
X F x t x t e d t
( ) ( )x t X 

  
1 1
( ) ( )
2
j t
x t F X X e d
Biến đổi Laplace
 
0
( ) ( ) ( )
s t
X s L x t x t e d t
  
1
1
( ) t 0
2( ) ( )
0 t< 0
c j
s t
c j
X s e d s
jx t L X s
)()( sXtx 
 js 
Biến đổi Hilbert )(ˆ)( txtx 
  


d
t
x
txHtx 
)(1
)()(ˆ   


d
t
x
txHtx 
)(ˆ1
)(ˆ)(
1
• Biến đổi Fourier-Ví dụ
A 
f
fA
fX
 
s in
 
f 
X ( f ) 
1 
τ 
2 
τ 
3 
τ 
4 
τ 
6 
τ 
5 
τ 
7 
τ 
-1 
τ 
-2 
τ 
-3 
τ 
-4 
τ 
-6 
τ 
- 5 
τ 
-7 
τ 
t
A
τ
2
τ
x(t)
τ
2
Bài tập
1. Tìm chuỗi Fourier lượng giác và chuỗi Fourier phức các tín hiệu sau
X(t)
-1 3 4-4
......
-3
1
t
......
2
4sin2( ) tx t 
2
......
2 
( )x t
 2 
......
4
( )x t
4
Bài tập
2. Tìm X() của các tín hiệu sau:
2
. ( )
t
a x t e
1 1 0
. ( ) 1 0 1
0 1
t t
b x t t t
t
1 1 0
. ( ) 1 0 1
0 1
t
c x t t
t
3. Tìm x(t) biết các X() như sau:
. ( )a X e


2
. ( ) 2
0 2
b X


