Bài giảng Lý thuyết mật mã - Chương 5: Mật mã khóa công khai - Đỗ Trọng Tuấn
Giới thiệu sơ lược hệ mật mã khóa
công khai
Symmetric and asymmetric-key cryptography will exist
in parallel and continue to serve the community. We
actually believe that they are complements of each
other; the advantages of one can compensate for the
disadvantages of the other.
Giới thiệu sơ lược hệ mật mã khóa
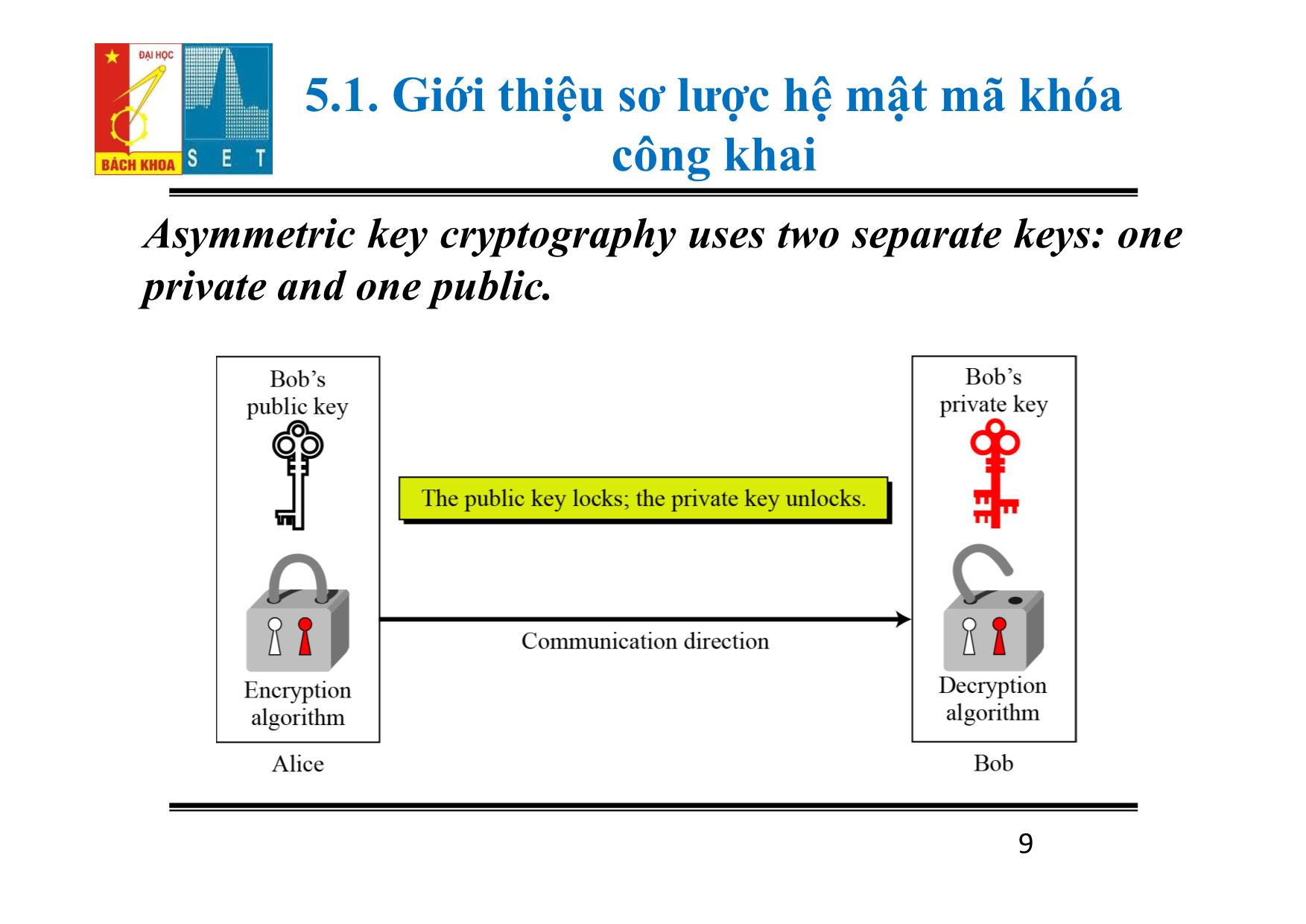
công khai
Symmetric and asymmetric-key cryptography will exist in parallel
and continue to serve the community. We actually believe that
they are complements of each other; the advantages of one can
compensate for the disadvantages of the other.
Symmetric-key cryptography is based on sharing secrecy;
asymmetric-key cryptography is based on personal secrecy.
There is a very important fact that is sometimes misunderstood:
The advent of asymmetric-key cryptography does not eliminate
the need for symmetric-key cryptography.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8
Trang 9
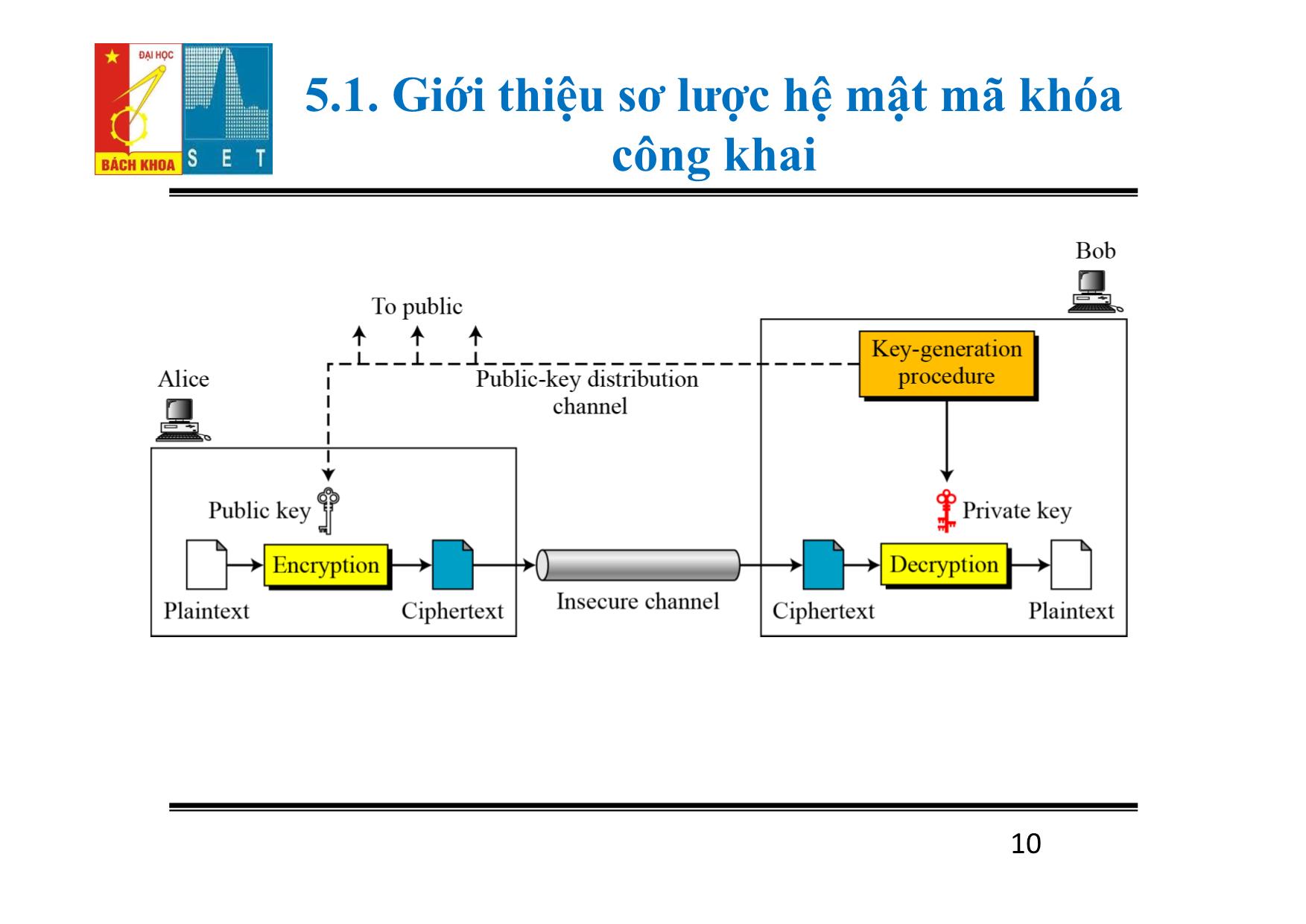
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Lý thuyết mật mã - Chương 5: Mật mã khóa công khai - Đỗ Trọng Tuấn

TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI VIỆN ĐIỆN TỬ - VIỄN THÔNG BỘ MÔN ĐIỆN TỬ HÀNG KHÔNG VŨ TRỤ Môn học: LÝ THUYẾT MẬT MÃ Giảng viên: PGS.TS. Đỗ Trọng Tuấn Email: dotrongtuan@gmail.com 6/10/2016 1 Mục tiêu học phần Cung cấp kiến thức cơ bản về mật mã đảm bảo an toàn và bảo mật thông tin: Các phương pháp mật mã khóa đối xứng; Phương pháp mật mã khóa công khai; Các hệ mật dòng và vấn đề tạo dãy giả ngẫu nhiên; Lược đồ chữ ký số Elgamal và chuẩn chữ ký số ECDSA; Độ phức tạp xử lý và độ phức tạp dữ liệu của một tấn công cụ thể vào hệ thống mật mã; Đặc trưng an toàn của phương thức mã hóa; Thám mã tuyến tính, thám mã vi sai và các vấn đề về xây dựng hệ mã bảo mật cho các ứng dụng. 2 Nội Dung 1. Chương 1. Tổng quan 2. Chương 2. Mật mã khóa đối xứng 3. Chương 3. Hệ mật DES 4. Chương 4. Hệ mật AES 5. Chương 5. Mật mã khóa công khai 6. Chương 6. Kỹ thuật quản lý khóa 6/10/2016 3 Tài liệu tham khảo 1. A. J. Menezes, P. C. Van Oorschot, S. A. Vanstone, Handbook of applied cryptography, CRC Press 1998. 2. B. Schneier, Applied Cryptography. John Wiley Press 1996. 3. M. R. A. Huth, Secure Communicating Systems, Cambridge University Press 2001. 4. W. Stallings, Network Security Essentials, Applications and Standards, Prentice Hall. 2000. 4 Nhiệm vụ của Sinh viên 1. Chấp hành nội quy lớp học 2. Thực hiện đầy đủ bài tập 3. Nắm vững ngôn ngữ lập trình Matlab 5 Chương 5. Mật mã khóa công khai 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai 5.2. Hệ mật RSA 5.3. Hệ mật RABIN 5.4. Hệ mật Elgamal 6 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai Symmetric and asymmetric-key cryptography will exist in parallel and continue to serve the community. We actually believe that they are complements of each other; the advantages of one can compensate for the disadvantages of the other. 7 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai Symmetric and asymmetric-key cryptography will exist in parallel and continue to serve the community. We actually believe that they are complements of each other; the advantages of one can compensate for the disadvantages of the other. Symmetric-key cryptography is based on sharing secrecy; asymmetric-key cryptography is based on personal secrecy. There is a very important fact that is sometimes misunderstood: The advent of asymmetric-key cryptography does not eliminate the need for symmetric-key cryptography. 8 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai Asymmetric key cryptography uses two separate keys: one private and one public. 9 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai 10 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai Plaintext/Ciphertext Unlike in symmetric-key cryptography, plaintext and ciphertext are treated as integers in asymmetric-key cryptography. Encryption/Decryption C = f (Kpublic , P) P = g(Kprivate , C) 11 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai The main idea behind asymmetric-key cryptography is the concept of the trapdoor one-way function. A function as rule mapping a domain to a range 12 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai One-Way Function (OWF) 1. f is easy to compute. 2. f −1 is difficult to compute. Trapdoor One-Way Function (TOWF) 3. Given y and a trapdoor, x can be computed easily. 13 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai Ví dụ When n is large, n = p × q is a one-way function. Given p and q , it is always easy to calculate n ; given n, it is very difficult to compute p and q. This is the factorization problem. Ví dụ When n is large, the function y = xk mod n is a trapdoor one- way function. Given x, k, and n, it is easy to calculate y. Given y, k, and n, it is very difficult to calculate x. This is the discrete logarithm problem. However, if we know the trapdoor, k′ such that k × k ′ = 1 mod f(n), we can use x = yk′ mod n to find x. 14 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai Knapsack Cryptosystem Definition a = [a1, a2, , ak ] and x = [x1, x2, , xk]. Given a and x, it is easy to calculate s. However, given s and a it is difficult to find x. Superincreasing Tuple ai ≥ a1 + a2 + + ai−1 15 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai 16 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai Ví dụ As a very trivial example, assume that a = [17, 25, 46, 94, 201,400] and s = 272 are given. Table 10.1 shows how the tuple x is found using inv_knapsackSum routine in Algorithm 10.1. In this case x = [0, 1, 1, 0, 1, 0], which means that 25, 46, and 201 are in the knapsack. 17 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai Secret Communication with Knapsacks. 18 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai 19 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai 20 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai 21 5.1. Giới thiệu sơ lược hệ mật mã khóa công khai This is a trivial (very insecure) example just to show the procedure. 22 5.2. Hệ mật RSA The most common public-key algorithm is the RSA cryptosystem, named for its inventors (Rivest, Shamir, and Adleman). 23 5.2. Hệ mật RSA 24 5.2. Hệ mật RSA 25 5.2. Hệ mật RSA Encryption, decryption, and key generation in RSA 26 5.2. Hệ mật RSA Two Algebraic Structures Encryption/Decryption Ring: R = Key-Generation Group: G = 27 5.2. Hệ mật RSA 28 5.2. Hệ mật RSA Euler’s phi-function, f (n), which is sometimes called the Euler’s totient function plays a very important role in cryptography. 29 5.2. Hệ mật RSA 30 5.2. Hệ mật RSA Encryption 31 5.2. Hệ mật RSA Decryption 32 5.3. Hệ mật RABIN The Rabin cryptosystem can be thought of as an RSA cryptosystem in which the value of e and d are fixed. The encryption is C ≡ P2 (mod n) and the decryption is P ≡ C1/2 (mod n). 33 5.3. Hệ mật RABIN Rabin cryptosystem 34 5.3. Hệ mật RABIN Key Generation 35 5.3. Hệ mật RABIN Encryption 36 5.3. Hệ mật RABIN Decryption The Rabin cryptosystem is not deterministic: Decryption creates four plaintexts. 37 5.4. Hệ mật ELGAMAL Key generation, encryption, and decryption in ElGamal 38 5.4. Hệ mật ELGAMAL Key Generation 39 5.4. Hệ mật ELGAMAL 40 5.4. Hệ mật ELGAMAL 41 5.4. Hệ mật ELGAMAL The bit-operation complexity of encryption or decryption in ElGamal cryptosystem is polynomial. 42
File đính kèm:
 bai_giang_ly_thuyet_mat_ma_chuong_5_mat_ma_khoa_cong_khai_do.pdf
bai_giang_ly_thuyet_mat_ma_chuong_5_mat_ma_khoa_cong_khai_do.pdf

