Bài giảng Lý thuyết mật mã - Chương 2: Mật mã khóa đối xứng - Đỗ Trọng Tuấn
Giới thiệu sơ lược hệ mật mã khóa
đối xứng cổ điển
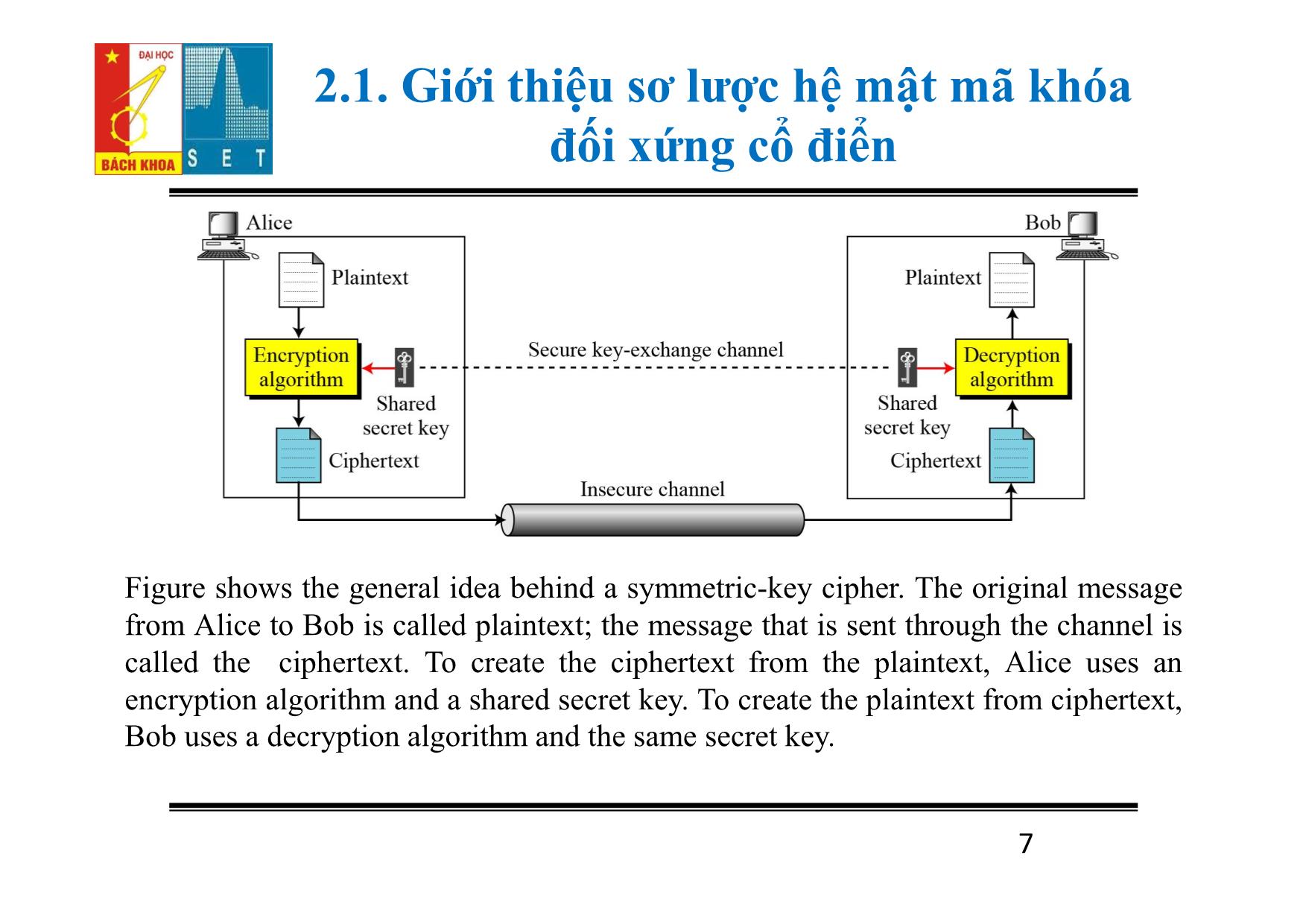
Figure shows the general idea behind a symmetric-key cipher. The original message
from Alice to Bob is called plaintext; the message that is sent through the channel is
called the ciphertext. To create the ciphertext from the plaintext, Alice uses an
encryption algorithm and a shared secret key. To create the plaintext from ciphertext,
Bob uses a decryption algorithm and the same secret key.
Based on Kirchhoff's principle, one should always assume
that the adversary, Eve, knows the encryption/decryption
algorithm. The resistance of the cipher to attack must be based
only on the secrecy of the key
Hệ mật mã khóa đối xứng thay thế
• Đây là hệ mật mã thay thế một ký tự này thành một
ký tự khác.
• Phân loại:
– Mật mã thay thế đơn ký tự - monoalphabetic
– Mật mã thay thế đa ký tự - polyalphabetic

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Lý thuyết mật mã - Chương 2: Mật mã khóa đối xứng - Đỗ Trọng Tuấn

i xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Vigenere Cipher
We can encrypt the message “She is listening” using the 6-
character keyword “PASCAL”.
31
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Vigenere Cipher
We can encrypt the message “She is listening” using the 6-
character keyword “PASCAL”.
The initial key stream is (15, 0,
18, 2, 0, 11)
32
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Hãy so sánh Vigenere cipher với Additive Cipher?
A Vigenere cipher as a combination of m additive ciphers
33
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Hãy so sánh Vigenere cipher với Additive Cipher?
Ngược lại: the additive
cipher is a special case
of Vigenere cipher in
which m = 1.
34
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Thám mã Vigenere Cipher
Giả sử hacker nhận được bản tin mật sau:
Làm thế nào để
giải mã????
Theo phương pháp Kasiski, từng cụm 3 chữ liên tiếp được khảo sát
trong cả đoạn để tìm khoảng cách ngắn nhất mà cụm đó xuất hiện lặp
lại
35
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Thám mã Vigenere Cipher
Giả sử hacker nhận được bản tin mật sau:
Theo phương pháp Kasiski, từng cụm 3 chữ liên tiếp được khảo sát
trong cả đoạn để tìm khoảng cách ngắn nhất mà cụm đó xuất hiện lặp
lại
36
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Thám mã Vigenere Cipher
The greatest common divisor of differences is 4, which means that the
key length is multiple of 4. First try m = 4.
37
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Hill Cipher
Key in the Hill cipher
The key matrix in the Hill cipher needs to
have a multiplicative inverse.
38
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Hill Cipher
Ví dụ 9: Hãy mã hóa bản tin “code is ready” bằng hệ mật Hill với
khóa K
39
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Hill Cipher
40
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Thám mã hệ mật Hill
• Việc thám mã hệ mật Hill bằng cách dò lần lượt các từ khóa là dường như
không thực hiện được.
• Hệ mật này gần như chỉ có thể bị phá được khi biết được giá trị � và các cặp
chữ tương ứng giữa bản mật và bản rõ.
• Ví dụ: với � = 3
41
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật thay thế đa ký tự - Polyalphabetic
Thám mã hệ mật Hill
• Do P là ma trận khả nghịch, nên người thám mã sẽ tìm ma trận P-1, rồi tìm khóa
K
Từ đó, người thám mã sẽ phá được tất cả các bản mật sử dụng khóa K nói
trên
42
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
2.2.2. Hệ mật mã khóa đối xứng dịch chuyển vị trí –
Transposition Ciphers
A transposition cipher does not substitute one symbol for
another, instead it changes the location of the symbols.
A transposition cipher reorders symbols.
a. Hệ mật dịch chuyển không khóa - Keyless Transposition Ciphers
b. Hệ mật dịch chuyển có khóa - Keyed Transposition Ciphers
c. Hệ mật dịch chuyển kết hợp - Combination of Two Approaches
43
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
a. Hệ mật dịch chuyển không khóa
• Đây là hệ mật mã cổ điển đơn giản, được sử dụng từ lâu.
• Hệ mật mã dựa trên sự hoán vị của các ký tự trong bản rõ
để có được bản mật.
• Có 2 phương pháp:
– Chia cột – ghép hàng
– Chia hàng – ghép cột
44
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
a. Hệ mật dịch chuyển không khóa
• A good example of a keyless cipher using the first method is
the rail fence cipher.
• The plaintext is arranged in 2 lines as a zigzag pattern.
• The ciphertext is created by reading the pattern row by row.
45
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
a. Hệ mật dịch chuyển không khóa
• Alice and Bob can agree on the number of columns and use
the second method.
• Alice writes the same plaintext, row by row, in a table of four
columns.
46
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật dịch chuyển có khóa
• The keyless ciphers permute the characters by using writing
plaintext in one way and reading it in another way.
• The permutation is done on the whole plaintext to create the
whole ciphertext.
• Another method is to divide the plaintext into groups of
predetermined size, called blocks, and then use a key to
permute the characters in each block separately. => Keyed
transposition ciphers
47
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
b. Hệ mật dịch chuyển có khóa
Alice needs to send the message “Enemy attacks tonight” to
Bob.
The key used for encryption and decryption is a permutation
key.
Key
48
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
c. Hệ mật dịch chuyển kết hợp
49
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
c. Hệ mật dịch chuyển kết hợp
50
2.2. Một số hệ mật mã khóa đối xứng
cổ điển
Biểu diễn hệ mật dịch chuyển bằng ma trận
51
2.3. Sơ lược hệ mật mã dòng
và mã khối
• Các hệ mật mã khóa đối xứng có thể được phân loại thành 2
loại hệ mật: Hệ mật mã dòng và hệ mật mã khối
52
2.3. Sơ lược hệ mật mã dòng và mã
khối
2.3.1. Hệ mật mã dòng
Với bản rõ dòng P, bản mật dòng C và khóa dòng K, ta có:
Ví dụ
53
2.3. Sơ lược hệ mật mã dòng và mã
khối
2.3.1. Hệ mật mã dòng
Hệ mật mã cộng có phải là hệ mật dòng hay không?
Hệ mật mã thay thế đơn ký tự có phải là hệ mật dòng hay
không?
54
2.3. Sơ lược hệ mật mã dòng và mã
khối
2.3.2. Hệ mật mã khối
A group of plaintext symbols of size m (m > 1) are encrypted
together creating a group of ciphertext of the same size
55
2.3. Sơ lược hệ mật mã dòng và mã
khối
2.3.2. Hệ mật mã khối
• Hill ciphers are block ciphers.
• A block of plaintext, of size 2 or more is encrypted together
using a single key (a matrix).
• In these ciphers, the value of each character in the ciphertext
depends on all the values of the characters in the plaintext.
• The key is made of m × m values, it is considered as a single
key.
56
2.3. Sơ lược hệ mật mã dòng và mã
khối
2.3.1. Hệ mật mã khối
• In practice, blocks of plaintext are encrypted individually, but
they use a stream of keys to encrypt the whole message block
by block.
• In other words, the cipher is a block cipher when looking at
the individual blocks, but it is a stream cipher when looking at
the whole message considering each block as a single unit.
57
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
Nhóm Vành Trường
58
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
• A group (G) is a set of elements with a binary operation (•)
that satisfies four properties:
– Closure
– Associativity
– Existence of identity
– Existence of inverse
59
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
• A commutative group satisfies an extra property,
commutatively or abelian group
– Closure
– Commutativity
– Associativity
– Existence of identity
– Existence of inverse
60
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
• A commutative group satisfies an extra property,
commutatively or abelian group
– Closure: �, � ∈ � �ℎì � = a (•) b ∈ �
– Commutatively: � � � = � � �
– Associativity: c(•)(� � �) = c(•)� � �
– Existence of identity: � � � = � � � = �
– Existence of inverse: � � �� = �� � � = �
61
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
• A very interesting group is the permutation group. The set is the set of all
permutations, and the operation is composition: applying one permutation
after another.
62
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
• A very interesting group is the permutation group. The set is the set of all
permutations, and the operation is composition: applying one permutation
after another.
63
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
• Finite Group
Nhóm hữu hạn là nhóm có số hữu hạn các phần tử
• Order of a Group
Cấp của nhóm là số phần tử của nhóm đó
• Subgroup
Nhóm con của một nhóm G là nhóm bao gồm các phần tử
thuộc G đồng thời thỏa mãn phép toán đóng trong G
64
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
• Tính chất của subgroup
65
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
Cyclic Subgroups
• Nhóm con Cyclic là nhóm được tạo ra bởi cấp số của 1
phần tử nhóm gốc
• Cấp số của phần tử là số lần thực hiện lặp lại phép toán đối
với phần tử đó
66
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
Cyclic Group
• Nhóm G là nhóm Cyclic khi G chính là nhóm con Cyclic
67
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.1. Nhóm
Lagrange’s Theorem
Assume that G is a group, and H is a subgroup of G. If the order
of G and H are |G| and |H|, respectively, then, based on this
theorem, |H| divides |G|.
Order of an Element
The order of an element, ord(a), is the smallest integer that
�� = �.
68
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.2. Vành
A ring, R = , is an algebraic structure with two operations.
The second operation must be distributed over the first
�∎ � ∘ � = (�∎�) ∘ (�∎�)
(� ∘ �)∎� = (�∎�) ∘ (�∎�)
69
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.2. Vành
The second operation must be distributed over the first
�∎ � ∘ � = (�∎�) ∘ (�∎�)
(� ∘ �)∎� = (�∎�) ∘ (�∎�)
The set Z with two operations, addition and multiplication, is a
commutative ring. We show it by R = . Addition
satisfies all of the five properties; multiplication satisfies only
three properties.
70
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường
A field, denoted by F = is a commutative ring in
which the second operation satisfies all five properties defined
for the first operation except that the identity of the first
operation has no inverse.
71
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường
• A finite field, a field with a finite number of elements, are
very important structures in cryptography.
• Galois showed that for a field to be finite, the number of
elements should be ��, where p is a prime and n is a
positive integer.
A Galois field, GF(pn), is a finite field
with pn elements.
72
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường
A Galois field, GF(pn), is a finite field
with pn elements.
When n = 1, we have GF(p) field. This field can be the set Zp,
{0, 1, , p − 1}, with two arithmetic operations.
A very common field in this category is GF(2) with the set {0,
1} and two operations, addition and multiplication.
a 0 1 a 0 1
-a 0 1 a-1 N/A 1
73
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n)
In cryptography, we often need to use four operations
(addition, subtraction, multiplication, and division). In
other words, we need to use fields. We can work in
GF(2n) and uses a set of 2n elements. The elements in
this set are n-bit words.
4.2.1 Polynomials
4.2.2 Using A Generator
4.2.3 Summary
74
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n)
Let us define a GF(22) field in which the set has four 2-bit words:
{00, 01, 10, 11}. We can redefine addition and multiplication for
this field in such a way that all properties of these operations are
satisfied.
An example of GF(22) field 75
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Polynomials
A polynomial of degree n − 1 is an expression
of the form
i th
where x is called the i term and ai is called coefficient
of the ith term.
76
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Polynomials
How we can represent the 8-bit word (10011001)
using a polynomials?
77
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Polynomials
To find the 8-bit word related to the polynomial x5 + x2 + x, we
first supply the omitted terms. Since n = 8, it means the
polynomial is of degree 7.
The expanded polynomial is
This is related to the 8-bit word 00100110.
78
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Polynomials
Lưu ý:
Polynomials representing n-bit words
use two fields: GF(2) and GF(2n)
79
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Modulus
For the sets of polynomials in GF(2n), a group of
polynomials of degree n is defined as the modulus. Such
polynomials are referred to as irreducible polynomials.
80
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Modulus
Lưu ý:
Addition and subtraction operations on
polynomials are the same operation.
81
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Modulus
Let us do (x5 + x2 + x) (x3 + x2 + 1) in GF(28). We use the symbol
to show that we mean polynomial addition.
The following shows the procedure:
82
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Modulus
There is also another short cut. Because the addition in GF(2)
means the exclusive-or (XOR) operation. So we can exclusive-or
the two words, bits by bits, to get the result. In the previous
example, x5 + x2 + x is 00100110 and x3 + x2 + 1 is 00001101. The
result is 00101011 or in polynomial notation x5 + x3 + x + 1.
83
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Multiplication
1. The coefficient multiplication is done in GF(2).
2. The multiplying xi by xj results in xi+j
3. The multiplication may create terms with degree more
than n − 1, which means the result needs to be reduced
using a modulus polynomial.
84
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Generator
Sometimes it is easier to define the elements of the
GF(2n) field using a generator.
85
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Generator
Generate the elements of the field GF(24) using the irreducible
polynomial ƒ(x) = x4 + x + 1.
86
2.4. Cơ sở toán học cho hệ mật mã
khóa đối xứng hiện đại
2.4.3. Trường GF(2n) Summary
The finite field GF(2n) can be used to define four
operations of addition, subtraction, multiplication and
division over n-bit words. The only restriction is that
division by zero is not defined.
87File đính kèm:
 bai_giang_ly_thuyet_mat_ma_chuong_2_mat_ma_khoa_doi_xung_do.pdf
bai_giang_ly_thuyet_mat_ma_chuong_2_mat_ma_khoa_doi_xung_do.pdf

