Bài giảng Lý thuyết mạch - Chương 3: Mạch khuếch đại và khuếch đại thuật toán - Phạm Khánh Tùng
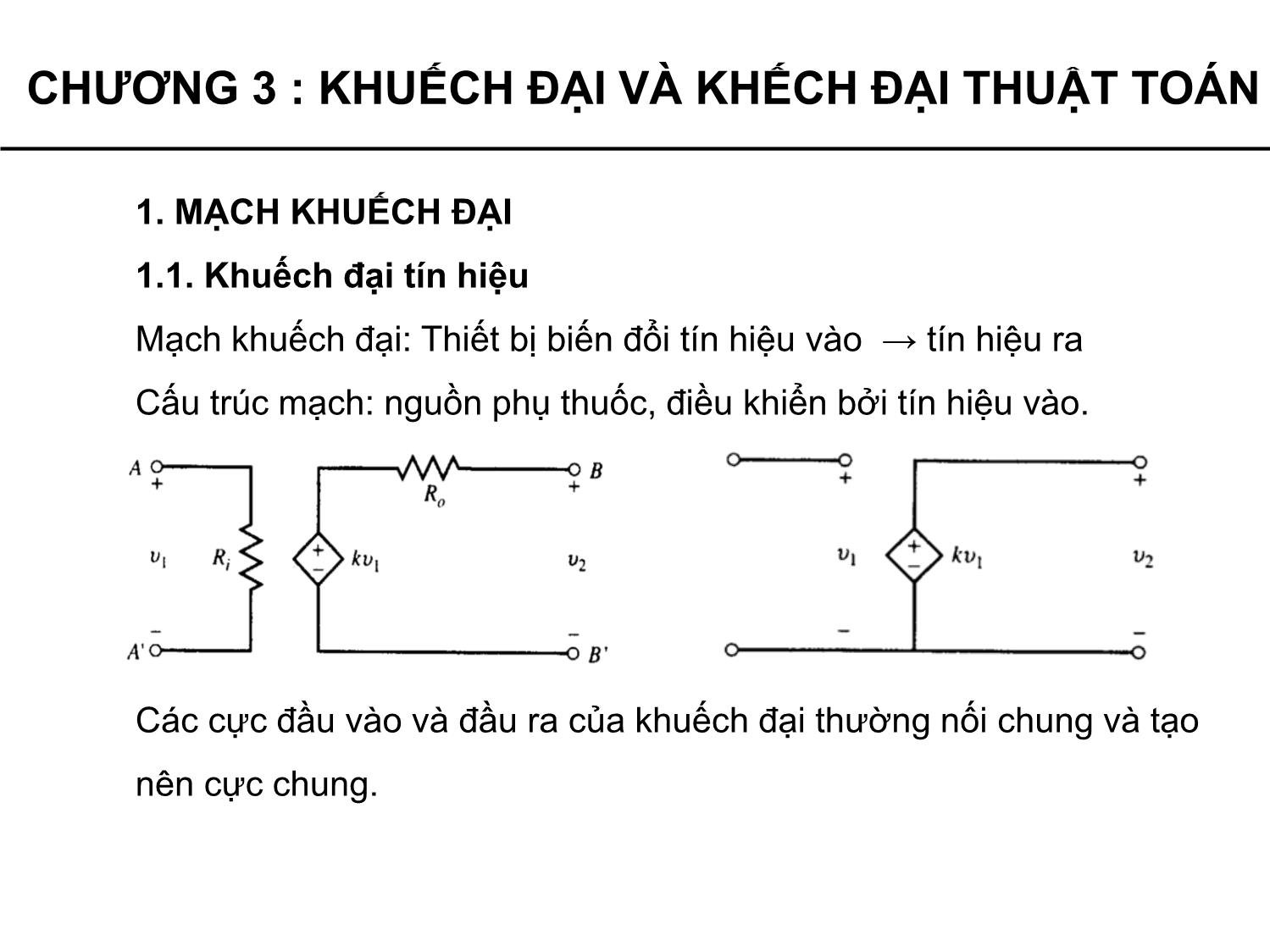
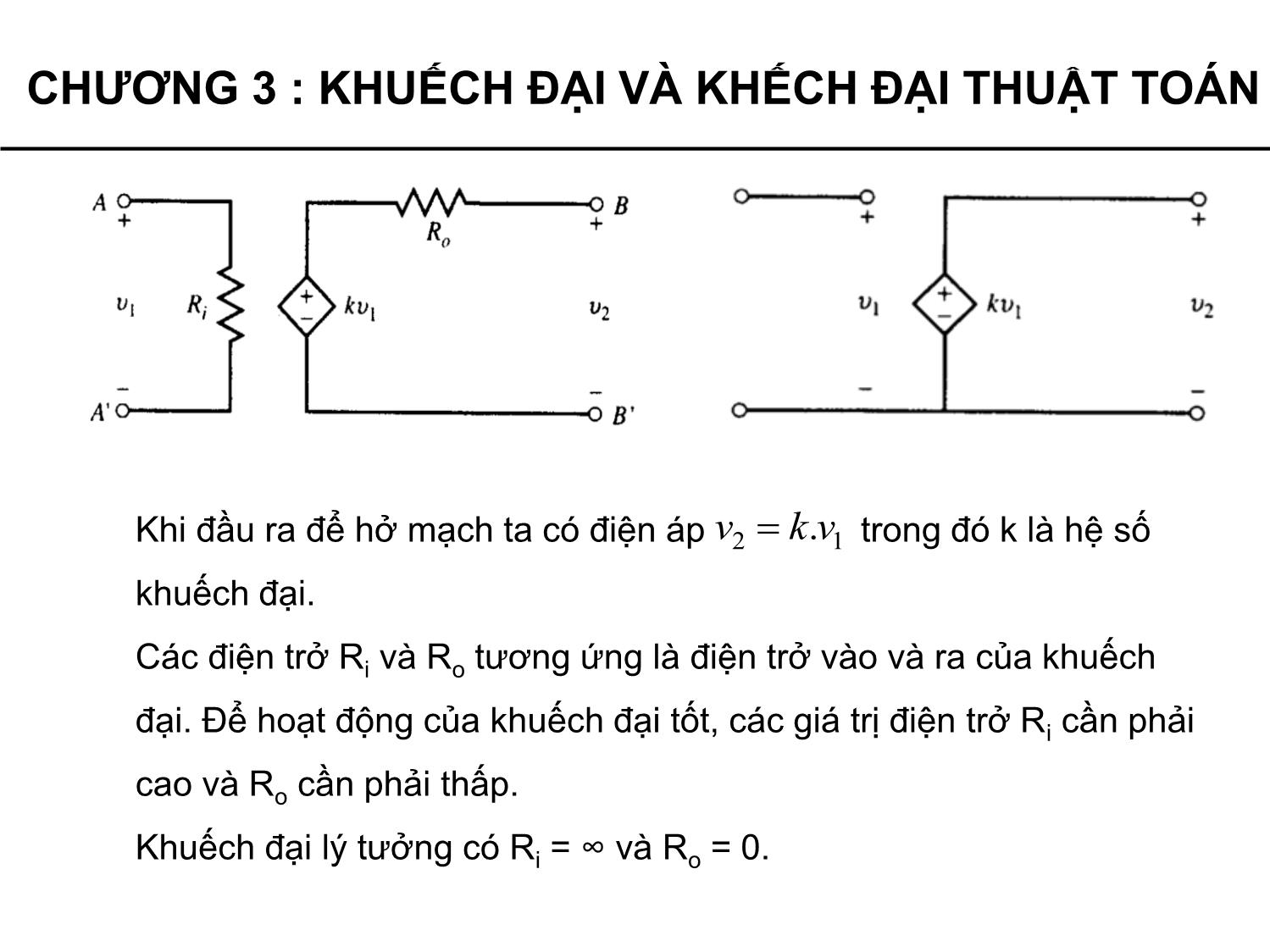
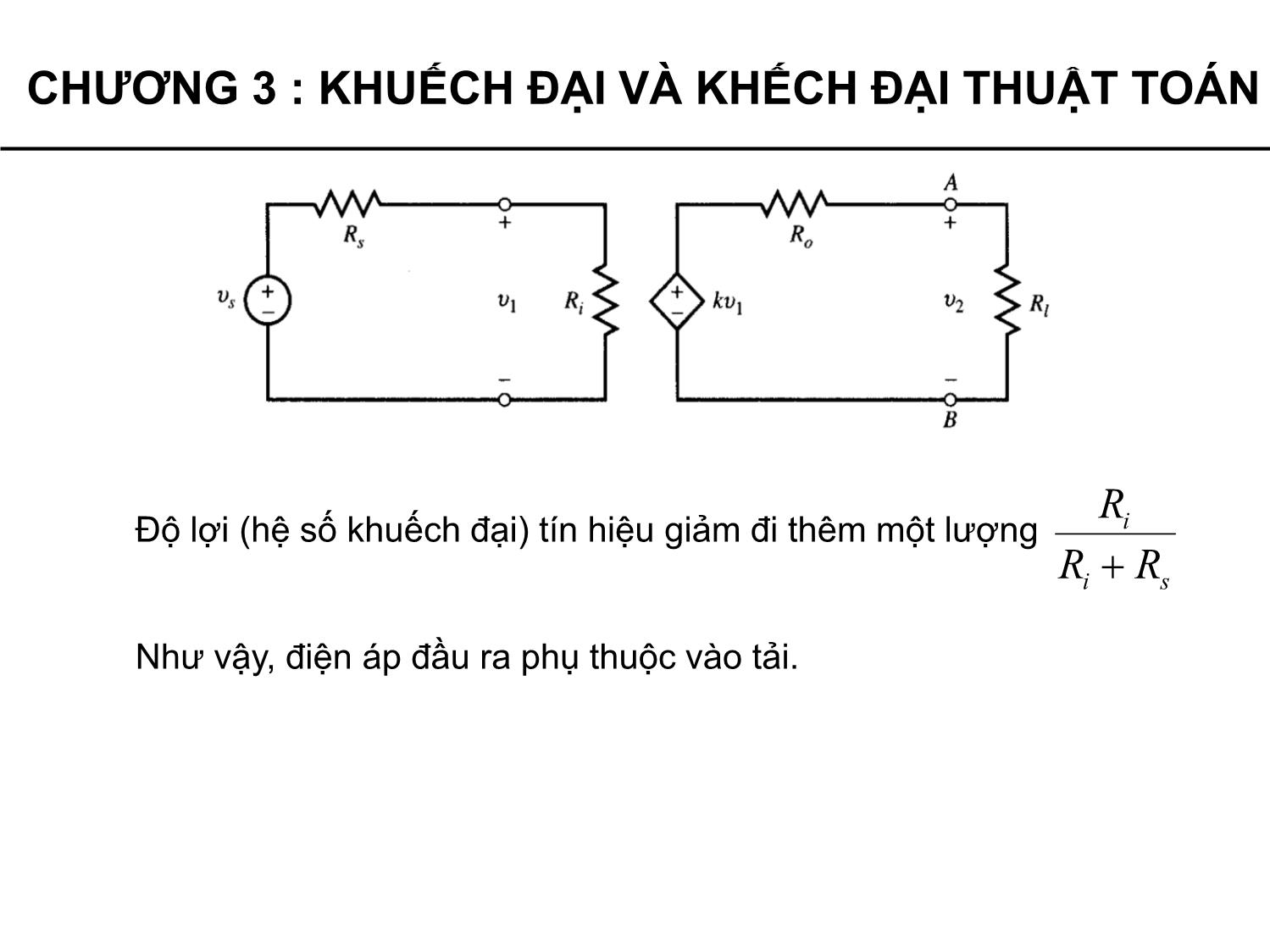
Khi đầu ra để hở mạch ta có điện áp trong đó k là hệ số
khuếch đại.
Các điện trở Ri và Ro tương ứng là điện trở vào và ra của khuếch
đại. Để hoạt động của khuếch đại tốt, các giá trị điện trở Ri cần phải
cao và R
o cần phải thấp.
Khuếch đại lý tưởng có Ri = ∞ và Ro = 0.
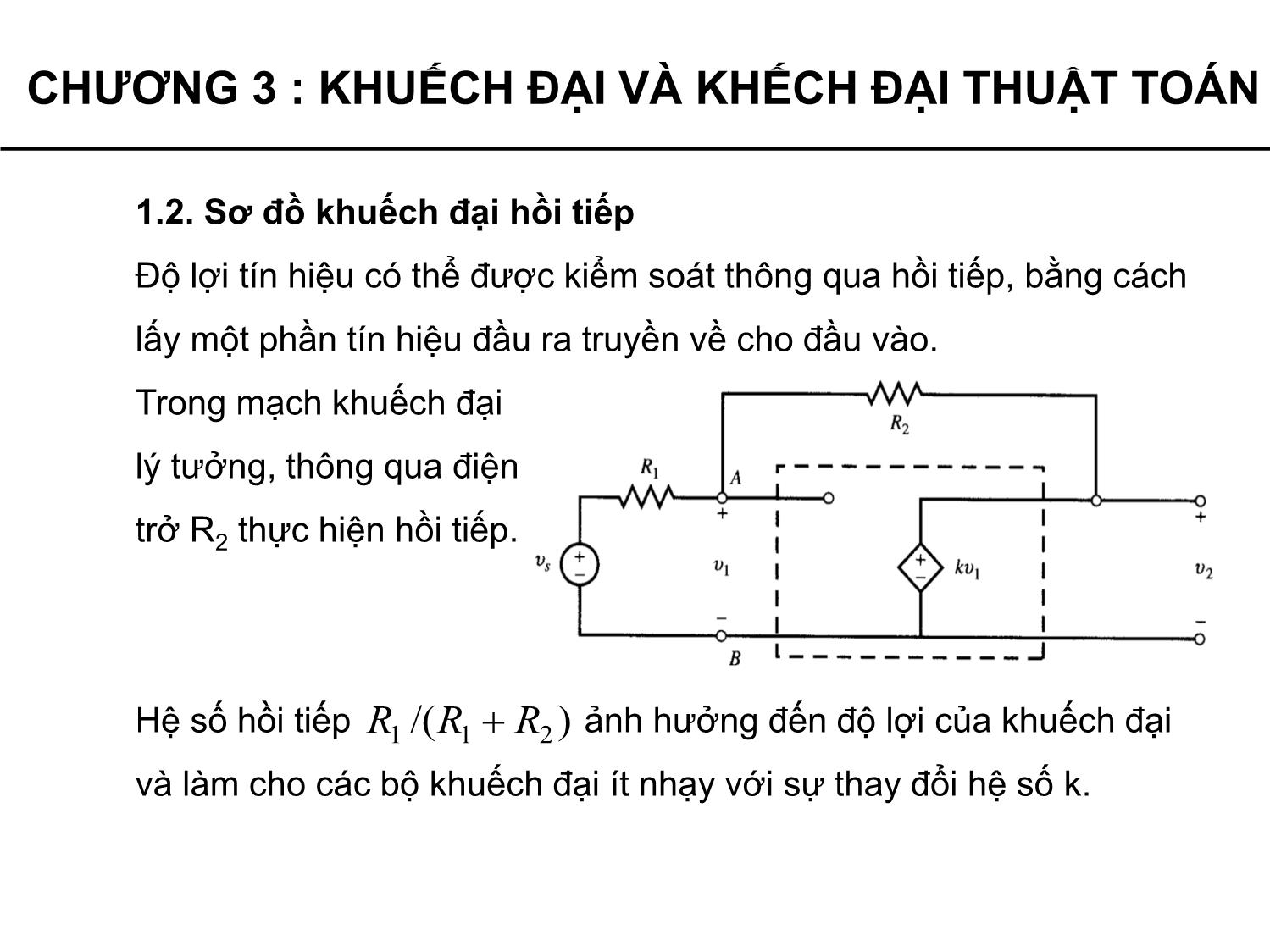
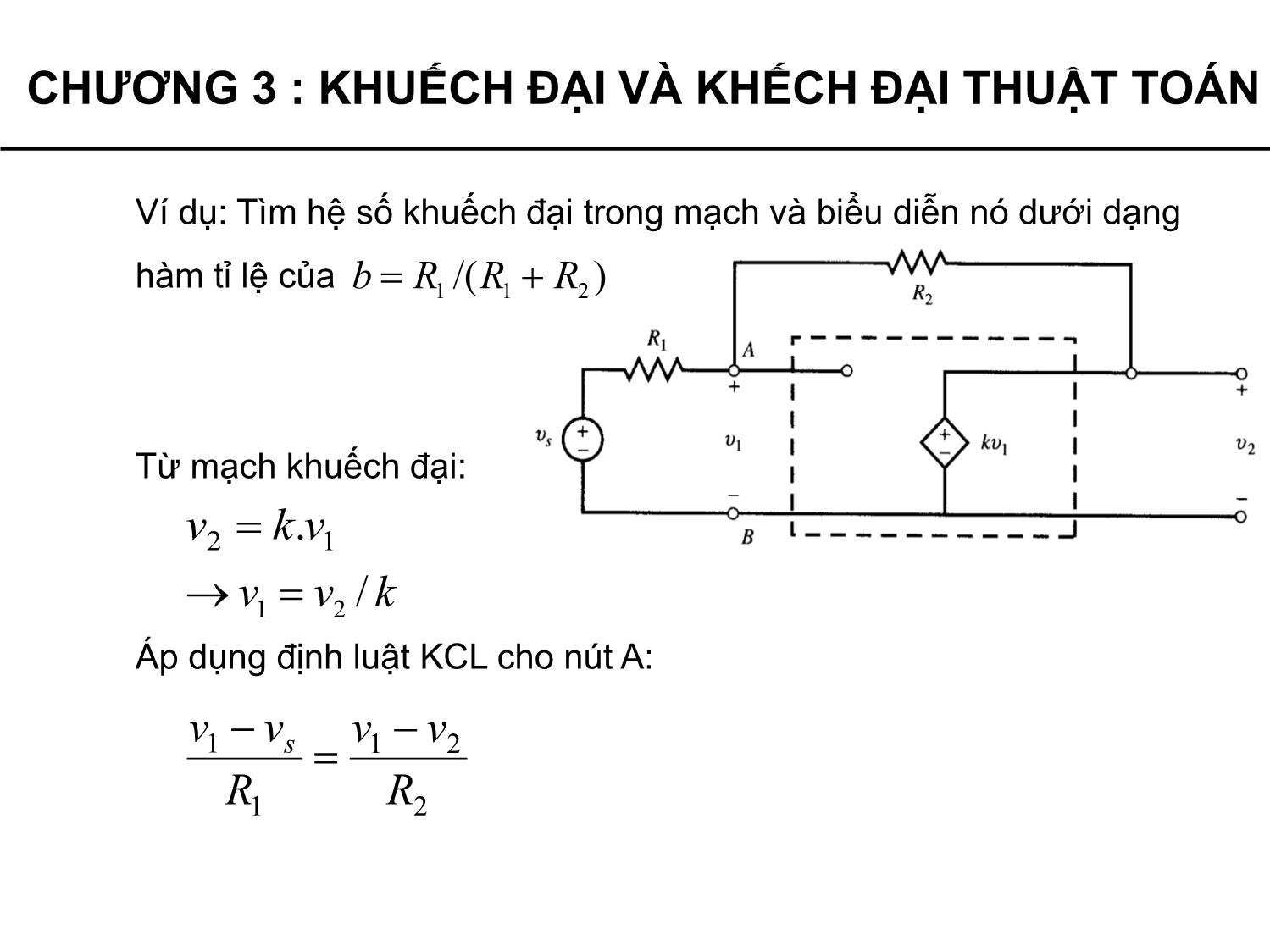
Sơ đồ khuếch đại hồi tiếp
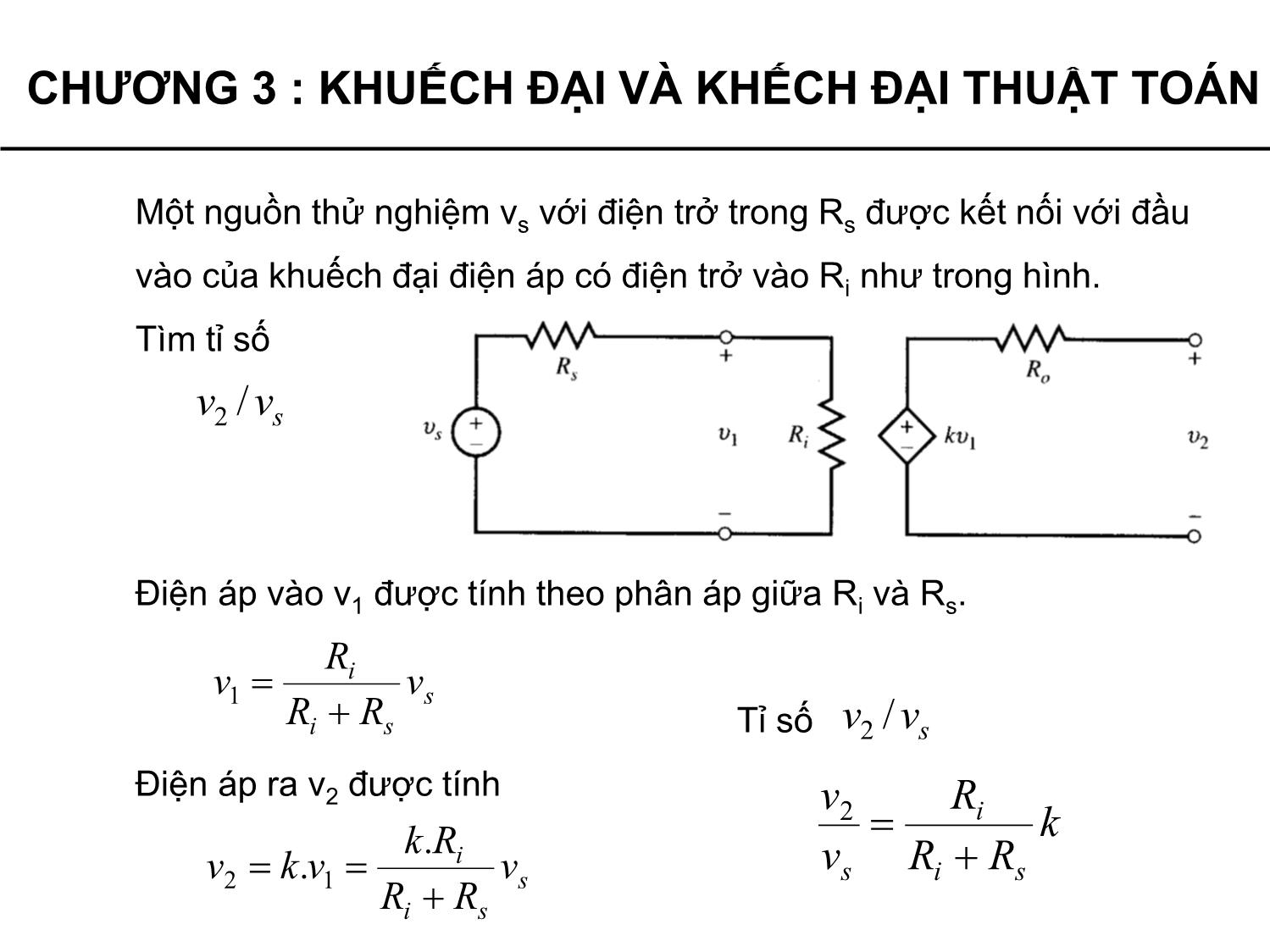
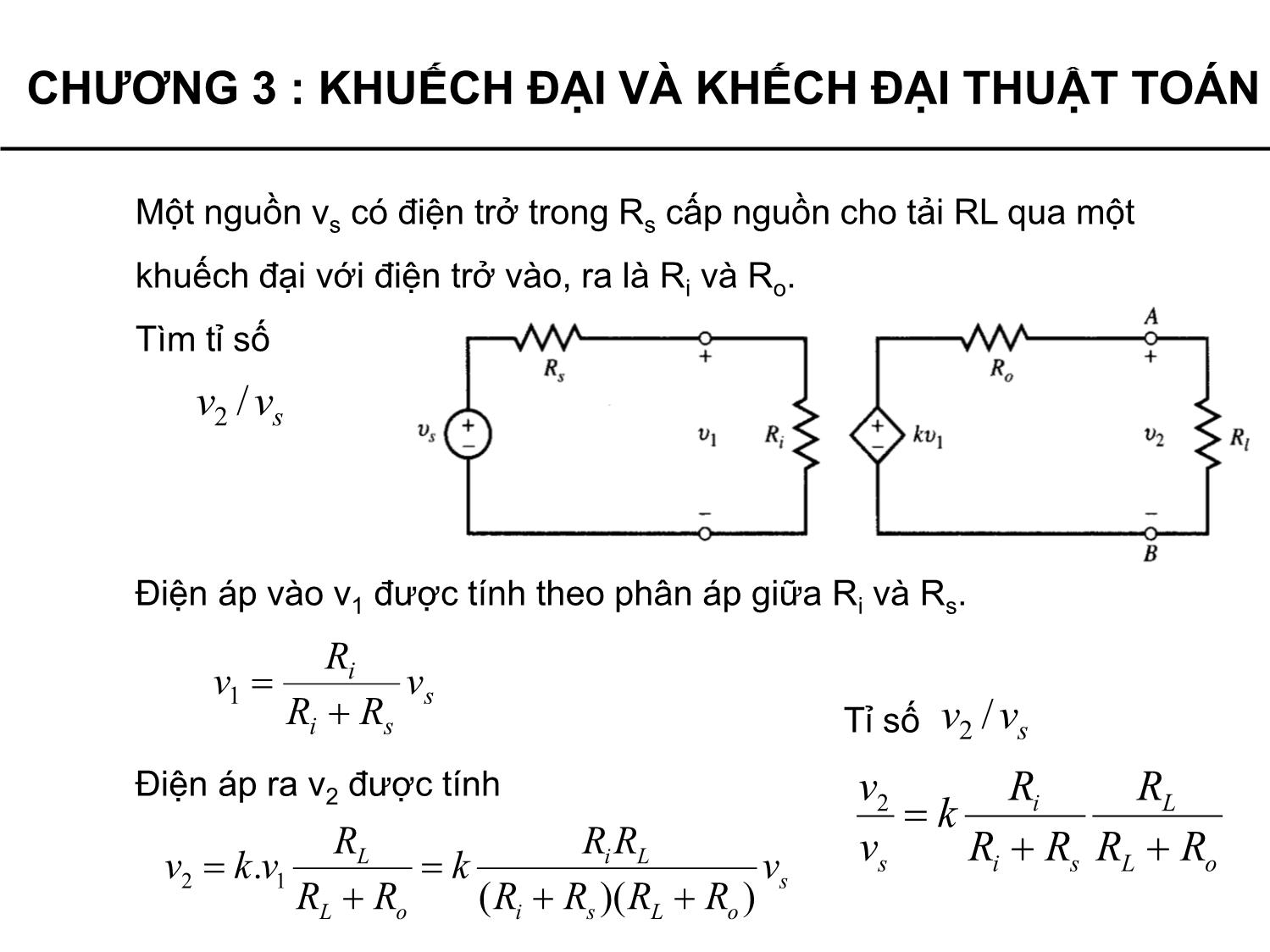
Độ lợi tín hiệu có thể được kiểm soát thông qua hồi tiếp, bằng cách
lấy một phần tín hiệu đầu ra truyền về cho đầu vào.
Trong mạch khuếch đại
lý tưởng, thông qua điện
trở R2 thực hiện hồi tiếp.
Hệ số hồi tiếp ảnh hưởng đến độ lợi của khuếch đại
và làm cho các bộ khuếch đại ít nhạy với sự thay đổi hệ số k.

Trang 1
Trang 2
Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Lý thuyết mạch - Chương 3: Mạch khuếch đại và khuếch đại thuật toán - Phạm Khánh Tùng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Lý thuyết mạch - Chương 3: Mạch khuếch đại và khuếch đại thuật toán - Phạm Khánh Tùng

không
bão hòa vB = 0. Áp dụng định luật Kirchhoff về dòng cho các nút B và
C, lưu ý dòng điện đầu vào OA (giữa cực + và cực - ) bằng không
Nút B:
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Nút B:
Nút C:
Từ hai biểu thức trên:
(b): Với vB = 0
Điện trở vào:
0
2110
2
vvvv CCC
Cvv 2,32
0
105
1 C
vv
12vvC
112 4,62,3.2 vvv 4,6/ 12 vv
5000/11 vi
5000/ 11 iv
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
(c): Với v1 = 5V, dòng điện vào
Áp dụng KCL tại nút đầu ra của OA:
Với
Công suất nguồn v1:
2,32,32 Cvv
12 1 vvC
mAi 1,05000/51
20008000
22
2
Cvvvi
mAi 5,12
Wvivp 5010.505000/ 621111
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Công suất trên các điện trở:
Tổng công suất trên các điện trở:
1000001,01000/21 Ck vp
242000242,02000/)( 222 Ck vvp
5000005,05000/215 vp k
128000128,08000/228 vp k
1000001,010000/210 Ck vp
kkkkk pppppp 1085212
100128050242010002 p
Wp 48502
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
2.3. Mạch khuếch đại đảo
Tín hiệu vào qua điện trở R1 nối trực tiếp với cổng đảo, tại cổng ra
tín hiệu hồi tiếp thông qua điện trở R2 về cổng đảo. Cổng không đảo
được tiếp đất
Để tìm hệ số khuếch đại v2/v1,
áp dụng KCL tại nút B:
Hệ số khuếch đại có giá trị âm và chỉ phụ thuộc vào các giá trị điện
trở R1 và R2. Điện trở vào của mạch là R1.
0
2
2
1
1
R
v
R
v
1
2
1
2
R
R
v
v
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
2.4. Mạch khuếch đại không đảo
Tín hiệu vào kết nối với cổng không đảo của OA. Cổng đảo nối với
đầu ra qua điện trở R2 và tiếp đất qua điện trở R1.
Để tìm hệ số khuếch đại v2/v1,
Áp dụng KCL tại nút B (nút A và B có
cùng điện thế v1 và OA không có
dòng điện):
Hệ số khuếch đại v2/v1 dương và lớn hơn 1. Điện trở vào của mạch
hữu hạn được xác định theo điều kiện dòng điện OA bằng không.
0
2
21
1
1
R
vv
R
v
1
2
1
2 1
R
R
v
v
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Ví dụ: Tìm hệ số khuếch đại v2/v1
cho sơ đồ mạch OA.
Giải
Điện thế vA được xác định từ phân
áp v1 trên điện trở 10kΩ và 5kΩ:
Từ biểu thức hệ số khuếch đại (KĐ không đảo):
Hệ số khuếch đại : v2/v1 = 1,5
11
3
1
510
5
vvvA
11
1
2
2 5,1
3
1
2
9
2
9
2
7
11 vvvvv
R
R
v AAA
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Cách 2:
Điện thế vB được xác định từ phân
áp v2 trên điện trở 7kΩ và 2kΩ:
Điện thế vA được xác định từ phân
áp v1 trên điện trở 10kΩ và 5kΩ:
Theo tính chất của OA lý tưởng vA = vB:
22
9
2
72
2
vvvB
11
3
1
510
5
vvvA
5,1
9
2
3
1
1
2
21
v
v
vv
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Ví dụ: Xác định điện áp vo từ
sơ đồ mạch OA với các điện áp
v1, v2, v3 và phần tử trong sơ đồ.
Giải
Áp dụng KCL xác định vA:
Từ biểu thức hệ số khuếch đại không đảo:
0321
R
vv
R
vv
R
vv AAA )(
3
1
321 vvvvA
321
1
2
1
2 1
3
1
1 vvv
R
R
v
R
R
v Ao
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
2.5. Mạch khuếch đại cộng tín hiệu
Cộng giá trị của các điện áp trong mạch có thể thực hiện bằng OA
trong mạch cộng tín hiệu, trường hợp mở rộng của khuếch đại đảo.
Áp dụng KCL cho nút tại cổng đảo:
0...
2
2
1
1
f
o
n
n
R
v
R
v
R
v
R
v
n
n
fff
o v
R
R
v
R
R
v
R
R
v ...2
2
1
1
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Ví dụ: Nếu trong sơ đồ mạch cộng
có 4 đầu vào với các giá trị điện trở
R1 = 1kΩ; R2 = 0,5kΩ; R3 = 0,25kΩ
và R4 = 0,125kΩ, Rf = 1kΩ. Điện áp
vào đặt một trong hai giá trị 1V và
0V. Tìm giá trị vo trong các trường
hợp điện áp v4, v3, v2, v1 nhận các
giá trị:
(a): v4 = 1V; v3 = 0V; v2 = 0V; v1 = 1V.
(b): v4 = 1V; v3 = 1V; v2 = 1V; v1 = 1V.
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Giải:
Từ biểu thức điện áp ra:
Thay các giá trị điện áp từ v4 đến v1 vào:
(a): vo = – 9V
(b): vo = –14V
Tập hợp {v4 ; v3 ; v2 ; v1} có dạng nhị phân chứa 4 bit giá trị cao (1V)
hoặc thấp (0V).
Mã nhị phân đầu vào các trường hợp (a) và (b) tương ứng là các số
nhị phân (1001)2 = (9)10 và (1110)2 = (14)10.
)248(... 12342
2
1
1
vvvvv
R
R
v
R
R
v
R
R
v n
n
fff
o
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Mạch khuếch đại cộng tín hiệu
Với các giá trị đầu vào ở mức 0V (thấp) hoặc 1V (cao), mạch khuếch
đại biến đổi giá trị nhị phân tương ứng với các tổ hợp {v4 ; v3 ; v2 ; v1}
thành điện áp âm đo bằng V trong hệ đếm cơ số 10 tương ứng.
Mạch khuếch đại tổng tín hiệu có thể làm bộ biến đổi số-tương tự.
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
2.6. Mạch lặp điện áp
Mạch OA trên có hệ số khuếch đại bằng một, trong đó v2 = v1, từ đây
ta có v1 = v
+ , v2 = v
– và v+ = v– . Điện áp ra v2 lặp lại điện áp vào v1.
Nếu nối thêm tải RL, OA gây nên ảnh hưởng của dòng tải trên RL và
điện áp nguồn. Lúc này OA làm việc như bộ đệm.
Ví dụ: (a) Tìm các giá trị: is, v1, v2 và iL trong sơ đồ mạch lặp. (b) So
sánh các kết quả tìm được với trường hợp nguồn nối trực tiếp với
tải.
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
(a): Với sơ đồ OA trên
mạch lặp, ta có:
Do mạch OA có dòng điện bằng không, nên nguồn vs được đưa đến
trực tiếp trên tải RL mà không bị suy giảm điện áp do dòng điện và
điện trở Rs. Dòng điện trên tải được cấp từ OA.
0 si
svv 1
svvv 12
L
s
L
R
v
i
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
(b): Khi loại bỏ OA trong
mạch, ta có:
Dòng điện đến RL đi qua Rs và gây nên điện áp rơi trên Rs. Điện áp
v2 phụ thuộc vào tải RL và Rs.
Ls
s
Ls
RR
v
ii
s
Ls
L v
RR
R
vv
21
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
2.7. Mạch chứa nhiều bộ khuếch đại OA
Kết quả phân tích mạch chứa một khuếch đại đơn lẻ có thể áp dụng
cho các mạch có chứa nhiều khuếch đại lý tưởng trong dạng liên
tiếp hoặc lồng nhau do không có ảnh hưởng của tải.
Ví dụ: Tìm biểu thức của điện áp v1 và v2 trong mạch hai OA
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Từ OA #1:
Và OA #2 là mạch khuếch đại tổng:
8,1)6,0(
1
3
1 v
8,2)8,1(
2
2
)5,0(
1
2
2 v
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Ví dụ: Cho Rs = 1kΩ
trong mạch OA, hãy
tìm v1, v2, vo, is, i1 và if
là hàm số của vs với
các giá trị của
(a) Rf = ∞ và (b) Rf = 40kΩ.
Giải
(a) Rf = ∞: dòng if = 0, hai bộ khuếch đại nối tiếp với v
+ = 0. Theo
mạch phân áp đầu vào ta có:
ss vvv
6
5
15
5
1
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Theo biểu thức hệ số khuếch đại của các bộ OA ta có:
(b) Rf = 40kΩ: Theo các biểu thức hệ số khuếch đại: vo = –5v2 và
v2 = –(9/5)v1, do đó vo = 9v1. Áp dụng KCL cho các dòng điện rời
khỏi nút B:
ss vvvv 5,1
6
5
5
9
5
9
12
sso vvvv 5,7)5,1(
2,1
6
2,1
6
2
s
ss
s vA
vv
ii 166,0)(
600050001000
1
0 fi
0
4051
111
os vvvvv
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Thay vo = 9v1 vào và giải theo vs:
Áp dụng KCL cho nút B:
Dòng điện i1 trên điện trở vào 5-kΩ được tạo nên bởi điện áp ra của
OA thứ hai qua điện trở hồi tiếp 40-kΩ. Dòng điện is do nguồn vs gây
nên bằng không. Điện trở vào của mạch có giá trị vô hạn.
svv 1 svvv 8,1
5
9
12
sso vvvv 9)8,1(
2,1
6
2,1
6
2
0
6000
1
vv
i ss
s
s
f vA
v
ii 2,0)(
5000
1
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
3. MẠCH KHUẾCH ĐẠI VI PHÂN – TÍCH PHÂN
3.1. Vi phân và khuếch đại vi phân
Nguồn vf không nối đất được gọi là nguồn nổi. Tín hiệu nguồn như
vậy có thể được khuếch đại thông qua mạch
Điện thế các cổng của OA
như nhau (vA = vB), nên theo
KVL ta có:
iRv f 12
12R
v
i
f
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Vì OA không có dòng điện
nên dòng đi qua R2 cũng
bằng i, áp dụng KVL, ta có:
Trường hợp đặc biệt khi hai nguồn v1 và v2 có tiếp đất chung, tương
ứng nối với cực đảo và không đảo của mạch OA, ta có vf = v1 – v2 :
022 iRiRvo
fo v
R
R
iRv
1
2
22
)()( 12
2
21
2 vv
R
R
vv
R
R
v
ll
o
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Ví dụ: Tìm biểu thức điện áp vo như hàm số của v1 và v2 trong sơ đồ
Áp dụng KCL tại nút A và B:
Do vA = vB, nên:
Nếu R3 = R1 và R2 = R4, biểu thức vo trở về dạng rút gọn ở trên
0
43
2
R
v
R
vv AA
0
21
1
R
vv
R
vv oBB
1
1
2
2
431
214
)(
)(
v
R
R
v
RRR
RRR
vo
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
3.2. Tích phân và mạch tích phân
Mạch tích phân
Thay điện trở hồi tiếp trong
mạch vi phân bằng tụ điện
ta có mạch tích phân cơ bản:
Quan hệ tín hiệu vào/ra được xác định bằng cách áp dụng KCL tại
cổng đảo:
Nói cách khác, tín hiệu ra bằng tích phân tín hiệu vào nhân với hệ số
khuếch đại – 1/RC
021
dt
dv
C
R
v
1
2 1 v
RCdt
dv
t
dtv
RC
v 12
1
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Ví dụ: Mạch điện, với R = 1kΩ, C = 1μF và v1 = sin 2000t .
Giả thiết v2(0) = 0, hãy tìm v2
với t > 0.
Giải
Điện áp ra:
t
dtv
RC
v
0
12 .
1
)12000(cos5,0.2000sin
10.10
1
0
632
tdttv
t
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Mạch tích phân Leaky
Mạch tích phân leaky, có thêm
điện trở Rf làm điện áp trên tụ
luôn được xả. Điều này làm giảm
hệ số khuếch đại và dịch góc pha
của v2.
Ví dụ: Với R = Rf = 1kΩ, C = 1μF và v1 = sin 2000t . Hãy tìm v2.
Giải
Cực đảo của OA có điện thế bằng không và tổng dòng điện đến nút
bằng không
022
1
1
fR
v
dt
dv
C
R
v
010 2
23
1
v
dt
dv
v
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Giải phương trình tìm được v2 có dạng hàm sin cùng tần số với v1
nhưng khác biệt về biên độ và góc pha:
Trong đó: A và B là các hằng số có thể xác định từ điều kiện đầu:
Thay vào phương trình vi phân
)2000cos(2 BtAv
)2000sin(20002 BtA
dt
dv
tBtABtA 2000sin)2000cos()2000sin(2
12
2310 vv
dt
dv
tBtABtA 2000sin)2000cos()2000sin(2
tBtA o 2000sin)57,262000sin(5
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Từ phương trình:
Suy ra:
Do đó:
tBtA o 2000sin)57,262000sin(5
5/5 A
oB 57,26
)57,262000cos(
5
5
2
otv
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Mạch tích phân cộng tín hiệu
Mạch khuếch đại đơn, các tín hiệu vào khác nhau kết nối với cổng
đảo và tụ điện C hồi tiếp, có thể tạo ra tổng của các tích phân các tín
hiệu với độ lợi mong muốn.
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Ví dụ: Tìm tín hiệu ra vo trong mạch khuếch đại tích phân tổng, với 3
tín hiệu vào
Áp dụng KCL tại cổng đảo
00
3
3
2
2
1
1
dt
dv
C
R
v
R
v
R
v
t
o dt
CR
v
CR
v
CR
v
v
3
3
2
2
1
1
ttt
o dtv
CR
dtv
CR
dtv
CR
v 3
3
2
2
1
1
111
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Thiết lập điều kiện đầu của tích phân (Initial Condition of
Integration)
Điều kiện đầu mong muốn
của vo, trong mạch tích phân
được thực hiện nhờ chuyển
mạch S. Đóng chuyển mạch
trong giây lát rồi lập tức ngắt
ở thời điểm t = t0, điều kiện đầu của giá trị vo được thiết lập thông
qua tụ điện và xuất hiện trên điện áp v2.
Với t > t0, giá trị của điện áp ra thêm một lượng:
o
t
vdtv
RC
v
12
1
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Mạch vi phân
Thay điện trở hồi tiếp
bằng điện cảm của
khuếch đại đảo ta có
mạch vi phân, trong đó
tín hiệu vào v1 được biến đổi thành tín hiệu ra v2.
Để xác định quan hệ vào – ra, áp dụng KCL tại nút cực đảo:
t
dtv
LR
v
2
1 1
dt
dv
R
L
v 12
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
4. MẠCH ỨNG DỤNG KHUẾCH ĐẠI THUẬT TOÁN
4.1. Mạch tính tương tự
Các mạch khuếch đại đảo, cộng và tích phân được tích hợp thành
khối ở dạng mạch tính tương tự để giải quyết các phương trình
tuyến tính. Mạch vi phân không được dùng đến do có nhiễu đáng kể.
Khi thiết kế mạch tính tương tự, trước tiên phải biến đổi các phương
trình vi phân bằng cách đưa đạo hàm bậc cao nhất hiện có của ẩn
số mang muốn về một phía của phương trình. Bổ xung các mạch
tích phân theo cấu trúc nối tiếp hoặc mạch vòng được trình bày trong
ví dụ dưới đây. Trong phần này ta sử dụng những lưu ý sau:
dtdxx /' 22'' / dtxdx
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Ví dụ: thiết kế mạch với tín hiệu vào x(t) cho tín hiệu ra y(t), thỏa
mãn phương trình sau:
Giải:
Bước 1: chuyển lại phương trình
Bước 2: Sử dụng mạch tích phân tổng tín hiệu OA#1 để lấy tích
phân hai về phương trình.
Sử dung biểu thức quan hệ vào – ra của mạch để xác định các giá trị
R1; R2; R3 và C1, theo cách tín hiệu ra của OA#1 là v1 = y’.
Ta lấy C1 = 1μF để tìm các điện trở tương ứng:
)()(3)(2)( ''' txtytyty
''' 23 yyxy
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Bước 2:
Ta lấy C1 = 1μF để tìm các điện trở:
Nhánh có tín hiệu x:
R1C1 = 1 → R1 = 1MΩ
Nhánh có tín hiệu -3y:
R2C1 = 1/3 → R2 = 333kΩ
Nhánh có tín hiệu 2y’:
R3C1 = 1/2 → R3 = 500 kΩ
''' 23 yyxy
''''
1 )23( ydtydtyyxv
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Bước 3: Lấy tích phân v1 = - y’ bằng mạch tích phân OA#2 để tìm giá
trị y. Ta lấy giá trị C2 = 1μF và R4 = 1MΩ để xác định được v2 = y, tại
đầu ra của OA#2.
ydtydtv
CR
v
'
1
24
2
1
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Bước 4: Thiết lập kết nối đầu vào cho OA#1 theo cách thức sau:
Hồi tiếp v1 = -y’ trực tiếp tới cổng đảo của OA#1 thông qua điện trở
R3.
Nối v2 = y qua bộ khuếch đại đảo bằng 1 (OA#3) để tạo ra tín hiệu
–y, sau đó cấp vào cực đảo OA#1 thông qua R2.
Kết nối nguồn x(t) vào cực đảo OA#1 thông qua điện trở R1.
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Sơ đồ hoàn chỉnh
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Bước 4: Thiết lập kết nối đầu vào cho OA#1 theo cách thức sau:
Hồi tiếp v1 = -y’ trực tiếp tới cổng đảo của OA#1 thông qua điện trở
R3.
Nối v2 = y qua bộ khuếch đại đảo bằng 1 (OA#3) để tạo ra tín hiệu
–y, sau đó cấp vào cực đảo OA#1 thông qua R2.
Kết nối nguồn x(t) vào cực đảo OA#1 thông qua điện trở R1.
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
4.2. Mạch lọc tần số thấp
Bộ khuếch đại chọn tần có hệ số khuếch đại giảm từ giá trị nhất định
xuống không tương ứng với sóng sin có tần số trong khoảng từ
không (một chiều) đến giá trị vô cùng được gọi là bộ lọc thông thấp.
Đồ thị của hệ số khuếch đại với sự thay đổi tần số được gọi là đáp
ứng tần số.
Mạch tích phân leaky cũng có thể là bộ lọc thông thấp thông qua ví
dụ sau: Mạch OA, cho v1 = sin ωt. Hãy xác định |v2| với ω = 0; 10;
100; 103; 104 và 105 rad/s.
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
Lặp lại công thức của ví dụ đã xét, đáp ứng tần số được ghi trong
bảng sau:
ω, rad/s 0 10 100 103 104 105
f, Hz 0 1,59 15,9 159 1,59.103 15,9.103
|v2/v1| 1 1 0,995 0,707 0,1 0,001
CHƯƠNG 3 : KHUẾCH ĐẠI VÀ KHẾCH ĐẠI THUẬT TOÁN
4.3. Bộ so sánh
Sơ đồ mạch so sánh điện thế v1 và điện thế tham chiếu vo. Với giá trị
rất lớn của hệ số khuếch đại, OA cho tín hiệu ra v2 ở các mức giá trị
Vcc (nếu v1 > vo) hoặc –Vcc (nếu v1 < vo). Có thể viết v2 = sgn [v1 – vo],
trong đó sgn là dấu của biểu thức trong ngoặc. Nếu vo = 0, thì ta có:
0
0
1
1
2
vV
vV
v
cc
cc
File đính kèm:
 bai_giang_ly_thuyet_mach_chuong_3_mach_khuech_dai_va_khuech.pdf
bai_giang_ly_thuyet_mach_chuong_3_mach_khuech_dai_va_khuech.pdf

