Bài giảng Lý thuyết mạch - Chương 2: Phương pháp phân tích mạch điện - Phạm Khánh Tùng
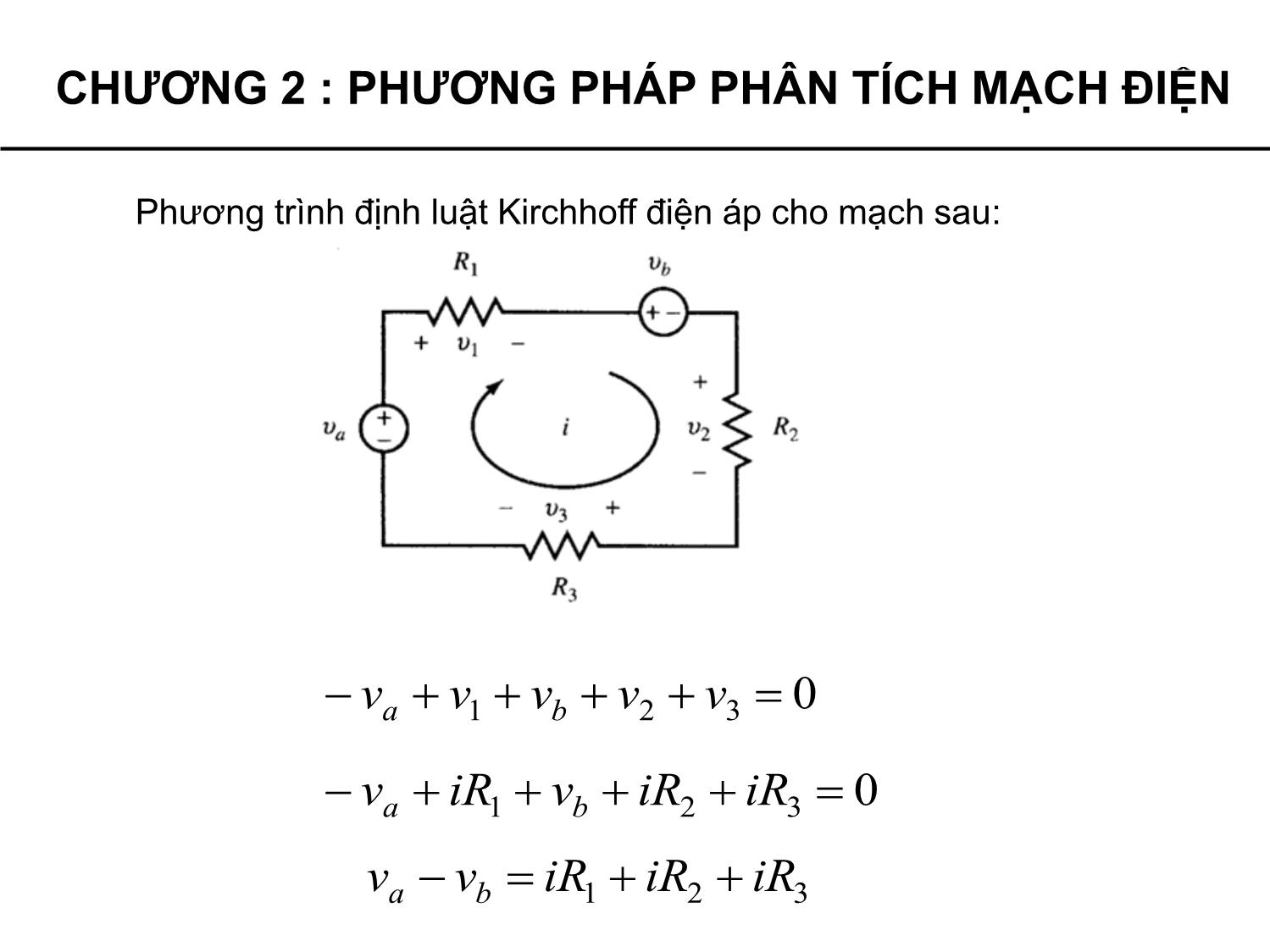
Định luật Kirchhoff về điện áp
Đối với bất kỳ vòng kín nào của mạch điện, định luật Kirchhoff về
điện áp (KA) được phát biểu: “tổng đại số của các điện áp bằng
không”.
Điện áp có thể là nguồn hoặc do dòng điện chay trên phần tử thụ
động gây nên điện áp (đôi khi còn gọi là điện áp rơi).
Định luật áp dụng tốt cho các mạch điện có nguồn không đổi, một
chiều, hoặc nguồn biến đổi theo thời gian, v(t) và i(t).
Phương pháp dòng vòng dựa trên định luật Kirchhoff về điện áp
Điểm kết nối của hai phần tử hoặc nhiều hơn được gọi là nút. Kết
nối giữa hai phần tử gọi là nút đơn, kết nối với 3 phần tử hoặc nhiều
hơn được gọi là nút chính (nút).
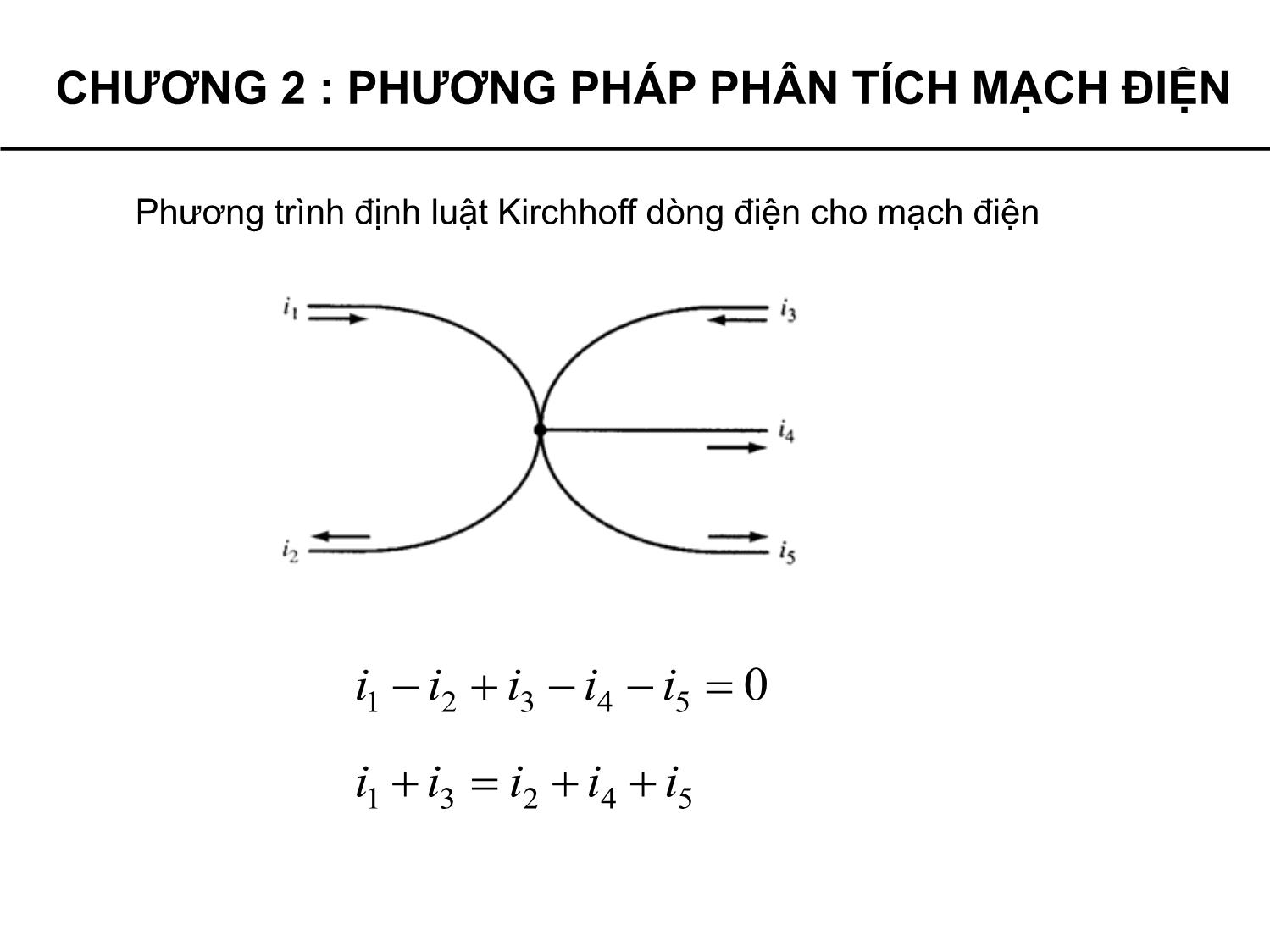
Định luật Kirchhoff về dòng điện được phát biểu: tổng đại số các
dòng điện của một nút bằng không.
Một cách phát biểu khác: tổng các dòng điện đến nút bằng tổng các
dòng điện đi khỏi nút.
Phương pháp phân tích mạch theo điện áp nút dựa trên định luật
này. Cơ sở của định luật là luật bảo toàn điện tích.

Trang 1

Trang 2
Trang 3

Trang 4
Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Lý thuyết mạch - Chương 2: Phương pháp phân tích mạch điện - Phạm Khánh Tùng

V V V I I I RRR RRR RRR CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Các phần tử của ma trận điện trở có thể định chỉ số như sau: Phần tử R12 (hàng 1, cột 2) là tổng các điện trở chung của của hai dòng mắt lưới I1 và I2 đi qua. Dấu của R12 là (+) nếu hai dòng cùng chiều trên mỗi điện trở và dấu (–) trong trường hợp ngược chiều dòng điện. Tương tự với các phần tử R21, R23, R13 và R31 là tổng các điện trở có chung hai dòng mắt lưới xác định theo chỉ số của phần tử, với dấu xác định như đối với R12. 3 2 1 3 2 1 333231 232221 131211 . V V V I I I RRR RRR RRR CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Các phần tử của ma trận điện trở có thể định chỉ số như sau: Như vậy ta có thể thấy rằng với mọi giá trị i và j, . Như vậy ta được ma trận đối xứng qua đường chéo chính. Phần tử V1 trong ma trận điện áp là tổng các nguồn dòng có trong vòng mắt lưới dẫn dòng I1. Điện áp có giá trị dương trong tổng nếu dòng đi từ cực (–) đến cực (+) của nguồn, ngược lại có dấu âm. Nguồn có dấu (+) nếu tạo ra dòng điện cùng chiều với dòng mắt lưới 3 2 1 3 2 1 333231 232221 131211 . V V V I I I RRR RRR RRR jiij RR CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Phương trình ma trận lập theo phương pháp dòng mắt lưới có thể giải theo nhiều cách khác nhau, phổ biến nhất là sử dụng định thức. Từ phương trình ma trận: Nghiệm thu được: 3 2 1 3 2 1 333231 232221 131211 . V V V I I I RRR RRR RRR 333231 23222 13121 333231 232221 131211 33323 23222 13121 1 1 / RRV RRV RRV RRR RRR RRR RRV RRV RRV I R 33331 23221 13111 2 1 RVR RVR RVR I R 33231 22221 11211 3 1 VRR VRR VRR I R CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Phương trình ma trận lập theo phương pháp dòng mắt lưới có thể giải theo nhiều cách khác nhau, phổ biến nhất là sử dụng định thức. Từ phương trình ma trận: Nghiệm thu được: 3 2 1 3 2 1 333231 232221 131211 . V V V I I I RRR RRR RRR 333231 23222 13121 333231 232221 131211 33323 23222 13121 1 1 / RRV RRV RRV RRR RRR RRR RRV RRV RRV I R 33331 23221 13111 2 1 RVR RVR RVR I R 33231 22221 11211 3 1 VRR VRR VRR I R CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Triển khai định thức tử số theo cột điện áp ta được các phương trình, qua đó có thể nhận được qui luật: Trong đó: Δij – định thức con của định thức của ma trận điện trở ΔR, trong đó loại bỏ các phần tử hàng i và cột j. RRR VVVI 313 21 2 11 11 RRR VVVI 323 22 2 12 12 RRR VVVI 333 23 2 13 13 CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 2.4. Phương pháp điện thế nút Mạch điện trong hình a có 5 nút trong đó các nút 4 và 5 là nút đơn giản còn nút 1, 2 và 3 là nút mạch. Chọn một nút mạch làm gốc, phương trình viết theo định luật KLC cho các các nút mạch còn lại. Mỗi nút mạch (trừ nút gốc) được gán một điện thế, là điện áp của nút đó so với nút gốc. Các điện thế này là ẩn số, giải các phương trình được lời giải mạch điện. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Nút 3 của mạch được gán là nút gốc, các nút 1 và 2 có điện thế V1 và V2 tương ứng. Phương trình KCL cho các nút 1,2: Định luật KCL áp dụng ở dạng này theo qui tắc dòng điện đi ra khỏi nút. Ví dụ trên nhánh 1 – 2 ở hai phương trình chiều dòng điện khác nhau 02111 CBA a R VV R V R VV 02212 E b DC R VV R V R VV CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Nếu đặt 2 phương trình ẩn V1 và V2 vào dạng ma trận, ta có: Ma trận đối xứng qua đường chéo chính. Phần tử 1,1 là tổng tất cả các nghịch đảo của điện trở nối với nút 1; phần tử 2,2 là tổng tất cả các nghịch đảo của điện trở nối với nút 2. Các phần tử 1,2 và 2,1 bằng tổng các nghịch đảo điện trở nối giữa nút 1 và 2 nhưng với dấu âm. Vế phải của phương trình là ma trận dòng điện Va/RA và Vb/RB. Cả hai giá trị đều dương bởi vì cả hai nguồn đều tạo ra dòng điện đến nút. E b A a EDCC CCBA R V R V V V RRRR RRRR 2 1 . 1111 1111 CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Ví dụ: Giải mạch điện sau bằng phương pháp điện thế nút. Giả thiết tất cả các dòng điện đều có hướng từ nút phía trên xuống nút phía dưới (nút gốc). Phương trình lập được: Nếu V1 = 10V, khi đó I1 = (10 – 20)/5 = – 2A (dấu âm cho biết dòng điện I1 đi từ nút dưới đến nút trên); I2 = (10 – 8)/2 = 1A và I3 = 10/10 = 1A. 0 2 8 105 20 111 VVV CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 3. PHÂN RÃ MẠCH ĐIỆN 3.1. Điện trở vào và điện trở ra Mạch điện đơn nguồn hình bên trong đó nguồn áp được gọi là V1 và tương ứng là dòng điện I1. Nếu chỉ có một nguồn duy nhất V1, phương trình đối với I1 như sau: Trong đó: ΔR – định thức ma trận điện trở lập theo phương pháp dòng mắt lưới. Δ11 – định thức con khi loại bỏ hàng và cột có chỉ số tương ứng với mắt lưới có nguồn áp. R VI 1111 CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Điện trở vào của mạch là tỉ số giữa điện áp V1 và dòng điện I1: Trong đó: ΔR – định thức ma trận điện trở lập theo phương pháp dòng mắt lưới. Δ11 – định thức con khi loại bỏ hàng và cột có chỉ số tương ứng với mắt lưới có nguồn áp. 111 1 1. Rinput I V R CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 3.2. Điện trở chuyển đổi Nguồn áp kết nối với bất cứ phần nào của mạch điện đều tạo ra dòng điện trên tất cả các nhánh. Ví dụ, nguồn áp nối vào mạch thụ động tạo ra dòng điện đầu ra của mạch nơi có tải điện trở nối vào. Trong trường hợp này, mạch điện có hệ số chuyển đổi điện trở qua toàn mạch. Xét mạch thụ động hình bên, một nguồn nối vào ký hiệu là Vr tạo ra dòng điện phía đầu ra Is. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Quan hệ giữa dòng điện Is và điện áp Vr qua thông số của mạch thụ động (không nguồn). Nếu cần tính dòng điện Is theo điện áp Vr (nguồn áp duy nhất), sử dụng phương trình ma trận dòng mắt lưới để tính dòng Is trong biểu thức chỉ có một thành phần duy nhất liên quan đến Vr: ...00...)0( 1 R rs r R s s VI R rs rs VI CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Lấy tỉ số giữa Vr và Is chính là điện trở chuyển đổi của mạch điện: Ma trận điện trở lập theo phương pháp dòng vòng là đối xứng qua đường chéo chính Δrs = Δsr. Biểu thức này cho thấy một tính chất quan trong của mạch tuyến tính: Nếu một nguồn áp ở mắt lưới r tạo ra dòng điện ở mắt lưới s, thì cũng nguồn đó ở mắt lưới s cũng tạo ra chính dòng điện có trị số không đổi trong mắt r. rs R s r rstransfer I V R . srtransferrstransfer RR .. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Xét trường hợp tổng quát với mạch n mắt lưới chứa một số nguồn nhất định. Dòng điện trong mắt lưới k được tính theo biểu thức: Biểu thức dòng điện cho thấy rõ nguyên lý chồng chất, cho thấy các điện trở ảnh hưởng đến sự tác động của các nguồn trên một mắt lưới cụ thể. Nguồn cách xa mắt lưới k sẽ có điện trở chuyển đổi đến mắt lưới lớn dẫn đến dòng điện do nguồn đó tạọ ra là thành phần nhỏ trong dòng điện tổng Ik. Nguồn Vk, và các nguồn khác ở mắt lưới lân cận sẽ cho thành phần dòng điện lớn hơn trong Ik. nktf n kktf k kinput k kktf k ktf k R V R V R V R V R V I .)1.( 1 .)1.( 1 1. 1 ...... CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 3.3. Qui tắc phân rã mạch điện Phương pháp dòng mắt lưới và điện thế nút là các kỹ thuật chính để phân tích mạch điện. Tuy nhiên, điện trở tương đương của các nhánh nối tiếp hoặc song song kết hợp với các quy tắc phân chia điện áp và dòng điện tạo nên một phương pháp phân tích mạch khác. Phương pháp này thường phải vẽ lại hoặc thêm một số mạch điện bổ xung thậm chí đơn giản hóa mạch điện dẫn đến những mạch rất đơn giản, có thể tính dễ dàng dòng, áp và công suất. Phân rã mạch điện bắt đầu bằng việc tìm kiến các cụm điện trở nối tiếp và song song. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Ví dụ: Tính tổng công suất cung cấp từ nguồn 60V và công suất trên mỗi điện trở của mạch điện 1257 abR 4 612 6.12 cdR 3 124 12.4 efR 1073 tđR CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Tổng công suất trên các điện trở bằng tổng công suất nguồn: Công suất nguồn chia trên 2 điện trở Ref và Rge: Công suất Pef chia trên hai điện trở Rcd và Rab: 360 10 6022 tđ T R V P 252 37 7 7 Tge PPP 108 37 3 3 Tef PPP 81 412 12 efcd PP 27 412 4 efab PP CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Công suất trên các điện trở riêng rẽ là: 27 612 6 12 cdPP 75,15 57 7 7 abPP 54 612 12 6 cdPP 25,11 57 5 5 abPP CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 3.4. Qui tắc xếp chồng Mạch tuyến tính có nhiều nguồn độc lập có thể phân tích tìm giá trị dòng, áp bằng cách xét tác động riêng rẽ của từng nguồn và xếp chồng các kết quả. Nguyên tắc này dựa trên tính chất tuyến tính quan hệ dòng và áp nhưng không áp dụng được khi tính công suất, do công suất tỉ lệ với bình phương dòng hoặc áp, và quan hệ này là không tuyến tính. Với nguồn phụ thuộc, xếp chồng chỉ được áp dụng khi các thông số điều khiển nguồn nằm bên ngoài mạch chứa nguồn đang xét. Các nguồn còn lại khi xét tác động của một nguồn được thay thế như sau: nguồn áp bị nối tắt và nguồn dòng bị hở mạch CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Ví dụ, biểu thức tính dòng của mạch theo phương pháp mắt lưới: Vế phải là tổng của 3 thành phần tạo nên dòng điện I1, nếu chỉ có nguồn trên một vòng mắt lưới, các vòng còn lại không có nguồn thì dòng điện I1 chỉ có một thành phần. Ví dụ: Hãy tính dòng điện trên điện trở 23Ω của mạch trong hình bằng phương pháp xếp chồng. Triệt tiêu lần lượt nguồn dòng 20A rồi nguồn áp 200V RRR VVVI 313 21 2 11 11 CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Triệt tiêu lần lượt nguồn dòng 20A Điện trở tương đương của mạch: 5,60 23427 )234(27 47 tđR 31,3 5,60 200 TI 65,131,3 54 27' 23 I CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Triệt tiêu lần lượt nguồn áp 200V Điện trở tương đương của mạch: Dòng điện tổng trên điện trở 23Ω: 15,21 4727 47.27 4 tđR 58,920 2315.21 15.21'' 23 I 23,1158,965,1''23 ' 2323 III CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 4. ĐỊNH LÝ MẠCH ĐIỆN 4.1. Định lý Thevenin và Norton Mạch tuyến tính có một hoặc nhiều nguồn áp, dòng có thể được thay thế bằng một nguồn áp nối tiếp điện trở (định lý Thevenin) hoặc một nguồn dòng song song điện trở (định lý Norton). Nguồn áp được gọi là nguồn áp tương đương Thevenin, V’ và nguồn dòng được gọi là nguồn dòng tương đương Norton, I’. Hai điện trở trong nguồn áp Thevenin và nguồn dòng Norton hoàn toàn như nhau, R’. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Khi hai cực ab trên hình (a) hở mạch, xuất hiện điện áp giữa chúng hình (b), và phải bằng V’ của sơ đồ tương đương Thevenin. Nếu giữa hai cực ab ngắn mạch ở hình (a) (đường nét đứt) xuất hiện dòng điện, bằng dòng điện tương đương Norton hình (c). Như vậy sơ đồ mạch trên hình (b) và (c) tương đương với cùng mạch điện hình (a), thì chúng tương đương với nhau. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Điện trở R’ là điện trở của mạch khi bỏ hết các nguồn, điện trở tương đương giữa hai cực a và b: Khi ngắn mạch tại các cực ab, dòng điện ngắn mạch Isc do hai nguồn gây nên, xếp chồng các kết quả: 5 9 6.3 3' R 2 6 3.3 6 10 33 3 9 6.3 3 20 36 6' IIsc CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Ví dụ: Hãy tính mạch tương đương Thevenin và Norton cho mạch Khi ab hở mạch, hai nguồn áp tạo thành mạch kín có dòng điện qua các điện trở 3Ω và 6Ω Điện áp tương đương Thevenin: 9 30 36 1020 I 103 9 30 20' VVab 10106 9 30' VVab CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN Sơ đồ mạch điện tương đương Thevenin và Norton với các giá trị V’, R’ và I’ được tính riêng biệt. Theo định luật Ohm, nếu biết hai trong số đó có thể tìm được giá trị thứ ba. Các định lý Thevenin và Norton rất hữu dụng khi khảo sát mạch điện với số lượng lớn các tải khác nhau. Sử dụng sơ đồ nguồn áp hoặc nguồn dòng tương đương kết nối lần lượt các tải ta có thể dễ dàng tính được các giá trị dòng áp, công suất trên tải. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 4.2. Định lý truyền công suất cực đại Giả thiết mạch có nguồn là tuyến tính, có thể phân rã thành mạch điện dưới đây: Khi đó: Công suất tiêu thụ trên điện trở: Trong biểu thức của PL đạt giá trị tối đa khi RL = R’, trong trường hợp đó công suất trên R’ cũng là có giá trị Do đó hiệu suất truyền tải đạt cực đại 50 %. LRR V I ' ' 2 ' ' ' 2' 2' 2' 1 4)( L L L L L RR RR R V R RR V P '2' 4/ RV '2' 4/ RV CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.1: Xác định giá trị nguồn áp V3 và cực tính nếu như dòng điện I trong hình có giá trị bằng 0,4 A. Bài 2.2: Xác định điện trở tương đương của mạch CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.3: Xác định giá trị tương đương của mạch ba điện cảm mắc song song Bài 2.4: Hãy tính điện dung tương đương của mạch điện CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.5: Mạch điện trên hình bên là mạch phân áp. Hãy xác định tỉ số đối với một số giá trị điện trở R sau đây: a) R = ∞; b) R = 1 MΩ; c) R = 10 kΩ; và d) R = 1 kΩ. Bài 2.6: Xác định dòng điện trên các nhánh của mạch điện CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.5: Mạch điện trên hình bên là mạch phân áp. Hãy xác định tỉ số đối với một số giá trị điện trở R sau đây: a) R = ∞; b) R = 1 MΩ; c) R = 10 kΩ; và d) R = 1 kΩ. Bài 2.6: Xác định dòng điện trên các nhánh của mạch điện CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.7: Sử dụng phương pháp dòng nhánh trong mạch điện hình bên để xác định dòng điện của nguồn áp 6V gây nên. Bài 2.8: Giải bài 2.7 bằng phương pháp dòng mắt lưới CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.9: Phân tích mạch điện trong bài 2.7 và 2.8 bằng phương pháp điện thế nút: Bài 2.10: Trong bài 2.8, xác định điện trở vào (Rin) từ nhánh 1, từ đó tính dòng I1. Bài 2.11: Trong bài 2.8 xác định các điện trở chuyển đổi Rtf,12 và Rtf,13 từ đó tính dòng điện I2 và I3. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.12: Giải mạch bài 2.7 theo phương pháp dòng vòng với các vòng xác định theo hình vẽ. Bài 2.13: Viết phương trình ma trận dòng mắt lưới cho mạch điện sơ đồ hình dưới và giải để tìm dòng điện. CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.14: Giải mạch điện hình bên bằng phương pháp điện thế nút Bài 2.15(33): Cho mạch điện trong hình bên. Hãy xác định Vs để dòng điện có giá trị I0 = 7,5 mA CHƯƠNG 2 : PHƯƠNG PHÁP PHÂN TÍCH MẠCH ĐIỆN 5. BÀI TẬP Bài 2.14: Giải mạch điện hình bên bằng phương pháp điện thế nút Bài 2.15: Cho mạch điện trong hình bên. Hãy xác định Vs để dòng điện có giá trị I0 = 7,5 mA
File đính kèm:
 bai_giang_ly_thuyet_mach_chuong_2_phuong_phap_phan_tich_mach.pdf
bai_giang_ly_thuyet_mach_chuong_2_phuong_phap_phan_tich_mach.pdf

