Bài giảng Kỹ thuật số - Chương 4: Mạch logic - Đặng Ngọc Khoa
Biểu diễn bằng biểu thức đại số
Một hàm logic n biến bất kỳ luôn có thể
biểu diễn dưới dạng:
Tổng của các tích (Chuẩn tắc tuyển - CTT):
là dạng tổng của nhiều thành phần mà mỗi
thành phần là tích của đầy đủ n biến.
Tích của các tổng (Chuẩn tắc hội – CTH): là
dạng tích của nhiều thành phần mà mỗi
thành phần là tổng của đầy đủ n biến.
Rút gọn mạch logic
Làm cho biểu thức logic đơn giản nhất và do
vậy mạch logic sử dụng ít cổng logic nhất.
Hai mạch sau đây là tương đương nhau
Trang 1

Trang 2

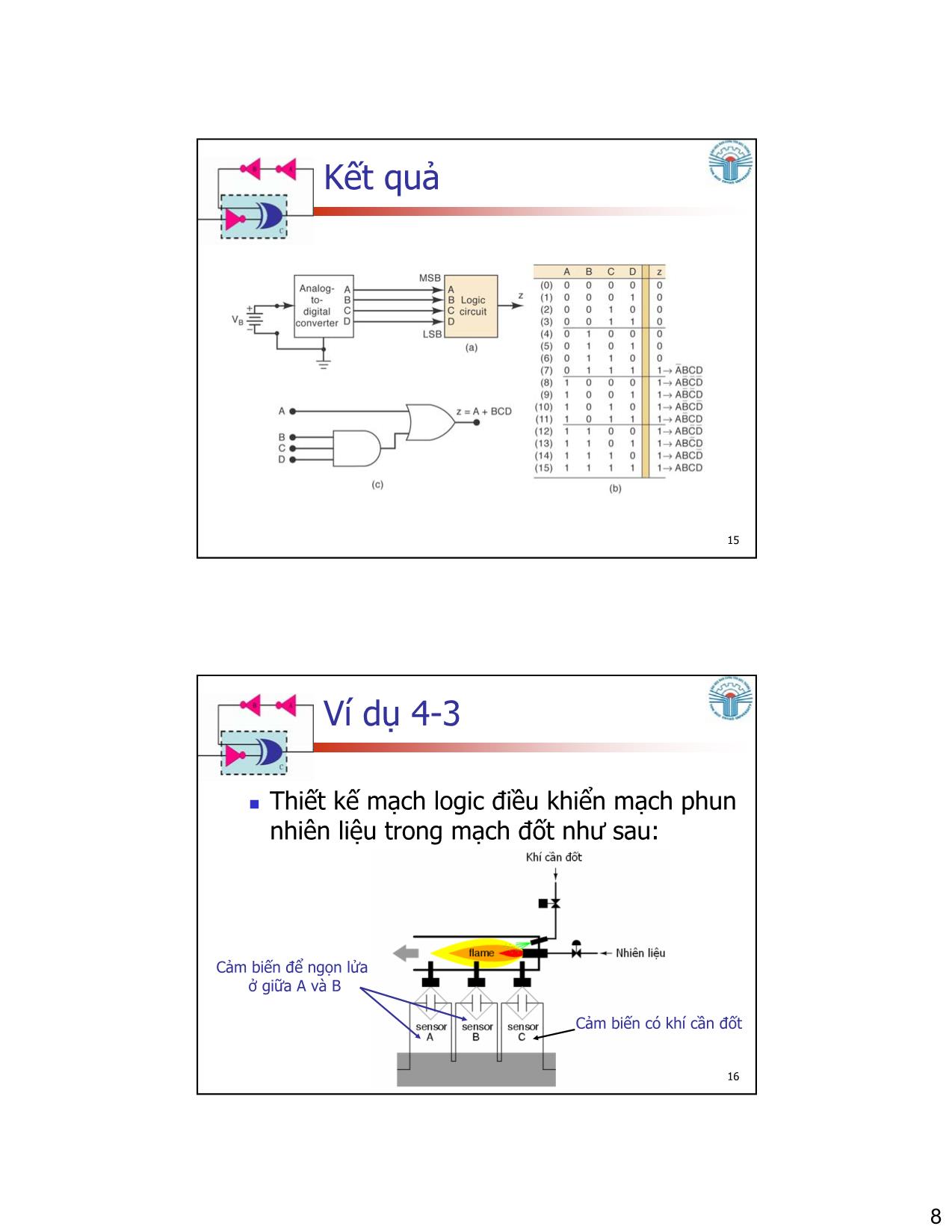
Trang 3
Trang 4

Trang 5

Trang 6

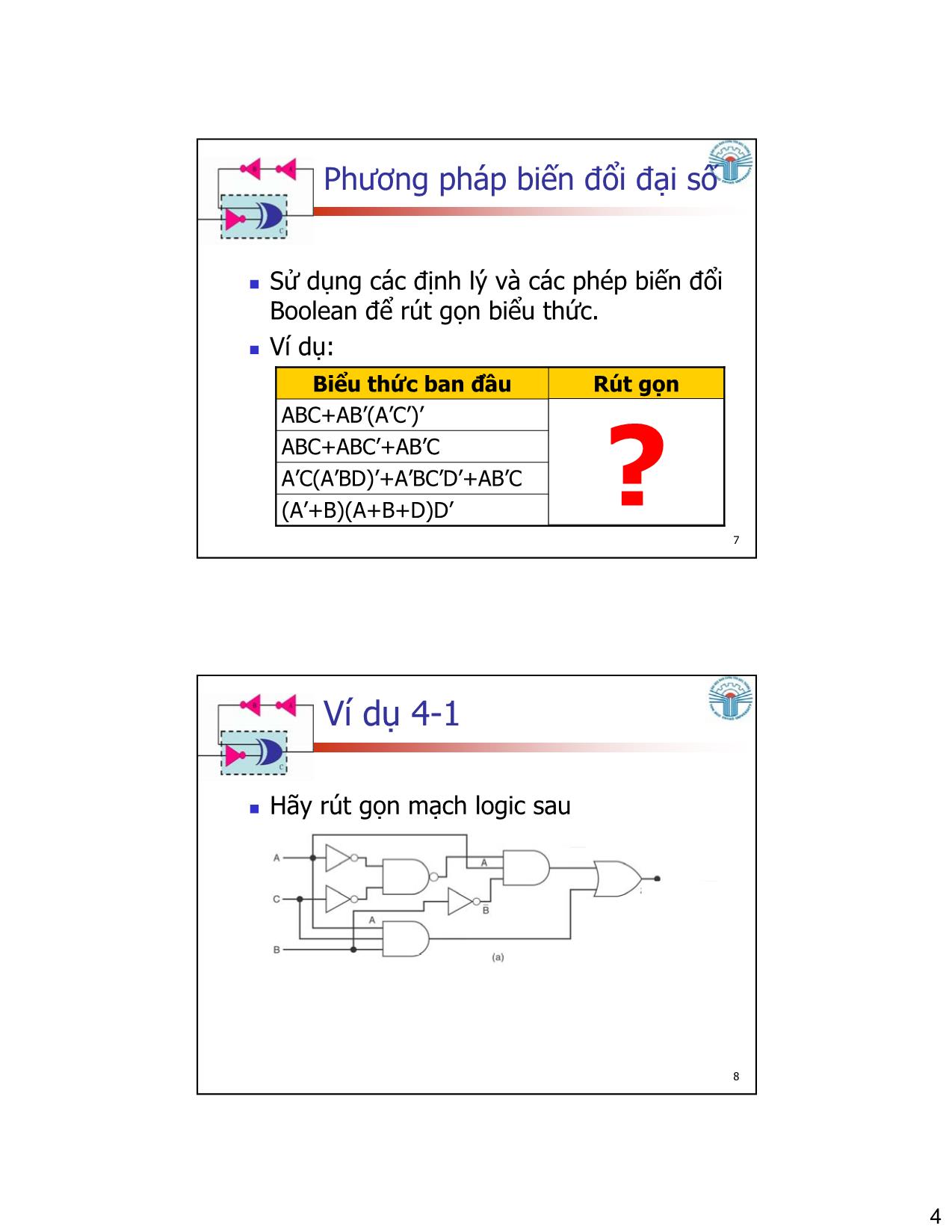
Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kỹ thuật số - Chương 4: Mạch logic - Đặng Ngọc Khoa", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật số - Chương 4: Mạch logic - Đặng Ngọc Khoa
11 Chương 4 Mạch logic Th.S Đặng Ngọc Khoa Khoa Điện - Điện Tử 2 Biểu diễn bằng biểu thức đại số Một hàm logic n biến bất kỳ luôn có thể biểu diễn dưới dạng: Tổng của các tích (Chuẩn tắc tuyển - CTT): là dạng tổng của nhiều thành phần mà mỗi thành phần là tích của đầy đủ n biến. Tích của các tổng (Chuẩn tắc hội – CTH): là dạng tích của nhiều thành phần mà mỗi thành phần là tổng của đầy đủ n biến. 23 Dạng chuẩn tắc tuyển F=ABC+ ABC + ABC + ABC Dạng chuẩn tắc hội F = (A+B+C)(A+B+C)(A+B+C)(A+B+C) Biểu diễn bằng biểu thức đại số ∑= )6,5,2,1(FA B C F 0 0 00 00 000 0 0 0 0 0 1 1 11 1 11 1 1 0 111 11 0 1 1 0 3 2 1 4 7 6 5 Vị trí ∏= )7,4,3,0(F 4 Biểu diễn bằng biểu thức đại số X = 1 ghi XX = 1 ghi X X = 0 ghi XX = 0 ghi X Lưu ý các giá trị 0Lưu ý các giá trị 1 Tích của các tổngTổng của các tích Chuẩn tắc hộiChuẩn tắt tuyển ∑ ∏ 35 Rút gọn mạch logic Làm cho biểu thức logic đơn giản nhất và do vậy mạch logic sử dụng ít cổng logic nhất. Hai mạch sau đây là tương đương nhau 6 Phương pháp rút gọn Có hai phương pháp chính để rút gọn một biểu thức logic. Phương pháp biến đổi đại số: sử dụng các định lý và các phép biến đổi Boolean để rút gọn biểu thức. Phưong pháp bìa Karnaugh: sử dụng bìa Karnuagh để rút gọn biểu thức logic 47 Phương pháp biến đổi đại số Sử dụng các định lý và các phép biến đổi Boolean để rút gọn biểu thức. Ví dụ: BD’(A’+B)(A+B+D)D’ B’C+A’D’(B+C)A’C(A’BD)’+A’BC’D’+AB’C A(B+C)ABC+ABC’+AB’C A(B’+C)ABC+AB’(A’C’)’ Rút gọnBiểu thức ban đầu ? 8 Ví dụ 4-1 Hãy rút gọn mạch logic sau 59 Bài toán thiết kế Hãy thiết kế một mạch logic có: Ba ngõ vào Một ngõ ra Ngõ ra ở mức cao chỉ khi đa số ngõ vào ở mức cao 10 Trình tự thiết kế Bước 1: Thiết lập bảng chân trị. 1111 1011 1101 0001 1110 0010 0100 0000 xCBA Mạch logic A B C x 611 Trình tự thiết kế Bước 2: Thiết lập phương trình từ bảng chân trị. 1111 1011 1101 0001 1110 0010 0100 0000 xCBA A.B.C A.B.C A.B.C A.B.C ABCCABCBABCAx +++= 12 Trình tự thiết kế Bước 3: Rút gọn biểu thức logic ABACBCx ABCCABABCCBAABCBCAx ABCCABCBABCAx ++= +++++= +++= 713 Trình tự thiết kế Bước 4: Vẽ mạch logic ứng với biểu thức logic vừa rút gọn ABACBCx ++= 14 Ví dụ 4-1 Hãy thiết kế một mạch logic có 4 ngõ vào A, B, C, D và một ngõ ra. Ngõ ra chỉ ở mức cao khi điện áp (được miêu tả bởi 4 bit nhị phân ABCD) lớn hơn 6. 815 Kết quả 16 Ví dụ 4-3 Thiết kế mạch logic điều khiển mạch phun nhiên liệu trong mạch đốt như sau: Cảm biến có khí cần đốt Cảm biến để ngọn lửa ở giữa A và B 917 Bìa Karnaugh 18 Phương pháp bìa Karnaugh Giống như bảng chân trị, bìa Karnaugh là một cách để thể hiện mối quan hệ giữa các mức logic ngõ vào và ngõ ra. Bìa Karnaugh là một phương pháp được sử dụng để đơn giản biểu thức logic. Phương pháp này dễ thực hiện hơn phương pháp đại số. Bìa Karnaugh có thể thực hiện với bất kỳ số ngõ vào nào, nhưng trong chương trình chỉ khảo sát số ngõ vào nhỏ hơn 6. 10 19 Định dạng bìa Karnaugh Mỗi một trường hợp trong bảng chân trị tương ứng với 1 ô trong bìa Karnaugh Các ô trong bìa Karnaugh được đánh số sao cho 2 ô kề nhau chỉ khác nhau 1 giá trị. Do các ô kề nhau chỉ khác nhau 1 giá trị nên chúng ta có thể nhóm chúng lại để tạo một thành phần đơn giản hơn ở dạng tổng các tích. 20 Bảng chân trị ⇒ K-map Y 0 1 0 1 Z 1 0 1 1 X 0 0 1 1 Giá trị 0 Î Giá trị 1 Î Giá trị 2 Î Giá trị 3 Î 1 1 0 1 Một ví dụ tương ứng giữa bảng chân trị và bìa Karnaugh 0 1 2 3 Y Y X XZ 11 21 Y Y X X 0 0 1 0 X Y Y Y X X 0 0 0 1 X Y Y Y X X 1 0 0 0 X Y Y Y X X 0 1 0 0 X Y Xác định giá trị các ô 22 Nhóm các ô kề nhau X Y Y Y X X 1 0 1 0 X Y YY Y X X 1 0 1 0 Z = X Y + X Y = Y ( X + X ) = Y 12 23 Nhóm các ô lại với nhau Nhóm 2 ô “1” kề nhau, loại ra biến xuất hiện ở cả hai trạng thái bù và không bù. Nhóm 4 ô “1” kề nhau, loại ra 2 biến xuất hiện ở cả hai trạng thái bù và không bù. Nhóm 8 ô “1” kề nhau, loại ra 3 biến xuất hiện ở cả hai trạng thái bù và không bù. 24 Y Y X X 1 1 0 0 XY Y X X 1 0 1 0 Y K-map 2 biến: nhóm 2 Y Y X X 0 1 0 1 Y Y Y X X 0 0 1 1 X 13 25 Y Y X X 1 1 1 1 1 K-map 2 biến: nhóm 4 26 Ví dụ K-map 2 biến S 0 1 0 1 T 1 0 1 0 R 0 0 1 1 1 0 1 0 T = F(R,S) = S S S S R R 0 1 2 3 T 14 27 K-map 3 biến 0 Î 1 Î 2 Î 3 Î 4 Î 5 Î 6 Î 7 Î C 0 1 0 1 0 1 0 1 Y 1 0 1 1 0 0 1 0 B 0 0 1 1 0 0 1 1 A 0 0 0 0 1 1 1 1 1 0 1 1 1 0 0 0 0 1 2 3 6 7 4 5 C C A B A B A BA BY 28 K-map 3 biến: nhóm 2 C C A B A B A BA B 0 0 0 0 0 1 0 1 A C 1 0 B 1 B 0 111 1 15 29 K-map 3 biến: nhóm 4 C C A B A B A BA B 0 0 0 0 1 1 1 1 A 1 1 0 0 B 1 0 C 1 0 B 30 K-map 3 biến: nhóm 8 C C A B A B A BA B 1 1 1 1 1 1 1 1 1 16 31 Bìa Karnaugh 4 biến 01111 00111 11011 00011 11101 00101 01001 10001 01110 10110 01010 10010 01100 00100 01000 10000 FDCBA AB CD 00 01 11 10 00 01 11 10 F 32 Bìa Karnaugh 4 biến AB CD 00 01 11 10 00 01 11 10 F Lưu ý các ký hiệu trong bìa Karnaugh 17 33 Bìa Karnaugh 4 biến 0 0 0 1 1 0 0 1 0 0 1 0 0 1 0 1 01111 00111 11011 00011 11101 00101 01001 10001 01110 10110 01010 10010 01100 00100 01000 10000 FDCBA AB CD 00 01 11 10 00 01 11 10 F 34 K-map 4 biến: nhóm 2 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 AB CD 00 01 11 10 00 01 11 10 F ACD BCD 18 35 K-map 4 biến: nhóm 4 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 AB CD 00 01 11 10 00 01 11 10 F CD 36 K-map 4 biến: nhóm 4 0 0 0 0 0 1 1 0 0 1 1 0 0 0 0 0 AB CD 00 01 11 10 00 01 11 10 F BD 19 37 K-map 4 biến: nhóm 4 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 AB CD 00 01 11 10 00 01 11 10 F BC 38 K-map 4 biến: nhóm 4 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 1 AB CD 00 01 11 10 00 01 11 10 F BD 20 39 K-map 4 biến: nhóm 8 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 AB CD 00 01 11 10 00 01 11 10 F B 40 K-map 4 biến: nhóm 8 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 AB CD 00 01 11 10 00 01 11 10 F A 21 41 K-map 4 biến: nhóm 8 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 AB CD 00 01 11 10 00 01 11 10 F B 42 Rút gọn bằng bìa Karnaugh Bước 1: Biểu diễn hàm đã cho trên bìa Karnaugh. Bước 2: Nhóm các ô có giá trị bằng 1 theo các quy tắc: Tổng các ô là lớn nhất. Tổng các ô phải là 2n (n nguyên). Các ô này phải nằm kề nhau. 22 43 Rút gọn bằng bìa Karnaugh Bước 3: Làm lại bước 2 cho đến khi tất cả các ô logic 1 đều được sử dụng. Bước 4: Xác định kết quả theo các quy tắc: Mỗi nhóm sẽ là một tích của các biến. Kết quả là tổng của các tích ở trên. 44 Ví dụ 4-4 J L J K JKL M = F(J,K,L) = J L + J K + J K L 1 0 1 1 0 0 0 1 L L J K J KJ K 0 1 2 3 6 7 4 5 J KM 23 45 Ví dụ 4-5 A C Z = F(A,B,C) = A C + B C 1 0 0 0 0 1 1 1 C C A B A B A BA B 0 1 2 3 6 7 4 5 B C 46 Ví dụ 4-6 1 1 0 1 1 1 0 0 C C A B A B A BA B A B A B A C B C F1 = F(A,B,C) = A B + A B + A C F2 = F(A,B,C) = A B + A B + B C 24 47 Ví dụ 4-7 0 1 4 5 12 13 8 9 3 2 7 6 15 14 11 10 W X W X W XW X Y Z Y Z Y Z Y Z 0 1 0 1 0 0 0 1 1 0 1 0 1 1 0 0 W X Y X Y ZW Z F1 = F(w,x,y,z) = W X Y + W Z + X Y Z 48 Ví dụ 4-8 Rút gọn biểu thức sau đây: f(A,B,C,D) = ∑(2,3,4,5,7,8,10,13,15) 11 111 11 11 AB CD 00 01 11 10 00 01 11 10 F 25 49 Ví dụ 4-8 11 111 11 11 AB CD 00 01 11 10 00 01 11 10 F BD ABC ABD ABC f(A,B,C,D) = BD + ABC + ABD + ABC 50 Trạng thái Don’t Care Một số mạch logic có đặc điểm: với một số giá trị ngõ vào xác định, giá trị ngõ ra không được xác định cụ thể. Trạng thái không xác định của ngõ ra được gọi là trạng thái Don’t Care. Với trạng thái này, giá trị của nó có thể là 0 hoặc 1. Trạng thái Don’t Care rất tiện lợi trong quá trình rút gọn bìa Karnaugh. 26 51 Ví dụ trạng thái Don’t Care 52 Ví dụ 4-9 Z 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F2 1 x 1 0 0 x 0 x x 1 0 1 x 1 1 1 Y 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 X 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 W 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 Y Z F2 = F(w,x,y,z) = X Y Z + Y Z + X Y X Y Z X Y 0 1 4 5 12 13 8 9 3 2 7 6 15 14 11 10 W X W X W XW X Y Z Y Z Y Z Y Z X X 1 1 1 1 1 0 1 0 X X 0 X 1 0 27 53 Ví dụ 4-10 Xác định biểu thức cho bảng chân trị sau đây D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 0 1 0 1 1 x 0 1 0 0 0 1 x x x x C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 Dạng chuẩn tắc tuyển f(A,B,C,D) = ∑(1,3,4,7,11) + d(5,12,13,14,15) Dạng chuẩn tắc hội f(A,B,C,D) = ∏(0,2,6,8,9,10)•D(5,12,13,14,15) 54 Ví dụ 4-10 f(A,B,C,D) = ∑(1,3,4,7,11) + d(5,12,13,14,15) f(A,B,C,D) = (0,2,6,8,9,10)•D(5,12,13,14,15) x 1x11 xx1 x1 AB CD 00 01 11 10 00 01 11 10 F 0x00 x 0xx 0x0 AB CD 00 01 11 10 00 01 11 10 F CTT CTH 28 55 Ví dụ 4-10 x 1x11 xx1 x1 AB CD 00 01 11 10 00 01 11 10 F 0x00 x 0xx 0x0 AB CD 00 01 11 10 00 01 11 10 F f(A,B,C,D) = CD + BC + AD f(A,B,C,D) = (B+D)(A+C)(C+D) 56 K-map 5 biến f(A,B,C,D,E) = ∑(0,2,4,7,10,12,13,18,23,26,28,29) BC DE 00 01 11 10 00 01 11 10 F BC DE 00 01 11 10 00 01 11 10 F A=0 A=1 0 1 3 2 4 5 7 6 12 13 15 14 8 9 11 10 16 17 19 18 20 21 23 22 28 29 31 30 24 25 27 26 29 57 K-map 5 biến f(A,B,C,D,E) = ∑(0,2,4,7,10,12,13,18,23,26,28,29) BC DE 00 01 11 10 00 01 11 10 F BC DE 00 01 11 10 00 01 11 10 F A=0 A=1 1 1 1 1 1 1 1 1 1 1 1 1 58 K-map 5 biến f(A,B,C,D,E) = ∑(0,2,4,7,10,12,13,18,23,26,28,29) 11 1 1 111 BC DE 00 01 11 10 00 01 11 10 F 11 1 1 1 BC DE 00 01 11 10 00 01 11 10 FA=0 A=1 ABDE BCD BCDE CDE f(A,B,C,D) = ABDE+BCD+BCDE+CDE 30 59 Cổng EX-OR Cổng EX-OR có hai ngõ vào. Ngõ ra của cổng EX-OR ở mức cao chỉ khi hai ngõ vào có giá trị khác nhau. 60 Cổng EX-OR 31 61 IC EX-OR 74LS86 62 Cổng EX-NOR Cổng EX-NOR có hai ngõ vào. Ngõ ra của cổng EX-NOR ở mức cao chỉ khi hai ngõ vào có giá trị giống nhau. 32 63 Cổng EX-NOR 64 Ví dụ 4-11 Sử dụng cổng EX-NOR để đơn giản mạch logic sau 33 65 Mạch tạo và kiểm tra parity 66 Mạch Enable/Disable 34 67 Đặc điểm của IC số IC được cấu tạo từ các điện trở, diode, transistor, các linh kiện này được đặt trên một lớp bán dẫn làm nền. Để tránh các tác động cơ học, hóa học, IC được đóng trong những vỏ silicon hoặc plastic. Chip thực tế nhỏ hơn hình dáng của nó rất nhiều 68 Dạng cơ bản của IC số Dạng hai hàng chân song song 35 69 Dạng cơ bản của IC số Dạng hai hàng chân song song 70 Dạng cơ bản của IC số Dạng đóng vỏ hộp (flat pack) 36 71 Đế gắn IC Để thuận lợi trong quá trình lắp ráp và thay đổi, IC thường được gắn trên các đế. 72 Mạch số tích hợp (IC) 1,000,000 or moreGiga-scale integration (GSI) 100,000 to 999,999Ultra large-scale integration (ULSI) 10,000 to 99,999Very large-scale integration (VLSI) 100 to 9999Large-scale integration (LSI) 12 to 99Medium-scale integration (MSI) <12Small-scale integration (SSI) Số cổng logicĐộ tích hợp 37 73 IC số Bipolar và Unipolar IC số được phân thành IC bipolar và IC unipolar. IC bipolar là những IC được tạo thành từ những transistor BJT (PNP hoặc NPN) IC unipolar được tạo thành từ những transistor hiệu ứng trường (MOSFET) 74 Cổng NOT bipolar và unipolar 38 75 Họ IC IC số được phân thành hai loại chính là TTL và CMOS. Họ TTL là những IC bipolar (bảng 4-1) Họ CMOS là những IC unipolar (bảng 4-2) 76 Họ TTL (Bảng 4-1) 74ALS0474ALSAdvanced low-power Schottky TTL 74AS0474ASAdvanced Schottky TTL 74LS0474LSLow-power Schottky TTL 74S0474SSchottky TTL 7404 (NOT)74Standard TTL Ví dụ ICKý hiệuPhân loại TTL 39 77 Họ CMOS (Bảng 4-2) 74ACT0274ACTAdvanced-performance CMOS, not pin but electrically compatible with TTL 74AC0274ACAdvanced-performance CMOS, not pin or electrically compatible with TTL 74HCT0274HCTSilicon-gate, high-speed, pin- compatible and electrically compatible with TTL 74HC0274HCSilicon-gate, pin-compatible with TTL, high-speed 74C0274CMetal-gate, pin-compatible with TTL 4001 (NOR)40Metal-gate CMOS Ví dụ ICKý hiệuPhân loại CMOS 78 Nguồn cung cấp và nối đất Để có thể sử dụng được những IC số ta cần phải cung cấp nguồn cho nó. Chân nguồn (power) ký hiệu là VCC cho họ TTL và VDD cho họ CMOS. Chân đất (ground) 40 79 Mức điện áp TTL Maximum 5.0 V 4.0 V 3.0 V 2.0 V 1.0 V Minimum 0.0 V Input Voltage 5.0 V Maximum 4.0 V 3.0 V 2.0 V 1.0 V 0.0 V Minimum Output Voltage Undefined Region Typical 3.5 V Typical 0.1 V Undefined Region 2.0 V HIGH HIGH 2.4 V 0.8 V LOW 0.4 V LOW 80 Mức nhiễu TTL Mức nhiễu (0.4 V) Mức nhiễu (0.4 V) Maximum 5.0 V 4.0 V 3.0 V 2.0 V 1.0 V Minimum 0.0 V Input Voltage 5.0 V Maximum 4.0 V 3.0 V 2.0 V 1.0 V 0.0 V Minimum Output Voltage Undefined Region Typical 3.5 V Typical 0.1 V Undefined Region 2.0 V HIGH HIGH 2.4 V 0.8 V LOW 0.4 V LOW 41 81 Mức điện áp CMOS Maximum 5.0 V 4.0 V 3.0 V 2.0 V 1.0 V Minimum 0.0 V Input Voltage 1.0 V LOW 3.5 V HIGH Undefined Region 5.0 V Maximum 4.0 V 3.0 V 2.0 V 1.0 V 0.0 V Minimum Output Voltage HIGH 4.9 V LOW 0.1 V Undefined Region 82 Mức nhiễu CMOS Mức nhiễu (0.9 V) Mức nhiễu (1.4 V) Maximum 5.0 V 4.0 V 3.0 V 2.0 V 1.0 V Minimum 0.0 V Input Voltage 1.0 V LOW 3.5 V HIGH Undefined Region 5.0 V Maximum 4.0 V 3.0 V 2.0 V 1.0 V 0.0 V Minimum Output Voltage HIGH 4.9 V LOW 0.1 V Undefined Region 42 83 Ngõ vào không kết nối Với họ TTL, ngõ vào không kết nối làm việc giống như mức logic 1, tuy nhiên khi đo thì điện áp DC tại chân đó nằm trong khoảng 1,4 – 1,8V. Với học CMOS tất cả các ngõ vào phải được kết nối. 84 Những lỗi bên trong IC Ngõ vào hoặc ra bị nối đến đất hoặc nguồn VCC 43 85 Những lỗi bên trong IC Ngõ vào hoặc ra bị hở mạch 86 Những lỗi bên trong IC Ngắn mạch giữa hai chân 44 87 Những lỗi bên ngoài IC Đường dây tín hiệu bị hở mạch: dây đứt, mối hàn không tốt, chân IC gãy, chân đế IC gãy. Đường dây tín hiệu bị ngắn mạch: do đường dây, mối hàn, board mạch bị đứt. Nguồn cung cấp không đúng. Output loading: khi ngõ ra kết nối với quá nhiều ngõ vào khác. 88 Câu hỏi?
File đính kèm:
 bai_giang_ky_thuat_so_chuong_4_mach_logic_dang_ngoc_khoa.pdf
bai_giang_ky_thuat_so_chuong_4_mach_logic_dang_ngoc_khoa.pdf

