Bài giảng Kỹ thuật số - Chương 3: Các cổng logic và đại số Boolean - Đặng Ngọc Khoa
Hằng số Boolean và biến
Khác với các đại số khác, các hằng và
biến trong đại số Boolean chỉ có hai giá
trị: 0 và 1
Trong đại số Boolean không có: phân số,
số âm, lũy thừa, căn số,
Đại số Boolean chỉ có 3 toán tử:
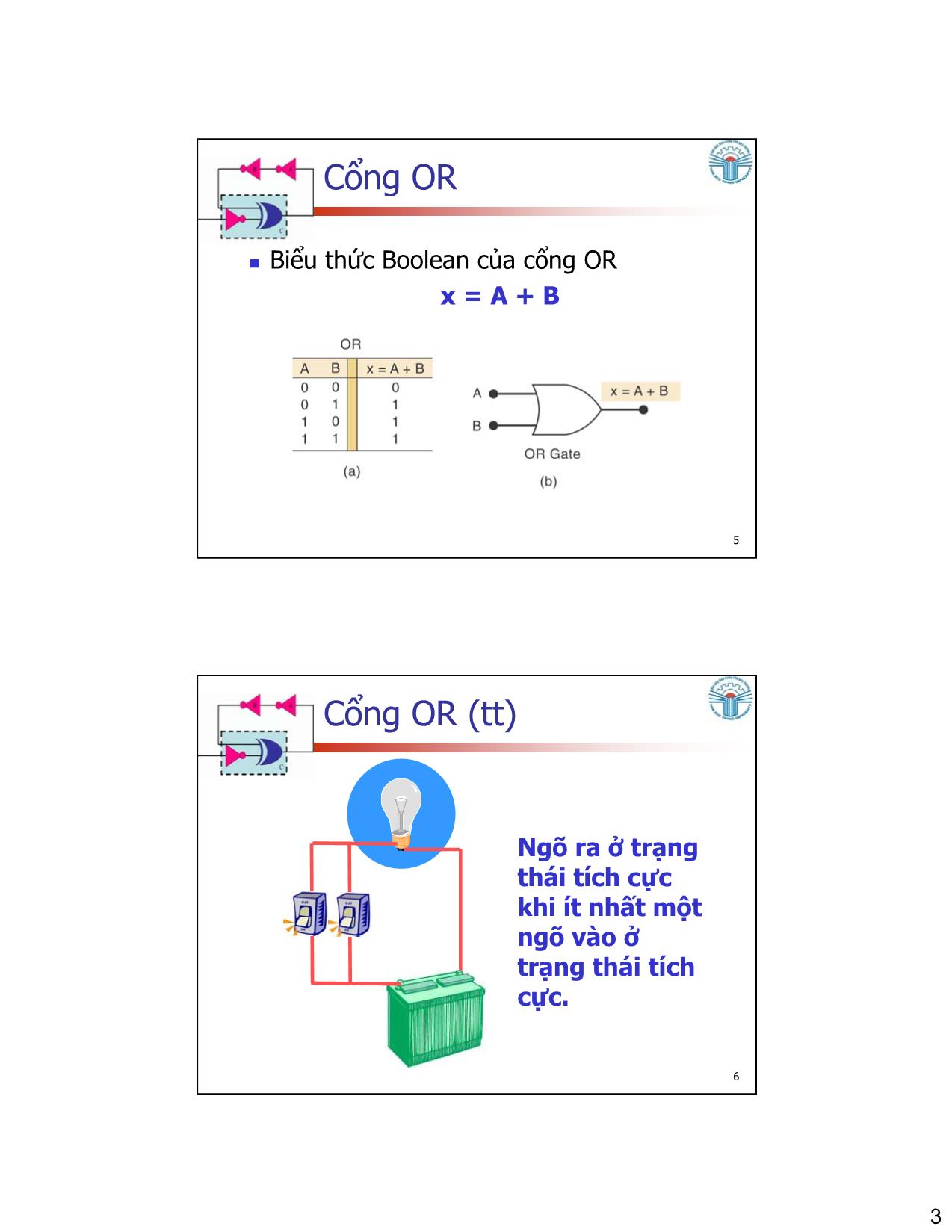
Cộng logic, hay còn gọi toán tử OR
Nhân logic, hay còn gọi toán tử AND
Bù logic, hay còn gọi toán tử NOT
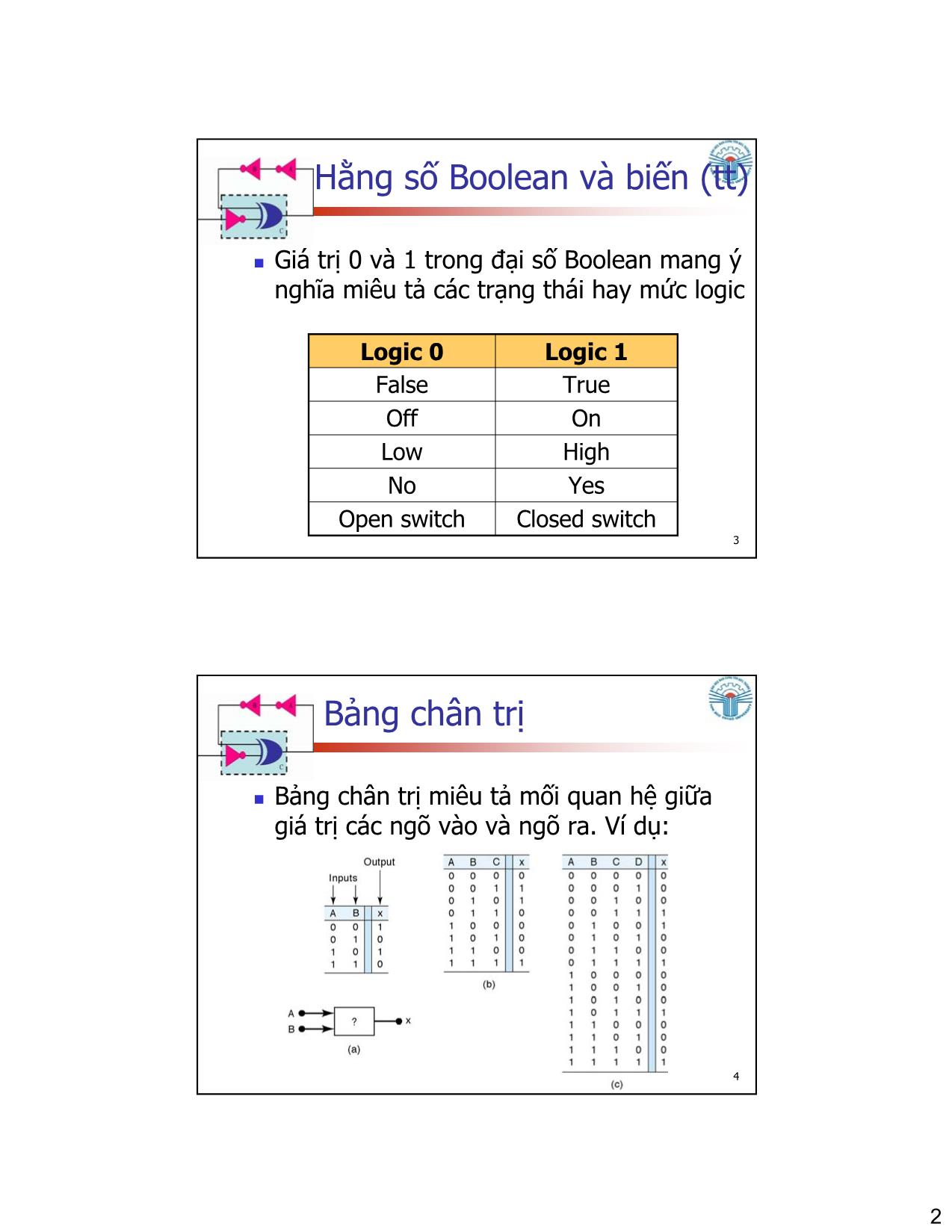
Hằng số Boolean và biến (tt)
Giá trị 0 và 1 trong đại số Boolean mang ý
nghĩa miêu tả các trạng thái hay mức logic

Trang 1
Trang 2
Trang 3
Trang 4
Trang 5
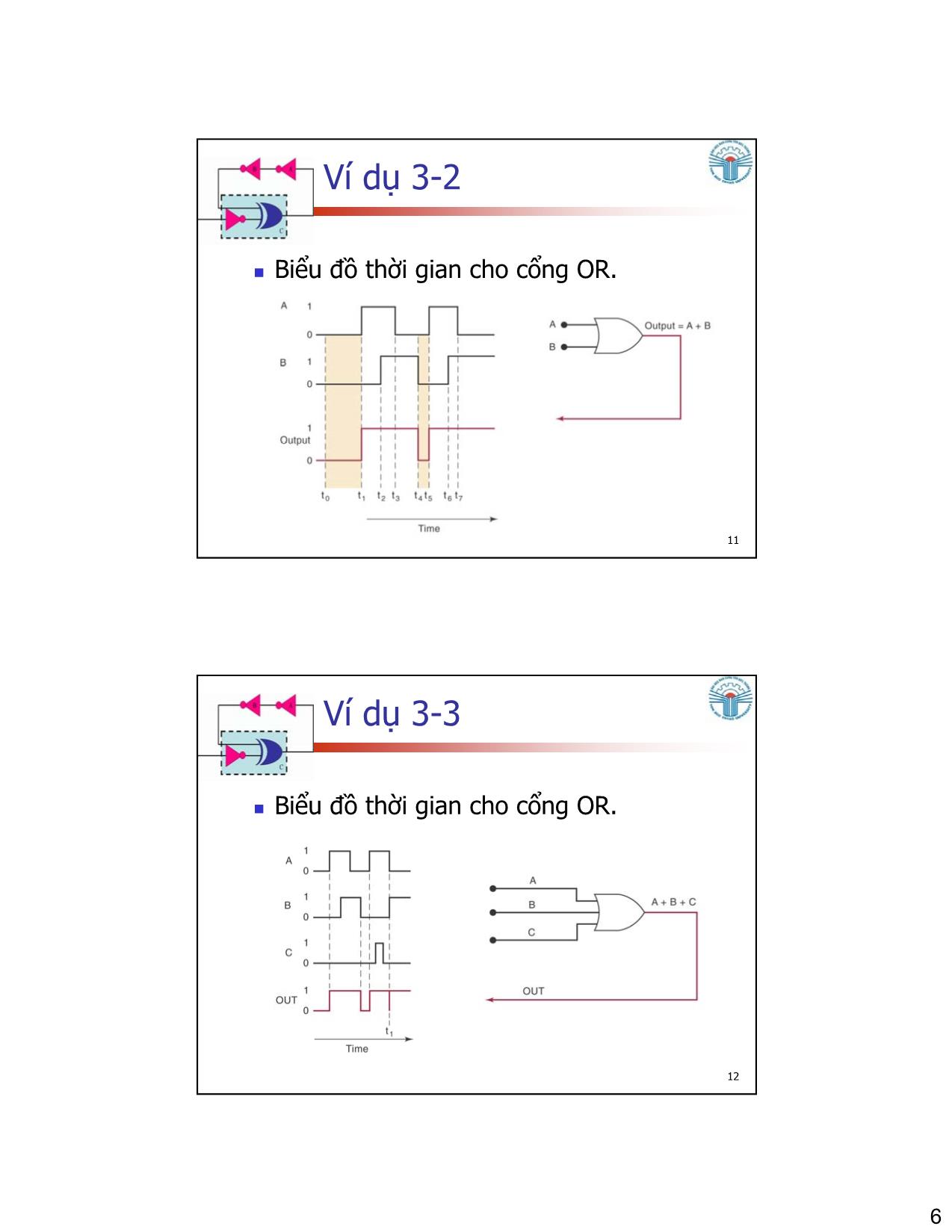
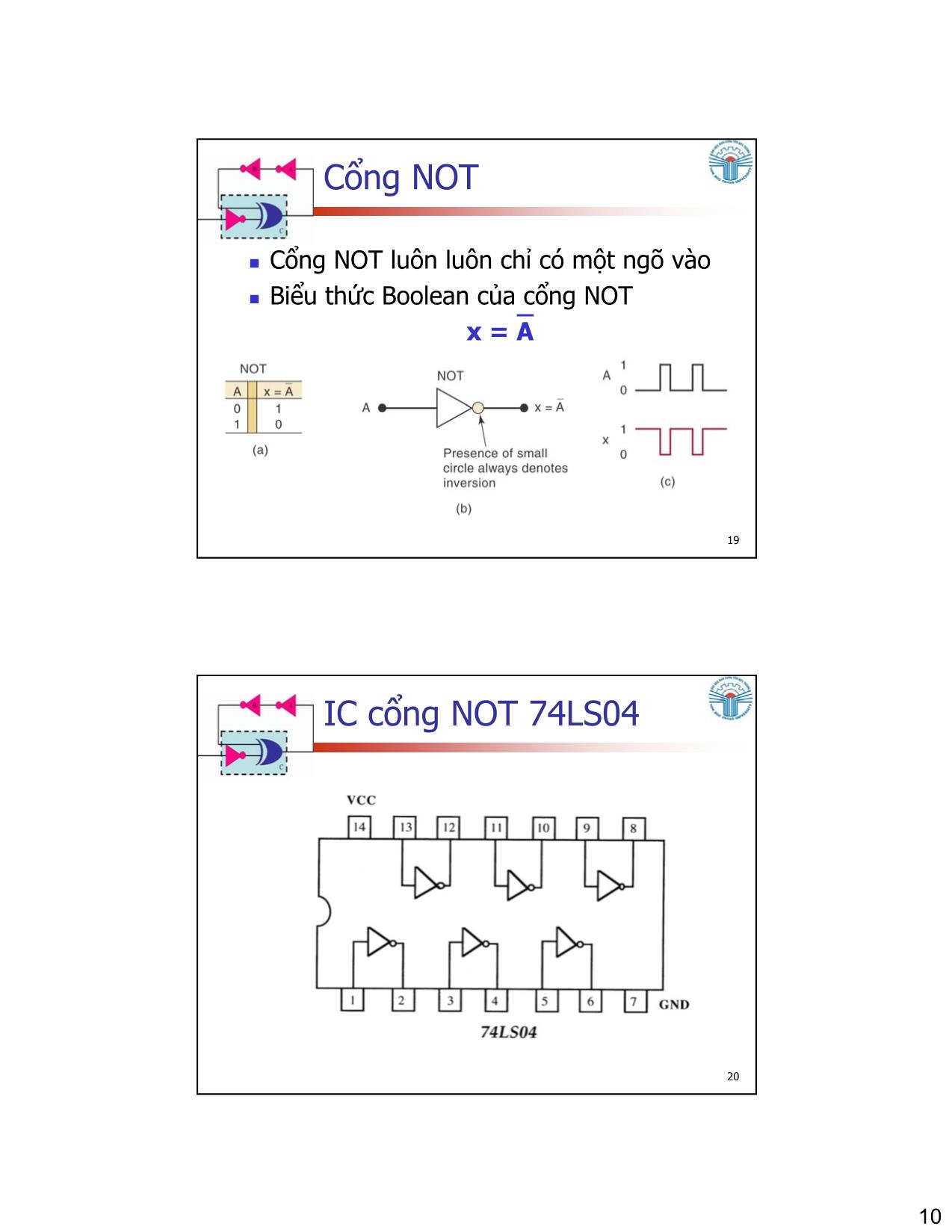
Trang 6
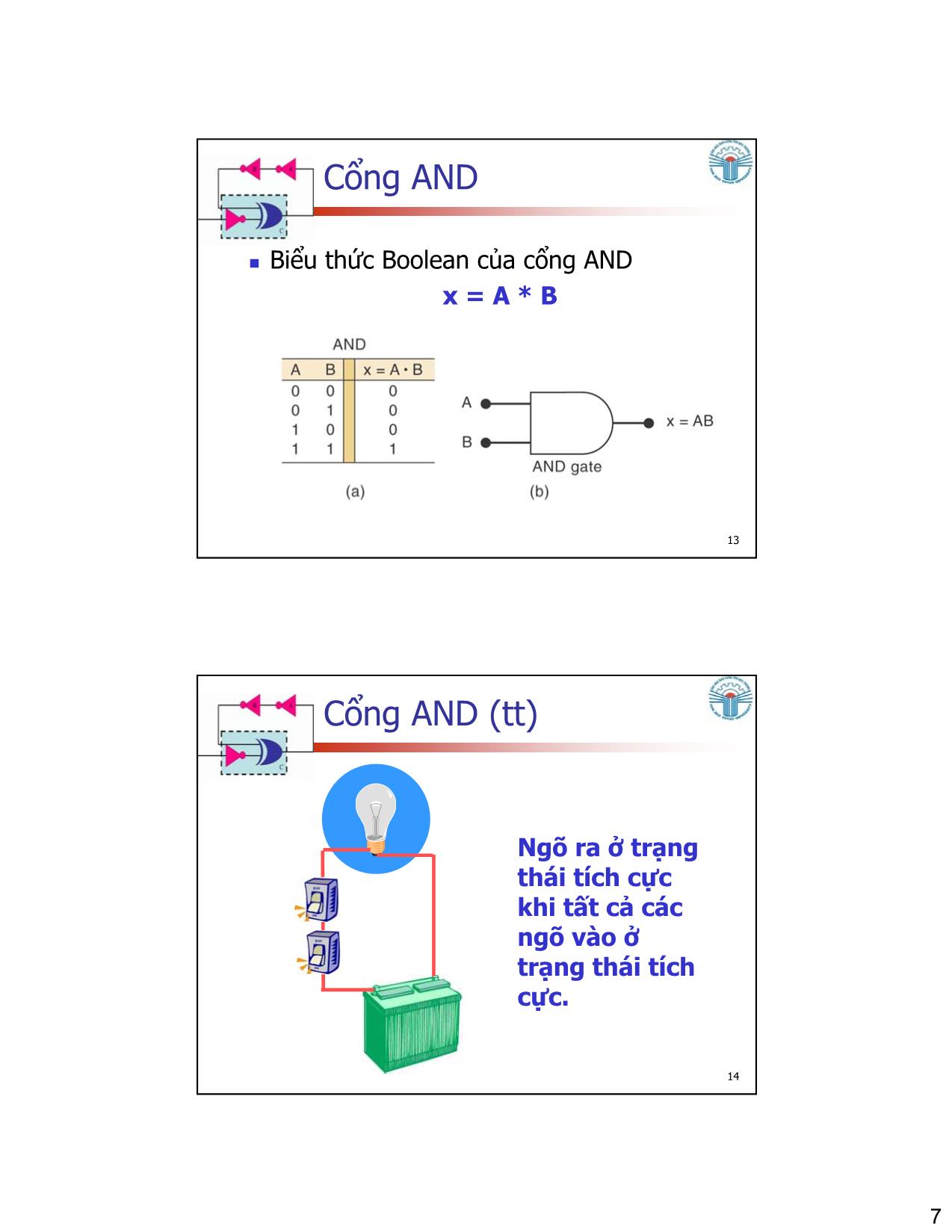
Trang 7
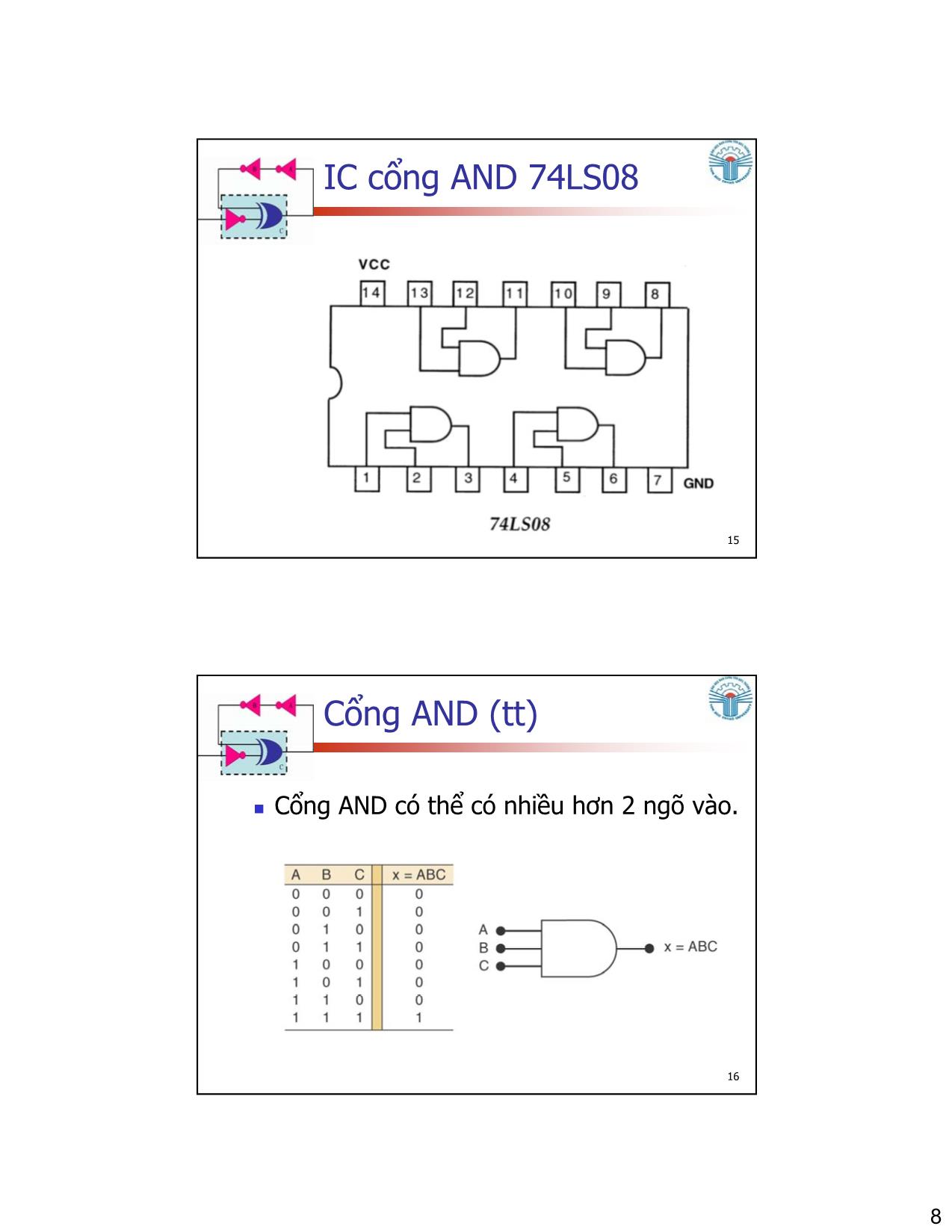
Trang 8
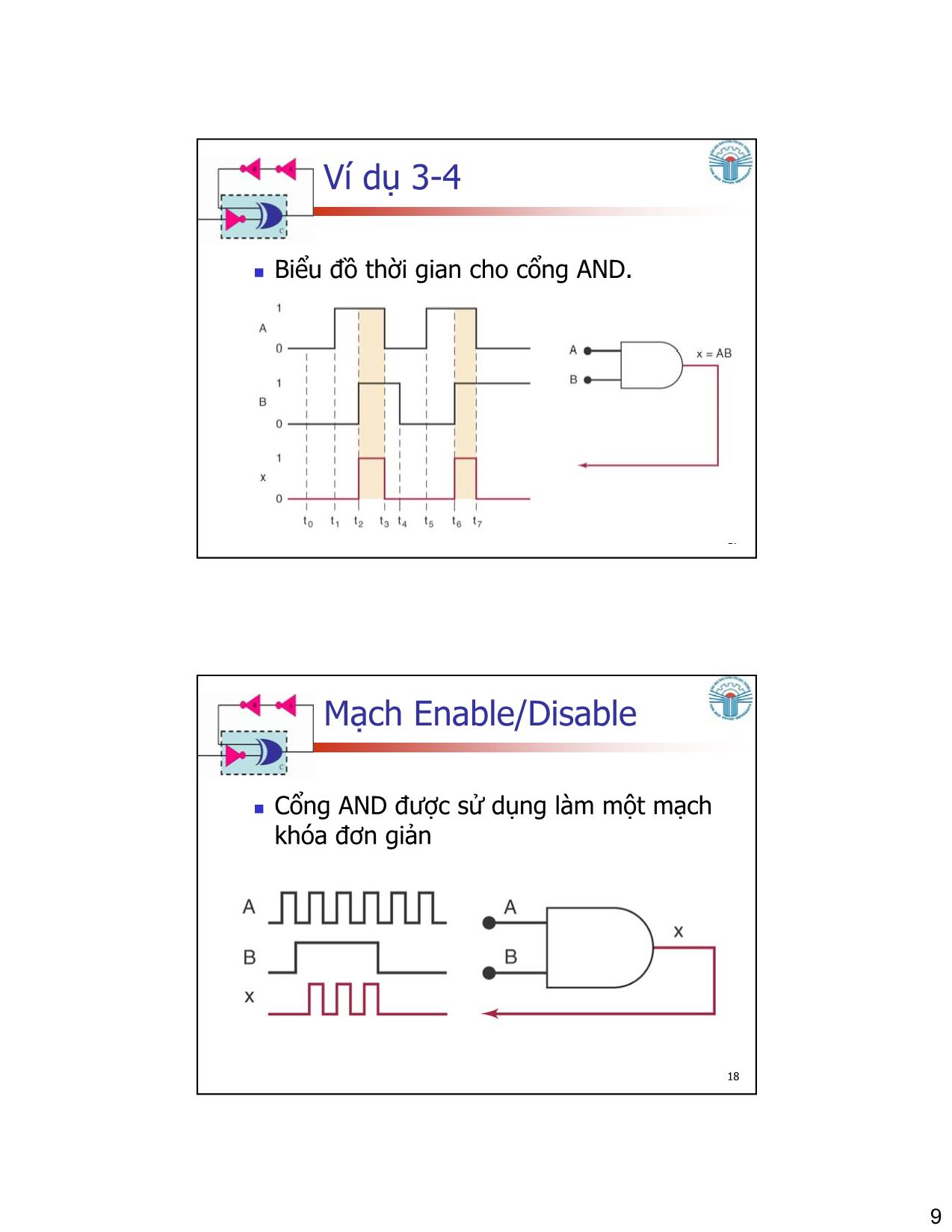
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kỹ thuật số - Chương 3: Các cổng logic và đại số Boolean - Đặng Ngọc Khoa", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật số - Chương 3: Các cổng logic và đại số Boolean - Đặng Ngọc Khoa

11 Chương 3 Các cổng logic & Đại số Boolean Th.S Đặng Ngọc Khoa Khoa Điện - Điện Tử 2 Hằng số Boolean và biến Khác với các đại số khác, các hằng và biến trong đại số Boolean chỉ có hai giá trị: 0 và 1 Trong đại số Boolean không có: phân số, số âm, lũy thừa, căn số, Đại số Boolean chỉ có 3 toán tử: Cộng logic, hay còn gọi toán tử OR Nhân logic, hay còn gọi toán tử AND Bù logic, hay còn gọi toán tử NOT 23 Closed switchOpen switch YesNo HighLow OnOff TrueFalse Logic 1Logic 0 Hằng số Boolean và biến (tt) Giá trị 0 và 1 trong đại số Boolean mang ý nghĩa miêu tả các trạng thái hay mức logic 4 Bảng chân trị Bảng chân trị miêu tả mối quan hệ giữa giá trị các ngõ vào và ngõ ra. Ví dụ: 35 Biểu thức Boolean của cổng OR x = A + B Cổng OR 6 Cổng OR (tt) Ngõ ra ở trạng thái tích cực khi ít nhất một ngõ vào ở trạng thái tích cực. 47 IC cổng OR 74LS32 8 IC cổng OR 74LS32 59 Cổng OR (tt) Cổng OR có thể có nhiều hơn 2 ngõ vào. 10 Ví dụ 3-1 Cổng OR được sử dụng trong một hệ thống báo động. 611 Ví dụ 3-2 Biểu đồ thời gian cho cổng OR. 12 Ví dụ 3-3 Biểu đồ thời gian cho cổng OR. 713 Biểu thức Boolean của cổng AND x = A * B Cổng AND 14 Cổng AND (tt) Ngõ ra ở trạng thái tích cực khi tất cả các ngõ vào ở trạng thái tích cực. 815 IC cổng AND 74LS08 16 Cổng AND (tt) Cổng AND có thể có nhiều hơn 2 ngõ vào. 917 Ví dụ 3-4 Biểu đồ thời gian cho cổng AND. 18 Mạch Enable/Disable Cổng AND được sử dụng làm một mạch khóa đơn giản 10 19 Cổng NOT luôn luôn chỉ có một ngõ vào Biểu thức Boolean của cổng NOT x = A Cổng NOT 20 IC cổng NOT 74LS04 11 21 IC cổng NOT 74LS04 22 Ngõ ra của cổng NOT xác định trạng thái của nút nhấn. Ví dụ 3-5 12 23 Miêu tả đại số mạch logic Bất kỳ mạch logic nào cũng có thể được xây dựng từ 3 cổng logic cơ bản: AND, OR và NOT. Ví dụ: x = AB + C x = (A+B)C x = (A+B) x = ABC(A+D) 24 Ví dụ 3-6 13 25 Ví dụ 3-7 26 Ví dụ 3-8 14 27 Xác định giá trị ngõ ra Cho mạch có biểu thức x = ABC(A+D) Xác định giá trị ngõ ra x khi A=0, B=1, C=1, D=1 Giá trị ngõ ra có thể được xác định 28 Thiết lập bảng chân trị Ví dụ hãy thiết lập bảng chân trị từ sơ đồ mạch logic sau đây 2INPUTS = Số trạng thái ngõ vào 23 = 8 trạng thái 111 011 101 001 110 010 100 000 xCBA 15 29 Thiết lập bảng chân trị 111 011 101 001 110 010 100 000 xCBA 0 0 0 0 1 0 0 0 1 0 1 0 0 1 1 30 Thiết lập mạch từ biểu thức Hãy thiết kế một mạch logic được xác định bởi biểu thức: y = AC + BC + ABC Khi một mạch được định nghĩa bởi biểu thức logic, ta có thể thiết kế mạch logic trực tiếp từ biểu thức đó. Biểu thức gồm 3 thành phần OR với nhau. Ngõ vào của cổng OR là ngõ ra của các cổng AND 16 31 Thiết lập mạch từ biểu thức 32 Thiết lập mạch từ biểu thức Ví dụ hãy thiết lập mạch logic cho biểu thức x = (A + B)(B + C) 17 33 Biểu thức Boolean của cổng NOR x = A + B Cổng NOR 34 IC cổng NOR 74LS02 18 35 Ví dụ 3-9 Biểu đồ thời gian cho cổng NOR. 36 Biểu thức Boolean của cổng NAND x = A * B Cổng NAND 19 37 IC cổng NAND 74LS00 38 Ví dụ 3-10 Biểu đồ thời gian cho cổng NAND. 20 39 Các định lý cơ bản trong đại số Boolean 40 Các định lý đơn biến x * 0 = 0 x * 1 = x x * x = x x * x = 0 x + 0 = x x + 1 = 1 x + x = x x + x = 1 21 41 Các định lý nhiều biến Luật giao hoán x * y = y * x x + y = y + x Luật kết hợp (x * y) * z = x * (y * z) (x + y) + z = x + (y + z) 42 Các định lý nhiều biến (tt) Luật phân phối x * (y + z) = xy + xz (x + y)(w + z) = xw + xz +yw + yz Luật hoàn nguyên x = x 22 43 Một số công thức thường dùng a) x.y + x.y = x b) x + x.y = x c) x + x.y = x + y 44 Định lý DeMORGAN Định lý DeMORGAN 2 biến x.y = x + y x + y = x.y Định lý DeMorGAN nhiều biến x.y.z.w = x + y + z + w x + y + z + = x.y.z 23 45 Áp dụng định lý DeMORGAN 46 Áp dụng định lý DeMORGAN 24 47 Sự đa nhiệm của cổng NAND 48 Sự đa nhiệm của cổng NOR 25 49 Miêu tả cổng logic 50 Miêu tả cổng logic (tt) Khi một ngõ vào hay ngõ ra trên cổng logic có ký hiệu vòng tròn thì ngõ vào hay ngõ ra đó được gọi là tích cực mức thấp. Trường hợp ngược lại, không có vòng tròn, thì gọi là tích cực mức cao. 26 51 Miêu tả cổng logic (tt) 52 Miêu tả cổng logic (tt) 27 53 Câu hỏi?
File đính kèm:
 bai_giang_ky_thuat_so_chuong_3_cac_cong_logic_va_dai_so_bool.pdf
bai_giang_ky_thuat_so_chuong_3_cac_cong_logic_va_dai_so_bool.pdf

