Bài giảng Kỹ thuật số - Chương 2: Hàm Logic
Một số định nghĩa
- Trạng thái logic là trạng thái của một thực thể. Xét về mặt
logic một thực thể chỉ tồn tại ở một trong hai trạng thái.
- Biến logic dùng đặc trưng cho trạng thái logic. Biểu diễn bởi
một ký hiệu, có giá trị là 0 hoặc 1.
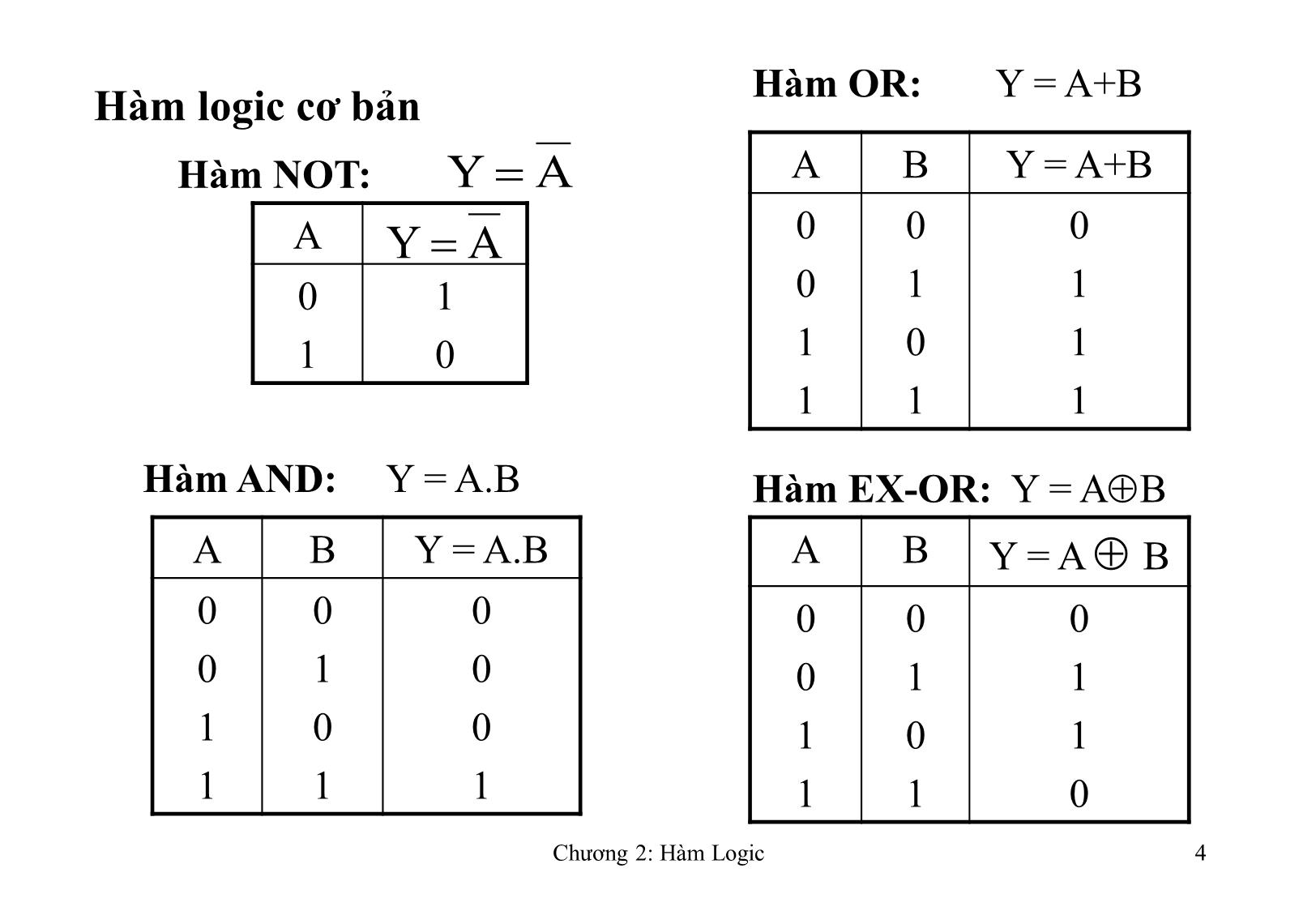
- Hàm logic diễn tả một nhóm biến logic liên hệ nhau bởi các
phép toán logic, có giá trị 0 hoặc 1 tùy theo điều kiện liên quan
đến các biến. Trong Đại số Boole chỉ có 3 toán tử:
+ Cộng logic (toán tử OR)
+ Nhân logic (toán tử AND)
+ Bù logic (toán tử NOT)
Biểu diễn biến và hàm logic
- Giản đồ Venn: Còn gọi là giản đồ Euler. Mỗi biến logic chia
không gian ra 2 vùng không gian con, một vùng giá trị biến là
đúng, vùng còn lại giá trị biến là sai.
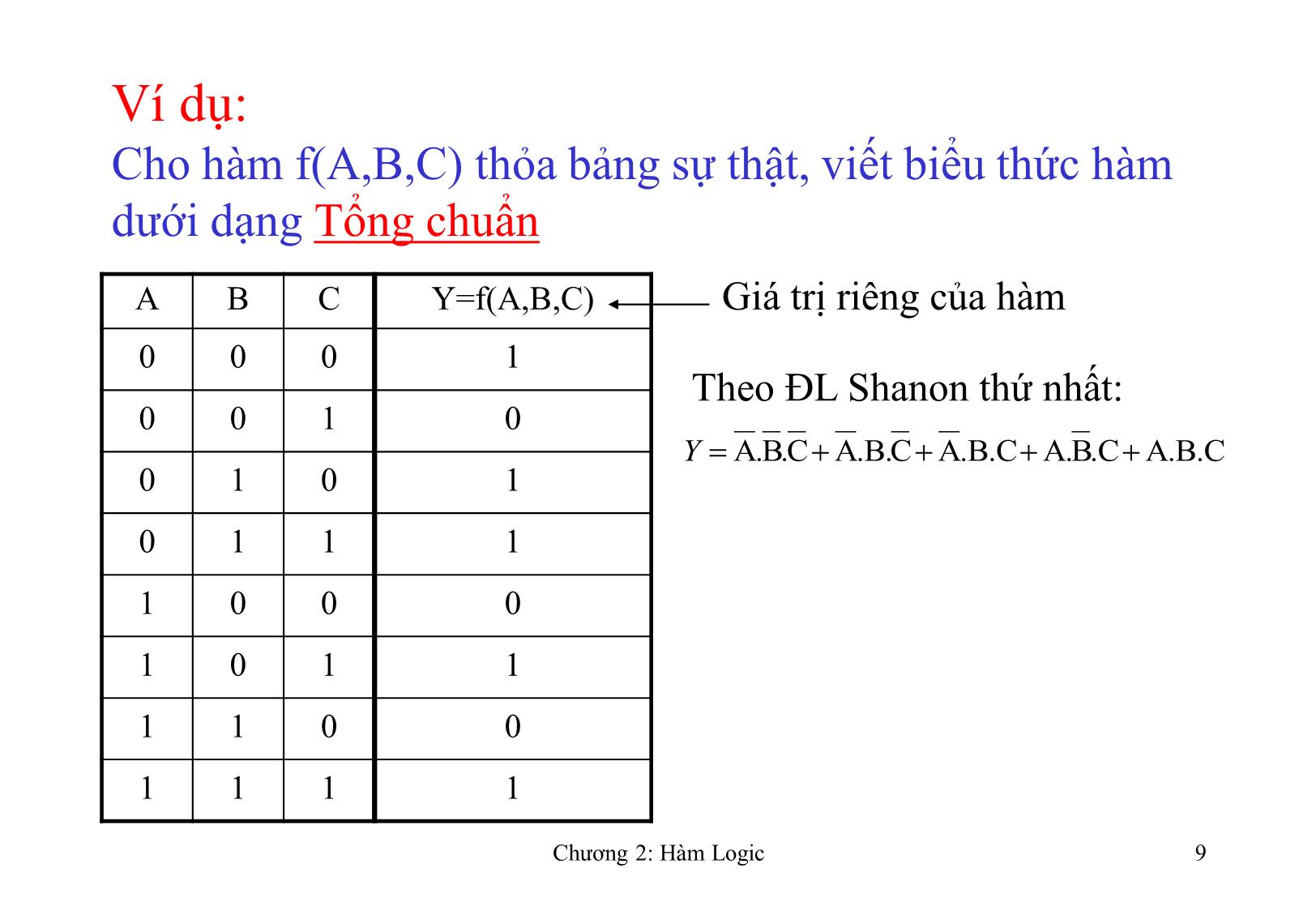
- Bảng sự thật: Nếu hàm có n biến thì bảng sự thật có n+1 cột và
2n+1 hàng. Hàng đầu: ghi tên biến và hàm, các hàng còn lại ghi các
tổ hợp có thể có của n biến (2n tổ hợp). Các cột đầu ghi giá trị của
biến, cột cuối ghi giá trị của hàm (trị riêng của hàm)
- Bảng Karnaugh: Là cách biểu diễn khác của bảng sự thật, mỗi
hàng của bảng sự thật được thay thế bởi một ô có tọa độ xác định
bởi tổ hợp của các biến. Bảng Karnaugh của n biến gồm 2n ô.
- Giản đồ thời gian: Diễn tả quan hệ giữa hàm và biến theo thời
gian, đồng thời với quan hệ logic.

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật số - Chương 2: Hàm Logic

HÀM LOGIC HÀM LOGIC CƠ BẢN CÁC DẠNG CHUẨN CỦA HÀM LOGIC RÚT GỌN HÀM LOGIC CHƢƠNG 2 Chương 2: Hàm Logic 2 HÀM LOGIC CƠ BẢN Một số định nghĩa - Trạng thái logic là trạng thái của một thực thể. Xét về mặt logic một thực thể chỉ tồn tại ở một trong hai trạng thái. - Biến logic dùng đặc trưng cho trạng thái logic. Biểu diễn bởi một ký hiệu, có giá trị là 0 hoặc 1. - Hàm logic diễn tả một nhóm biến logic liên hệ nhau bởi các phép toán logic, có giá trị 0 hoặc 1 tùy theo điều kiện liên quan đến các biến. Trong Đại số Boole chỉ có 3 toán tử: + Cộng logic (toán tử OR) + Nhân logic (toán tử AND) + Bù logic (toán tử NOT) Chương 2: Hàm Logic 3 Biểu diễn biến và hàm logic - Giản đồ Venn: Còn gọi là giản đồ Euler. Mỗi biến logic chia không gian ra 2 vùng không gian con, một vùng giá trị biến là đúng, vùng còn lại giá trị biến là sai. - Bảng sự thật: Nếu hàm có n biến thì bảng sự thật có n+1 cột và 2n+1 hàng. Hàng đầu: ghi tên biến và hàm, các hàng còn lại ghi các tổ hợp có thể có của n biến (2n tổ hợp). Các cột đầu ghi giá trị của biến, cột cuối ghi giá trị của hàm (trị riêng của hàm) - Bảng Karnaugh: Là cách biểu diễn khác của bảng sự thật, mỗi hàng của bảng sự thật được thay thế bởi một ô có tọa độ xác định bởi tổ hợp của các biến. Bảng Karnaugh của n biến gồm 2n ô. - Giản đồ thời gian: Diễn tả quan hệ giữa hàm và biến theo thời gian, đồng thời với quan hệ logic. Chương 2: Hàm Logic 4 Hàm logic cơ bản A 0 1 1 0 AY Hàm OR: Y = A+B AY Hàm NOT: A B Y = A+B 0 0 1 1 0 1 0 1 0 1 1 1 Hàm AND: Y = A.B A B Y = A.B 0 0 1 1 0 1 0 1 0 0 0 1 Hàm EX-OR: Y = AB A B Y = A B 0 0 1 1 0 1 0 1 0 1 1 0 Chương 2: Hàm Logic 5 Tính chất của các hàm logic cơ bản Tính chất cơ bản: - Có một phần tử trung tính duy nhất cho mỗi toán tử (+) và (.) A + 0 = A ; A . 1 = A - Tính giao hoán A + B = B + A ; A . B = B . A - Tính phối hợp (A + B) + C = A + (B + C) = A + B + C (A . B) . C = A . (B . C) = A . B . C - Tính phân bố Phân bố đ/v phép nhân: A . (B + C) = A . B + A . C Phân bố đ/v phép cộng: A + (B . C) = (A + B) . (A + C) Chương 2: Hàm Logic 6 - Không có phép tính lũy thừa và thừa số A + A + ... + A = A ; A . A ... A = A (1+A) = 1 ; (A.0) = 0 -Tính bù: - Tính song đối: Tất cả các biểu thức logic vẫn đúng khi thay phép (+) bởi phép toán (.) và 0 bởi 1 và ngược lại. Định lý De-Morgan: Biến đổi qua lại giữa phép cộng và phép nhân: Đảo của tổng bằng tích các đảo. Đảo của tích bằng tổng các đảo. CBACBA .. CBACBA .. 0AA.;1AA;AA Chương 2: Hàm Logic 7 CÁC DẠNG CHUẨN CỦA HÀM LOGIC -Một hàm logic được biểu diễn dưới dạng tổ hợp của những tổng (: tổng của các tích) hay tích (: tích của các tổng). - Một hàm chuẩn logic: Mỗi số hạng chứa đầy đủ các biến ở dạng nguyên hay dạng đảo. Thí dụ: Là một tổng chuẩn. Mỗi số hạng của tổng chuẩn gọi là minterm Là một tích chuẩn. Mỗi thừa số của tích chuẩn gọi là maxterm. ZYX ZXY XYZ Z)Y,f(X, )Z Y X Z).( Y Z).(X Y (X Z)Y,f(X, tongDang : ZYX ZY XZ Z)Y,f(X, tich Dang :)Z X).( Y Z).(X Y (X Z)Y,f(X, Chương 2: Hàm Logic 8 Dạng tổng chuẩn Định lý Shanon thứ nhất: Tất cả các hàm logic có thể triển khai theo một trong những biến dưới dạng tổng của hai tích như sau: f(A,B,...,Z) = A.f(1,B,...,Z) + A.f(0,B,...,Z) Khi triển khai hàm n biến ta được tổng của 2n số hạng. Mỗi số hạng là tích các biến với trị riêng của hàm. Ý nghĩa của Định lý Shanon thứ nhất: - Số số hạng của biếu thức bằng số giá trị 1 có trong trị riêng của hàm trên bảng sự thật. - Mỗi số hạng trong tổng chuẩn là tích của các biến tương ứng với tổ hợp mà hàm có trị riêng bằng 1, biến được giữ nguyên khi có giá trị 1 và đảo khi có giá trị 0. Chương 2: Hàm Logic 9 Ví dụ: Cho hàm f(A,B,C) thỏa bảng sự thật, viết biểu thức hàm dưới dạng Tổng chuẩn A B C Y=f(A,B,C) 0 0 0 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1 Giá trị riêng của hàm Theo ĐL Shanon thứ nhất: A.B.C.CBA..B.CAC.B.AC.B.A Y Chương 2: Hàm Logic 10 Dạng tích chuẩn Định lý Shanon thứ hai: Tất cả các hàm logic có thể triển khai theo một trong những biến dưới dạng tích của hai tổng như sau: f(A,B,...,Z) = [A + f(1,B,...,Z)].[A + f(0,B,...,Z)] Khi triển khai hàm n biến ta được tổng của 2n số hạng. Mỗi số hạng là tổng các biến với trị riêng của hàm. Ý nghĩa của Định lý Shanon thứ hai: - Số thừa số của biểu thức bằng số số 0 có trong trị riêng của hàm trên bảng sự thật. - Mỗi thừa số là tổng các biến tương ứng với tổ hợp mà hàm có trị riêng bằng 0. Biến giữ nguyên nếu có giá trị bằng 0 và đảo khi có giá trị bằng 1. Chương 2: Hàm Logic 11 Ví dụ: Cho hàm f(A,B,C) thỏa bảng sự thật, viết biểu thức hàm dưới dạng Tích chuẩn A B C Y=f(A,B,C) 0 0 0 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 0 1 1 1 1 Giá trị riêng của hàm Theo ĐL Shanon thứ hai: CBA.CBA.CBA Y Chương 2: Hàm Logic 12 Biến đổi qua lại giữa 2 dạng tổng chuẩn và tích chuẩn • Thêm cột trên bảng sự thật. • Viết biểu thức dưới dạng chuẩn cho • Lấy đảo 2 vế. • Dùng ĐL De-Morgan 2 lần. ),,( CBAfY Y Chương 2: Hàm Logic 13 Ví dụ: Biến đổi qua lại giữa 2 dạng tổng chuẩn và tích chuẩn A B C Y=f(A,B,C) 0 0 0 1 0 0 0 1 0 1 0 1 0 1 0 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 0 1 1 1 1 1 0 CBA.CBA.CBA Y Y Theo ĐL Shanon thứ hai: Y C)BAC).(BA).(CB(A CA.B..CB.A...CB.A CA.B.CB.A..CB.A CA.B.CB.A..CB.AY Y Y Y Viết hàm Chương 2: Hàm Logic 14 Dạng số Để đơn giản, ta biểu diễn hàm tổng chuẩn hay tích thuẩn bởi tập hợp các số dưới dấu tổng () hay dấu tích (). Mỗi tổ hợp được thay bằng số thập phân tương ứng với số nhị phân của chúng Chú ý: Cách này thì phải chỉ rõ trọng số của các biến (Qui ước bit bên trái nhất là MSB) Ví dụ: Y= (0,2,3,5,7) Ví dụ: Y= (1,4,6) A.B.C.CBA..B.CAC.B.AC.B.A Y Với A là MSB CBA.CBA.CBA Y Với A là MSB Chương 2: Hàm Logic 15 RÚT GỌN HÀM LOGIC Phƣơng pháp đại số (Dựa trên khả năng và kinh nghiệm mỗi ngƣời) Các đẳng thức thường dùng: AB + AB = B (A + B).(A + B) = B A + AB = A A.(A + B) = A A + AB = A + B A.(A + B) = A.B - Qui tắc 1: Sử dụng các đẳng thức trên - Qui tắc 2: Thêm một số hạng đã có trong biểu thức - Qui tắc 3: Bỏ số hạng chứa các biến đã có trong số hạng khác - Qui tắc 4: Dùng hàm chuẩn tương đương Chương 2: Hàm Logic 16 Ví dụ Rút gọn hàm bằng PP đại số ACAB 1)(BCAC)AB(1 CACABABCABY ABC ABC0.B ABCBAA C)AAB(Y A.B.CA.BC.A .ABC.A ABCA Y VD1: VD2: VD3: VD4: CB. 1)AA(CB. 0CB.CA.B.0C.B.A0 CB.C.CB.B.CA.B.C.C.AC.B.AC.A.A CC).BB).(AA(Y Chương 2: Hàm Logic 17 Phƣơng pháp: Dùng bảng Karnaugh Phương pháp bảng Karnaugh dựa vào việc nhóm các tổ hợp kề nhau trên bảng để đơn giản các biến có giá trị khác nhau trong các tổ hợp. VD: Hai tổ hợp: Khác nhau 1 bit gọi là hai tổ hợp kề nhau VD: Biến B được đơn giản Các bƣớc rút gọn hàm: - Vẽ bảng Karnaugh theo số biến của hàm - Chuyển hàm cần đơn giản vào bảng Karnaugh - Gom các ô chứa các tổ hợp kề nhau lại thành nhóm - Viết kết quả hàm rút gọn Kết quả: Hàm đƣợc rút gọn dƣới dạng tổng của các tích ABAAB BA.;A.B Chương 2: Hàm Logic 18 Chuyển hàm vào bảng Karnaugh • Mỗi ô ta đưa vào giá trị của hàm tương ứng với tổ hợp biến: chỉ ghi giá trị 1, bỏ qua giá trị 0 • Các dạng của hàm cần rút gọn: - Hàm có dạng tổng chuẩn: Đưa trực tiếp - Hàm chưa có dạng tổng chuẩn: Cần đưa về dạng tổng chuẩn (thêm vào các số hạng sao cho hàm không thay đổi nhưng các số hạng chứa đầy đủ các biến). - Hàm có dạng số thứ nhất: Ghi các số 1 vào các ô tương ứng với những số có trong hàm - Hàm có dạng tích chuẩn: Lấy hàm đảo, dùng ĐL De-Morgan đưoa về dạng tổng chuẩn, ghi các số 0 vào ô tương ứng với tổ hợp biến trong tổng chuẩn Các còn lại ghi giá trị 1. - Hàm có dạng số thứ hai: Ghi số 0 tương ứng với những số của hàm đã cho Các còn lại ghi giá trị 1. - Từ bảng sự thật: Các ô có giá trị 1 khi hàm có trị riêng là 1 - Chú ý: trường hợp hàm không xác định thì ghi chữ X vào ô tương ứng với tổ hợp biến. Chương 2: Hàm Logic 19 Qui tắc rút gọn • Gom các số 1 kế nhau thành từng nhóm sao cho số nhóm càng ít càng tốt (số số hạng trong kết quả càng ít). • Số số 1 nằm trong mỗi nhóm càng nhiều càng tốt nhưng phải là 2k. (là: 1, 2, 4, 8, 16, 32) • Không có số 1 nào chưa được gom nhóm, một số 1 có thể nằm ở nhiều nhóm khác nhau. • Các ô chưa chữ X: cho tùy ý là 0 hoặc 1 sao cho việc gom nhóm là tiện nhất. • Kết quả cuối cùng: có dạng tổng của các tích Chương 2: Hàm Logic 20 Ví dụ Dùng Bảng Karnaugh rút gọn hàm (A: MSB) ABCCBABCACBAC)B,f(A, BC A 00 01 11 10 0 1 1 1 1 1 f(A,B,C) BCCBC)B,f(A, ABCBCACBAC)B,f(A, BC A 00 01 11 10 0 1 1 1 1 f(A,B,C) BCCAC)B,f(A, Chương 2: Hàm Logic 21 Ví dụ Dùng Bảng Karnaugh rút gọn hàm (A: MSB) ABCCABCBABCAC)B,f(A, BC A 00 01 11 10 0 1 1 1 1 1 f(A,B,C) BCABACC)B,f(A, CBACBABCACBAC)B,f(A, BC A 00 01 11 10 0 1 1 1 1 1 f(A,B,C) BABABAC)B,f(A, Chương 2: Hàm Logic 22 Ví dụ Dùng Bảng Karnaugh rút gọn hàm (A: MSB) 14,15),10,11,13,(0,1,2,3,9D)C,B,f(A, CD AB 00 01 11 10 00 1 1 1 1 01 11 1 1 1 10 1 1 1 f(A,B,C,D) ACADBAD)C,B,f(A, CD AB 00 01 11 10 00 1 1 1 1 01 1 1 11 1 10 1 1 1 f(A,B,C,D) DBCBBADADABCD)C,B,f(A, 14),7,8,9,11,(0,1,2,3,5D)C,B,f(A, Chương 2: Hàm Logic 23 Ví dụ Dùng Bảng Karnaugh rút gọn hàm (A: MSB) 15)(1,3,7,11,D)C,B,f(A, CD AB 00 01 11 10 00 x 1 1 x 01 X 1 11 1 1 10 f(A,B,C,D) BDBAD)C,B,f(A, CD AB 00 01 11 10 00 1 X X 01 1 1 1 11 1 1 X 1 10 X 1 f(A,B,C,D) DBACDABDBD)C,B,f(A, (0,5,9,10)D)C,B,f(A, Các tổ hợp (0,2,5) hàm không xác định Các tổ hợp (2,3,8,15) cho hàm không xác định Chương 2: Hàm Logic 24 Ví dụ: Dùng Bảng Karnaugh rút gọn hàm (A: MSB) )6,27,29,3120,24,25,2,10,11,16,(0,5,6,8,9E)D,C,B,f(A, DE BC 00 01 11 10 00 1 01 1 1 11 10 1 1 1 1 f(B,C,D,E) ECDBAEDCBAEDBAABEEDCCBE)D,C,B,f(A, Note: Có 15 số. Từ 0 15 ở Bảng Từ 16 31 ở Bảng A A A DE BC 00 01 11 10 00 1 01 1 11 1 1 10 1 1 1 1 f(B,C,D,E) A Chương 2: Hàm Logic 25 Ví dụ: Dùng Bảng Karnaugh rút gọn hàm (A: MSB) 31),27,28,29,8,22,24,2512,13,15,1(2,7,9,11,E)D,C,B,f(A, DE BC 00 01 11 10 00 1 01 1 11 1 1 1 10 1 1 f(B,C,D,E) EDBADABEDCBCDEADBCBEE)D,C,B,f(A, Note: Có 15 số. Từ 0 15 ở Bảng Từ 16 31 ở Bảng A A A DE BC 00 01 11 10 00 1 01 1 11 1 1 1 10 1 1 1 f(B,C,D,E) A Chương 2: Hàm Logic 26 Phƣơng pháp: Quine – Mc. Cluskey Phƣơng pháp: Quine – Mc. Cluskey dựa trên tính kề nhau của các tổ hợp biến để đơn giản hàm có dạng tổng. Trong quá trình đơn giản có khả năng xuất hiện các số hạng giống nhau ta có thể bỏ bớt đi một số hạng). PP này chia làm 2 giai đoạn: Gđ1: Dựa trên tính kề của các tổ hợp biến để đơn giản số biến trong các số hạng. - Nhóm các số hạng theo số số 1 có trong tổ hợp và ghi lại theo thứ tự số 1 tăng dần. - Mỗi tổ hợp trong một nhóm sẽ so sánh với tổ hợp khác trong nhóm kế cận (ta có thể thực hiện phép trừ, nếu kết quả phép trừ là 2k thì so sánh được, và biến được đơn giản là biến có trọng số 2k, việc so sánh cho đến khi chỉ còn một nhóm.). Viết kết quả. Gđ2: Kiểm tra và thực hiện việc tối giản. Gđ2 chỉ thực hiện khi Gđ1 chưa thật sự tối giản. Chương 2: Hàm Logic 27 Ví dụ: 1 Dùng PP Quine – Mc. Cluskey rút gọn hàm (A: MSB) )(5,7,13,15D)C,B,f(A, N A B C D 5 0 1 0 1 7 0 1 1 1 13 1 1 0 1 15 1 1 1 1 Lập bảng 2 N A B C D 7-5=21 5,7 0 1 - 1 13-5=23 5,13 - 1 0 1 15-7=23 7,15 - 1 1 1 15-13=21 13,15 1 1 - 1 Lập bảng 3 N A B C D 5,7 ; 13,15 - 1 - 1 5,13 ; 7,15 - 1 - 1 Loại tổ hợp dưới do trùng với tổ hợp trên Kết quả: f(A,B,C,D) = BD GĐ1: Lập bảng 1 Chương 2: Hàm Logic 28 Ví dụ 2: Dùng PP Quine – Mc. Cluskey rút gọn hàm (A: MSB) 14),10,12,13,(1,2,4,5,6D)C,B,f(A, N A B C D 1 0 0 0 1 2 0 0 1 0 4 0 1 0 0 5 0 1 0 1 6 0 1 1 0 10 1 0 1 0 12 1 1 0 0 13 1 1 0 1 14 1 1 1 0 Lập bảng 2 N A B C D 5-1=22 1,5 0 - 0 1 6-2=22 2,6 0 - 1 0 10-2=23 2,10 - 0 1 0 5-4=20 4,5 0 1 0 - 6-4=21 4,6 0 1 - 0 12-4=23 4,12 - 1 0 0 13-5=23 5,13 - 1 0 1 14-6=23 6,14 - 1 1 0 14-10=22 10,14 1 - 1 0 13-12=20 12,13 1 1 0 - 14-12=21 12,14 1 1 - 0 Lập bảng 3 N A B C D 2,6 ; 10,14 - - 1 0 2,10 ; 6,14 - - 1 0 4,5 ; 12,13 - 1 0 - 4,6 ; 12,14 - 1 - 0 4,12 ; 5,13 - 1 0 - 4,12 ; 6,14 - 1 - 0 Loại 3 tổ hợp màu xanh do trùng với tổ hợp trên GĐ1: Lập bảng 1 DBCBDCDCAD)C,B,f(A, Chương 2: Hàm Logic 29 Ví dụ 2 (tt): Dùng PP Quine – Mc. Cluskey rút gọn hàm (A: MSB) DBCBDCDCAD)C,B,f(A, Tổ hợp (1,5) (2,6 ; 10,14) (4,5 ; 12,13) (4,6 ; 12,14) Các tổ hợp trên còn chứa các số hạng giống nhau (4, 12) KQ chưa tối giản Giai đoạn 2 GĐ2: Lập bảng Tổ hợp ở gđ1 Giá trị thập phân có trong hàm đã cho 1 2 4 5 6 10 12 13 14 1,5 * * 2,6 ; 10,14 * * * * 4,5 ; 12,13 * * * * 4,6 ; 12,14 * * * * X X X X X X X X X Xét các cột chỉ chứa 1 dấu * Các tổ hợp tương ứng với hàng đó được chọn CBDCDCAD)C,B,f(A, :KQ Chương 2: Hàm Logic 30 Ví dụ 3: Dùng PP Quine – Mc. Cluskey rút gọn hàm (A: MSB) ,11,12,15)(3,4,6,7,8D)C,B,f(A, N A B C D 4 0 1 0 0 8 1 0 0 0 3 0 0 1 1 6 0 1 1 0 12 1 1 0 0 7 0 1 1 1 11 1 0 1 1 15 1 1 1 1 Lập bảng 2 N A B C D 6-4=21 4,6 0 1 - 0 12-4=23 4,12 - 1 0 0 12-8=22 8,12 1 - 0 0 7-3=22 3,7 0 - 1 1 11-3=23 3,11 - 0 1 1 7-6=20 6,7 0 1 1 - 15-7=23 7,15 - 1 1 1 15-11=22 11,15 1 - 1 1 Lập bảng 3 N A B C D 3,7 ; 11,15 - - 1 1 3,11 ; 7,15 - - 1 1 Loại tổ hợp màu xanh do trùng với tổ hợp trên GĐ1: Lập bảng 1 CDBCADCADCBDBA D)C,B,f(A, Còn lại các tổ hợp (4,6); (4,12); (8,12) ; (6,7) ; (3,7;11,15) Chương 2: Hàm Logic 31 Ví dụ 3 (tt): Dùng PP Quine – Mc. Cluskey rút gọn hàm (A: MSB) Tổ hợp ở gđ1 Giá trị thập phân có trong hàm đã cho 3 4 6 7 8 11 12 15 4,6 * (chọn) * * 4,12 * * 8,12 * * 6,7 * * 3,7 ; 11,15 * * * * X X X X X X Các tổ hợp trên còn chứa các số hạng giống nhau (4, 6,12, 7) KQ chưa tối giản Giai đoạn 2 GĐ2: Lập bảng Còn 2 cột 4 và 6 chưa có chữ X; Trong 3 tổ hợp còn lại ta quyết định chọn tổ hợp (4;6) vì chứa đủ cả số 4 và số 6 CDDCADBAD)C,B,f(A, :KQ CDBCADCADCBDBA D)C,B,f(A, Còn lại các tổ hợp (4,6); (4,12); (8,12) ; (6,7) ; (3,7;11,15)
File đính kèm:
 bai_giang_ky_thuat_so_chuong_2_ham_logic.pdf
bai_giang_ky_thuat_so_chuong_2_ham_logic.pdf

