Bài giảng Kỹ thuật điện tử - Chương 7: Các mạch số cơ bản - Lê Chí Thông

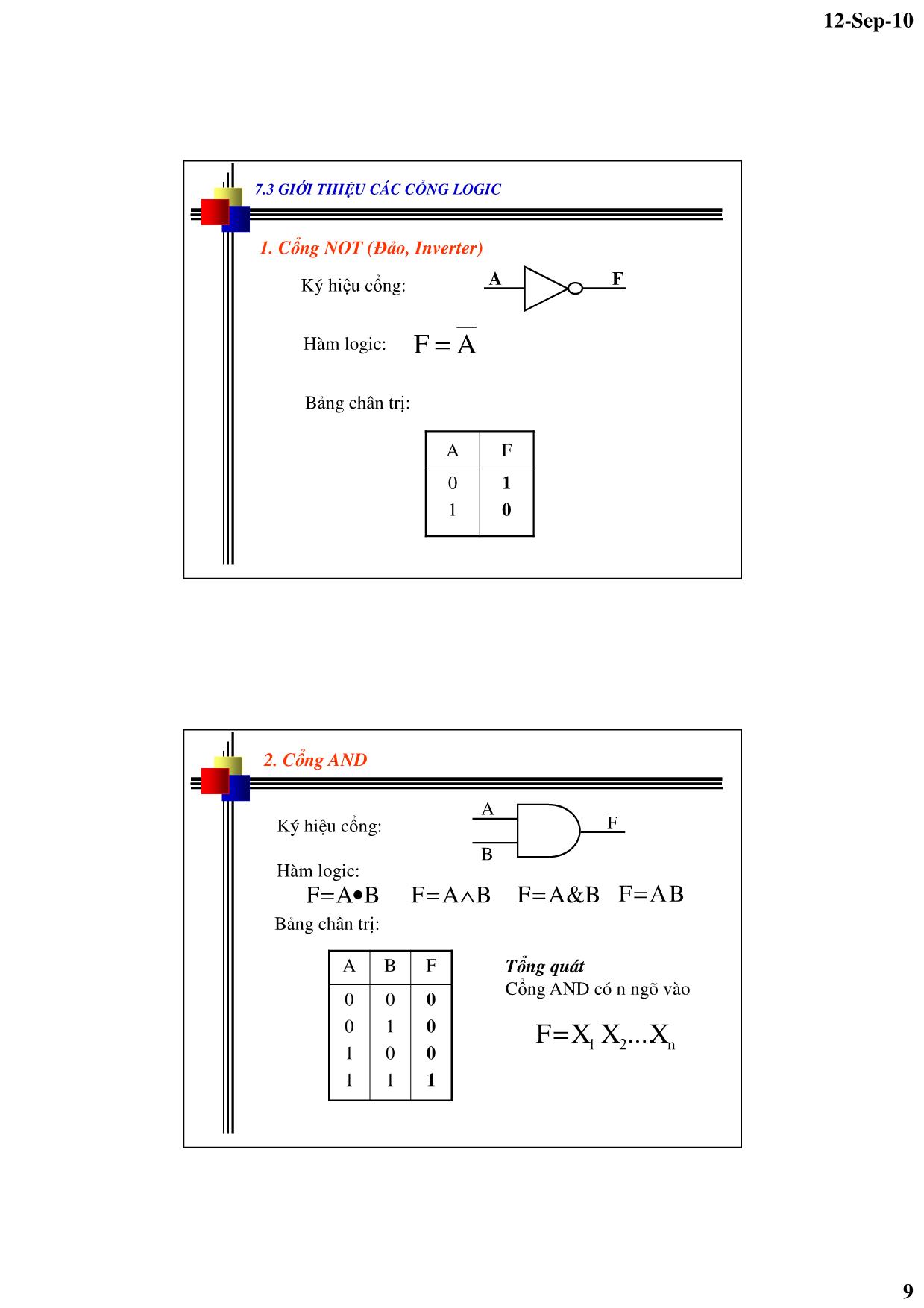
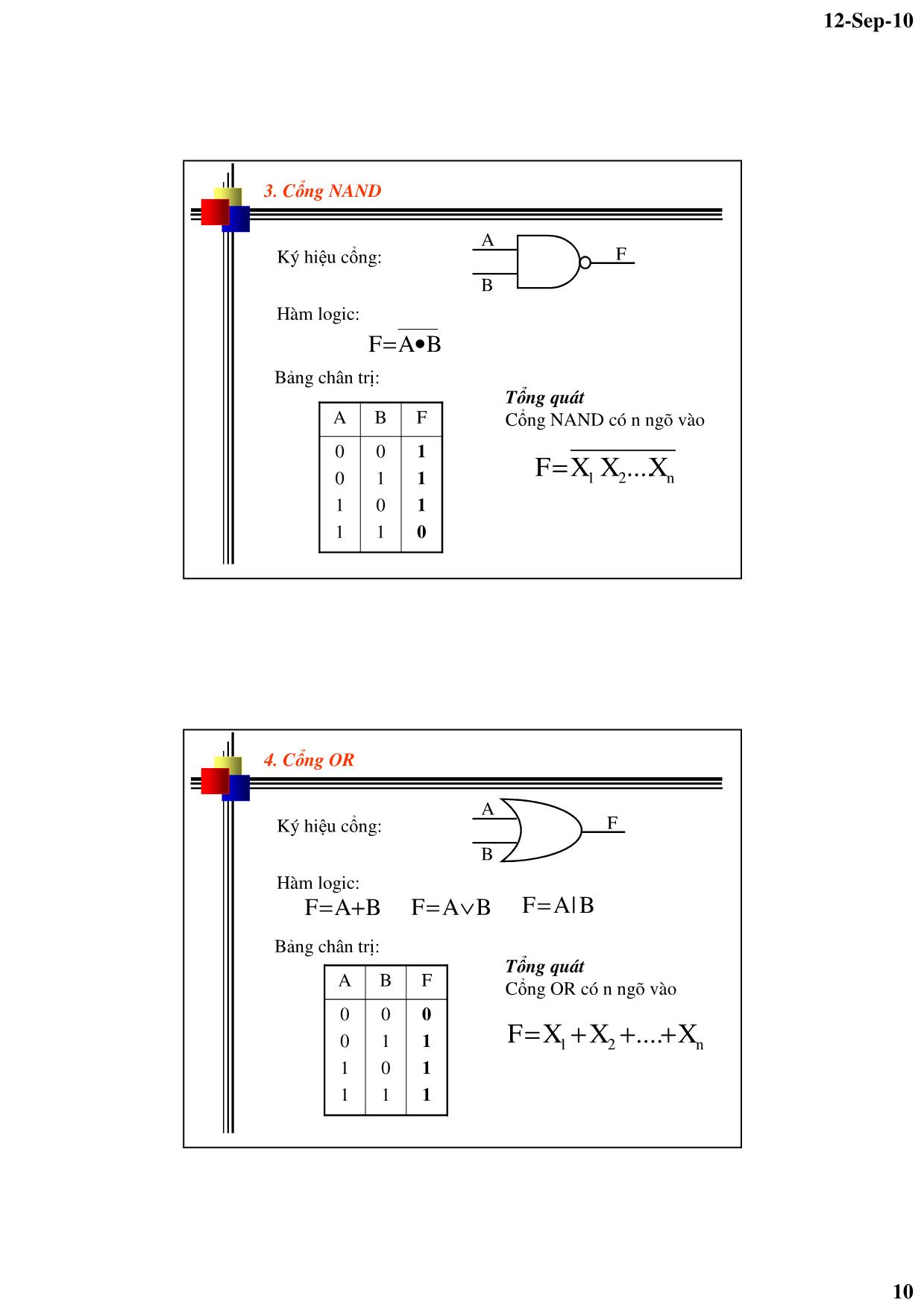
 từ trên xuống.
Trong đó:
- r là cơ số.
- Ci: ký số tại vị trí thứ i.
CÁC HỆ THỐNG SỐ KHÁC
- Hệ thống số bát phân (Octal – ký hiệu: O hay 8)
- Cơ số là 8. 
- Biểu diễn bởi 8 ký số: 0,1,2,3,4,5,6,7.
- Mỗi ký số bát phân được biểu diễn bởi 3 bit nhị phân.
- Hệ thống số thập lục phân (HexaDecimal – ký hiệu: H hay 16)
- Cơ số là 16. 
- Biểu diễn bởi 16 ký số: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
- Mỗi ký số bát phân được biểu diễn bởi 4 bit nhị phân.
12-Sep-10
6
7.2 CƠ SỞ ĐẠI SỐ BOOLE
- Đại số Boole là đại số dùng để mô tả các hoạt động logic.
- Các biến Boole là các biến logic, chỉ mang giá trị 0 hoặc 1 (đôi khi
gọi là True hoặc False).
- Hàm Boolean là hàm của các biến Boole, chỉ mang giá trị 0 hoặc 1.
- Đại số Boole gồm các phép toán cơ bản: Đảo (NOT), Giao hay 
Nhân (AND), Hợp hay Cộng (OR).
1. Giao hoán
A + B = B + A
A.B = B.A
2. Phối hợp
A + (B + C) = (A + B) + C
A.(B.C) = (A.B).C
3. Phân bố
A.(B + C) = A.B + A.C
A + (B.C) = (A + B)( A + C)
4. ∃ hai phần tử trung hòa được ký hiệu là 0 và 1
A + 0 = A
A.1= A
5. ∀A∈X, ∃ phần tử bù của A, được ký hiệu là : 
Các tiên đề của đại số Boole
A
A
A + 
= 0A .
= 1
A
12-Sep-10
7
 CÁC ĐỊNH LÝ
Định lý đối ngẫu
Một mệnh đề được gọi là đối ngẫu với một mệnh đề khác khi ta thay thế:
0 ↔ 1; (+) ↔ (.)
Phát biểu định lý: khi một mệnh đề đúng thì mệnh đề đối ngẫu của nó cũng
đúng.
Định lý DeMorgan
Phát biểu định lý: 
........ BABA =++
........ ++= BABABù của một tích bằng tổng các bù:
Bù của một tổng bằng tích các bù:
Định lý 3: (luật phủ định của phủ định)
AA =
Định lý 4:
A + 1 = 1
A . 0 = 0
Tổng quát:
A + B + C + ..+ 1 = 1
A . B . C .  . 0 = 0
CÁC ĐỊNH LÝ
12-Sep-10
8
 CÁC ĐỊNH LÝ
Định lý 5: (luật đồng nhất)
A + A = A
A . A = A
Tổng quát:
A + A + A +  + A = A
A . A . A . . . A = A 
Định lý 6: (luật hấp thu hay luật nuốt)
A + ( A . B) = A
A . (A + B) = A
Định lý 7: (luật dán)
BAB.AA
BA)BA(.A
+=+
=+
VÍ DỤ ÁP DỤNG
Chứng minh rằng:
BAAC)CA)(BA( +=++
Giải
)CA)(BA(VT ++=
BAAC +=
BCBAACAA +++=
BCBAAC ++=
)AA(BCBAAC +++=
BCAABCBAAC +++=
)BCABA()ABCAC( +++=
(đpcm)
12-Sep-10
9
7.3 GIỚI THIỆU CÁC CỔNG LOGIC 
1. Cổng NOT (Đảo, Inverter)
Ký hiệu cổng:
Hàm logic: AF =
A F
Bảng chân trị:
A F
0
1
1
0
2. Cổng AND
Ký hiệu cổng:
Hàm logic:
Bảng chân trị:
A
B
F
BAF •= BAF ∧= B&AF= BAF=
A B F
0
0
1
1
0
1
0
1
0
0
0
1
Tổng quát
Cổng AND có n ngõ vào
n21 X....XXF=
12-Sep-10
10
3. Cổng NAND
Ký hiệu cổng:
Hàm logic:
Bảng chân trị:
BAF •=
A B F
0
0
1
1
0
1
0
1
1
1
1
0
A
B
F
Tổng quát
Cổng NAND có n ngõ vào
n21 X....XXF=
4. Cổng OR
Ký hiệu cổng:
Hàm logic:
Bảng chân trị:
A B F
0
0
1
1
0
1
0
1
0
1
1
1
A
B
F
BAF += BAF ∨= B|AF=
Tổng quát
Cổng OR có n ngõ vào
n21 X....XXF +++=
12-Sep-10
11
5. Cổng NOR
Ký hiệu cổng:
Hàm logic:
Bảng chân trị:
A B F
0
0
1
1
0
1
0
1
1
0
0
0
BAF +=
A
B
F
Tổng quát
Cổng NOR có n ngõ vào
n21 X....XXF +++=
6. Cổng EXOR (XOR – Exclusive OR)
Ký hiệu cổng:
Hàm logic:
Bảng chân trị:
A B F
0
0
1
1
0
1
0
1
0
1
1
0
BABABAF +=⊕=
A
B
F
Lưu ý
Cổng XOR chỉ có 2 ngõ vào
12-Sep-10
12
7. Cổng EXNOR (XNOR – Exclusive NOR)
Ký hiệu cổng:
Hàm logic:
Bảng chân trị:
A B F
0
0
1
1
0
1
0
1
1
0
0
1
BABABAF +=⊕=
A
B
F
7.4 CÁC PHƯƠNG PHÁP BIỂU DIỄN HÀM BOOLE
1. Phương pháp đại số
Hàm Boole được biểu diễn dưới dạng một biểu thức đại số của các biến 
boole (biến nhị phân), quan hệ với nhau bởi các phép toán cộng(OR), 
nhân (AND) hay phép lấy bù (NOT).
Với các giá trị cho trước của các biến, hàm Boole có thể có giá trị 1 
hoặc 0.
Ví dụ :
zxyx)z,y,x(F +=
MSB
12-Sep-10
13
2. Phương pháp bảng chân trị
Để biểu diễn hàm Boole dưới dạng bảng chân trị, ta liệt kệ một danh sách
2n tổ hợp các giá trị 0 và 1 của các biến Boole và một cột chỉ ra giá trị của 
hàm F.
A B C F
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 0
Ví dụ:
3. Phương pháp dạng chuẩn 1
Minterm (Tích chuẩn): là tích số của đầy đủ các biến ở dạng bù hay
không bù. Nếu giá trị của biến là 0 thì biến sẽ ở dạng bù, còn nếu giá trị
của biến là 1 thì biến sẽ ở dạng không bù.
Với n biến có thể tạo ra 2n minterm.
Minterm được ký hiệu là mi, với i là tổ hợp nhị phân tạo bởi giá trị các
biến.
Ví dụ: Các minterm cho hàm 2 biến
A B
minterm
Biểu thức Ký hiệu
0
0
1
1
0
1
0
1
m0
m1
m2
m3
A
B
A B
A B
B
A
12-Sep-10
14
Dạng chuẩn 1
Dạng chuẩn 1: là dạng tổng của các tích chuẩn (SOP – Standard Sum-Of-
Products). Dạng chuẩn 1 có thể được tạo ra dễ dàng từ dạng tổng các tích.
Với: mi là minterm thứ i
Fi là giá trị của hàm F tương ứng với minterm thứ i.
Dạng chuẩn 1 có thể biểu diễn bằng nhiều cách khác nhau.
Bất kỳ hàm Boole nào cũng có thể biểu diễn ở dạng chuẩn 1.
∑
−
=
=
12
0i
ii
n
F.mF
Ví dụ
Hàm F sau được viết dưới dạng chuẩn 1:
DCBADABCDCBAABCD)D,C,B,A(F +++=
Ngoài ra, còn có nhiều cách để biểu diễn cho dạng chuẩn 1 của hàm trên:
DCBADABCDCBAABCD)D,C,B,A(F +++=
= 1111 + 1010 + 1110 + 0101
= m15 + m10 + m14 + m5
∑= )15,14,10,5(
12-Sep-10
15
Bất kỳ hàm Boole nào cũng có thể biểu diễn ở dạng chuẩn 1
CAAB)C,B,A(F +=
( )CBBA)CC(AB +++=
CBACBACABABC +++=
000010110111 +++=
0267 mmmm +++=
∑= )7,6,2,0(
Giải
Bất kỳ hàm Boole nào cũng có thể biểu diễn ở dạng chuẩn 1
)YX)(ZX()Z,Y,X(F ++=
YZZXXYXX +++=
YZ)XX(Z)YY(X)ZZ(XY +++++=
YZXXYZZYXYZXZXYXYZ +++++=
ZYXYZXZXYXYZ +++=
001011110111 +++=
1367 mmmm +++=
∑= )7,6,3,1(
Giải
12-Sep-10
16
3. Phương pháp dạng chuẩn 2
Maxterm (tổng chuẩn): là tổng số của đầy đủ các biến ở dạng bù hay không 
bù. Nếu giá trị của biến là 1 thì biến sẽ ở dạng bù, còn nếu giá trị của biến là 
0 thì biến sẽ ở dạng không bù.
Với n biến có thể tạo ra 2n Maxterm.
Maxterm được ký hiệu là Mi, với i là tổ hợp nhị phân tạo bởi giá trị các biến.
Ví dụ: Các Maxterm cho hàm 2 biến
A B
Maxterm
Biểu thức Ký hiệu
0
0
1
1
0
1
0
1
M0
M1
M2
M3
+A
B
+A B
+A B
B
+A
Ghi chú: Bù của minterm là Maxterm và ngược lại.
ii Mm = ii mM =
Ví dụ chứng minh:
m7 của hàm 3 biến: ABC
ABCm 7 =
7M=
CBA ++=
12-Sep-10
17
Dạng chuẩn 2: là dạng tích của các tổng chuẩn (POS – Standard –
Product-Of-Sums). Dạng chuẩn 2 có thể được tạo ra dễ dàng từ dạng tích
các tổng.
Với: Mi là Maxterm thứ i
Fi là giá trị của hàm F tương ứng với maxterm thứ i.
Dạng chuẩn 2 có thể biểu diễn bằng nhiều cách khác nhau.
Bất kỳ hàm Boole nào cũng có thể biểu diễn ở dạng chuẩn 2.
∏−
=
+=
12
0i
ii
n
)FM(F
Dạng chuẩn 2
Ví dụ
)DCBA)(DCBA)(DCBA()D,C,B,A(F +++++++++=
0110.0100.1011)D,C,B,A(F =
Hàm F sau được viết dưới dạng chuẩn 2:
Ngoài ra, còn có nhiều cách để biểu diễn cho dạng chuẩn 2 của hàm trên:
6411 M.M.M)D,C,B,A(F =
∏= )11,6,4()D,C,B,A(F
12-Sep-10
18
Bất kỳ hàm Boole nào cũng có thể biểu diễn ở dạng chuẩn 2
CAAB)C,B,A(F +=
Giải
)AA( +=
)CB)(BA)(CA( +++=
)CBAA)(CCBA)(CBBA( ++++++=
)CBA)(CBA)(CBA)(CBA)(CBA)(CBA( ++++++++++++=
)CBA)(CBA)(CBA)(CBA( ++++++++=
101.100.011.001=
5431 M.M.M.M=
∏= )5,4,3,1(
)CB( +)CA( + )BA( +
Bất kỳ hàm Boole nào cũng có thể biểu diễn ở dạng chuẩn 2
)YX)(ZX()Z,Y,X(F ++=
)ZZYX)(ZYYX( ++++=
)ZYX)(ZYX)(ZYX)(ZYX( ++++++++=
101.100.010.000=
5420 M.M.M.M=
∏= )5,4,2,0(
Giải
12-Sep-10
19
Một số ví dụ
Hãy biểu diễn các hàm sau dưới dạng biểu thức đại số:
∑= )7,6,5,4,1()C,B,A(F.a
∑= )7,6,5,4,1()D,C,B,A(F.b
∏= )7,3,2,0()Z,Y,X(F.c
∏= )7,3,2,0()T,Z,Y,X(F.d
4. TRƯỜNG HỢP TÙY ĐỊNH
Trong thực tế có những trường hợp một vài tổ hợp nhị phân của các biến
là không xảy ra. Do đó, giá trị của hàm tương ứng với những tổ hợp nhị
phân này có thể là 0 hay 1 đều được, người ta gọi đó là những trường hợp
tùy định (don’t care, viết tắt là d). Khi điền vào bảng chân trị những
trường hợp tùy định, ta dùng ký hiệu X.
Ví dụ:
∑ += )1(d)2,0()B,A(F
A B F
0
0
1
1
0
1
0
1 0
1
1
X
12-Sep-10
20
5. BÌA KARNAUGH 
Bìa K cho hàm 2 biến
F(A,B)
MSB
A
B 0 1
0
1 11
00
01
10
3
0 2
1
Bìa K cho hàm 3 biến
B 
f(A,B,C)
C
AB
00 01 11 10 
0 
1 C
A 
MSB
000 010 110 100
001 011 111 101
7
0
1
2
3
4
5
6
12-Sep-10
21
f(A,B,C,D)
CD
AB
00 01 11 10 
00 
01 
11 
10 
0 4
1 5
3 7
2 6
12 8
13 9
15 11
14 10
C 
A 
B
D
Bìa K cho hàm 4 biến
Bìa K cho hàm 5 biến
F
DE
BC
00 01 11 10 
00 
01 
11 
10 
0 4
1 5
3 7
2 6
12 8
13 9
15 11
14 10
10 11 01 00 
24 28
25 29
27 31
26 30
20 16
21 17
23 19
22 18
A = 0 A = 1
12-Sep-10
22
Cách điền vào bìa K
1. Nếu hàm F được biểu diễn dưới dạng chuẩn 1 (dạng ∑) thì ta điền 
giá trị 1 vào các ô có số thứ tự tương ứng với các minterm (tích 
chuẩn), điền X vào các ô ứng với các trường hợp tùy định và điền 0 
vào các ô còn lại.
Ta có thể chỉ điền vào bìa K hai ký hiệu 0 và X, hoặc 1 và X. Các ô 
bỏ trống được ngầm hiểu.
Ví dụ: ∑ += )7,4(d)6,3,1,0()C,B,A(F
00 01 11 10
0
1
AB
C
F
0
0 2 6 4
1 3 7 5
1
1 1
1 X
X
0
Cách điền vào bìa K
2. Nếu hàm F được biểu diễn dưới dạng chuẩn 2 (dạng ∏) thì ta điền 
giá trị 0 vào các ô có số thứ tự tương ứng với các minterm (tích 
chuẩn), điền X vào các ô ứng với các trường hợp tùy định và điền 1 
vào các ô còn lại.
Ta có thể chỉ điền vào bìa K hai ký hiệu 0 và X, hoặc 1 và X. Các ô 
bỏ trống được ngầm hiểu.
Ví dụ: ∏= )11,7,1(D).15,14,12,6,4,3()D,C,B,A(F
00 01 11 10
F AB
CD
00
01
11
10
0
0
0
0
0
0 1
X
X X
1
1 1
1
1
1
12-Sep-10
23
Cách điền vào bìa K
3. Nếu hàm F được biểu diễn dưới dạng bảng chân trị thì ta điền 0, 1 
hoặc X vào các ô có tổ hợp nhị phân trùng với tổ hợp nhị phân của bảng 
chân trị.
Ví dụ:
A B C F
0 0 0 1
0 0 1 X
0 1 0 X
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1
00 01 11 10
0
1
AB
C
F
1
1
1X
X
00 01 11 10
0
1
AB
C
F
0
0 0
X
X
Cách điền vào bìa K
4. Nếu hàm Boole được cho dưới dạng tổng của các tích không chuẩn.
+= DCBA)D,C,B,A(F
00 01 11 10
F
AB
CD
00
01
11
10
1 1 1
1
1
1
1
1
1
+DBA +DCB DC
1110
01X0 0100
0110
X101 0101
1101
XX11
0011
0111
1011
1111
12-Sep-10
24
Cách điền vào bìa K
5. Nếu hàm Boole được cho dưới dạng tích của các tổng không chuẩn.
B)CA)(DCBA()D,C,B,A(F ++++=
00 01 11 10
F
AB
CD
00
01
11
10
0100
1X0X
1000
1001
1100
1101
X0XX
0000
0001
0010
0011
1000
1001
1010
10110
0 0
0
0
0
0
0
0
0
0
7.5 RÚT GỌN HÀM BOOLE BẰNG BÌA KARNAUGH 
1. Định nghĩa các ô kế cận:
Hai ô được gọi là kế cận nhau, nếu chúng ứng với 2 minterm hoặc 2 
maxterm, chỉ khác nhau ở 1 biến.
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10 0
1 1 0
12-Sep-10
25
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
1 1 1 1
1 1
1 1
1 1
1 1
1 
1
1 
1
Bốn ô kế cận: gồm 2 nhóm 2 ô kế cận
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
0 0 0 0
0 0
0 0
0 0
0 0
0 
0
0 
0
Bốn ô kế cận: gồm 2 nhóm 2 ô kế cận
12-Sep-10
26
Bốn ô kế cận: gồm 2 nhóm 2 ô kế cận
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
1 1 1 1
1 1
1 1
1 1
1 1
1 
1
1 
1
Bốn ô kế cận: gồm 2 nhóm 2 ô kế cận
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
0 0 0 0
0 0
0 0
0 0
0 0
0 
0
0 
0
12-Sep-10
27
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
1 1 1 1
0 0
0 0
1 1 1 1
1 1 1 1
1 1 1 1
0 0
0 0
0 0 0 0
0 0 0 0
Tám ô kế cận: gồm 2 nhóm 4 ô kế cận
Việc gom các ô kế cận
- Khi gom 2n ô kế cận có cùng giá trị 1, ta được 1 tích.
- Gom 2n ô ta loại đươc n biến biến.
- Các biến giống nhau còn lại được ghi dưới dạng bù, nếu nó có giá trị 
bằng 0, ngược lại sẽ được ghi dưới dạng không bù.
- Khi gom 2n ô kế cận có cùng giá trị 0, ta được 1 tổng. Các biến sẽ được 
ghi theo qui ước ngược lại với dạng tích.
00 01 11 10
F
AB
CD
00
01
11
10
1 1 DCB
0 0 DCA ++
12-Sep-10
28
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
1 1 1 1
1 1
1 1
1 1
1 1
1 
1
1 
1
Các ví dụ
DC
DA
DA
DB
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
0 0 0 0
0 0
0 0
0 0
0 0
0 
0
0 
0
Các ví dụ
DC +
DA +
DA +
DB +
12-Sep-10
29
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
0 0 0 0
0 0
0 0
0 0
0 0
0 
0
0 
0
Các ví dụ
DC +
CA +
DB +
CB +
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
1 1 1 1
1 1
1 1
1 1
1 1
1 
1
1 
1
Các ví dụ
DC
CA
DB
CB
12-Sep-10
30
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
00 01 11 10
F
AB
CD
00
01
11
10
1 1 1 1
0 0
0 0
1 1 1 1
1 1 1 1
1 1 1 1
0 0
0 0
0 0 0 0
0 0 0 0
Các ví dụ
C
DD
A
Rút gọn hàm sau
00 01 11 10
F AB
CD
00
01
11
10
1
11
1
1
1
1
=)D,C,B,A(F BA + CB+DCBA
12-Sep-10
31
Rút gọn hàm sau
∑= )15,14,7,6,5,4,1,0()D,C,B,A(F
00 01 11 10
F
AB
CD
00
01
11
10
1
1
1
1
1
1
1
1
=)D,C,B,A(F CA + CB
Rút gọn hàm sau
∏= )15,13,12,11,9,6,4,2,0()D,C,B,A(F
00 01 11 10
F
AB
CD
00
01
11
10 0
0 00
0
0
0
0
=)D,C,B,A(F )DA( + )DA( +
0
)DCB( ++
=)D,C,B,A(F )DA( + )DA( + )CBA( ++
12-Sep-10
32
Rút gọn hàm sau
∑ += )9,7,6(d)11,3,2,1,0()D,C,B,A(F
00 01 11 10
F
AB
CD
00
01
11
10 1
1
X
X
1
1 X
=)D,C,B,A(F BA +
1
DB
Rút gọn hàm sau
∑= )14,13,12,9,8,6,5,4,2,1,0()D,C,B,A(F
00 01 11 10
F
AB
CD
00
01
11
10 1
1 1 1 1
1 1
=)D,C,B,A(F DA +
1
DB
1
1 1
C +
12-Sep-10
33
Rút gọn hàm sau
CBADCBADCBCBA)D,C,B,A(F +++=
00 01 11 10
F
AB
CD
00
01
11
10 1
1 1
1 1
1 1
=)D,C,B,A(F DB + DCACB +
000X
X010 0110
100X
1. Cấu trúc AND-OR
Sơ đồ logic AND-OR được tạo ra từ hàm Boole có dạng 
tổng các tích.
Ví dụ:
7.6 CÁC PHƯƠNG PHÁP THỰC HIỆN HÀM BOOLE BẰNG SƠ ĐỒ LOGIC
DCBBA)D,C,B,A(F +=
A B C D
F
12-Sep-10
34
Sơ đồ logic OR - AND được tạo ra từ hàm Boole có dạng 
tích các tổng.
Ví dụ:
)DCA)(BA()D,C,B,A(F +++=
A B C D
2. Cấu trúc OR – AND 
F
Ví dụ:
DACBA)D,C,B,A(F +=
B C D
3. Cấu trúc NAND – NAND 
DACBA)D,C,B,A(F +=
DAC.BA)D,C,B,A(F =
F
A
12-Sep-10
35
)DCA)(BA()D,C,B,A(F +++=
B C D
4. Cấu trúc NOR – NOR 
)DCA)(BA()D,C,B,A(F +++=
)DCA()BA()D,C,B,A(F ++++=
A
F