Bài giảng Kỹ thuật điện - Chương 3: Phương pháp phân tích và giải mạch điện
- Phân tích mạch điện là bài toán cho biết thông số và kết cấu của
mạch điện, cần tìm dòng điện, điện áp, công suất trên các nhánh.
- Có nhiều phương pháp khác nhau để phân tích mạch điện. Việc
chọn phương pháp tùy thuộc và sơ đồ cụ thể.
- Hai định luật Kiếchốp là cơ sở để giải mạch điện.
- Giải mạch điện sin ở chế độ xác lập gồm các bước sau:
+ Biểu diễn dòng điện, điện áp dưới dạng véctơ, số phức.
+ Lập phương trình theo định luật Kiếchốp.
+ Giải hệ hương trình đã lập tìm giá trị dòng điện và điện áp.
- Đối với mạch dòng điện không đổi ở chế độ xác lập, xem đó là
trường hợp riêng của dòng điện sin với tần số = 0.
+ Nhánh có điện dung C coi như hở mạch (vì 1/C =)
+ Nhánh có điện cảm L coi như nối tắt (vì L=0).
+ Mạch chỉ còn điện trở, việc giải sẽ đơn giản hơn rất nhiều
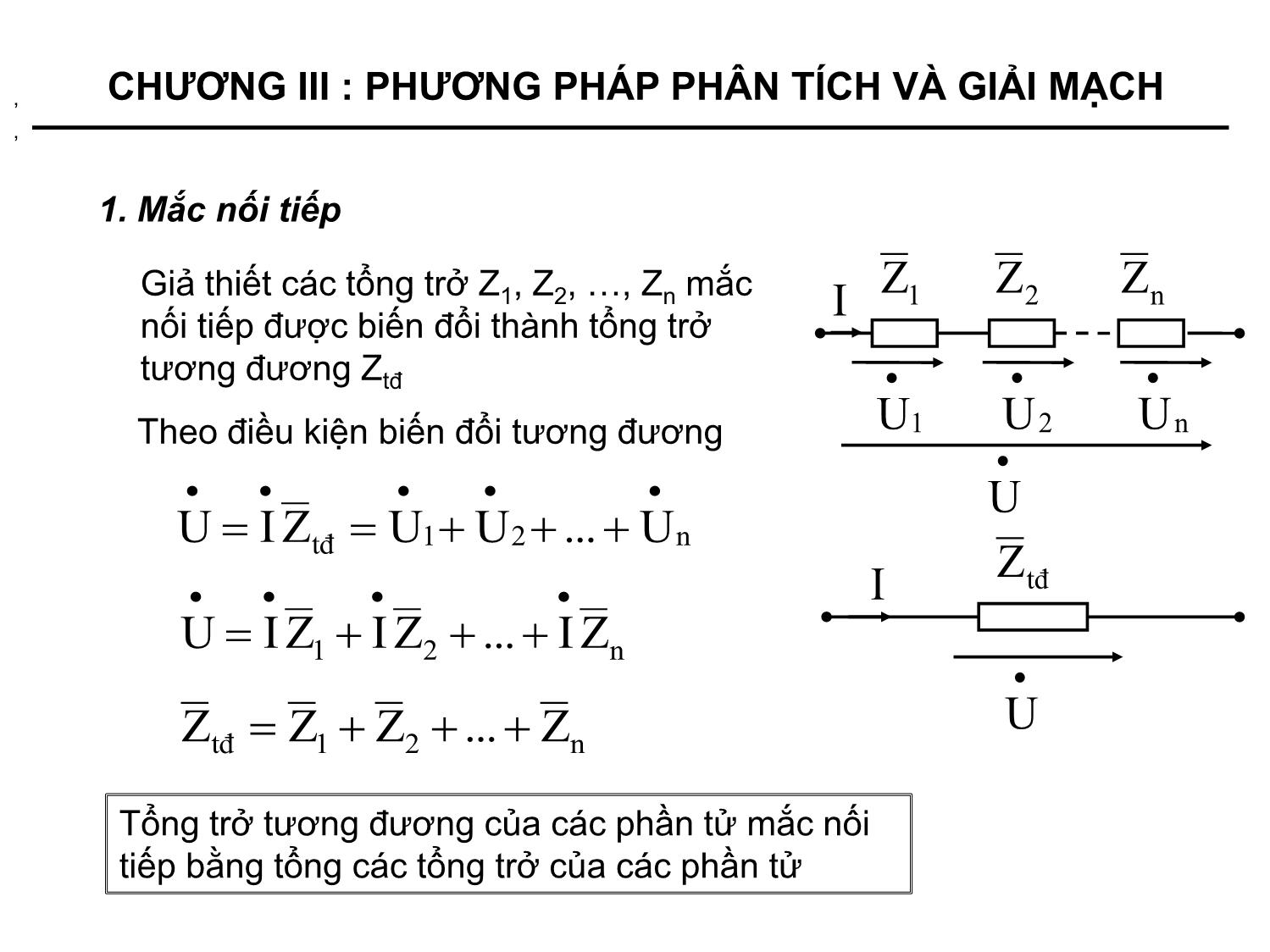
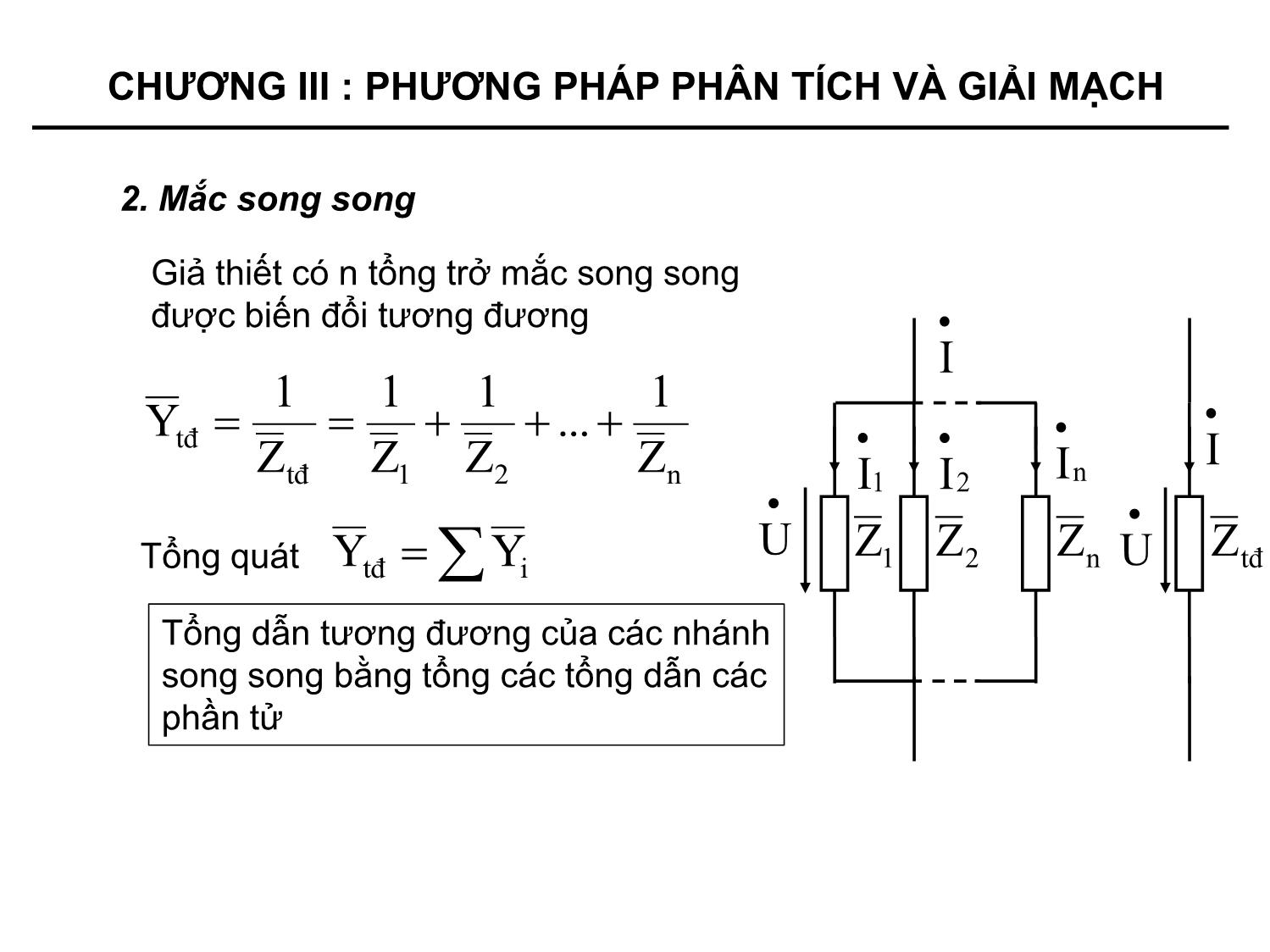
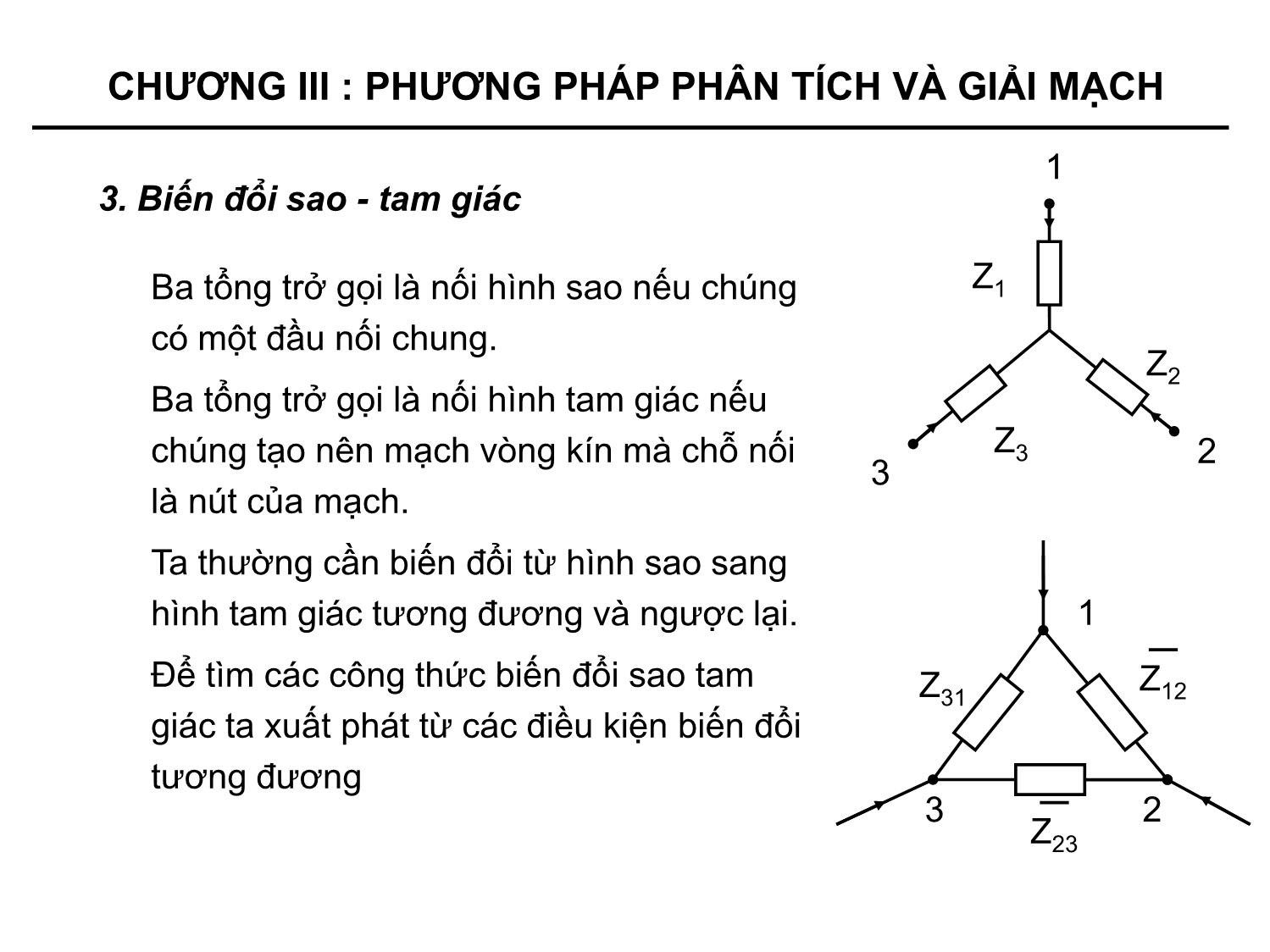
Phương pháp biến đổi tương đương
- Biến đổi mạch điện nhằm mục đích đưa mạch phức tạp về dạng
đơn giản hơn.
- Biến đổi tương đương là biến đổi mạch điện sao cho dòng điện,
điện áp tại các bộ phận không bị biến đổi vẫn giữ nguyên.
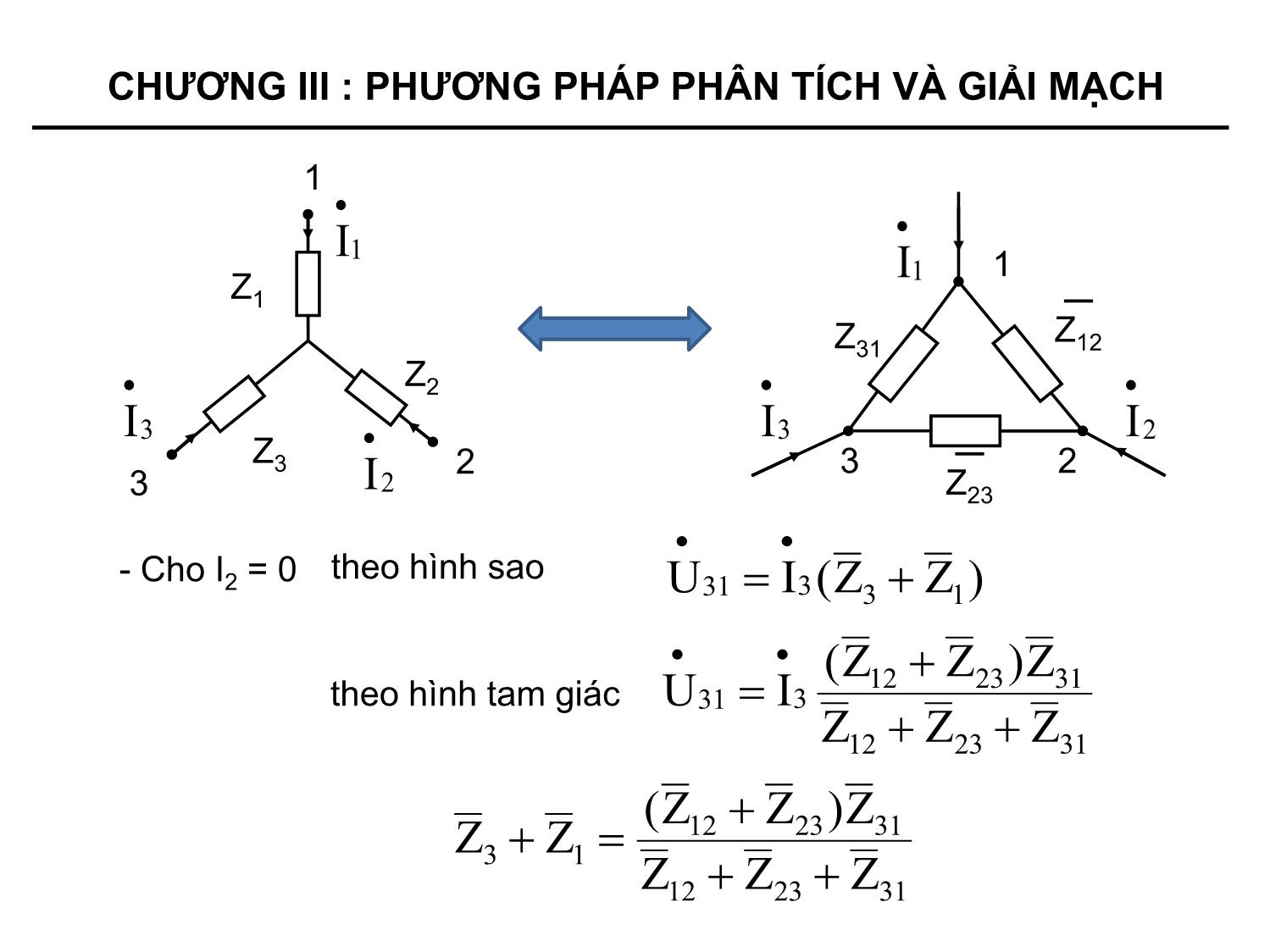
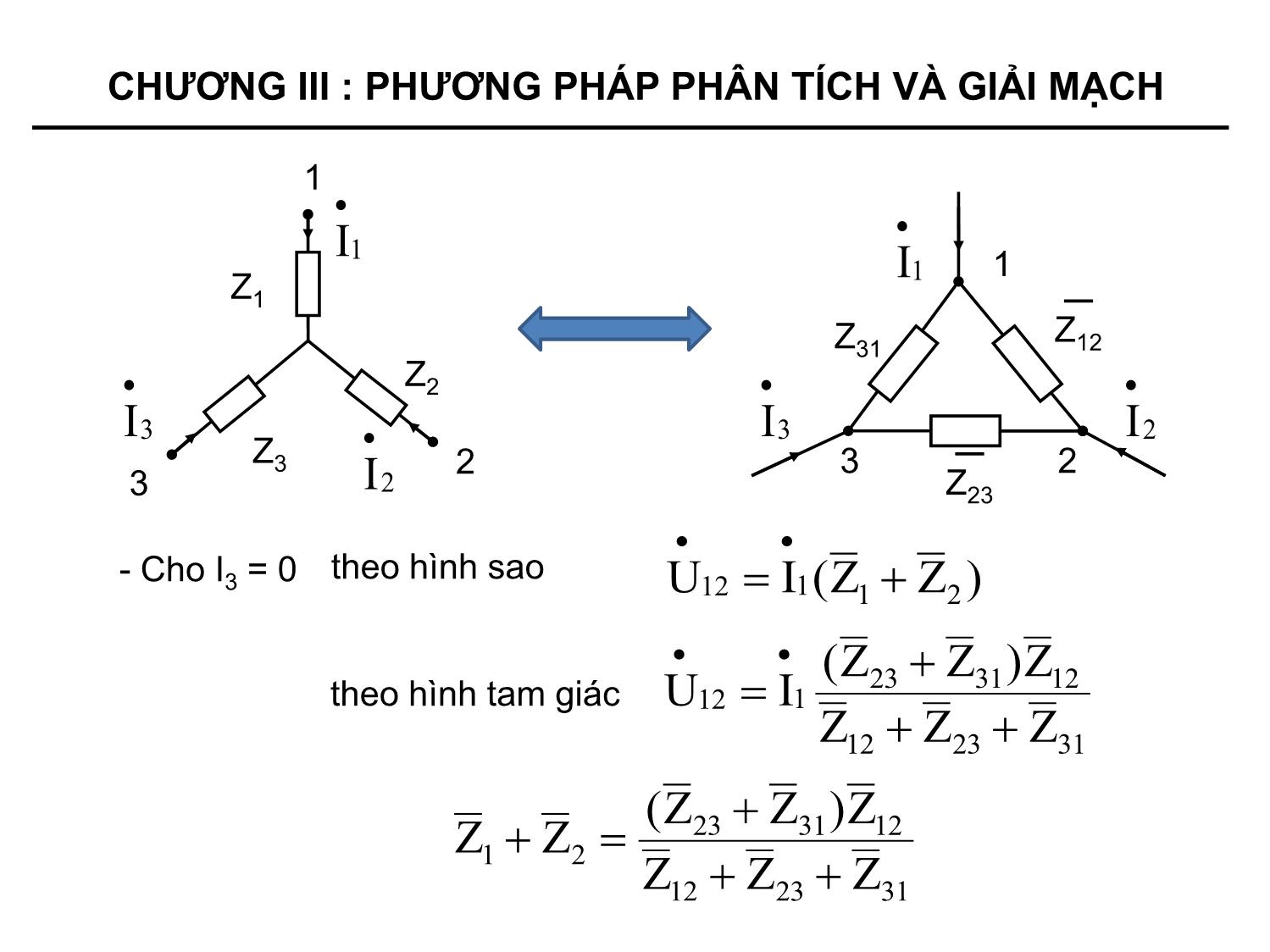
- Một số biến đổi thường gặp:
+ Mắc nối tiếp
+ Mắc song song
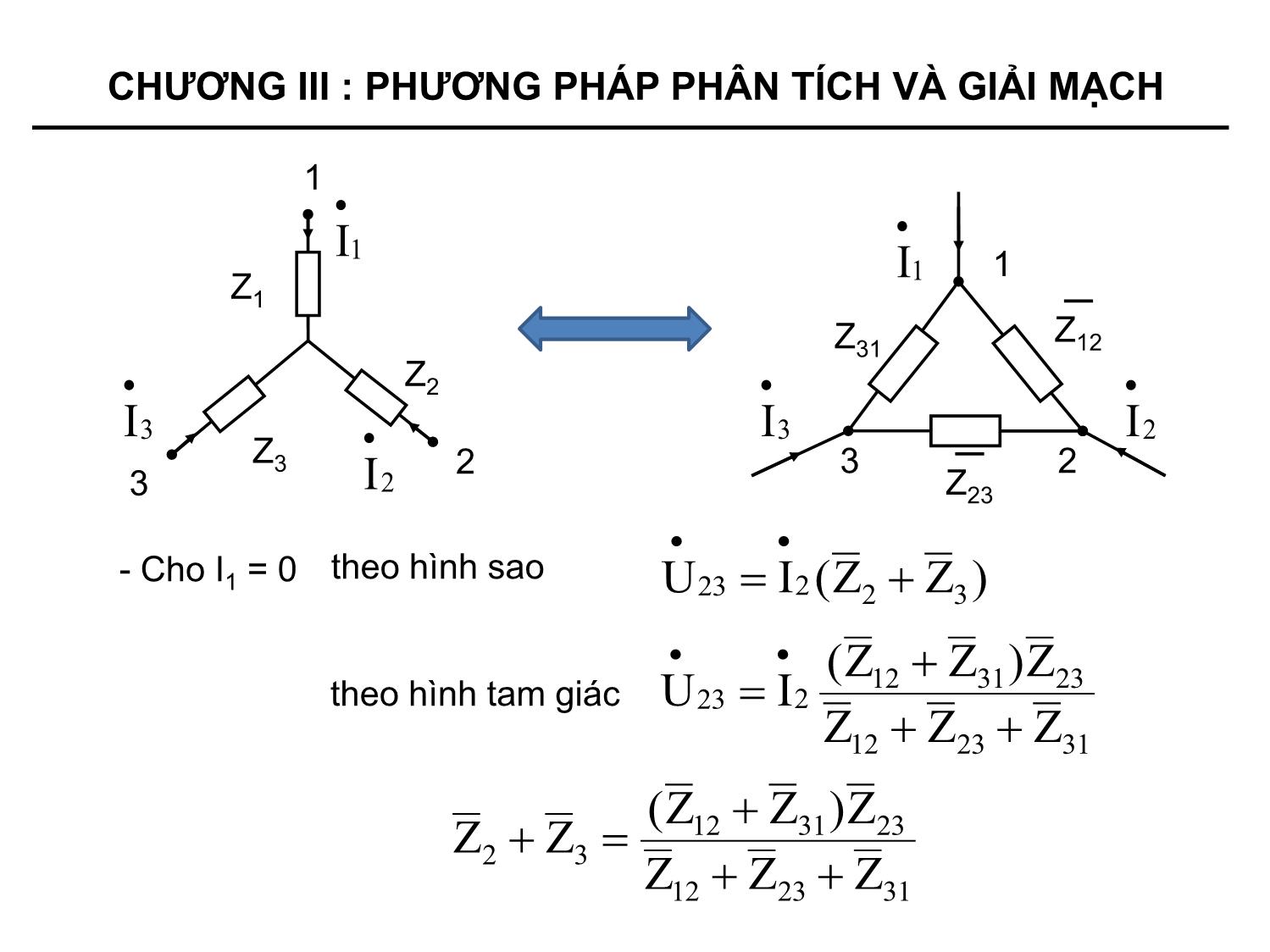
+ Đổi nối tam giác – sao
+ Đổi nối sao – tam giác

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5

Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật điện - Chương 3: Phương pháp phân tích và giải mạch điện

ìm dòng điện nhánh Áp dụng giải mạch điện với tsin2120ee 31 2j2ZZZ 321 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH 25,0j25,0 8 2j2 2j2 1 YYY 321 120EE 31 80 )25,0j25,0(3 2).25,0j25,0(120 YYY YEYE U 321 3311 AB 10j10 2j2 12080 I1 20j20 2j2 80 I2 10j10 2j2 12080 I3 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH V. Phương pháp xếp chồng Phương pháp này rút ra từ tính chất cơ bản của hệ phương trình tuyến tính: trong mạch điện tuyến tính nhiều nguồn, dòng điện qua mỗi nhánh bằng tổng đại số các dòng điện qua nhánh do tác dụng riêng rẽ của từng sức điện động (lúc đó các sức điện động khác được coi bằng không); Điện áp trên mỗi nhánh cũng bằng tổng đại số các điện áp gây nên trên nhánh do tác dụng riêng rẽ từng sức điện động CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Cho mạch điện hình bên, có R=2, XL=2. Nguồn sin E1=E2=120 V. Tìm dòng điện nhánh Ví dụ: Sử dụng phương pháp xếp chồng: Ở đây cần giải mạch điện hình bên, ta sẽ giải hai mạch điện, trong mỗi mạch chỉ có một sức điện động tác dụng riêng rẽ và sau đó xếp chồng (cộng đại số) các kết quả của mỗi mạch CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Giải mạch điện I: Biến đổi tương đương: vì j1Z 2 1 Z23 2j2ZZZZ 321 3j3ZZZ 23tđ 20j20 j33 120 Z E I tđ ' 1 10j10 2 I II ' 1' 3 ' 2 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Giải mạch điện II tương tự mạch điện I: 20j20 j33 120 Z E I tđ '' 3 10j10 2 I II '' 3'' 2 '' 1 Xếp chồng các kết quả: 10j10III ''2 ' 11 2101010I 221 10j10III ''2 ' 22 20j20III '3 '' 33 2101010I 222 2202020I 223 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH VI. Phương pháp tính mạch có nguồn chu kỳ không sin Trong kỹ thuật điện, điện tử thường gặp các nguồn chu kỳ không sin. Ví dụ: Điện áp sau chỉnh lưu hai nửa chu kỳ Điện áp hình răng cưa Điện áp hình chữ nhật Để phân tích các mạch không sin ta áp dụng nguyên lý xếp chồng. Dùng các công thức phân tích Furiê phân tích nguồn không sin thành tổng các điều hòa có tần số khác nhau CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Trong đó: E0 - thành phần một chiều E1msin(t+ 1) - thành phần cơ bản có tần số bằng tần số nguồn không sin E2msin(2t+ 2) - thành phần bậc hai có tần số 2 Ekmsin(kt+ k) - thành phần bậc k có tần số k )tksin(E ...)t2sin(E)tsin(EE)t(e 2mk 22m11m0 Như vậy bài toán mạch có nguồn chu kỳ không sin trở thành nhiều bài toán mạch xoay chiều. Đối với mỗi thành phần điều hòa ta có thể dùng các phương pháp đã nghiên cứu ở các mục trên. CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Lưu ý là tổng trở của các phần tử phụ thuộc vào tần số: Cảm kháng với điều hòa bậc k: 1LLk kXLkX Dung kháng với điều hòa bậc k: 1CCk X k 1 Ck 1 X Tổng trở với với điều hòa bậc k: 22 k ) Ck 1 Lk(RZ R Ck 1 Lk arctgk CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Thuật toán giải mạch có nguồn chu kỳ không sin như sau: Bước 1: Phân tích nguồn chu kỳ không sin thành tổng các điều hòa có tần số khác nhau Bước 2: Cho từng điều hòa tác động, tìm dòng điện, điện áp do từng điều hòa tạo nên. Bước 3: Tổng hợp kết quả. Chú ý là vì các điều hòa có tần số khác nhau nên cần dùng biểu thức dạng tức thời )tksin(i ...)t2sin(i)tsin(iI)t(i 2mk 22m11m0 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Trị số hiệu dụng của dòng điện không sin T 0 k210 T 0 2 dt)i...iiI( T 1 dti T 1 I 2 k 2 2 2 1 2 0 I...IIII CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Ví dụ: Nguồn không sin )30t3sin(230tsin2100100)t(e o Tác động vào mạch tải có R=4Ω và XL1=3Ω. Hãy tìm dòng điện hiệu dụng và tức thời Cho từng thành phần điều hòa tác động Bài giải: Thành phần một chiều A25 4 100 R E I 00 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Thành phần bậc nhất A20 34 100 Z E I 22 1 1 o1L 37 4 3 arctg R X arctg )37tsin(220i o1 Thành phần bậc ba A3 94 100 Z E I 22 3 3 o3L 3 66 4 9 arctg R X arctg )66t3sin(23i o3 9L3X 3L CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH )66t3sin(23)37tsin(22025)t(i oo Dòng điện Giá trị hiệu dụng A15,3232025IIII 22223 2 1 2 0 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH VII. Các ví dụ Ví dụ 1: Cho mạch hình 3-12. Biết U = 230V, R1 = R2 = 0,5 , R3 = 8, R4 = 12, R5 = R6 = 1, R7 = 2, R8 = 15, R9 = 10, R10 = 20. Tìm dòng điện trong các nhánh Ta giải bằng phương pháp biến đổi tương đương. Lần lượt thực hiện biến đổi nối tiếp và song song. Điện trở tương đương có chỉ số là tổng các chỉ số thành phần Bài giải CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH R9 nối tiếp R10 → R11 302010RRR 10911 R11 song song R8 → R12 10 3015 30.15 RR RR R 811 811 12 R12 nối tiếp R7 → R13 12210RRR 71213 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH R13 song song R4 → R14 6 1212 12.12 RR RR R 413 413 14 R14 nối tiếp R5 và R6 → R15 8116RRRR 651415 R15 song song R3 → R16 4 88 8.8 RR RR R 315 315 16 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH R16 nối tiếp R1 và R2 → Rtđ 55,05,04RRRR 2116tđ Dòng điện các nhánh A46 5 230 R U II tđ 21 A23 88 8 46 RR R II 315 15 13 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH A23 88 8 46 RR R II 315 15 13 A23II 65 A5,11 1212 12 23 RR R II 413 4 67 A5,11 1212 12 23 RR R II 413 13 64 A67,7 1530 30 5,11 RR R II 811 11 78 A83,3 1530 15 5,11 RR R III 811 8 7109 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Ví dụ 2: Cho mạch xoay chiều hình bên )45tsin(250e o1 )135tsin(250e o2 6 C 1 L 2 1 8RR 21 125,3R3 Giải mạch điện bằng các phương pháp: Dòng điện nhánh, dòng điện vòng, điện áp nút CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Phương pháp dòng điện nhánh Chọn chiều dòng điện trong các nhánh và chiều đi vòng như hình vẽ. Biểu diễn dạng phức của nguồn và các tải như sau: 4,35j4,354550E o1 4,35j4,3513550E o2 6j8LjRZ 111 6j8 C 1 jRZ 2 22 125,3RZ 33 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Lập hệ phương trình 23322 13311 321 EZIZI EZIZI 0III Thay số vào hệ phương trình )5,34j5,34(I125,3I)6j8( 5,34j5,34I125,3I)6j8( 0III 32 31 321 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH )5,34j5,34I125,3I)6j8( 5,34j5,34I125,3I)6j8( 0III 32 31 321 Giải hệ bằng phương pháp định thức 125,36j80 125,306j8 111 )6j8(125,3)125,3)(6j8()6j8)(6j8(1 150503664 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH 292j8,716 125,36j85,34j5,34 125,305,34j5,34 110 1 8,716j292 125,35,34j5,340 125,35,34j5,346j8 101 2 95,1j78,4 150 292j8,716 I 11 Dòng điện 16,595,178,4I 221 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH 83,2j83,2III 213 78,4j95,1 150 8,716j292 I 22 16,578,495,1I 222 483,283,2I 223 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Phương pháp dòng điện vòng Chọn chiều dòng điện trong các nhánh và dòng điện vòng Ia và Ib tại vòng a và b như hình vẽ. Biểu diễn dạng phức của nguồn và các tải như sau: 4,35j4,354550E o1 4,35j4,3513550E o2 6j8LjRZ 111 6j8 C 1 jRZ 2 22 125,3RZ 33 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH 232b3a 13b31a E)ZZ(IZI EZI)ZZ(I Lập hệ phương trình )5,34j5,34(I)6j125,11(I125,3 5,34j5,34I125,3I)6j125,11( ba ba Thay số vào hệ phương trình )5,34j5,34I)6j125,11(I125,3 5,34j5,34I125,3I)6j125,11( ba ba CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Giải bằng định thức 150 6j125,11125,3 125,36j125,11 292j8,716 6j125,115,34j5,34 125,35,34j5,34 1 8,716j292 5,34j5,34125,3 5,34j5,346j125,11 2 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Dòng điện vòng 95,1j78,4 150 292j8,716 I 1a 78,4j95,1 150 8,716j292 I 2b Dòng điện nhánh 95,1j78,4II a1 16,595,178,4I 221 16,578,495,1I 222 483,283,2I 223 78,4j95,1II b2 83,2j83,2III ba3 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Phương pháp điện áp nút Chọn chiều dòng điện trong các nhánh như hình vẽ. Biểu diễn dạng phức của nguồn và các tải như sau: 4,35j4,354550E o1 4,35j4,3513550E o2 6j8LjRZ 111 6j8 C 1 jRZ 2 22 125,3RZ 33 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Tổng dẫn phức các nhánh 06,0j08,0 100 6j8 6j8 1 Z 1 Y 1 1 06,0j08,0 100 6j8 6j8 1 Z 1 Y 2 2 32,0 125,3 1 Z 1 Y 3 3 Điện áp nút UAB 321 2211 AB YYY YEYE U CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH 32,006,0j08,006,0j08,0 )06,0j08,0)(5,34j5,34()06,0j08,0)(5,34j5,34( UAB 83,8j83,8 48,0 12,0j)5,34j5,34( UAB Dòng điện nhánh 95,1j78,4 6j8 5,34j5,34)83,8j83,8( Z EU I 1 1AB 1 78,4j95,1 6j8 5,34j5,34)83,8j83,8( Z EU I 2 2AB 2 83,2j83,2 125,3 83,8j83,8 Z U I 3 AB 3 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Trị số hiệu dụng 16,595,178,4I 221 16,578,495,1I 222 483,283,2I 223 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Một cuộn dây có điện trở R=10, điện cảm L=35mH được đặt vào điện áp u=59,6sint+10,7sin3t-1,97sin7t V, =314rad/s - Tìm biểu thức dòng điện trong mạch - Xác định hệ số công suất của mạch Ví dụ 2: Bài giải: - Điện áp không sin được phân tích thành các thành phần điều hòa bậc 1, 3 và 7. - Dùng phương pháp xếp chồng với từng thành phần: CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Dòng điện thành phần cơ bản o o o 1 m1 m1 4701,4 479,14 06,59 Z U I Cho thành phần điều hòa cơ bản tác động: Tổng trở với tần số 99,10j10LjRZ1 o 1 479,14Z )47tsin(01,4i o1 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Dòng điện thành phần bậc 3 o o o 3 m3 m3 7331,0 7357,34 07,10 Z U I Cho thành phần điều hòa bậc 3 tác động: Tổng trở với tần số 3 97,32j10L3jRZ3 o 3 7357,34Z )73tsin(31,0i o3 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Dòng điện thành phần bậc 7 o o o 7 m7 m7 82025,0 826,77 091,1 Z U I Cho thành phần điều hòa bậc 7 tác động: Tổng trở với tần số 7 93,76j10L7jRZ7 o 7 826,77Z )82tsin(025,0i o7 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Dòng điện của mạch )73tsin(31,0)73tsin(31,0)47tsin(01,4i ooo 85,2 2 025,031,001,4 2 III I 2222 m7 2 m3 2 m1 Điện áp của mạch 42 2 97,17,106,59 2 UUU U 2222 m7 2 m3 2 m1 Công suất 8,801085,2RIP 22 Hệ số công suất 67,0 85,2.42 8,80 UI P cos CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH VIII. Bài tập chương III Bài số 3.1: Tính điện trở tương đương của mạch điện sau ở các cực. Biết R1=2; R2=2; R3=4; R4=6; R5=5. a) A-B b) A-C c) B-C d) A-D CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Bài giải: a) A-B: (R1 nối tiếp R2) song song (R3 nối tiếp R4) song song R5 5 1 10 1 4 1 R 1 RR 1 RR 1 R 1 54321AB 82,1RAB a) A-C: (((R1 nối tiếp R2) song song R5) nối tiếp R4)) song song R3 4RRR 2112 22,2 54 5.4 RR RR R 512 512 125 22,8622,2RRR 41251254 69,2 422,8 4.22,8 RR RR R 31254 31254 AC CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH c) B-C: (((R2 nt R1) // R5) nt R3) // R4 4RRR 1221 22,2 54 5.4 RR RR R 521 521 215 22,6422,2RRR 32152153 054,3 622,6 6.22,6 RR RR R 42153 42154 BC d) A-D: (((R3 nt R4) // R5) nt R2) // R1 10RRR 4334 33,3 510 5.10 RR RR R 534 534 345 33,5233,3RRR 23453452 45,1 233,5 2.33,5 RR RR R 13452 13452 AD CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Dùng phương pháp dòng điện mạch nhánh và dòng điện mạch vòng giải mạch điện có dạng như hình bên. Biết: E1=18V; E2=E3=5V; E4=15V; E5=3V R1=1; R2=2; R6=5; R3=R4=R5=1 Bài số 3.2: Bài giải: - Giả thiết chiều dòng điện trong các nhánh trùng với chiều sđđ, riêng nhánh 6 từ nút phía trên → phía dưới. - Mạch điện có 6 nhánh và 4 nút CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Giải theo phương pháp dòng điện nhánh: Lập hệ pt (vì mạch chỉ gồm điện trở nên ta không dùng dạng phức): 543554433 42664422 51665511 654 531 621 EEERIRIRI EERIRIRI EERIRIRI 0III 0III 0III CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH 13III 20I5II2 21I5II 0III 0III 0III 543 642 651 654 531 621 Thay số vào hệ pt và giải: 79,0I 71,7I 91,6I 61,1I 53,8I 32,9I 6 5 4 3 2 1 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Giải theo phương pháp dòng điện vòng Số vòng độc lập: 6-4+1=3 - Vòng 1 (Iv1) qua các nhánh 1, 6, 5 - Vòng 2 (Iv2) qua các nhánh 2, 4, 6 - Vòng 3 (Iv3) qua các nhánh 3, 5, 4 Các vòng đều thuận chiều kim đồng hồ 5435433v42v51v 4243v6422v61v 5153v62v6511v EEE)RRR(IRIRI EERI)RRR(IRI EERIRI)RRR(I Lập hệ pt: CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH 13I3II 20II8I5 21II5I7 3v2v1v 3v2v1v 3v2v1v Thay số vào hệ pt và giải: 61,1I 53,8I 32,9I 3v 2v 1v 79,0III 71,7III 92,6III 61,1II 53,8II 32,9II 2v1v6 3v1v5 3v2v4 3v3 2v2 1v1 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Giải mạch điện hình bên bằng phương pháp dòng điện vòng và phương pháp điện áp nút. Biết: E1=140V; E2=80V; E3=160V; R1=R3=0,5; R2=1; R4=R5=R6=3 Bài số 3.3. - Giả thiết chiều dòng điện trong các nhánh 1, 2, 3 trùng với chiều sđđ, các nhánh 4, 5, 6 theo chiều kim đồng hồ. Bài giải: CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH - Mạch điện có 6 nhánh và 4 nút → Số vòng độc lập : 3 (vòng 1 qua nhánh 1, 2, 4; vòng 2 qua nhánh 2, 3, 6; vòng 3 qua nhánh 4, 5, 6) - Chiều các dòng điện vòng cùng chiều kim đồng hồ Giải theo phương pháp dòng điện vòng 0)RRR(IRIRI EERI)RRR(IRI EERIRI)RRR(I 6543v62v41v 3263v6322v21v 2143v22v4211v Lập hệ pt: CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH Thay số vào hệ pt và giải: 0I9I3I3 80I3I5,4I 60I3II5,4 3v2v1v 3v2v1v 3v2v1v 4,4I 4,19I 1,6I 3v 2v 1v 15III 4,4II 5,10III 4,19II 5,25III 1,6II 3v2v6 3v5 3v1v4 2v3 1v2v2 1v1 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH - Biến đổi Δ (R4, R5, R6) → Y (RY1, RY2, RY3). - Mạch điện có hai nút A, B (trái qua phải) - Vì R4=R5=R6 = 3Ω nên RY1=RY2=RY3 = 1Ω Giải theo phương pháp điện áp nút 67,0 15,0 1 YY 31 Tổng dẫn các nhánh 5,0 11 1 Y2 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH 130 YYY YEYEYE U 321 332211 BA Điện áp nút: Dòng điện nhánh: 67,6 15,0 130140 RR UE I 1Y1 BA1 1 25 11 13080 RR UE I 2Y2 BA2 2 20 15,0 130160 RR UE I 3Y3 BA3 3 CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH CHƯƠNG III : PHƯƠNG PHÁP PHÂN TÍCH VÀ GIẢI MẠCH
File đính kèm:
 bai_giang_ky_thuat_dien_chuong_3_phuong_phap_phan_tich_va_gi.pdf
bai_giang_ky_thuat_dien_chuong_3_phuong_phap_phan_tich_va_gi.pdf

