Bài giảng Kỹ thuật điện 1 - Chương 7: Mạng hai cửa tuyến tính - Nguyễn Việt Sơn
Trong các chương trước ta đã học:
Các phương pháp số phức xét mạch tuyến tính hệ số hằng ở chế độ xác lập điều hòa:
Phương pháp dòng nhánh.
Phương pháp dòng vòng.
Phương pháp thế đỉnh.
Cách tính đáp ứng của mạch tuyến tính khi nguồn là kích thích chu kỳ không điều hòa.
Xét các quan hệ tuyến tính của mạch tuyến tính, từ đó xây dựng mô hình mạng một cửa
Kirchhoff tuyến tính.
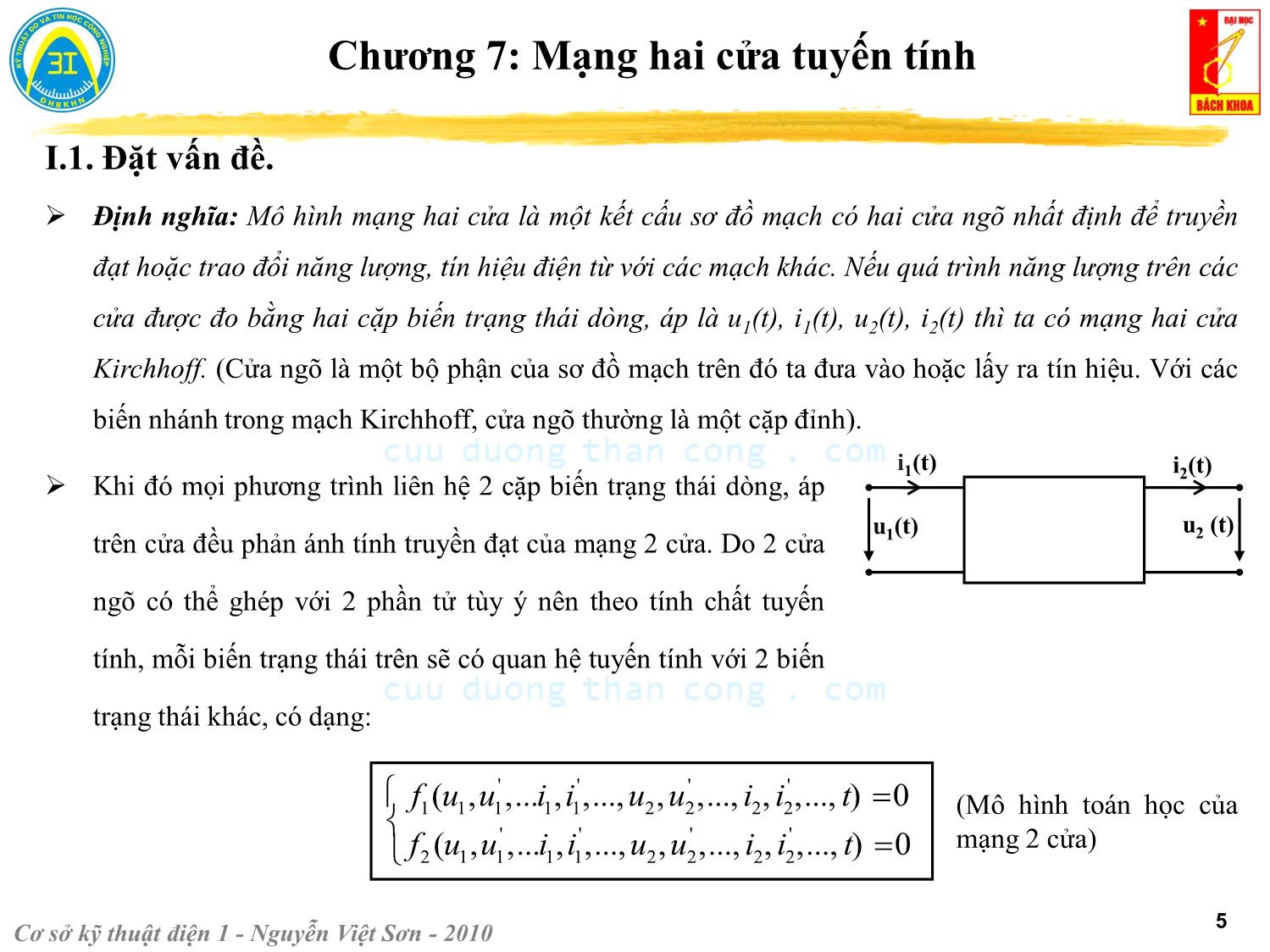
Trong chương này ta sẽ xây dựng thêm một sơ đồ cấu trúc mới, gọi là mô hình mạng hai cửa
Kirchhoff.
Thế nào là mạng 2 cửa ???
Tại sao ta phải xây dựng mô hình mạng 2 cửa ???

Trang 1

Trang 2

Trang 3

Trang 4
Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kỹ thuật điện 1 - Chương 7: Mạng hai cửa tuyến tính - Nguyễn Việt Sơn", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật điện 1 - Chương 7: Mạng hai cửa tuyến tính - Nguyễn Việt Sơn

I Chú ý: Với mạng 2 cửa tuyến tính tương hỗ ta có 12 21G G 1G H Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 26 Chương 7: Mạng hai cửa tuyến tính II.7. Ma trận của hệ các mạng hai cửa. a. Mạng hai cửa nối xâu chuỗi. A1 A2 An 1 n k k A A Ví dụ: Tính bộ số A của mạng 2 cửa hình π. Zn2 Zd Zn1 2I 2U 1U 1I Zd An2AdAn1 1 2 1 2 1 . 0 1 dU Z U I I 2U 1U Zn1 2I 1I 1 2 1 2 1 1 0 .1 1 n U U I IZ 1 2. .n d nA A A A 2 1 2 1 2 1 1 1 1 1 . d d n d d n n n n n Z Z Z A Z Z Z Z Z Z Z Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 27 Chương 7: Mạng hai cửa tuyến tính II.7. Ma trận của hệ các mạng hai cửa. b. Mạng hai cửa ghép nối tiếp. Hai mạng 2 cửa ghép được gọi là ghép nối tiếp nếu dòng điện chảy vào mạng thứ nhất bằng dòng điện chảy vào mạng thứ 2, dòng điện chảy ra mạng thứ nhất bằng dòng điện chảy ra mạng thứ 2. Z1 Z2 1 2Z Z Z Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 28 Chương 7: Mạng hai cửa tuyến tính II.7. Ma trận của hệ các mạng hai cửa. c. Mạng hai cửa ghép song song. Hai mạng 2 cửa ghép được gọi là ghép song song nếu chúng có chung đầu vào và đầu ra. 1 2Y Y Y Y1 Y2 Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 29 Chương 7: Mạng hai cửa tuyến tính II.7. Ma trận của hệ các mạng hai cửa. d. Mạng hai cửa ghép nối tiếp - song song. 1 2H H H H1 H2 e. Mạng hai cửa ghép song song - nối tiếp. 1 2G G G G1 G2 Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 30 Chương 7: Mạng hai cửa tuyến tính II.8. Các phương pháp tính bộ số đặc trưng. Để tính bộ số của mạng hai cửa tuyến tính không nguồn, ta có các cách sau: Dùng công thức định nghĩa. Lập phương trình mạch, biến đổi về dạng của phương trình bộ số cần tìm. Từ bộ số này tính ra bộ số khác. Phương pháp tổng hợp toán học. Ví dụ: Tính các bộ số của sơ đồ hình bên. 1I 2I 1U 2U ** M 1R 1L 2R 2L R Tính bộ Z. Lập phương trình dòng vòng 1 2 11 1 1 2 22 2 ( ). ( ). (1) ( ). ( ). (2) R R j L I R j M I U R j M I R R j L I U 1 1 2 2 R R j L R j M Z R j M R R j L Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 31 Chương 7: Mạng hai cửa tuyến tính II.8. Các phương pháp tính bộ số đặc trưng. Ví dụ: Tính các bộ số của sơ đồ hình bên. 1I 2I 1U 2U ** M 1R 1L 2R 2L R Tính bộ H. Từ phương trình (2): 212 12 22 22 1 . . Z I U I Z Z 12 21 12 11 22 22 21 22 22 . 1 Z Z Z Z Z Z H Z Z Z 11 211 12 2 1 221 22 . . . . U H I H U I H I H U 21 21 22 22 22 1 Z H Z H Z Thay vào phương trình (1): 12 21 12 12 1 1 11 2 211 21 11 22 22 22 . . . . . . Z Z Z Z U Z I U Z I Z I U Z Z Z 12 21 11 11 22 12 12 22 .Z Z H Z Z Z H Z Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 32 Chương 7: Mạng hai cửa tuyến tính II.8. Các phương pháp tính bộ số đặc trưng. Ví dụ: Tính các bộ số của sơ đồ hình bên. 1I 2I 1U 2U ** M 1R 1L 2R 2L R Tính bộ A. Từ phương trình (2): 221 22 21 21 1 . . Z I U I Z Z 11 11 22 12 21 21 22 21 21 . 1 Z Z Z Z Z Z A Z Z Z 21 211 12 1 2221 22 . . . . U A U A I I A U A I 21 21 22 22 21 1 A Z Z A Z Thay vào phương trình (1): 22 11 11 22 1 11 2 2 12 2 2 12 2 21 21 21 21 .1 . . . . . Z Z Z Z U Z U I Z I U Z I Z Z Z Z 11 11 21 11 22 12 12 21 . Z A Z Z Z A Z Z Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 33 CƠ SỞ KỸ THUẬT ĐIỆN 1 Chương 7: Mạng hai cửa tuyến tính I. Khái niệm về mạng hai cửa. II. Mô tả toán học của mạng hai cửa - Phương pháp tính các bộ số đặc trưng. III. Tính chất mạng 2 cửa tuyến tính tương hỗ. IV. Hàm truyền đạt dòng - áp. Tổng trở vào của mạng hai cửa. Vấn đề hòa hợp nguồn và tải bằng mạng hai cửa. V. Mạng hai cửa phi hỗ. VI. Khuếch đại thuật toán. Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 34 Chương 7: Mạng hai cửa tuyến tính III. Tính chất mạng 2 cửa tuyến tính tương hỗ. Nếu mạng 2 cửa là tuyến tính và tương hỗ thì: det 1 det 1 A B 12 21 12 21 Z Z Y Y 12 21 12 21 H H G G Nhận xét: Với mạng 2 cửa tuyến tính tương hỗ, ta luôn có 1 ràng buộc ở mỗi bộ số. Như vậy mạch chỉ còn 3 thông số độc lập tuyến tính Sơ đồ tương đương của mạng 2 cửa tuyến tính tương hỗ chỉ gồm 3 phần tử mắc theo sơ đồ hình T hoặc hình π Sơ đồ hình T Sơ đồ hình πZn2 Zd Zn1 Zn Zd2Zd1 tuyến tính tương hỗ 1I 1U 2I 2U Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 35 Chương 7: Mạng hai cửa tuyến tính III. Tính chất mạng 2 cửa tuyến tính tương hỗ. Mạng 2 cửa đối xứng là mạng 2 cửa mà khi ta thay đổi chiều truyền đạt trên các cửa 1 và 2, tính chất và phương trình truyền đạt vẫn không thay đổi. 11 22 11 22 A A B B 11 22 11 22 Z Z Y Y det H = 1 det G = 1 Nhận xét: Với mạng 2 cửa tuyến tính tương hỗ và đối xứng, chỉ có 2 thông số độc lập tuyến tính. E J Zt A, Z, G (B, Y, H) 21 Zt A, Z, G (B, Y, H) 21 E J A, Z, G (B, Y, H) 21 Mạng 2 cửa đối xứng Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 36 CƠ SỞ KỸ THUẬT ĐIỆN 1 Chương 7: Mạng hai cửa tuyến tính I. Khái niệm về mạng hai cửa. II. Mô tả toán học của mạng hai cửa - Phương pháp tính các bộ số đặc trưng. III. Tính chất mạng 2 cửa tuyến tính tương hỗ. IV. Hàm truyền đạt dòng - áp. Tổng trở vào của mạng hai cửa. Vấn đề hòa hợp nguồn và tải bằng mạng hai cửa. IV.1. Hàm truyền đạt dòng áp. IV.2. Tổng trở vào của mạng hai cửa. IV.3. Tổng trở vào ngăn mạch và hở mạch IV.4. Vấn đề hòa hợp nguồn và tải bằng mạng hai cửa. V. Mạng hai cửa phi hỗ. VI. Khuếch đại thuật toán. Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 37 Chương 7: Mạng hai cửa tuyến tính IV.1. Hàm truyền đạt dòng - áp. Trong những hệ truyền tin, đo lường, điều khiển ta chỉ quan tâm đến tín hiệu truyền đi thường là một trong hai biến trạng thái dòng, áp trên mỗi cửa và quá trình truyền đạt chúng qua mạng 2 cửa. Khi chỉ xét sự truyền đạt một tín hiệu dòng, áp như vậy không cần cả hệ 2 phương trình trạng thái với 4 hàm truyền đạt các dạng A, Z, G mà cần rút về một phương trình với một hàm truyền đạt. Ở đây ta chỉ xét đến hàm truyền đạt dòng, hàm truyền đạt áp và hàm truyền đạt công suất. Xét một mạng 2 cửa tuyến tính, không nguồn truyền đạt năng lượng tín hiệu đến một tải thụ động có hàm trở Z2. Ta viết một quan hệ tuyến tính đơn giản giữa tín hiệu cửa ra theo cửa vào dạng. 2 1 U U K U Nếu cần xét sự truyền đạt áp - áp trên 2 cửa, ta có hàm truyền đạt áp: Nếu cần xét sự truyền đạt dòng - dòng trên 2 cửa, ta có hàm truyền đạt áp: 2 1 I I K I Với mạch Kirchhoff ta quan tâm đến quan hệ công suất giữa 2 cửa: ~ 2 ~ 1 S S K S Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 38 Chương 7: Mạng hai cửa tuyến tính IV.2. Tổng trở vào của mạng 2 cửa. Khi xét quá trình năng lượng (tín hiệu đưa vào trên cửa 1 hoặc cửa 2) thực chất ta xét hệ mạng 2 cửa cùng với những bộ phận nó truyền đạt tới như là một mạng một cửa trong quan hệ trao đổi năng lượng tín hiệu với mạch ngoài. 1vZ Zt E J A, Z, G (B, Y, H) 1I 2I 1U 2U Quá trình trên cửa sẽ đặc trưng bởi một cặp biến dòng - áp, do đó sẽ đặc trưng bởi một hàm tổng trở vào hay tổng dẫn vào Zv (Yv). Khi mạng 2 cửa truyền đạt từ cửa 1 đến tải Zt ở cửa 2, quá trình năng lượng, tín hiệu ở cửa 1 đặc trưng bởi một hàm tổng trở vào cửa 1. 1 1 1 v U Z I Xét mối liên hệ giữa nguồn và tải ta nói rằng: Mạng 2 cửa đã làm một phép biến đổi tổng trở Zt thành Zv1. 211 2 12 2221 22 . . . . A U A I A U A I 22 .tU Z I 11 12 1 21 22 . . t v t A Z A Z A Z A Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 39 Chương 7: Mạng hai cửa tuyến tính IV.2. Tổng trở vào của mạng 2 cửa. Khi mạng 2 cửa truyền đạt từ cửa 2 đến tải Zt ở cửa 1, quá trình năng lượng, tín hiệu ở cửa 2 đặc trưng bởi một hàm tổng trở vào cửa 2. 2 2 2 ' 22 v U U Z II Zt A, Z, G (B, Y, H) E J 1I ' 22I I 1U 2U 2vZ Như vậy từ cửa 2, mạng 2 cửa cũng làm một phép biến đổi tổng trở Zt thành Zv2. 1122 12 121 1 11 . . . . A U A I A U A I 11 .tU Z I 22 12 2 21 11 . . t v t A Z A Z A Z A Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 40 Chương 7: Mạng hai cửa tuyến tính IV.3. Tổng trở vào ngắn mạch và hở mạch. E J A, Z, G (B, Y, H) 1I 2I 1U 2U Khi ngắn mạch hoặc hở mạch phía tải, trên cửa ra sẽ chỉ còn một tín hiệu điện áp hoặc dòng điện. Lúc đó tổng trở sẽ không tùy thuộc vào tải nữa mà là những hàm đặc trưng riêng của mạng 2 cửa. Xét cửa 2 hở mạch: 2 0I 211 2 12 11 1 212221 22 . . . . ho A U A I A Z AA U A I Xét cửa 2 ngắn mạch: 2 0U 211 2 12 12 1 222221 22 . . . . ng A U A I A Z AA U A I A, Z, G (B, Y, H) E J 1I ' 2I 1U 2U Xét cửa 1 hở mạch: 1 0I 122 1 12 22 2 211121 11 . . . . ho A U A I A Z AA U A I Xét cửa 1 ngắn mạch: 1 0U 122 1 12 12 2 111121 11 . . . . ng A U A I A Z AA U A I Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 41 Chương 7: Mạng hai cửa tuyến tính IV.3. Tổng trở vào ngắn mạch và hở mạch. Các hàm tổng trở Z1hở, Z1ng, Z2hở, Z2ng là 4 hàm đặc trưng của mạng 2 cửa, qua đó có thể tìm cách viết hệ phương trình trạng thái mạng 2 cửa hoặc tính ra các bộ số đặc trưng A, Z, G, của mạng 2 cửa. Ví dụ: Ta có thể tính bộ số A từ các giá trị của Z1hở, Z1ng, Z2ng theo công thức sau. 1 1 11 2 1 1 . .( ) ng ho ng ho ng Z Z A Z Z Z 12 11 2. ngA A Z 11 21 1ho A A Z 1222 1ng A A Z Trong thực tế thường sử dụng các công thức này vì một mạng 2 cửa chưa rõ kết cấu (hộp đen) thường có thể làm thí nghiệm ngắn mạch và hở mạch để đo các tổng trở vào, từ đó có thể tính bộ Aij hoặc các bộ số khác. Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 42 Chương 7: Mạng hai cửa tuyến tính IV.4. Vấn đề hòa hợp nguồn và tải bằng mạng 2 cửa. Như trong chương 6 đã đề cập, một nguồn có tổng trở Zng muốn truyền công suất lớn nhất đến tải Zt thì phải thỏa mãn điều kiện: ^ ng tZ Z Trong thực tế, nhiều khi Zng và Zt không thỏa mãn điều kiện hòa hợp. Zt Aij( )e t Zng 1vZ Cần chọn sơ đồ mạng 2 cửa và bộ số A sao cho: Tổng trở vào nhìn từ cửa 1 Zv1 bằng liên hiệp của tổng trở nguồn ^ ngZ Mạng 2 cửa A là thuần kháng để toàn bộ công suất từ nguồn truyền đến tải. ^ 11 12 1 21 22 . . t ngv t A Z A Z Z A Z A 2 4. ng ng E P R Nối thêm mạng 2 cửa để thực hiện phép biến đổi tổng trở vào. Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 43 CƠ SỞ KỸ THUẬT ĐIỆN 1 Chương 7: Mạng hai cửa tuyến tính I. Khái niệm về mạng hai cửa. II. Mô tả toán học của mạng hai cửa - Phương pháp tính các bộ số đặc trưng. III. Tính chất mạng 2 cửa tuyến tính tương hỗ. IV. Hàm truyền đạt dòng - áp. Tổng trở vào của mạng hai cửa. Vấn đề hòa hợp nguồn và tải bằng mạng hai cửa. V. Mạng hai cửa phi hỗ. V.1. Khái niệm. V.2. Các nguồn phụ thuộc. V.3. Sơ đồ tương đương của mạng hai cửa phi hỗ. VI. Khuếch đại thuật toán. Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 44 Chương 7: Mạng hai cửa tuyến tính V.1. Khái niệm. Mạng hai cửa phi hỗ là mạng hai cửa mà quan hệ các biến dòng, áp trên các cửa không có quan hệ tương hỗ với nhau. Khi đó các bộ số A, B, Z, Y, H, G có 4 tham số độc lập tuyến tính Mạch tương đương của mạng hai cửa phi hỗ ta có 4 phần tử. V.2. Các nguồn phụ thuộc. Nguồn phụ thuộc (nguồn bị điều khiển) là nguồn mà trạng thái dòng, áp của nó phụ thuộc vào trạng thái của một nhánh khác trong mạch. Phân loại: Nguồn áp phụ thuộc áp: Điện áp trên hai cực của nguồn phụ thuộc vào trạng thái điện áp trên một nhánh khác trong mạch. u1(t) e2(t) = k.u1(t) Nguồn áp phụ thuộc dòng: Điện áp trên hai cực của nguồn phụ thuộc vào trạng thái dòng điện trên một nhánh khác trong mạch. e2(t) = R.i1(t) i1(t) Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 45 Chương 7: Mạng hai cửa tuyến tính V.2. Các nguồn phụ thuộc. Phân loại: Nguồn dòng phụ thuộc áp: Dòng điện sinh ra bởi nguồn phụ thuộc vào trạng thái điện áp trên một nhánh khác trong mạch. Nguồn dòng phụ thuộc dòng: Dòng điện của nguồn phụ thuộc vào trạng thái dòng điện trên một nhánh khác trong mạch. u1(t) j2(t) = Y.u1(t) j2(t) = α.i1(t) i1(t) Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 46 Chương 7: Mạng hai cửa tuyến tính V.3. Sơ đồ tương đương của mạng hai cửa phi hỗ. Do mạng hai cửa phi hỗ có 4 tham số độc lập tuyến tính nên sơ đồ tương đương của mạng 2 cửa phi hỗ sẽ bao gồm 4 phần tử. Xét bộ Z: Sơ đồ tương đương dùng 2 trở kháng + 2 nguồn bị điều khiển. 1 11 1 12 2 2 21 1 22 2 . . . . u Z i Z i u Z i Z i u1(t) i1(t) Z11 e1= Z12.i2 e2= Z21.i1 i2(t) Z22 u2(t) Xét bộ Y: 1 11 1 12 2 2 21 1 22 2 . . . . i Y u Y u i Y u Y u j1= Y12.u2 i1(t) Y11 u1(t) j1 Y22 u2(t)j2 i2(t) j2= Y21.u1 Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 47 Chương 7: Mạng hai cửa tuyến tính V.3. Sơ đồ tương đương của mạng hai cửa phi hỗ. Sơ đồ dùng 2 trở kháng + 2 nguồn bị điều khiển. Xét bộ H: 1 11 1 12 2 2 21 1 22 2 . . . . u H i H u i H i H u Xét bộ G: 1 11 1 12 2 2 21 1 22 2 . . . . i G u G i u G u G i H22 u2(t)j2 i2(t) j2= H21.i1 u1(t) i1(t) H11 e1= H12.u2 e1 j1= G12.i2 i1(t) G11 u1(t) j1 e2 i2(t) G22 u2(t) e2= G21.u1 Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 48 Chương 7: Mạng hai cửa tuyến tính V.3. Sơ đồ tương đương của mạng hai cửa phi hỗ. Sơ đồ tương đương dùng 3 trở kháng + 1 nguồn bị điều khiển. Xét bộ Z: 1 11 1 12 2 2 21 1 22 2 . . . . u Z i Z i u Z i Z i 21 12 ZZ Z 1 11 1 12 2 2 12 1 22 2 . . . . u Z i Z i u Z i Z i 1.Z i Sơ đồ hình T u1(t) i2(t) Zd1 Zd2 Zn i1(t) u2(t)1 .e Z i Với bộ Z đã cho, ta luôn tính được các giá trị Zd1, Zd2, và Zn theo công thức: 12 2 22 12 1 11 12 21 12 n d d Z Z Z Z Z Z Z Z Z Z Z Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 49 Chương 7: Mạng hai cửa tuyến tính V.3. Sơ đồ tương đương của mạng hai cửa phi hỗ. Sơ đồ tương đương dùng 3 trở kháng + 1 nguồn bị điều khiển. Xét bộ Y: 1 11 1 12 2 2 21 1 22 2 . . . . i Y u Y u i Y u Y u 21 12 YY Y 1 11 1 12 2 2 12 1 22 2 . . . . i Y u Y u i Y u Y u 1.Y u Sơ đồ hình π Với bộ Y đã cho, ta luôn tính được các giá trị Yn1, Yn2, và Yd theo công thức: 12 2 22 12 1 11 12 21 12 1 Y Y ( ) . ( ) d n n Y Y Y Y Y Y Y Y Y j t Y u t i1(t) Yn1u1(t) Yn2 u2(t) Yd i2(t) ( )j t Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chương 7: Mạng hai cửa tuyến tính VI. Khuếch đại thuật toán 1. Khái niệm 50 + - P N Khuếch đại thuật toán là một phần tử phức hợp của mạch điện, có 2 cửa ngõ. Các thông số của OPAM lý tưởng : Rvào = ∞ ; IN = 0 ; Rra = 0 ; IP = 0 ; Hệ số khuếch đại trong (μ = ∞) Ví dụ : Khuếch đại thuật toán μA741 Rvào = 2MΩ Rra = 50Ω μ = 200000 Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chương 7: Mạng hai cửa tuyến tính 51 VI. Khuếch đại thuật toán 2. Sơ đồ thay thế. V + Rvào μ.(V + - V -) V - Rra ura(t) V + Rvào μ.(V + - V -) V - Rra ura(t) Rvào + - Sơ đồ đầu vào so đất + - Sơ đồ vi sai
File đính kèm:
 bai_giang_ky_thuat_dien_1_chuong_7_mang_hai_cua_tuyen_tinh_n.pdf
bai_giang_ky_thuat_dien_1_chuong_7_mang_hai_cua_tuyen_tinh_n.pdf

