Bài giảng Kỹ thuật điện 1 - Chương 10: Các phương pháp tính quá trình quá độ trong mạch điện tuyến tính - Nguyễn Việt Sơn
Ý nghĩa:
Nghiệm xác lập xxl(t):
Về mặt toán học:
o Nghiệm xác lập là nghiệm riêng của phương trình vi phân có vế phải là kích thích
của mạch ta đã biết cách tính nghiệm xác lập khi kích thích của mạch là nguồn
hằng, nguồn điều hòa, hay nguồn chu kỳ.
Nghiệm tự do xtd(t):
Về mặt vật lý:
o Nghiệm tự do không được nguồn duy trì.
o Nghiệm tự do tồn tại trong mạch là do quá trình đóng cắt khóa K làm thay đổi kết
cấu hay thông số của mạch.
Về mặt toán học:
Nghiệm tự do là nghiệm riêng của phương trình vi phân thuần nhất (phương trình vi
phân có vế phải bằng 0)

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
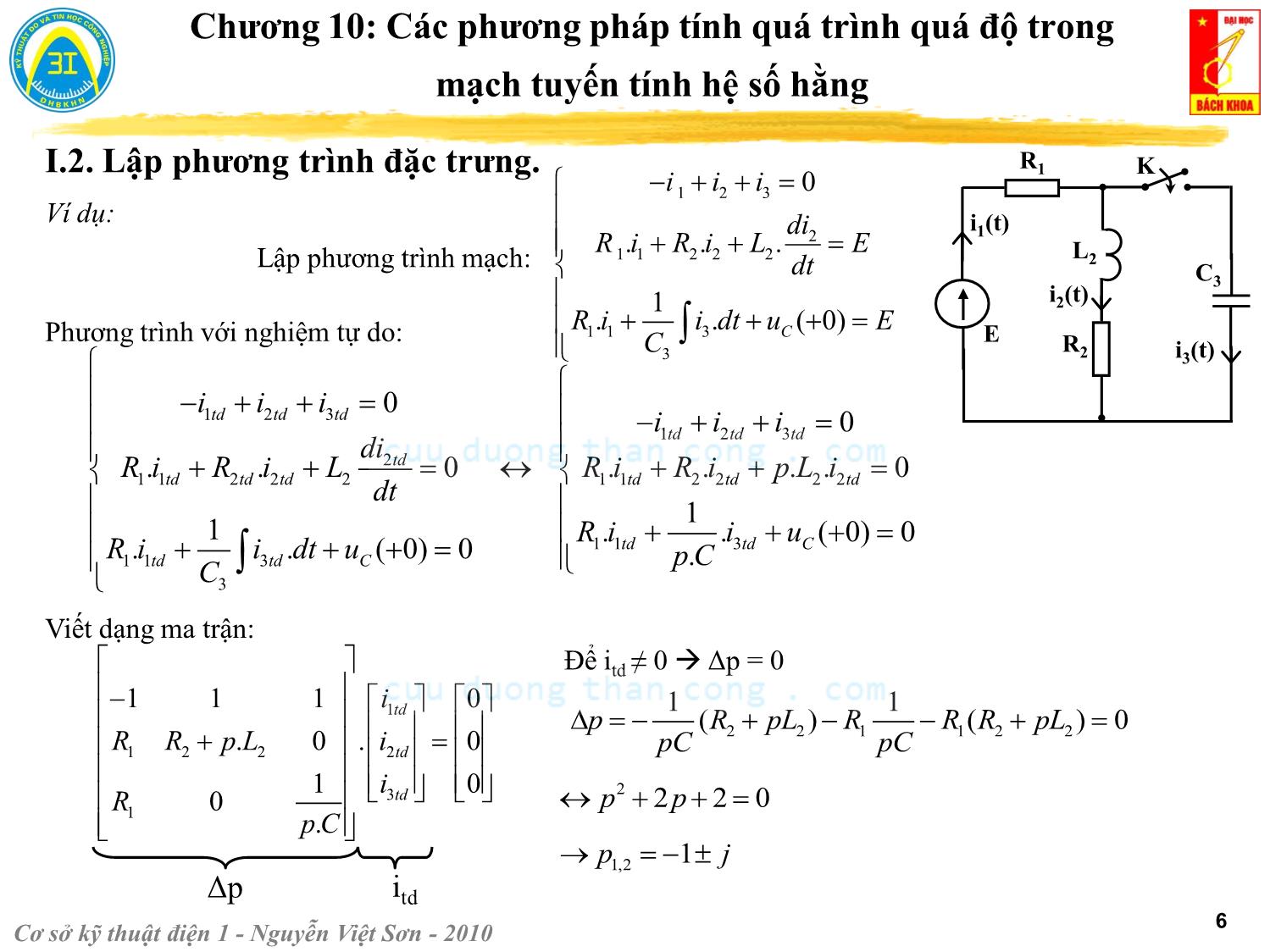
Trang 6

Trang 7
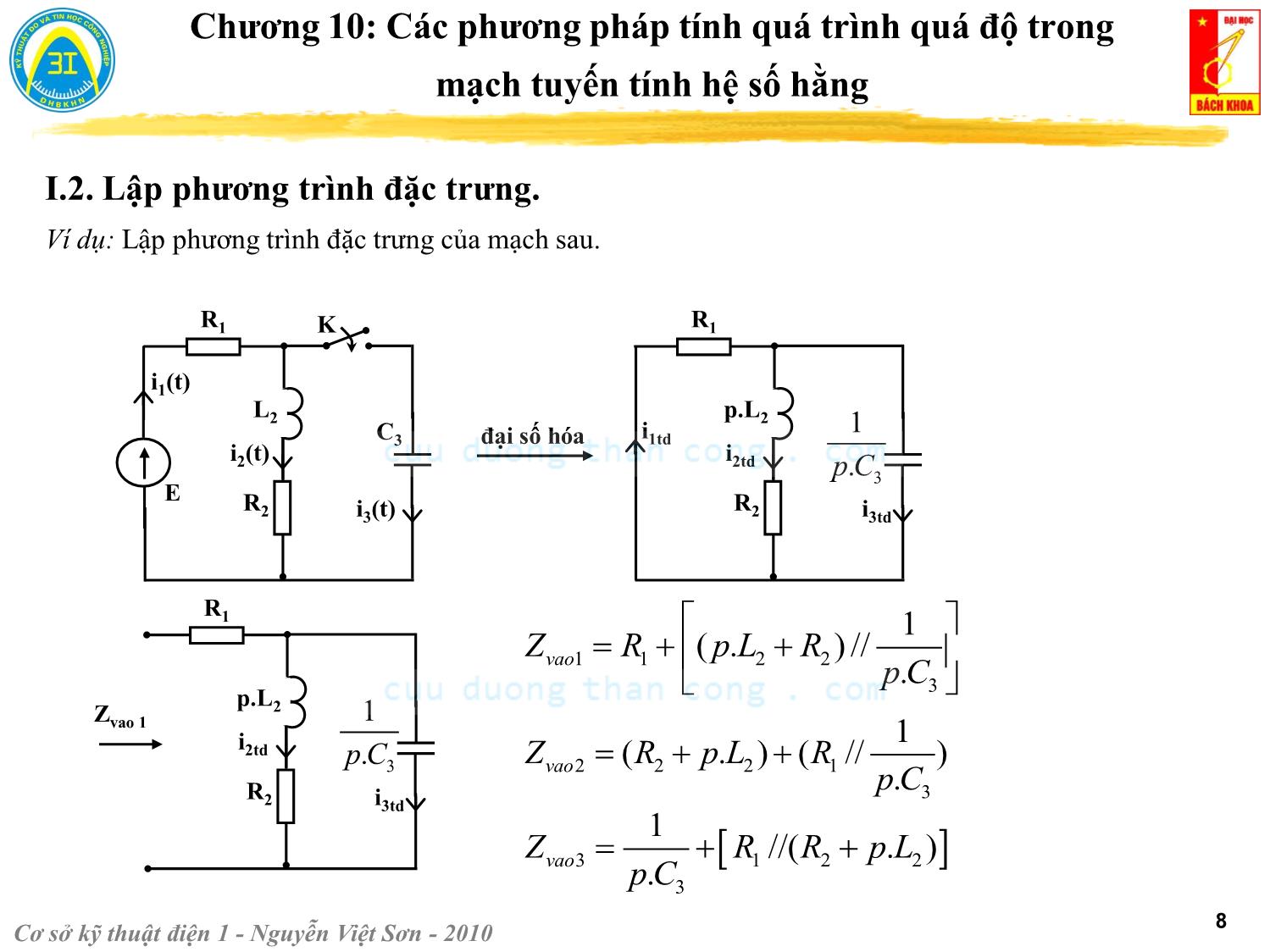
Trang 8
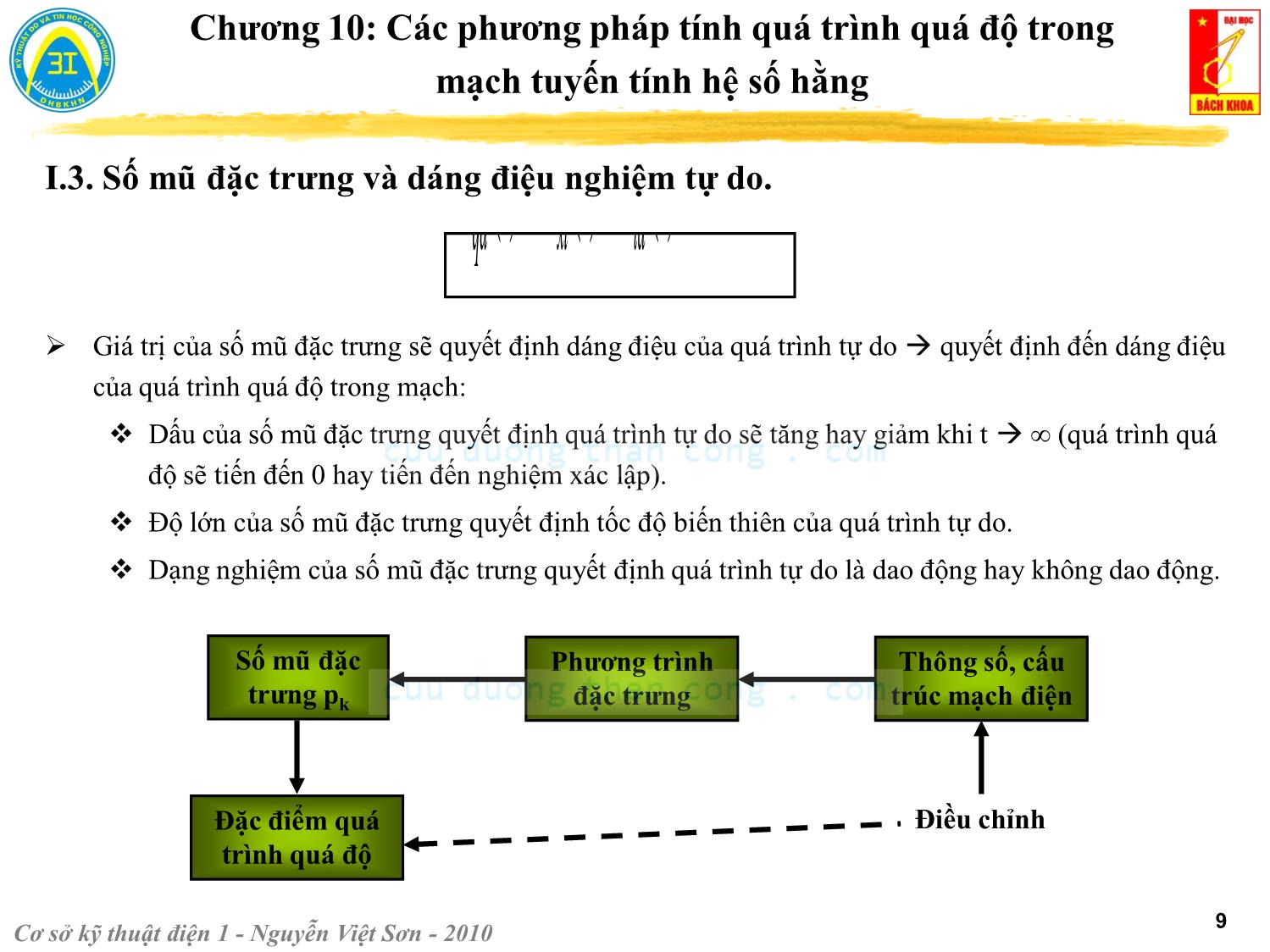
Trang 9
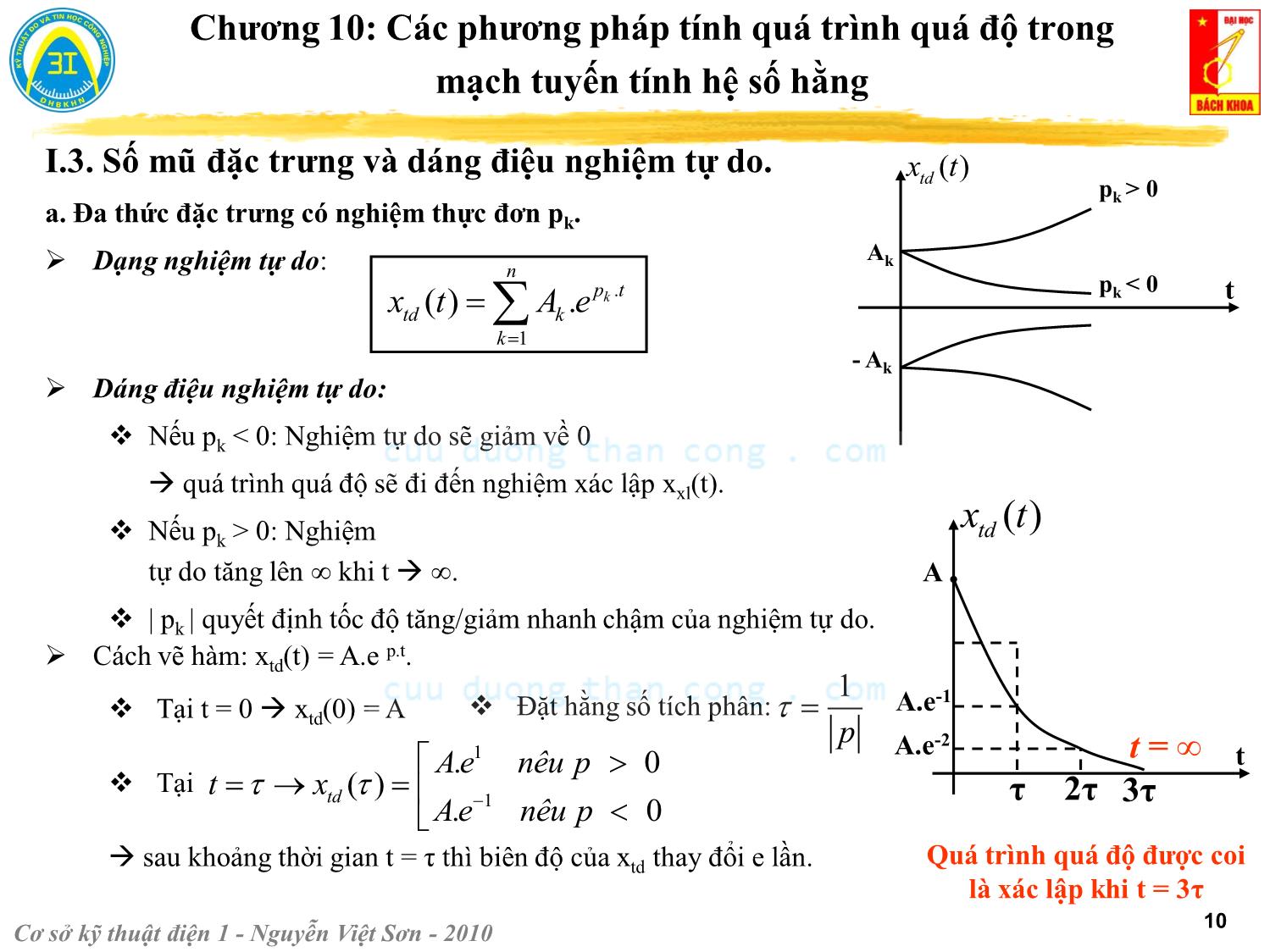
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kỹ thuật điện 1 - Chương 10: Các phương pháp tính quá trình quá độ trong mạch điện tuyến tính - Nguyễn Việt Sơn", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật điện 1 - Chương 10: Các phương pháp tính quá trình quá độ trong mạch điện tuyến tính - Nguyễn Việt Sơn

ch xung Dirac t δ(t- τ) τ Mạch tuyến tính Đáp ứngKích thích g(t- τ) Kích thích nguyên tố t f(τ ).δ(t- τ).d(τ) dτ dx(t) = f(τ).dτ.g(t- τ) Kích thích 1(t).f(t) t 1(t).f(t ) 0 1.( ). ( ) ( ). ( ). * t t x t f g t d f g 0 1( ). ( ) * ( ). ( ). t t x t g f g f t d Tính giao hoán Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng II.2. Phƣơng pháp hàm Green. b. Đáp ứng hàm Green g(t). 36 Nhận xét: Việc sử dụng và tính toán với hàm Green sẽ ngắn gọn hơn do không có các số hạng liên quan đến bước nhảy của kích thích và hàm truyền đạt: f(0).h(t), h(0).f(t) ' 0 1( ). ( ) 1( ). (0). ( ) ( ). ( ). t t x t t f h t f h t d ' 0 1( ). ( ) (0). ( ) ( ). ( ). t t x t h f t f h t d Công thức Duyamen 0 ( ) ( ). ( ). t x t f g t d 0 ( ) ( ). ( ). t x t g f t d Hàm Green Công thức hàm Green dùng chung cho mọi quãng thời gian t mà không cần chú ý tới những đoạn chắp nối của hàm φ(t) Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng II.2. Phƣơng pháp hàm Green. c. Cách tìm hàm Green g(t). 37 So sánh công thức hàm Green và công thức tích phân Duyamen nghĩa rộng, ta có: 0 ( ) ( ). ( ). t x t f g t d 0 ( ) ( ). ( ). t x t g f t d Hàm Green ' 0 1( ). ( ) ( ). ( ). t t x t h t d ' 0 1( ). ( ) ( ). ( ). t t x t h t d Công thức Duyamen ( ) ( ) ( ) dh t dh t g t d dt ( ) ( ) d g t h t dt Suy ra: Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng II.2. Phƣơng pháp hàm Green. c. Cách tìm hàm Green g(t). 38 Ví dụ 1: Tính áp uC(t) quá độ trong mạch R - C khi tác động là xung áp như hình vẽ. e(t) K R C t T e(t) U 0 Ta có: ( ) .[1( ) 1( )]e t U t t T .( ) 1 C t uh t e 1 .R C với t .( ) 0 1( ). ( ) * . . .[1( ) 1( )].d C t C ut u t u g e U T Biết đáp ứng Hevixaid với áp trên tụ: Vậy hàm Green tương ứng: ' .( ) ( ) . C C t u ug t h t e Áp quá độ trên tụ là: .( ) .( ) 0 0 1( ). ( ) . .1( ). . .1( ). t t t t Ct u t U e d U e t d .( ) ( ) . .( ) 0 0 1( ). ( ) . 1( ). . . 1 1( ). 1 t t t t t t T Ct u t U e t U e U e t T U e Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng II.2. Phƣơng pháp hàm Green. c. Cách tìm hàm Green g(t). 39 Ví dụ 2: Tính áp quá độ uC(t), uR(t) trong mạch R - C khi tác động là xung áp hàm mũ e(t) K R C t e(t) 0 .. tU e Đáp ứng Hevixaid của các áp uC(t), uR(t) trong mạch R-C có dạng: . 1( ) 1( ). , ( ) 1 , .R C t t u uh t t e h t e R C Vậy các hàm Green tương ứng là: Áp quá độ trên R là: ( ) ( ) .1( ). R t ug t t t e ( ) . C t ug t e 1 . .( ) .( ) . ( ). . . 0 0 1( ). ( ) ( ) . . . . . . . . t t t t t t R U t u t U t e e d U e e e e e Áp quá độ trên C là: . ( ) . ( ). . . 0 0 1( ). ( ) . . . . . . . tt t t t t Ct u t U e e d U e e U e e Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 40 CƠ SỞ KỸ THUẬT ĐIỆN 1 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng. I. Phƣơng pháp tích phân kinh điển. II. Phƣơng pháp tích phân Duyamen và hàm Green. III. Phƣơng pháp toán tử Laplace. III.1. Tinh thần của phƣơng pháp toán tử Laplace. III.2. Các định lý về quan hệ ảnh - gốc. III.3. Cách tìm gốc theo ảnh Laplace. III.4. Tính quá trình quá độ bằng phƣơng pháp toán tử Laplace. Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.1. Tinh thần của phƣơng pháp toán tử Laplace. Làm phép song ánh biến đổi cặp “phân bố thời gian φ(t) = 1(t).f(t) (hàm gốc thời gian) và số phức p” với một số phức F(p) (ảnh Laplace) sao cho: 41 t ( ).t dt p.F(p) 1 . ( )F p p Hệ phƣơng trình vi tích phân hệ số hằng Hệ phƣơng trình đại số tuyến tính ảnh F(p) Nhờ quan hệ song ánh đó: Giải phương trình đại số tìm ảnh F(p) tìm được nghiệm gốc φ(t). Xét tính chất về đại số của ảnh F(p) khảo sát được dáng điệu nghiệm của phương trình vi tích phân. Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.2. Các định lý về quan hệ ảnh - gốc. 42 a. Đạo hàm gốc. Xét hàm f(t) bất kỳ. 1(t).f(t) F(p) Đạo hàm của f(t): ' 1( ). ( ) 1( ). '( ) ( ). (0)t f t t f t t f ' 1( ). '( ) 1( ). ( ) ( ). (0)t f t t f t t f 1( ). '( ) . ( ) ( 0)t f t p F p f Tại t = 0: ( 0) ( 0)f f f 1( ). '( ) . ( ) ( 0) [ ( 0) ( 0)]t f t p F p f f f 1( ). '( ) . ( ) ( 0)t f t p F p f t f(t) -0 +0 ( 0) ( 0)f f f Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.2. Các định lý về quan hệ ảnh - gốc. 43 a. Đạo hàm gốc. Ứng dụng: Xét cuộn dây: '( ) . ( ) . ( )L d u t L i t L i t dt i(t) L u(t) Chuyển sang miền ảnh: iL(t) IL (p) uL(t) UL (p) I(p) p.L U(p) L.i(-0) ( )( 0) ( ) . L L U pi I p p p L ( ) .[ . ( ) ( 0)]L LU p L p I p i ( ) . . ( ) . ( 0)]L LU p p L I p L i U(p) I(p) 1 .p L ( 0)Li p Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.2. Các định lý về quan hệ ảnh - gốc. 44 b. Tích phân gốc. Xét hàm f(t) bất kỳ. 1(t).f(t) F(p) Tích phân của f(t): 0 1( ). ( ). t t f t dt 1 . ( )F p p Ứng dụng: Xét tụ điện. 1 ( ) (0) . ( ).C Cu t u i t dt C Chuyển sang miền ảnh. CiC(t) uC(t) iC(t) IC(p) uC(t) ( 0)1 ( ) . ( ) . C C C u U p I p p C p IC(p) UC(p) 1 .p C ( 0)Cu p I(p) p.C C.uC(-0) UC(p) UC(p) ( ) . . ( ) . ( 0)C C CI p p CU p C u Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.2. Các định lý về quan hệ ảnh - gốc. 45 b. Định lý về dịch gốc. Xét hàm f(t) bất kỳ. Vậy: 1( ). ( )t f t ( )F p 1( ). ( )t T f t T . . ( )T pe F p Ví dụ: t 0.2 e(t) 10 0 1( ). ( ) 10.1( ) 10.1( 0.2)t e t t t 0.2 0.210 10 10. .(1 )p pe e p p p Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.2. Các định lý về quan hệ ảnh - gốc. 46 c. Định lý về dịch ảnh. Xét hàm f(t) bất kỳ. Vậy: 1( ). ( )t f t ( )F p .1( ). ( ). a tt f t e ( )F p a d. Định lý về sự đồng dạng. Xét hàm f(t) bất kỳ. Vậy: 1( ). ( )t f t ( )F p 1( ). ( . )t f a t 1 . ( ) p F a a 1( ). ( ) t t f a . ( . )a F a p e. Đạo hàm ảnh. Xét hàm f(t) bất kỳ. Vậy: 1( ). ( )t f t ( )F p 1( ).( ). ( )t t f t ( ) d F p dp Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.2. Các định lý về quan hệ ảnh - gốc. 47 f. Tích phân ảnh. Xét hàm f(t) bất kỳ. Vậy: 1( ). ( )t f t ( )F p 1 1( ). ( )t f t t 0 ( ). p F p dp g. Định lý tích xếp. Xét hàm f(t) bất kỳ. Vậy: 1( ). ( )t f t ( )F p 1 2 0 ( ). ( ). t f f t d 1 2( ). ( )F p F p g. Định lý về các giá trị bờ. Xét hàm f(t) bất kỳ. 1( ). ( )t f t ( )F p Vậy: 0 lim1( ). ( ) t t f t lim . ( ) p p F p lim1( ). ( ) t t f t 0 lim . ( ) p p F p Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.3. Cách tìm gốc theo ảnh Laplace. 48 a. Phép tích phân Riman-Mellin. .11( ). ( ) ( ). . 2. . a j t p a j t f t F p e dp j b. Tra bảng quan hệ ảnh - gốc. 1 1( )t p 2 1 t p ( ) 1t . 1a te p a 2 2 cos( . ) p a t p a 2 2 sin( . ) a a t p a Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.3. Cách tìm gốc theo ảnh Laplace. 49 c. Dùng công thức Hevixaide Khi xét mạch, ta thường gặp phân thức hữu tỉ dạng: 2 0 1 2 1 2 0 1 2 2 . . ... . ( ) ( ) . . ... . ( ) m m n n b b p b p b p F p F p a a p a p a p F p a0 an, b0 bm: hằng số thực Công thức Hevixaide cho gốc của ảnh Laplace F(p) khi đa thức tử số F1(p) có bậc nhỏ hơn đa thức mẫu số F2(p) (m < n) (trong trường hợp m ≥ n, ta sẽ thực hiện phép chia đa thức). Nếu F2(p) = 0 có nghiệm thực, đơn: p1, p2. 1 2. . 1 21( ). ( ) . . p t p t t f t A e A e 1 ' 2 ( ) lim ( )k k p p F p A F p với (k = 1,2) Nếu F2(p) = 0 có nghiệm thực kép: p1 = p2 = pk. . 1 21( ). ( ) ( . ). p tt f t A A t e 21 1 2 ( ) lim .( ) ( )k k p p F pd A p p dp F p với 21 2 2 ( ) lim .( ) ( )k k p p F p A p p F p Nếu F2(p) = 0 có phức: p1,2 = - α ± j.β .1( ). ( ) 2. . .cos( . )tk kt f t A e t với . 1 ' 2 ( ) lim ( )k k k k p p F p A A F p Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.3. Cách tìm gốc theo ảnh Laplace. 50 c. Dùng công thức Hevixaide Ví dụ: Tìm hàm gốc của các ảnh sau. 1 2 ( )20 ( ) ( 5).( 6) ( ) F p I p p p F p 5. 6. 1 21( ). ( ) . . t tt i t A e A e 1 2 2 5 ( ) 0 6 p F p p ' 2 ( ) 2 11F p p 1 5 20 lim 20 2. 11p A p 2 6 20 lim 20 2. 11p A p 5. 6.1( ). ( ) 20 ) .( t tt i t e e 2 1 2 2 ( )2 ( ) .( 4) ( ) F pp E p p p F p 4. 0 1 2 1( ). ( ) ( . ). tt e t A A A t e 1 2 2 3 0 ( ) 0 4 p F p p p ' 2 2 ( ) 3. 16. 16F p p p 1 0 '0 2 ( ) 1 lim ( ) 8p F p A F p 21 1 4 2 ( ) 7 lim .( 4) ( ) 8p F pd A p dp F p 4.1 7 91( ). ( ) . . 8 8 2 tt e t t e 21 2 4 2 ( ) 9 lim .( 4) ( ) 2p F p A p F p Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.3. Cách tìm gốc theo ảnh Laplace. 51 c. Dùng công thức Hevixaide Ví dụ: Tìm hàm gốc của các ảnh sau. 1 2 2 ( )100 ( ) 2. 10 ( ) F p U p p p F p 1( ). ( ) 2. . .cos(3. )tt u t A e t 2 1,2( ) 0 1 .3F p p j . 0 1 .3 100 100 100 lim 90 2.( 1) .6 6p j A p j 1( ). ( ) 33.333. .co s(3. ) 2 tt u t e t ' 2 ( ) 2. 2F p p Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.4. Tính quá trình quá độ bằng phƣơng pháp toán tử Laplace. 52 a. Sơ đồ toán tử. Sơ đồ toán tử là sơ đồ mạch ở chế độ mới trong đó các kích thích j(t), e(t) đã được chuyển sang miền ảnh J(p), E(p); các phần tử R, L, C được chuyển sang miền ảnh kèm theo sơ kiện. Kích thích của mạch: e(t) j(t) E(p) J(p) Các phần tử iL(t) L uL(t) IL(p) p.L UL(p) L.i(-0) CiC(t) uC(t) IC(p) UC(p) 1 .p C ( 0)Cu p p.C I(p) C.uC(-0) UC(p) RiR(t) uR(t) RIR(p) UR(p) ( )( 0) ( ) . L L U pi I p p p L ( ) . . ( ) . ( 0)]L LU p p L I p L i IL(p) 1 .p L ( 0)Li p UL(p) ( 0)1 ( ) . ( ) . C C C u U p I p p C p ( ) . . ( ) . ( 0)C C CI p p CU p C u ( ) . ( )R RU p R I p Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.4. Tính quá trình quá độ bằng phƣơng pháp toán tử Laplace. 53 b. Các luật trong miền ảnh Laplace. Luật Ohm: ( ) . ( ) ( ) . ( ) U p Z I p I p Y U p Luật Kirchhoff 1: ( ) 0 nut I p Luật Kirchhoff 2: ( ) ( ) vong vong U p E p (có tính đến sơ kiện) Hệ phƣơng trình vi tích phân + sơ kiện Hệ phƣơng trình đại số ảnh Laplace + sơ kiện Miền thời gian Miền ảnh Laplace Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.4. Tính quá trình quá độ bằng phƣơng pháp toán tử Laplace. 54 c. Trình tự giải bài toán quá trình quá độ. Tìm sơ kiện độc lập của mạch tại t = -0: uC(-0) ; iL(-0) Lập sơ đồ toán tử cho mạch điện ở chế độ mới. Lập và giải phương trình mạch trong miền ảnh Laplace để tìm nghiệm X(p) Tìm nghiệm quá độ xqd(t). Xét mạch ở chế độ cũ và tính các đáp ứng uC(t), iL(t) Thay tại t = -0 để tính các sơ kiện độc lập uC(-0), iL(-0) Lập phương trình mạch theo phương pháp: Dòng nhánh, dòng vòng, thế đỉnh, mạng 1 cửa, 2 cửa Tra bảng quan hệ ảnh - gốc. Dùng công thức Hevixaide. Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.4. Tính quá trình quá độ bằng phƣơng pháp toán tử Laplace. 55 c. Trình tự giải bài toán quá trình quá độ. Ví dụ: Tìm iCqd(t) khi đóng mạch từ vị trí 1 sang vị trí 2, biết: e1(t) R1 C R221 e2(t) 3 20. 1 2( ) 100.sin10 . ( ) ; ( ) 100. ( ) te t t V e t e V 1 210 ; 100 ; 10CR R X Giải: Tìm sơ kiện độc lập uC(-0): . . 1max 0 1 1 100 . 45 1 . . 2 . . C E U j C R j C 3 0100( ) sin(10 . 45 ) 2 Cu t t ( 0) 50( ) Cu V Lập sơ đồ toán tử: R2 E2(p)1 .p C ( 0)Cu p 2 1 2 ( 0) ( ) ( )1,5. 10 ( ) 1 ( 20)( 100) ( ) . CuE p F ppp I p p p F p R p C 20. 100. 1 21( ). ( ) . . t t Cqdt i t A e A e 1 1 '20 2 ( ) lim 0,25 ( )p F p A F p 1 2 '100 2 ( ) lim 1,75 ( )p F p A F p 20. 100.1( ). ( ) 0,25. 1,7 5.t tCqdt i t e e Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.4. Tính quá trình quá độ bằng phƣơng pháp toán tử Laplace. 56 c. Trình tự giải bài toán quá trình quá độ. Ví dụ: Tính dòng quá độ trong mạch, biết: E = 10 V = const ; R1 = 5Ω; R3 = R2 = 10Ω; L1 = 2H; L2 = 2H; M=1H. Giải: E R1 R3 * L1 K * R2 L2 * p.L1 R2 * p.L2 -2.p.M M.i2(-0) L1.i1(-0) M.i1(-0) L2.i2(-0) Tìm sơ kiện độc lập: 1 1 2 3 10 ( 0) 1( ) ( // ) 5 5 E i A R R R 1 2 ( 0) ( 0) 0.5( ) 2 i i A Lập sơ đồ toán tử: R1 10 p 1 1 2 2 2 1 1 2 1 2 ( ) . ( 0) . ( 0) . ( 0) . ( 0) ( ) . . 2. . E p L i M i L i M i I p R R p L p L p M I(p) i2i1 0.75. 5 ( ) .( 7.5) p I p p p 7,5.1( ). ( ) 0,667 0,0833. ( )tt i t e A Cơ sở kỹ thuật điện 1 - Nguyễn Việt Sơn - 2010 Chƣơng 10: Các phƣơng pháp tính quá trình quá độ trong mạch tuyến tính hệ số hằng III.4. Tính quá trình quá độ bằng phƣơng pháp toán tử Laplace. 57 d. Nhận xét chung về phƣơng pháp. Ƣu điểm: Nhƣợc điểm: Giải bài toán quá trình quá độ với nguồn kích thích bất kỳ (tăng không nhanh hơn hàm e mũ) Chỉ cần tính sơ kiện độc lập tại t = - 0. Giải được trực tiếp nghiệm quá độ. Có thể thay thế được cho mọi phương pháp tích phân. Khi F2(p) là đa thức bậc cao, ta phải dùng phương pháp gần đúng để tìm nghiệm pk.
File đính kèm:
 bai_giang_ky_thuat_dien_1_chuong_10_cac_phuong_phap_tinh_qua.pdf
bai_giang_ky_thuat_dien_1_chuong_10_cac_phuong_phap_tinh_qua.pdf

