Bài giảng Kỹ thuật cao áp - Chương 8: Xử lý dữ liệu điện áp đánh thủng
1. Giới thiệu
Nếu tăng điện áp tác dụng giữa hai điện cực một cách từ từ
cuối cùng sẽ dẫn đến phóng điện tại điện áp đánh thủng
Lặp lại thí nghiệm trong cùng điều kiện sẽ thu được giá trị điện áp
phóng điện khác so với giá trị ban đầu kết quả thí nghiệm
không tái sản xuất được
Độ bền điện quan sát thay đổi theo từng thí nghiệm có nghĩa là
thay đổi một cách ngẫu nhiên các phương pháp thống kê được
sử dụng để mô tả và dự đoán gần đúng giá trị độ bền điện hoặc
điện áp phóng điện2. Hàm phân phối xác suất
Từ thí nghiệm thu được tập hợp số liệu điện áp phóng điện, theo
kinh nghiệm, có thể xác định được hàm phân phối tích lũy của các
giá trị điện áp phóng điện.
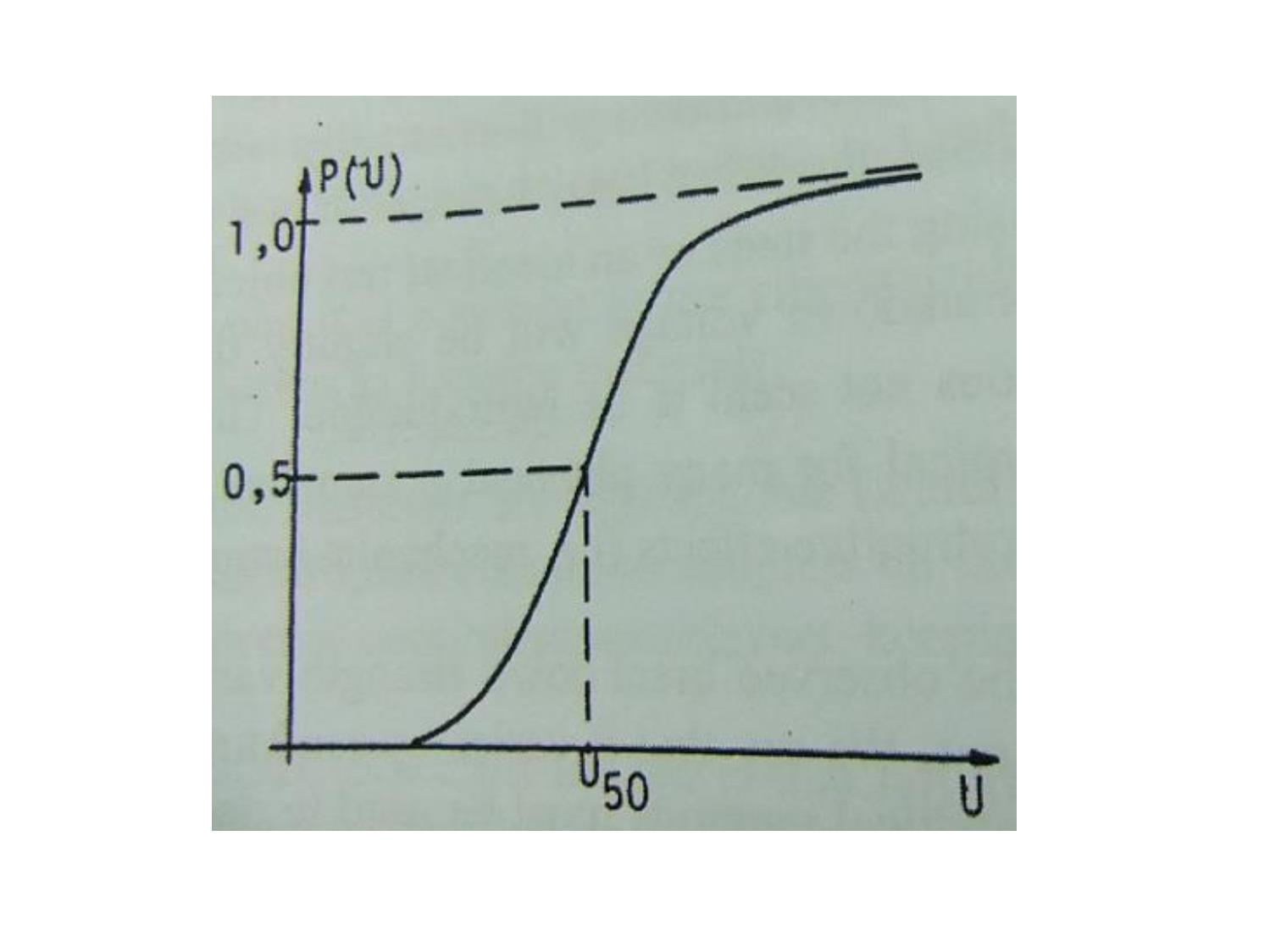
Hàm phân phối này mô tả xác suất tích lũy xảy ra phóng điện tại
giá trị điện áp ngẫu nhiên nhỏ hơn hoặc bằng U
Xác suất xảy ra phóng điện được xác định như sau:
Với: n là tổng số lần thử nghiệm và no là số lần xảy ra phóng điện
tại các giá trị điện áp nhỏ hơn hay bằng U

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5
Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Kỹ thuật cao áp - Chương 8: Xử lý dữ liệu điện áp đánh thủng

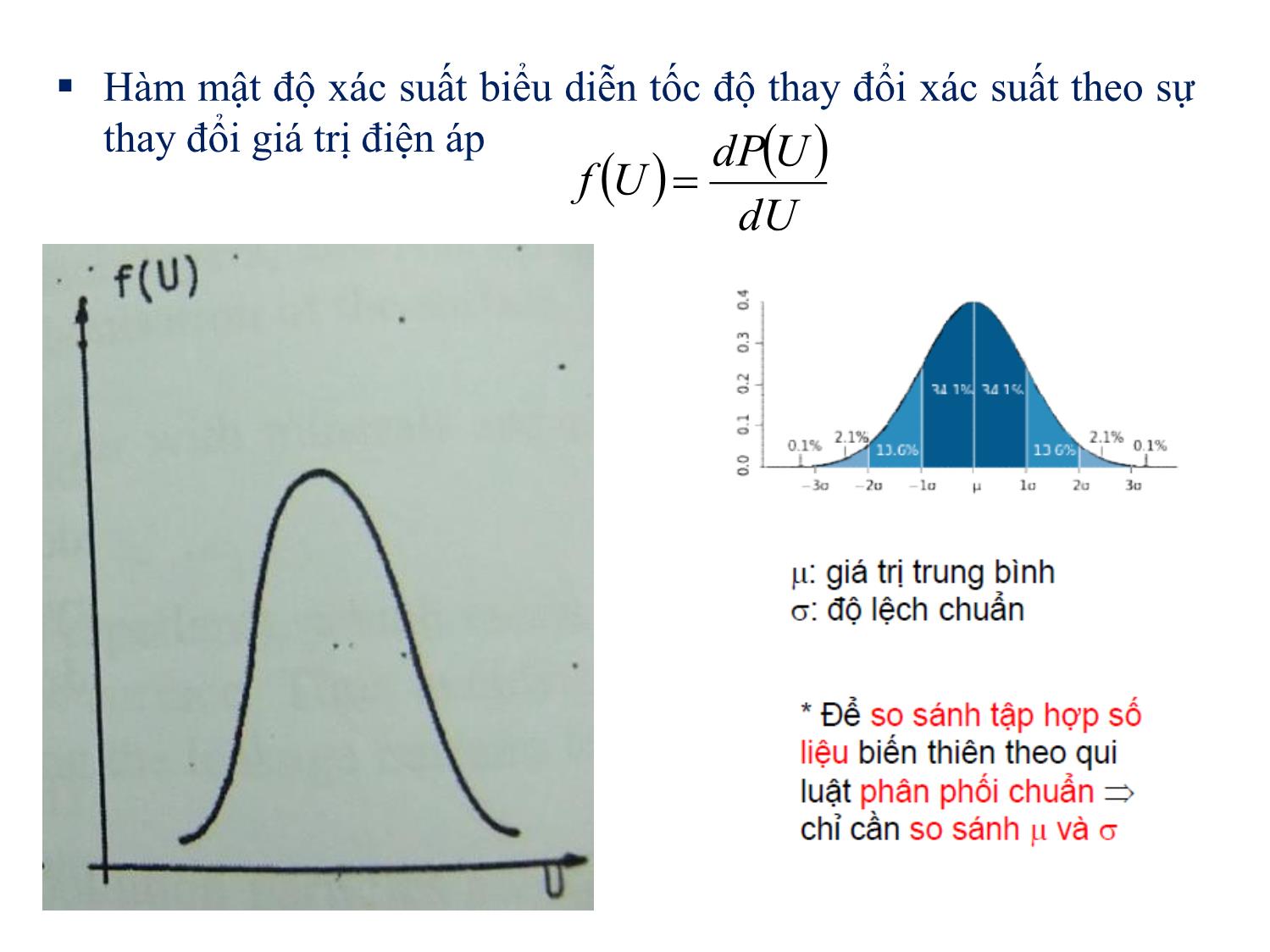
CHƯƠNG VIII: XỬ LÝ DỮ LIỆU ĐIỆN ÁP ĐÁNH THỦNG 1. Giới thiệu 2. Hàm phân phối xác suất 3. Ảnh hưởng của diện tích bề mặt điện cực và thể tích của vật liệu cách điện 4. Cách sử dụng giấy Weibull 1. Giới thiệu Nếu tăng điện áp tác dụng giữa hai điện cực một cách từ từ cuối cùng sẽ dẫn đến phóng điện tại điện áp đánh thủng Lặp lại thí nghiệm trong cùng điều kiện sẽ thu được giá trị điện áp phóng điện khác so với giá trị ban đầu kết quả thí nghiệm không tái sản xuất được Độ bền điện quan sát thay đổi theo từng thí nghiệm có nghĩa là thay đổi một cách ngẫu nhiên các phương pháp thống kê được sử dụng để mô tả và dự đoán gần đúng giá trị độ bền điện hoặc điện áp phóng điện 2. Hàm phân phối xác suất Từ thí nghiệm thu được tập hợp số liệu điện áp phóng điện, theo kinh nghiệm, có thể xác định được hàm phân phối tích lũy của các giá trị điện áp phóng điện. Hàm phân phối này mô tả xác suất tích lũy xảy ra phóng điện tại giá trị điện áp ngẫu nhiên nhỏ hơn hoặc bằng U Xác suất xảy ra phóng điện được xác định như sau: nkhi n n UP olim Với: n là tổng số lần thử nghiệm và no là số lần xảy ra phóng điện tại các giá trị điện áp nhỏ hơn hay bằng U Thực tế, không thể xác định chính xác giá trị P(U) vì số lần thử nghiệm hạn chế chỉ ước lượng P(U) từ số lần thí nghiệm cụ thể Từ lý thuyết thống kê, ước lượng phù hợp nhất khi biểu diễn đồ thị P = f(U) là sử dụng công thức: 1 n n UP o Chính xác hơn có thể sử dụng công thức: 4,0 3,0 n n UP o Hàm mật độ xác suất biểu diễn tốc độ thay đổi xác suất theo sự thay đổi giá trị điện áp dU UdP Uf Xác xuất để phóng điện xảy ra trong một thử nghiệm tại giá trị điện áp U + dU Để đặc trưng cho tập dữ liệu điện áp phóng điện theo phân phối chuẩn, giá trị điện áp phóng điện trung bình và độ lệch chuẩn được sử dụng n i iU n U 1 1 với Ui: điện áp phóng điện quan sát dUUfUdP 2 11 1 n i i UU n Độ lệch chuẩn thường được dùng để chỉ mức độ phân tán điện áp phóng điện xung quanh giá trị trung bình. Thông thường ký hiệu: %50UU Giá trị điện áp gây ra xác suất phóng điện bằng 0,5 Khi thiết kế thiết bị điện cao áp, yêu cầu cần phải biết giá trị điện áp tác dụng cao nhất mà không gây ra phóng điện thực tế, cần phải biết các giá trị điện áp gây ra xác suất phóng điện nhỏ (1-5% tùy thuộc vào người thiết kế và tiêu chuẩn thiết kế) Xác định điện áp có xác suất phóng điện nhỏ bằng phương pháp thí nghiệm có chi phí cao và tốn thời gian sử dụng mô hình toán học để biểu diễn hàm phân phối xác suất của các số liệu thí nghiệm ở giá trị xác suất phóng điện lớn kết hợp với phương pháp ngoại suy Theo kinh nghiệm, xung quanh giá trị xác suất phóng điện 50%, hàm phân phối chuẩn (Gauss) và phân phối Weibull khớp hoàn toàn số liệu thí nghiệm dU UU UP U 2 2 1 exp 2 1 )( b UU UU UP min63 minexp1)( Gauss Weibull 3 tham số Với: Umin: điện áp thấp nhất có thể gây phóng điện b: hệ số hình dạng U63: giá trị điện áp gây xác suất phóng điện là 63,2% Thực tế rất khó xác định Umin, nên có thể xem Umin = 0 phân phối Weibull 2 tham số b U U UP 63 exp1)( Nhược điểm của phân phối Weibull là tồn tại một vài cách kết hợp 3 tham số đều khớp với số liệu thí nghiệm Tại vùng xác suất cực nhỏ và cực lớn, phân phối chuẩn không khớp dữ liệu, phân phối Weibull khớp hoàn toàn dữ liệu thí nghiệm sử dụng phân phối Weibull Phân phối chuẩn Phân phối Weibull 3. Ảnh hưởng của diện tích bề mặt điện cực và thể tích khối cách điện 1 2 100 Hệ thống cách điện bao gồm 100 phần tử cách điện nối song song Mỗi phần tử có xác suất phóng điện là P1(U) (xác định từ thí nghiệm) Xác suất phóng điện của hệ thống 100 phần tử là PN(U) UPUPN 1?)( Ví dụ: cần xác định xác suất phóng điện của 100 m cáp trong khi chỉ có thể thí nghiệm với 1 m cáp Xác suất để không bị phóng điện NN UPUPUPUPUP 1111 11...1.1)(1 b U U UP 63 exp1)(Mà: b N b b b b b N b N U U UN U U U N U U N U U UP 63 63 /1 63 /1 6363 exp1 exp1.exp1 exp1exp1)( 6363 UU N Đồ thị dịch về phía trái Xác suất bị phóng điện Ảnh hưởng của thể tích b bN UN U UP 63 /1 exp1)( Với: N = V/Vo V: tổng thể tích khối cách điện; Vo: thể tích đơn vị để xác định xác suất phóng điện từ thí nghiệm Ảnh hưởng của diện tích bề mặt điện cực b bN UN U UP 63 /1 exp1)( Với: N = A/Ao A: tổng diện tích bề mặt điện cực; Ao: diện tích đơn vị để xác định xác suất phóng điện từ thí nghiệm 4. Cách sử dụng giấy Weibull yUbUbUP U U UP U U UP b b 63 63 63 lnln1lnln 1ln exp1)( Hàm phân phối xác suất 2 tham số ax c y = ax+c Đồ thị Weibull có dạng đường thẳng Đồ thị Weibull Độ dốc của đồ thị Weibull chính là hệ số hình dạng b. Hệ số b càng lớn độ phân tán dữ liệu càng nhỏ 12 12 xx yy b Với: Ux UbUby ln lnln 63 Giấy Weibull - Trục y: tỉ lệ log kép - Trục x: tỉ lệ log đơn - Đường chỉ thị hệ số hình dạng - Đường ngang chỉ thị xác suất có giá trị 63,2% b = 1, 10, 20, 30, .100, 200.1000, 2000 Kẻ đường song song xác định được hệ số b Hệ số b có thể xác định bằng công thức
File đính kèm:
 bai_giang_ky_thuat_cao_ap_chuong_8_xu_ly_du_lieu_dien_ap_dan.pdf
bai_giang_ky_thuat_cao_ap_chuong_8_xu_ly_du_lieu_dien_ap_dan.pdf

