Bài giảng Dụng cụ bán dẫn - Chương 3: Các hiện tượng vận chuyển hạt dẫn - Hồ Trung Mỹ
Độ linh động
Ta xét một mẫu bán dẫn loại N với nồng độ donor đều trong
điều kiện cân bằng nhiệt.
Dưới trạng thái cân bằng nhiệt, nhiệt năng trung bình của một
điện tử ở dãi dẫn có thể được lấy từ các định lý cân bằng
vùng năng lượng, 1/2 kT năng lượng cho mỗi bậc tự do, với k
là hằng số Boltzmann's và T là nhiệt độ tuyệt đối. Điện tử
trong bán dẫn có 3 bậc tự do (trong không gian). Do đó động
năng của điện tử được cho bởi
với m
n là khối lượng hiệu dụng của điện tử và vth là vận tốc
nhiệt trung bình. Ở nhiệt độ phòng (300oK), vth ~ 107cm/s với
Si và GaAs.6
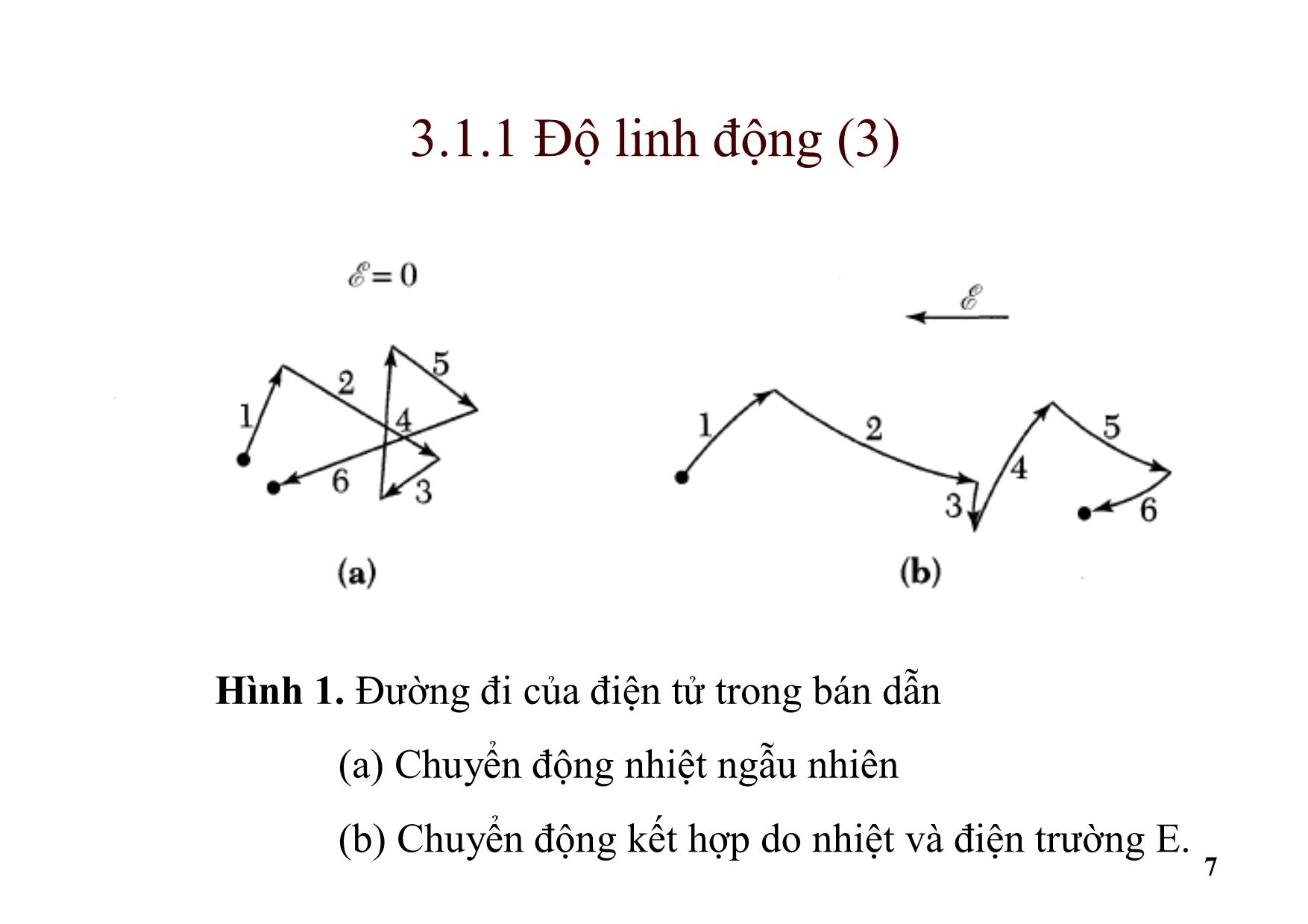
Do nhiệt, điện tử chuyển động nhanh theo mọi hướng.
Chuyển động nhiệt của mỗi điện tử có thể được xem như sự nối
tiếp của tán xạ ngẫu nhiên từ các va chạm với các nguyên tử trong
mạng, các nguyên tử tạp chất, và các trung tâm tán xạ khác (xem
minh họa ở hình 1a). Chuyển động ngẫu nhiên của các điện tử dẫn
đến sự dịch chuyển của điện tử là zero trong 1 khoảng thời gian đủ
dài.
Khoảng cách trung bình giữa các va chạm đgl đường đi tự do
trung bình (mean free path), và thời gian trung bình giữa các va
chạm đgl thời gian tự do trung bình (average free time) C.
Giá trị tiêu biểu cho đường đi tự do trung bình là 10-5cm và
C ~ 1ps=10-12s.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Dụng cụ bán dẫn - Chương 3: Các hiện tượng vận chuyển hạt dẫn - Hồ Trung Mỹ

46 3.2.2 Quan hệ Einstein (2) Thí dụ 5: Các hạt dẫn thiểu số (lỗ) được bơm vào 1 điểm của mẫu bán dẫn N. Áp đặt 1 điện trường 50V/cm vào mẫu bán dẫn, và điện trường này làm các hạt dẫn thiểu số này đi được 1 đoạn đường 1cm trong 100 ps. Hãy tìm vận tốc trôi và độ khuếch tán của các hạt dẫn thiểu số này. Bài giải. 47 48 Khi có thêm điện trường trong bán dẫn có gradient nồng độ, sẽ có cả hai dòng trôi và dòng khuếch tán. Mật độ dòng điện tổng cộng ở bất cứ điểm nào là tổng của các thành phần trôi và khuếch tán: với E là điện trường theo hướng x. Ta cũng có biểu thức tương tự cho dòng lỗ: Ta sử dụng dấu âm trong phương trình (32) vì với gradient lỗ dương, các lỗ sẽ khuếch tán theo hướng x âm. Ta có mật độ dòng điên tổng cộng: Ba biểu thức (31 33) tao thành các phương trình mật độ dòng điện. Các phương trình này quan trọng cho biệc phân tích các hoạt động của dụng cụ dưới điện trường thấp. Tuy nhiên với điện trường đủ cao, các số hạng đại điện cho vận chuyển trôi sẽ được thay thế bằng vận tốc bão hoà vs. 3.2.3 Các phương trình mật độ dòng điện 49 3.3 Các quá trình sinh và tái hợp 50 Các quá trình sinh và tái hợp Ở điều kiện cân bằng nhiệt, quan hệ pn=ni2 thoả. Nếu có thêm hạt dẫn dôi ra trong bán dẫn để pn>ni2, ta có trạng thái không cân bằng.Quá trình tạo thêm các hạt dẫn thừa được gọi là bơm hạt dẫn (carrier injection). Phần lớn các dụng cụ bán dẫn hoạt động bằng cách tạo ra các hạt dẫn thêm vào các giá trị ở cân bằng nhiệt. Ta có thể thêm hạt dẫn thừa bằng kích thích quang hoặc phân cực thuận chuyển tiếp p-n. Bất cứ khi nào điều cân bằng nhiệt bị ảnh hưởng (nghĩa là pn khác ni2), sẽ tồn tại các quá trình hồi phục về trạng thái cân bằng nhiệt (nghĩa là pn = ni2). Trong trường hợp bơm các hạt dẫn thừa, cơ chế hồi phục về cân bằng nhiệt là tái hợp các hạt dẫn thiểu số được bơm vào với các hạt dẫn đa số. Tùy theo bản chất của quá trình tái hợp, năng lượng giải phóng từ quá trình tái hợp có thể bức xạ ra photon hoặc tiêu tán nhiệt trong mạng tinh thể. Khi có phát xạ photon, người ta gọi đó là tái hợp có bức xạ (radiative recombination), ngược lại thì gọi là tái hợp không có bức xạ (nonradiative recombination) Các hiện tượng tái hợp có thể chia ra làm các quá trình trực tiếp và gián tiếp. Tái hợp trực tiếp cũng còn được gọi là tái hợp từ dải đến dải (band- to-band recombination), thông thường tái hợp này có nhiều trong các bán dẫn khe năng lượng trực tiếp như GaAs, trái lại tái hợp gián tiếp qua các trung tâm tái hợp khe năng lượng trong các bán dẫn khe năng lượng gián tiếp như Si. 51 © E. F. Schubert 51 Radiative and Nonradiative Recombination • Recombination rate is proportional to the product of the concentrations of electrons and holes, i.e. R = B n p, where B = bimolecular recombination coefficient, n = electron concentration, p = hole concentration • Non-radiative recombination creates heat instead of light R = B n p 52 Xét bán dẫn khe năng lượng trực tiếp ở điều kiện cân bằng nhiệt. Sự dao động nhiệt liên tục của các nguyên tử trong mạng tinh thể làm cho 1 số liên kết giữa các nguyên tử sẽ bị phá vở. Khi 1 liên kết bị phá vở thì sẽ sinh ra một cặp điện tử-lỗ. Theo giản đồ năng lượng, nhiệt năng làm cho một điện tử hóa trị chuyển lên dải dẫn, để lại lỗ [trống] ở dải hóa trị. Quá trình này được gọi là sinh hạt dẫn và được biểu diễn bằng tốc độ sinh Gth (số cặp điện tử-lỗ được sinh ra trong 1 giây trên 1 cm3) trong hình 10a. Khi điện tử chuyển từ dải dẫn về dải hóa trị thì sẽ mất đi 1 cặp điện tử-lỗ. Quá trình này được gọi là tái hợp; nó được biểu diễn bằng tốc độ tái hợp Rth trong hình 10a. Dưới các điều kiện cân bằng nhiệt, tốc độ sinh Gth phải bằng tốc độ tái hợp Rth để các nồng độ hạt dẫn giữ không đổi và vẫn duy trì điều kiện pn=ni2. 3.3.1 Sự tái hợp trực tiếp 53 Hình 10. Sự sinh và tái hợp trực tiếp của các cặp điện tử-lỗ: a) ở điều kiện cân bằng nhiệt b) dưới điều kiện được chiếu sáng 3.3.1 Sự tái hợp trực tiếp (2) 54 Khi có các hạt dẫn thừa được thêm vào bán dẫn khe năng lượng trực tiếp, xác suất để các điện tử và lỗ tái hợp trực tiếp sẽ cao, bởi vì đáy của dải dẫn và đỉnh dải hóa trị thẳng hàng và không cần thêm momentum để chuyển tiếp qua khe năng lượng. Tốc độ tái hợp trực tiếp R sẽ tỉ lệ với số điện tử khả dụng trong dải dẫn và số lỗ khả dụng trong dải hóa trị; nghĩa là, với là hằng số tỉ lệ. Như đã bàn trước đây, ở điều kiện cân bằng nhiệt, tốc độ tái hợp phải được cân bằng bởi tốc độ sinh. Do đó, với bán dẫn loại N, ta có Trong ký hiệu này, đối với nồng độ hạt dẫn: chỉ số thứ nhât chỉ loại bán dẫn và chỉ số thứ hai "o" chỉ đại lượng khi ở điều kiện cân bằng nhiệt. (TD: nno chỉ nồng độ điện tử ở bán dẫn loại N ở điều kiện cân bằng nhiệt). Khi ta chiếu sáng vào bán dẫn để tạo ra các cặp điện tử-lỗ với tốc độ GL (hình 10b), các nồng độ hạt dẫn ở trên các giá trị cân bằng của chúng. Tốc độ tái hợp và sinh lúc này là với n và p là những nồng độ hạt dẫn thừa, được cho bởi và n = p giữ cho trung hòa điện tích trên bán dẫn. 3.3.1 Sự tái hợp trực tiếp (3) 55 Tốc độ thay đổi nồng độ lỗ được cho bởi Ở trạng thái xác lập, dpn/dt =0. Từ phương trình (39), ta có với U là tốc độ tái hợp. Thay các phương trình (35) và (36) vào phương trình (40) cho Đối với bơm mức thấp p, pno << nno, phương trình (41) được đơn giản thành Do đó, tốc độ tái hợp tỉ lệ với nồng độ hạt dẫn thiểu số thừa. Hiển nhiên, U=0 ở điều kiện cân bằng nhiệt. Hằng số tỉ lệ 1/nno được gọi là thời gian sống t của các hạt dẫn thiểu số thừa, hoặc với 3.3.1 Sự tái hợp trực tiếp (4) 56 Ý nghĩa vật lý của thời gian sống có thể được minh họa tốt nhất bằng đáp ứng quá độ của dụng cụ sau khi lấy nguồn sáng đi một cách đột ngột. Xét mẫu bán dẫn loại N như trong hình 11a, nó được chiếu ánh sáng vào và có các cặp điện tử-lỗ được sinh ra trong suốt mẫu bán dẫn với tốc độ sinh GL. Biểu thức phụ thuộc thời gian được cho bởi phương trình (39). Ở trạng thái xác lập, từ các phương trình 40 và 43: hoặc Nếu ở thời điểm bất kỳ, thí dụ t=0, ánh sáng đột ngột bị tắt, các điều kiện biên là pn(t = 0) = pno + pGL, được cho bời phương trình (45a) và pn(t c) = pno. Biểu thức phụ thuộc thời gian của phương trình (39) trở thành và nghiệm của nó là 3.3.1 Sự tái hợp trực tiếp (5) Thời gian sống 57 3.3.1 Sự tái hợp trực tiếp (6) – Thời gian sống Hình 11. Sự suy giảm của các hạt dẫn bị kích thích bằng ánh sáng. (a) Mẫu bán dẫn loại N dưới chiếu ánh sáng không đổi. (b) Sự suy giảm của các hạt dẫn thiểu số (lỗ) theo thời gian. (c) Sơ đồ đo thời gian sống của hạt dẫn thiểu số. 58 Hình 11b cho thấy sự thay đổi của pn theo thời gian. Các hạt dẫn thiểu số tái hợp với các hạt dẫn đa số và suy giảm theo hàm mũ với thời hằng p, mà tương ứng với thời gian sống được định nghĩa trong phương trình (44). Trường hợp này minh họa ý tưởng chính của việc đo thời gian sống hạt dẫn bằng cách dùng phương pháp quang dẫn. Hình 11c minh họa cách thiết lập sơ đồ đo. Những hạt dẫn thừa (được sinh ra đều khắp trong mẫu bán dẫn bởi xung ánh sáng) làm gia tăng tức thời độ dẫn điện. Sự gia tăng độ dẫn điện làm cho sụt áp trên mẫu giảm xuống khi có dòng điện không đổi chạy qua. Sự suy giảm độ dẫn điện có thể được quan sát trên dao động ký và ta đo được thời gian sống của các hạt dẫn thiểu số thừa. 3.3.1 Sự tái hợp trực tiếp (7) – Thời gian sống 59 Với các bán dẫn khe năng lượng gián tiếp như Si, quá trình tái hợp trực tiếp thì không thể xảy ra, bởi vì các điện tử ở đáy dải dẫn có momentum khác không so với các lỗ ở đỉnh dải hóa trị. Sự chuyển tiếp trực tiếp mà bảo tồn cả năng lượng và momentum thì không thể không có tương tác đồng thời với mạng tinh thể. Do đó quá trình tái hợp chính trong những bán dẫn như vậy là chuyển tiếp gián tiếp qua các trạng thái năng lượng được cục bộ hóa trong khe năng lượng dải cấm. Những trạng thái hoạt động như những cục đá tạm dừng giữa dải dẫn và dải hóa trị. Hình 12 cho thấy nhiều chuyển tiếp khác nhau xảy ra trong các quá trình tái hợp qua các trạng thái mức trung gian (cũng được gọi là các trung tâm tái hợp). Ta minh họa trạng thái thay đổi của trung tâm trước khi và sau khi mỗi một trong bốn chuyển tiếp xảy ra. Các mũi tên trong hình vẽ chỉ chuyển tiếp của điện tử trong 1 quá trình cụ thể. Minh họa này cũng dùng cho trường hợp của 1 trung tâm tái hợp với mức năng lượng trung hòa khi không bị chiếm bởi điện tử và âm khi bị chiếm bởi điện tử. 3.3.2 Sự tái hợp gián tiếp 60 3.3.2 Sự tái hợp gián tiếp (2) Hình 12. Các quá trình sinh-tái hợp gián tiếp ở điều kiện cân bằng nhiệt. 61 Trong tái hợp gián tiếp, suy ra tốc độ tái hợp thì phức tạp hơn (xem phụ lục I), tốc độ tái hợp được tính theo với vth là vận tốc nhiệt của các hạt dẫn (phương trình 1), và n là phần ngang bắt được của các điện tử. Đại lượng n mô tả sự công hiệu của trung tâm bắt điện tử là số đo cho biết điện tử tới gần trung tâm bao nhiêu sẽ bị bắt. p là phần ngang bắt được của các lỗ. Ta có thể đơn giản hóa biểu thức của U theo Et bằng cách giả thiết n=p =0 . Khi đó phương trình 48 trở thành Dưới điều kiện bơm thấp trong bán dẫn loại N để nn >> pn, tốc độ tái hợp có thể được viết lại như sau Tốc độ tái hợp với tái hợp gián tiếp được cho bởi cùng biểu thức trong phương trình 43; tuy nhiên. p phụ thuộc vào những vị trí của các trung tâm tái hợp. 3.3.2 Sự tái hợp gián tiếp (3) 62 Hình 13 cho thấy các liên kết ở bề mặt bán dẫn. Do sự bất liên tục đột ngột của cấu trúc mạng tinh thể ở bề mặt, một số lớn các trạng thái năng lượng bị cục bố hóa hoặc có thể có các trung tâm sinh-tái hợp ở miền bề mặt. Những trạng thái năng lượng này, được gọi là những trạng thái bề mặt (surface states), có thể làm tăng nhiều tốc độ tái hợp ở bề mặt. Sự tái hợp bề mặt tương tự với những gì đã xét ở những trung tâm bên trong. Tổng số các hạt dẫn tái hợp ở bề mặt trên 1 đơn vị diện tích trong 1 giây có thể được biểu diễn với dạng tương tự phương trình 48. Với điều kiện bơm thấp, và với trường hợp giới hạn ở đó nồng độ điện tử ở bề mặt chủ yếu bằng nồng độ hạt dẫn đa số ở phần khối, tổng số hạt dẫn tái hợp ở bề mặt trên 1 đơn vị diện tích trong 1 giây có thể được đơn giản hóa thành với ps chỉ nồng độ lỗ ở bề mặt, và Nst là mật độ trung tâm tái hợp trên 1 đơn vị diện tích trong miền bề mặt. Vì tích số vthpNst có thứ nguyên là cm3/giây, nó được gọi là vận tốc tái hợp bề mặt bơm thấp Slr: 3.3.3 Sự tái hợp bề mặt 63 3.3.3 Sự tái hợp bề mặt (2) Hình 13. Sơ đồ các liên kết ỏ bề mặt bán dẫn sạch. Những liên kết này đẳng hướng (anisotropic) và khác với các liên kết trong miền khối. 64 Surface Recombination 65 Sự tái hợp cặp điện tử-lỗ Truyền năng lượng hoặc momentum đến hạt thứ ba (điện tử hay lỗ) Thí dụ Tái hợp trực tiếp giải phóng năng lượng Điện tử thứ hai trong dải dẫn hấp thu năng lượng và trở thành điện tử có năng lượng Điện tử này mất năng lượng vào mạng tinh thể bởi các sự kiện tán xạ Quan trọng khi pha tạp chất nhiều hoặc ở mức bơm cao (high injection level) RAug=Bn2p hoặc Bnp2 với hằng số B phụ thuộc nhiều vào nhiệt độ Quá trình Auger liên quan với 3 hạt. 3.3.4 Sự tái hợp Auger 66 3.4 Phương trình liên tục 67 Trong những phần trước ta đã xét các hiệu ứng riêng biệt như trôi do điện trường, khuếch tán do gradient nồng độ, và tái hợp các hạt dẫn qua các trung tâm tái hợp ở các mức trung gian. Bây giờ ta xét toàn bộ hiệu ứng khi trôi, khuếch tán, và tái hợp xảy ra đồng thời trong vật liệu bán dẫn. Phương trình cho thấy tất cả các hiệu ứng này được gọi là phương trình liên tục (continuity equation). Để suy ra phương trình liên tục 1 chiều cho điện tử, ta xét một miếng mỏng rất nhỏ với độ dày dx tại x (Hình 15). Số điện tử trong miếng mỏng có thể tăng do dòng điện chạy vào miếng mỏng và sinh hạt dẫn trong miếng mỏng. Tốc độ tăng toàn bộ của điện tử là tổng đại số của 4 thành phần: số điện tử đi vào miếng mỏng tại x, trừ với số điện tử đi ra tại x + dx, cộng với tốc độ điện tử được sinh ra, trừ với tốc độ điện tử bị tái hợp trong miếng mỏng. Hai thành phần đầu được tìm ra bằng cách chia các dòng điện tại mỗi bên của miếng mỏng bởi điện tích của điện tử. Tốc độ sinh và tái hợp được ký hiệu bằng Gn và Rn. Phương trình liên tục (2) 68 Phương trình liên tục (3) Hình 15. Luồng dòng điện và các quá trình sinh-tái hợp trong một miếng rất mỏng có độ dày dx 69 Tốc độ tổng cộng của sự thay đổi số điện tử trong miếng mỏng là với A là tiết diện ngang và Adx là thể tích của miếng mỏng. Khai triển Taylor cho dòng điện ở x + dx cho Như vậy ta có được phương trình liên tục cho điện tử: Tương tự, ta có thể suy ra phương trình liên tục cho lỗ, ngoại trừ dấu của số hạng thứ nhất ở vế phải phương trình 56 bị đổi dấu do điện tích dương với lỗ: Phương trình liên tục (4) 70 Ta có thể thay thế các biểu thức dòng điện từ các phương trình 31 và 32 và các biểu thức tái hợp từ phương trình 43 vào các phương trình 56 và 57. Trong trường hợp 1 chiều dưới điều kiện mức bơm thấp, phương trình liên tục cho các hạt dẫn thiểu số là Ngoài các phương trình liên tục, phương trình Poisson phải được thỏa, với s là hằng số điện môi bán dẫn và s là mật độ điện tích không gian là tổng đại số của mật hạt dẫn và các nồng độ tạp chất bị ion hóa, q(p - n + ND+- NA-) . Về nguyên tắc, các phương trình từ 58 đến 60 cùng với những điều kiện biên thích hợp cho nghiệm duy nhất. Bởi vì độ phức tạp về đại số của bộ phương trình này, trong phần lớn các trường hợp các phương trình được đơn giản hóa bằng các xấp xỉ vật lý để đạt được nghiệm dễ hơn. Phương trình liên tục (4) 71 2 n n n 2 2 P p P p p p x D L P P pL D 2 n n P 2 p 0 p p D x n n0 (0)p p N N nL D Tương tự, Chiều dài khuếch tán hạt dẫn thiểu số (1/4) Chapter 3 Carrier Action Xét trường hợp đặc biệt (xem hình 16): Bơm vào hạt dẫn thiểu số (lỗ) không đổi ở x = 0 Ở xác lập, không có hấp thu ánh sáng với x > 0 L 0 for 0G x Chiều dài khuếch tán lỗ LP được định nghĩa: 72 Chiều dài khuếch tán hạt dẫn thiểu số (2/4) Bán dẫn Si loại N 73 2 n n 2 2 P p p x L P P n ( ) x L x Lp x Ae Be n ( ) 0p n n0(0)p p P n n0( ) x Lp x p e Chapter 3 Carrier Action Lời giải tổng quát của phương trình là: A và B là những hằng số được xác định bởi các điều kiện biên: Do đó, ta có nghiệm là: 0B n0 A p • Về mặt vật lý, LP và LN biêu diễn khoảng cách trung bình mà hạt dẫn thiểu số có thể khuếch tán trước khi nó tái hợp với hạt dẫn đa số. Chiều dài khuếch tán hạt dẫn thiểu số (3/4) 74 2 p 437 cm V s P p kT D q P P pL D Chapter 3 Carrier Action Cho trước ND=1016 cm–3, τp = 10–6 s. Tính LP. 225.86 mV 437 cm V s 211.3cm s 2 611.3cm s 10 s 33.361 10 cm = 33.61 m Từ đồ thị, Chiều dài khuếch tán hạt dẫn thiểu số (4/4) 75 Tóm tắt các phương trình bán dẫn
File đính kèm:
 bai_giang_dung_cu_ban_dan_chuong_3_cac_hien_tuong_van_chuyen.pdf
bai_giang_dung_cu_ban_dan_chuong_3_cac_hien_tuong_van_chuyen.pdf

