Bài giảng Dụng cụ bán dẫn - Chương 2: Dải năng lượng và nồng độ hạt dẫn ở cân bằng nhiệt - Hồ Trung Mỹ
Control of Conductivity is the Key to
Modern Electronic Devices
Conductivity, σ, is the ease with which a given
material conducts electricity.
Ohms Law: V=IR or J=σE where J is current density
and E is electric field.
Metals: High conductivity
Insulators: Low Conductivity
Semiconductors: Conductivity can be varied by several
orders of magnitude.
It is the ability to control conductivity that make
semiconductors useful as “current/voltage control
elements”. “Current/Voltage control” is the key to
switches (digital logic including microprocessors
etc ), amplifiers, LEDs, LASERs, photodetectors,
etc.5
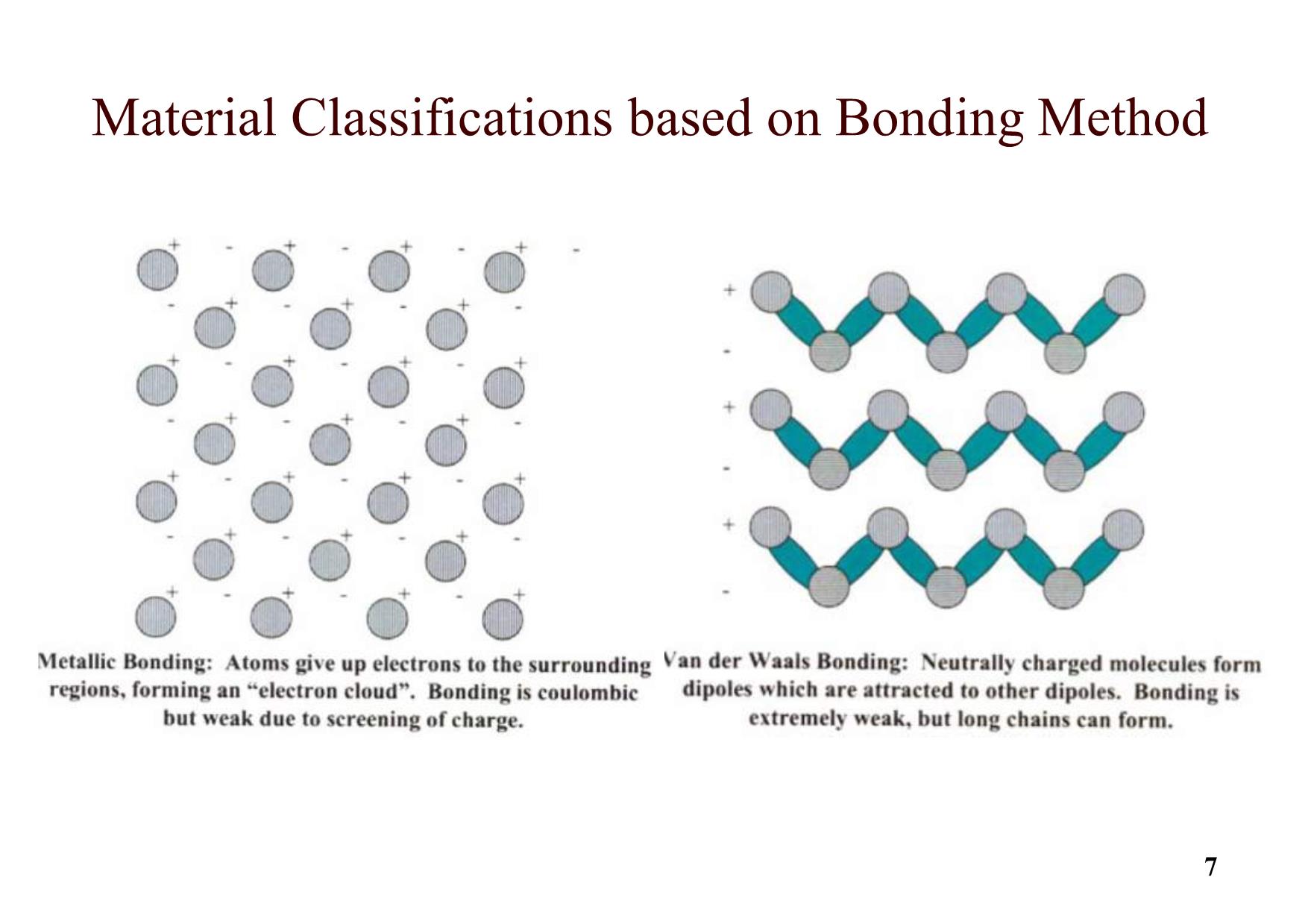
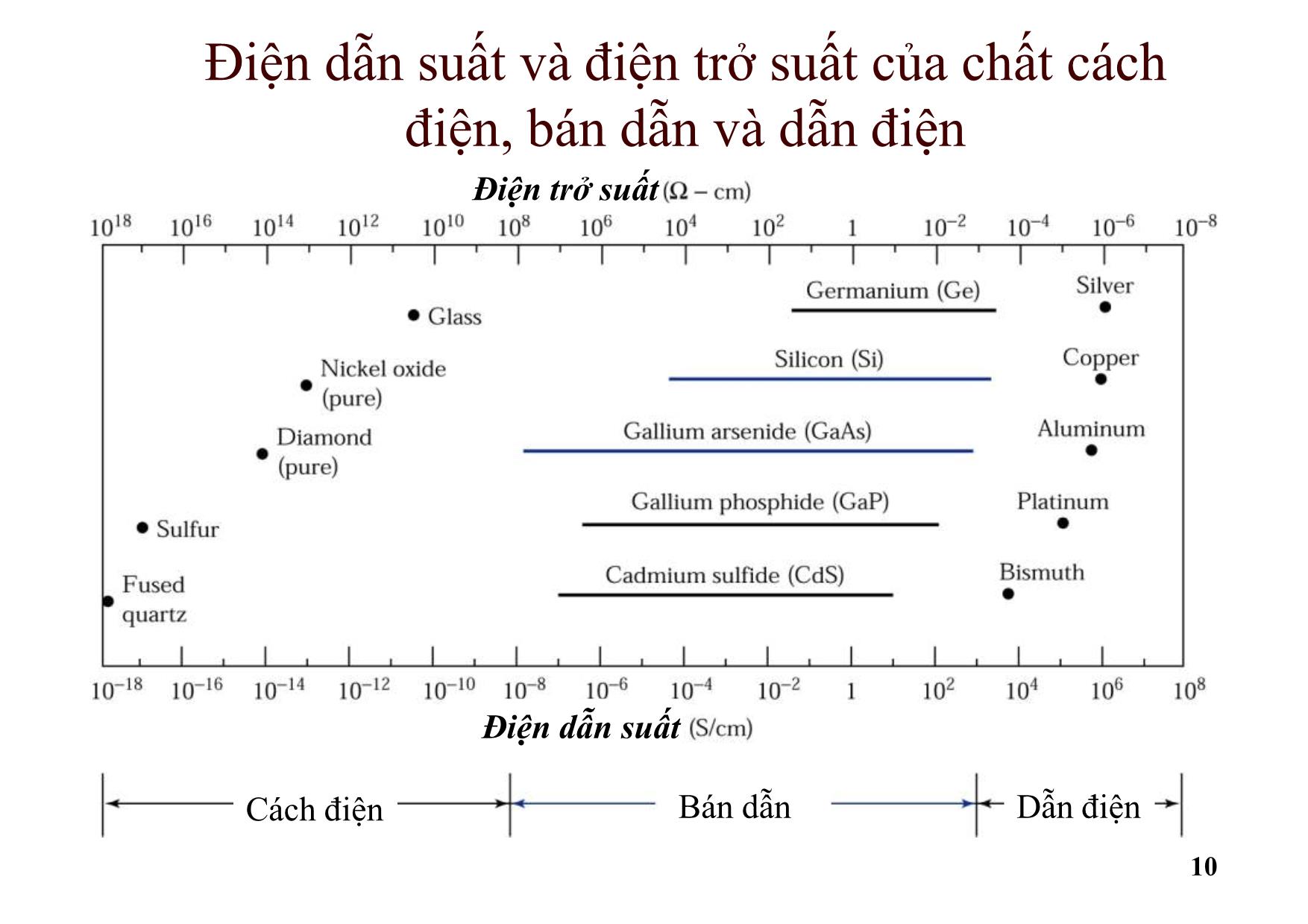
Classifications of Electronic Materials
Electrical/Computer engineers like to classify materials based
on electrical behavior (insulating, semi-insulating, and
metals).
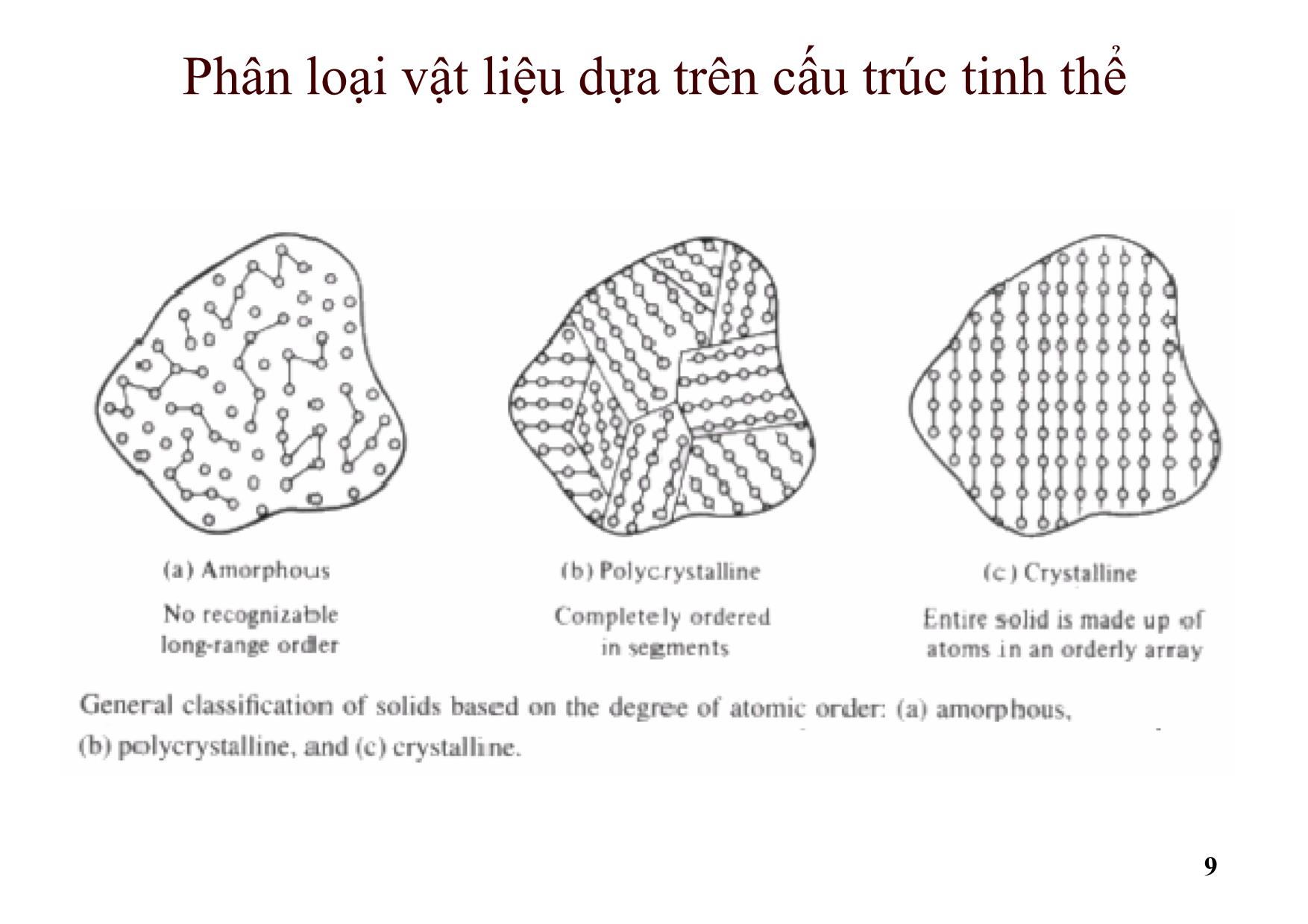
Materials Engineers/Scientists classify materials based on
bond type (covalent, ionic, metallic, or van der Waals), or
structure (crystalline, polycrystalline, amorphous, etc.).
In 20-50 years, EE’s may not be using semiconductors at all!!
Polymers or bio-electronics may replace them! However the
materials science will be the same!

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Dụng cụ bán dẫn - Chương 2: Dải năng lượng và nồng độ hạt dẫn ở cân bằng nhiệt - Hồ Trung Mỹ

uang tử (photon) của Einstein. Hiệu số năng lượng giữa 2 mức năng lượng n và m (năng lượng photon) được cho bởi: En ứng với mức năng lượng cao hơn. Chuyễn tiếp từ mức năng lượng cao hơn xuống thấp hơn dẫn đến mất năng lượng. Năng lượng được giải phóng dưới dạng photon, với f là tần số của ánh sáng được phát xạ. Tần số f và bước sóng tương ứng của ánh sáng được cho bởi: Nguyên tử Hydrogen (tt) 42 Những dải năng lượng Ta chuyển việc khảo sát từ nguyên tử đơn sang khảo sát chất rắn. Với một nguyên tử cách ly, các điện tử có các mức năng lượng rời rạc. Khi số p các nguyên tử cách ly được gom lại với nhau để tạo thành chất rắn, quỹ đạo của các điện tử ngoài cùng phủ lấp nhau và tương tác với nhau. Sự tương tác này bao gồm những lực hút và đẩy giữa các nguyên tử. Những lực hút giữa các nguyên tử gây ra sự dịch các mức năng lượng. Thay vì tạo thành những mức đơn, như trong trường hợp đơn nguyên tử, p mức năng lượng được tạo thành. Những mức năng lượng ở gần nhau. Khi p lớn, những mức năng lượng khác nhau tạo thành một dải liên tục. Những mức và do đó những dải có thể mở rộng lên nhiều eV tùy theo khoảng cách giữa các nguyên tử và phân tử. 43 Cấu trúc dải năng lượng của bán dẫn Bây giờ chúng ta chuyển từ mô tả tổng quát cấu trúc dải năng lượng trong chất rắn sang trường hợp cụ thể hơn của silicon. Một nguyên tử silicon cách ly có 14 điện tử. Trong 14 điện tử, có 10 điện tử chiếm những mức năng lượng sâu hơn. Do đó, bán kính quỹ đạo nhỏ hơn lực tách giữa những phân tử trong tinh thể. 10 điện tử bị liên kết chặt với các nguyên tử. Bốn điện tử dải hóa trị còn lại có liên kết yếu với lõi và có thể tham gia vào các phản ứng hóa học. Do đó, chúng ta có thể tập trung vào lớp vỏ ngoài cùng (mức n=3). Mức n=3 gồm các lớp vỏ con 3s (n=3 và l=0) và 3p (n=3 và l=1). Lớp vỏ con 3s có 2 mức trạng thái cho phép trên 1 nguyên tử và cả hai trạng thái được lắp bởi 1 điện tử (ở 0oK). Lớp vỏ con 3p có 6 trạng thái cho phép và 2 trong các trạn thái này được lắp bởi những điện tử còn lại. 44 Biểu diễn sơ đồ của nguyên tử silicon cách ly 45 Sự tạo thành những dải năng lượng trong silicon theo hàm khoảng cách giữa các nguyên tử trong mạng tinh thể. 46 Khe năng lượng (bandgap) Đáy của dải dẫn được gọi là EC và đỉnh của dải hóa trị được gọi là EV. Hiệu số năng lượng giữa đáy dải dẫn và đỉnh dải hóa trị được gọi là khe năng lượng EG. Khe năng lượng EG = EC – EG ở giữa đáy dải dẫn và đỉnh dải hóa trị bằng bề rộng dải cấm. EG là năng lượng cần để phá vở liên kết trong bán dẫn để cho một điện tử trong dải dẫn và để một lỗ trống trong dải hóa trị. Sự thiếu hụt một điện tử trong dải hóa trị được coi là một lỗ [trống tự do]. Sự thiếu hụt trong dải hóa trị có thể được lấp bằng điện tử lân cận, mà dẫn đến sự dịch chuyển vị trí thiếu hụt, xem như lỗ di chuyển. Lỗ có điện tích dương. Cả hai điện tử và lỗ góp phần vào tạo nên dòng điện. 47 Nếu 1 điện tử được kích thích vào dải dẫn, nó có thể di chuyển tự do trong tinh thể, từ đó điện tử có thể được xem như một hạt trong không gian tự do. Sự truyền lan của điện tử tự do có thể được mô tả bằng hàm sóng, là lời giải của phương trình Schrödinger. Hàm sóng cho điện tử tự do được cho bởi với k là vector sóng có phương trình sau: p là momentum (mô-măn) của điện tử. Do biểu thức này, năng lượng điện tử có thể được cho trước theo hàm của vector sóng. Ta nói về biểu diễn không gian k. Các dải năng lượng lúc này có thể được xác định theo hàm của vector k. 2.5.2 Giản đồ năng lượng-momentum 48 Giản đồ năng lượng-momentum (tt) 49 Khối lượng hiệu dụng của điện tử mn phụ thuộc vào tính chất của bán dẫn. Nếu ta có quan hệ năng lượng-momentum như sau thì ta có thể tính được khối lượng hiệu dụng qua đạo hàm bậc 2 của E theo p: Do đó khi parabola càng hẹp, tương ứng với đạo hàm bậc 2 càng lớn, thì khối lượng hiệu dụng càng nhỏ. Ta có biểu thức tương tự với lỗ (có khối lượng hiệu dụng mp). Khái niệm khối lượng hiệu dụng rất hữu ích vì nó giúp xem điện tử và lỗ như các hạt tích điện cổ điển. 50 TD về giản đồ năng lượng - momentum m0 = khối lượng của điện tử tự do 51 Giản đồ năng lượng-momentum [cgl giản đồ dải năng lượng] của (a) bán dẫn gián tiếp (Td: Si ) và (b) bán dẫn trực tiếp (Td: GaAs) • GaAs được gọi là bán dẫn trực tiếp vì nó không cần sự thay đổi momentum để chuyển điện tử từ dải hóa trị sang dải dẫn. • Si được gọi là bán dẫn gián tiếp vì nó cần sự thay đổi momentum để chuyển điện tử từ dải hóa trị sang dải dẫn. 52 2.5.3 Sự dẫn điện trong kim loại, bán dẫn và chất cách điện Hình 19 cho thấy giản đồ dải năng lượng của 3 loại chất rắn: dẫn điện (kim loại), bán dẫn, và cách điện. Chất dẫn điện: có điện trở suất rất thấp và dải dẫn được đổ đầy 1 phần điện tử tự do (như đồng) hoặc phủ lấp dải hóa trị (như kẽm và chì) để không có khe năng lượng. Chất bán dẫn: có khe năng lượng < 4eV. Ở T=0K, tất cả điện tử ở dải hóa trị và không có điện tử ở dải dẫn cách điện. Ở nhiệt độ phòng, do nhiệt năng kích thích 1 số điện tử vào dải dẫn dẫn điện (kém) Chất cách điện: có khe năng lượng > 4eV (như SiO2). Các điện tử hóa trị tạo nên liên kết mạnh với các nguyên tử lân cận. Ở nhiệt độ phòng, nhiệt năng không đủ kích thích các điện tử vào dải dẫn không dẫn điện cách điện. 53 54 Phân loại vật liệu theo khe năng lượng 55 So sánh giữa mô hình liên kết hóa trị và mô hình dải năng lượng Eg = năng lượng cần làm gãy 1 liên kết đồng hóa trị Không có liên kết bị phá vở Không có điện tử trong dải dẫn và Không có trạng thái trống trong dải hóa trị Không có dòng điện Ở T = 0K Sinh cặp điện tử-lỗ Liên kết bị phá vở Điện tử (trong dải dẫn và) Lỗ (trạng thái trống trong dải hóa trị) Khi có kích thích là nhiệt năng hay quang năng - Những điện tử trong dải dẫn - Những lỗ (trạng thái trống) trong dải hóa trị Những hạt dẫn: 56 Một số thuật ngữ thường dùng trong lý thuyết dải năng lượng: Một số thuật ngữ thường dùng trong lý thuết dải năng lượng: NV: mật độ trạng thái hiệu dụng của dải hóa trị, đây là số lỗ tối đa trên 1 đơn vị thể tích mà ta có thể tìm thấy trong toàn bộ vùng hóa trị. NC: mật độ trạng thái hiệu dụng của dải dẫn, đây là số điện tử tối đa trên 1 đơn vị thể tích mà ta có thể tìm thấy trong toàn bộ dãi dẫn. n: nồng độ điện tử (electron concentration) là số điện tử trên 1 đơn vị thể tích trong dải dẫn. p: nồng độ lỗ (hole concentration) là số lỗ trống trên 1 đơn vị thể tích trong dải hóa trị. Chú ý: n và p còn được gọi là các nồng độ hạt dẫn (carrier concentration) vì chúng là những hạt mang điện tích tự do và chuyển động theo điện trường để tạo thành dòng điện. 57 2.6 Nồng độ hạt dẫn nội tại (Intrinsic concentrations) 58 Các tính chất vật liệu và hạt dẫn Bán dẫn thuần và bán dẫn có pha tạp chất (Intrinsic and extrinsic Semiconductors) Vật liệu được xem là bán dẫn thuần (còn gọi là bán dẫn nội tại hay tinh khiết) nếu vật liệu chứa một lượng tạp chất tương đối nhỏ. Vật liệu được xem là bán dẫn có pha tạp chất (còn gọi là bán dẫn ngoại lai) nếu vật liệu chứa một lượng tạp chất tương đối lớn. Bán dẫn ở cân bằng nhiệt Ta giả sử đang xét bán dẫn thuần và bỏ qua các ảnh hưởng của tạp chất với bán dẫn. Ngoài ra ta giả sử bán dẫn ở cân bằng nhiệt, nghĩa là bán dẫn không bị tác động bởi các kích thích bên ngoài như ánh sáng, áp suất hay điện trường. Bán dẫn được giữ ở nhiệt độ không đổi trên toàn bộ mẫu thử (nghĩa là không có gradient nhiệt độ trong chất bán dẫn). 59 Tính nồng độ điện tử Để có được nồng độ điện tử (số điện tử trên 1 đơn vị thể tích) trong bán dẫn nội tại, trước hết ta phải tìm mật độ điện tử trong 1 gia số năng lượng dE. Mật độ này n(E) được cho bởi tích của mật độ trạng thái N(E), nghĩa là mật độ của các trạng thái năng lượng được cho phép trên năng lượng E trên 1 đơn vị thể tích, với xác suất chiếm trạng thái năng lượng đó F(E). Như vậy nồng độ điện tử trong dải dẫn có được bằng cách lấy tích phân N(E) F(E) dE từ đáy của dải dẫn (E, để cho đơn giản ban đầu cho E=0) đến đỉnh của dải dẫn Etop: với n theo cm-3, N(E) theo (cm3eV)–1. 60 Hàm phân bố Fermi-Dirac Xác suất mà 1 điện tử chiếm 1 trạng thái điện tử với năng lượng E được cho bởi hàm phân bố Fermi-Dirac, còn được gọi là hàm phân bố Fermi. với k là hằng số Boltzmann, T là nhiệt độ tuyệt đối theo độ Kelvin, và EF là mức năng lượng Fermi. Năng lượng Fermi là năng lượng mà ở đó xác suất được chiếm bởi điện tử chính xác bằng 0.5. Phân bố Fermi được minh họa ở hình 20 với các nhiệt độ khác nhau. Chú ý là F(E) đối xứng quanh mức năng lượng Fermi. Với những năng lượng mà lớn hơn (hoặc nhỏ hơn) 3kT so với năng lượng Fermi, số hạng mũ > 20 (hoặc <0.05). Phân bố Fermi có thể được xấp xỉ bằng các biểu thức đơn giản hơn: Phương trình 11b có thể được xem như xác suất của lỗ chiếm mức năng lượng E. 61 Hình 20. Hàm phân bố Fermi F(E) theo E – EF với các nhiệt độ khác nhau 62 Bán dẫn thuần ở cân bằng nhiệt 63 Mật độ trạng thái Ta có thể tính các mật độ trạng thái bằng phương trình Schrödinger. Tuy nhiên ta sẽ không bàn về việc suy ra hàm mật độ trạng thái. SV có thể đọc thêm trong phụ lục H của sách “Semiconductor Devices”, tác giả M.S Sze. với NC là mật độ trạng thái điện tử và NV là Mật độ trạng thái lỗ Mật độ trạng thái được xác định bởi một tham số vật liệu, đó là khối lượng hiệu dụng của điện tử (me) hay lỗ (mh). Do đó, mật độ trạng thái của điện tử và lỗ thường khác nhau. 64 Mức (hay năng lượng) Fermi EF và nồng độ hạt dẫn cân bằng 65 Phân bố Fermi-Dirac của điện tử Fe(E) và lỗ Fh(E). Cân bằng nhiệt Chất bán dẫn ở cân bằng nhiệt, nếu nhiệt độ ở mỗi vị trí của tinh thể là như nhau, dòng điện tổng cộng qua vật liệu bằng 0, và chất rắn không bị chiếu sáng. Ngoài ra ta còn giả sử rằng không có phản ứng hóa học tham dự. Do đó năng lượng Fermi trên toàn vật liệu là như nhau: EF = EF(x, y, z) = const 66 Năng lượng Fermi trong chất rắn 67 Phân bố Boltzmann Chú ý: Các phương trình trên chỉ áp dụng cho bán dẫn ở điều kiện cân bằng (đkcb). 68 Nồng độ hạt dẫn nội tại 69 Nồng độ hạt dẫn nội tại ni 70 Biểu diễn n & p qua ni 71 TD các giá trị NC, NV và ni của 1 số bán dẫn thông dụng (ở 300oK) 72 2.6 Chất Donor và chất Acceptor Bán dẫn có pha tạp chất Bán dẫn loại P và bán dẫn loại N 73 Chất cho điện tử (donor) và chất nhận điện tử (acceptor) Khi bán dẫn bị pha tạp chất (với 1 lượng lớn tạp chất) thì người ta gọi nó là bán dẫn ngoại lai hay bán dẫn có pha tạp chất. Trong phần này ta sẽ xét ảnh hưởng của các acceptor và donor lên các tính chất của vật liệu. Ta sẽ tập trung xét pha tạp chất cho silicon. (a) Mạng tinh thể Si loại N với pha tạp chất bằng các nguyên tử donor As hay P (arsenic hay phosphorus). (b) Mạng tinh thể Si loại P với pha tạp chất bằng các nguyên tử acceptor B (boron). 74 Donors When a semiconductor is doped with impurities Extrinsic semiconductor The impurity energy level are introduced N-type Si with donor Arsenic atom with five valence electron Covalent bonds with its four neighboring Si atoms The fifth electron Relatively small bonding energy to its host arsenic atom Be “ionized” to become a conduction electron The arsenic atom is called a donor Silicon become n-type Because the addition of the negative charge carrier 75 Acceptors P-type Si with acceptor Boron atom with three valence electron An additional electron is “accepted” to form four covalent bonds around the boron A positive charged “hole” is created in the valence band Boron is an acceptor 76 Giản đồ dải năng lượng của bán dẫn loại N và bán dẫn loại P 77 Năng lượng ion hóa của các tạp chất trong Si và GaAs 78 2.7 Nồng độ hạt dẫn trong bán dẫn loại N và P 79 Bán dẫn loại N 80 Quan hệ giữa nồng độ điện tử n và nồng độ lỗ trong bán dẫn 81 Định luật tác động khối lượng (Mass action law) Còn được gọi là định luật tác dụng khối lượng: Trong điều kiện cân bằng nhiệt thì tích số của nồng độ hạt dẫn âm và dương tự do là hằng số, bất chấp lượng tạp chất donor và acceptor pha vào trong bán dẫn: np = ni2 Chú ý: Định luật này luôn luôn đúng với bán dẫn không suy biến! 82 Nồng độ hạt dẫn trong bán dẫn N Nếu cả hai tạp chất donor và acceptor đồng thời hiện diện thì tạp chất nào có nồng độ cao hơn sẽ quyết định loại dẫn điện nào trong bán dẫn. Mức Fermi phải tự điều chỉnh để duy trì sự trung hòa điện tích, nghĩa là tổng điện tích âm (các điện tử và các acceptor bị ion hóa) phải bằng tổng điện tích dương (các lỗ và các donor bị ion hóa). Dưới điều kiện ion hóa hoàn toàn, ta có Giải phương trình np=ni2 với (30) ta có Chỉ số n chỉ bán dẫn loại N 83 Trong bán dẫn N: hạt dẫn đa số là điện tử và hạt dẫn thiểu số là lỗ. Tương tự, ta có được nồng độ lỗ (hạt dẫn đa số) và điện tử (hạt dẫn thiểu số) trong bán dẫn P: Nồng độ hạt dẫn trong bán dẫn P (NA >ND) Chỉ số p chỉ bán dẫn loại P 84 Bán dẫn có bổ chính (Compensated Semiconductor) 85 Mức Fermi là hàm của nhiệt độ và nồng độ tạp chất Vị trí của mức Fermi trong giản đồ dải năng lượng EF = EC – kT ln (NC/ND) với bán dẫn N EF = EV + kT ln (NV/NA) với bán dẫn P Thế Fermi F = (Ei – EF)/q Dùng để xác định mức Fermi, Dùng để viết phương trình n và p gọn hơn Dấu của thế Fermi cho ta biết bán dẫn loại gì. Thế khối b = - F = (EF – Ei)/q - - 86 Hình 20 (a) Mức Fermi trong Si là hàm của nhiệt độ và nồng độ tạp chất T (K) 87 Ảnh hưởng của nhiệt độ đến nồng độ hạt dẫn (Td: Si loại N, xét nn) Ở nhiệt độ thấp Nhiệt năng không đủ ion hóa tất cả các tạp chất donor Một số điện tử bị “đóng băng” ở mức donor Nồng độ điện tử < nồng độ donor Khi tăng nhiệt độ Điều kiện để đạt được ion hóa hoàn toàn là nn=ND Khi tăng nhiệt độ thêm nữa Nồng độ điện tử không đổi trên 1 dải rộng nhiệt độ Miền ngoại lai Khi tăng nhiệt độ hơn nữa Nồng độ hạt dẫn nội tại trở nên có thể so sánh được với nồng độ donor Bán dẫn trở thành bán dẫn nội tại Nhiệt độ này phụ thuộc vào ND và Eg 88 Bán dẫn suy biến và không suy biến Phần lớn các dụng cụ điện tử, nồng độ điện tử và lỗ nhỏ hơn nhiều mật độ trạng thái hiệu dụng trong dải dẫn hay dải hóa trị. Mức Fermi tối thiểu cao hơn dải hóa trị 3kT hay thấp hơn dải dẫn 3kT. Trong trường hợp này ta gọi bán dẫn không suy biến (non- degenerated semiconductor). Khi pha rất nhiều tạp chất, các nồng độ tạp chất cao hơn các mật độ trạng thái hiệu dụng trong dải hóa trị và dải dẫn. Trong trường hợp như vậy ta có bán dẫn suy biến (degenerated semiconductor) và các mức Fermi dịch vào dải dẫn hay dải hóa trị. Dưới những điều kiện như vậy ta không thể áp dụng các phương trình đã được suy ở phần trước. Tuy nhiên, việc chế tạo bán dẫn suy biến cũng cần thiết. Thí dụ chế tạo các diode LASER cần đảo ngược mật độ, mà có thể chỉ đạt được việc này nếu bán dẫn là loại suy biến.
File đính kèm:
 bai_giang_dong_co_ban_dan_chuong_2_dai_nang_luong_va_nong_do.pdf
bai_giang_dong_co_ban_dan_chuong_2_dai_nang_luong_va_nong_do.pdf

