Bài giảng Điện tử số - Chương 2: Đại số Boole và các phương pháp biểu diễn hàm - Nguyễn Trung Hiếu
Phương pháp Bảng trạng thái
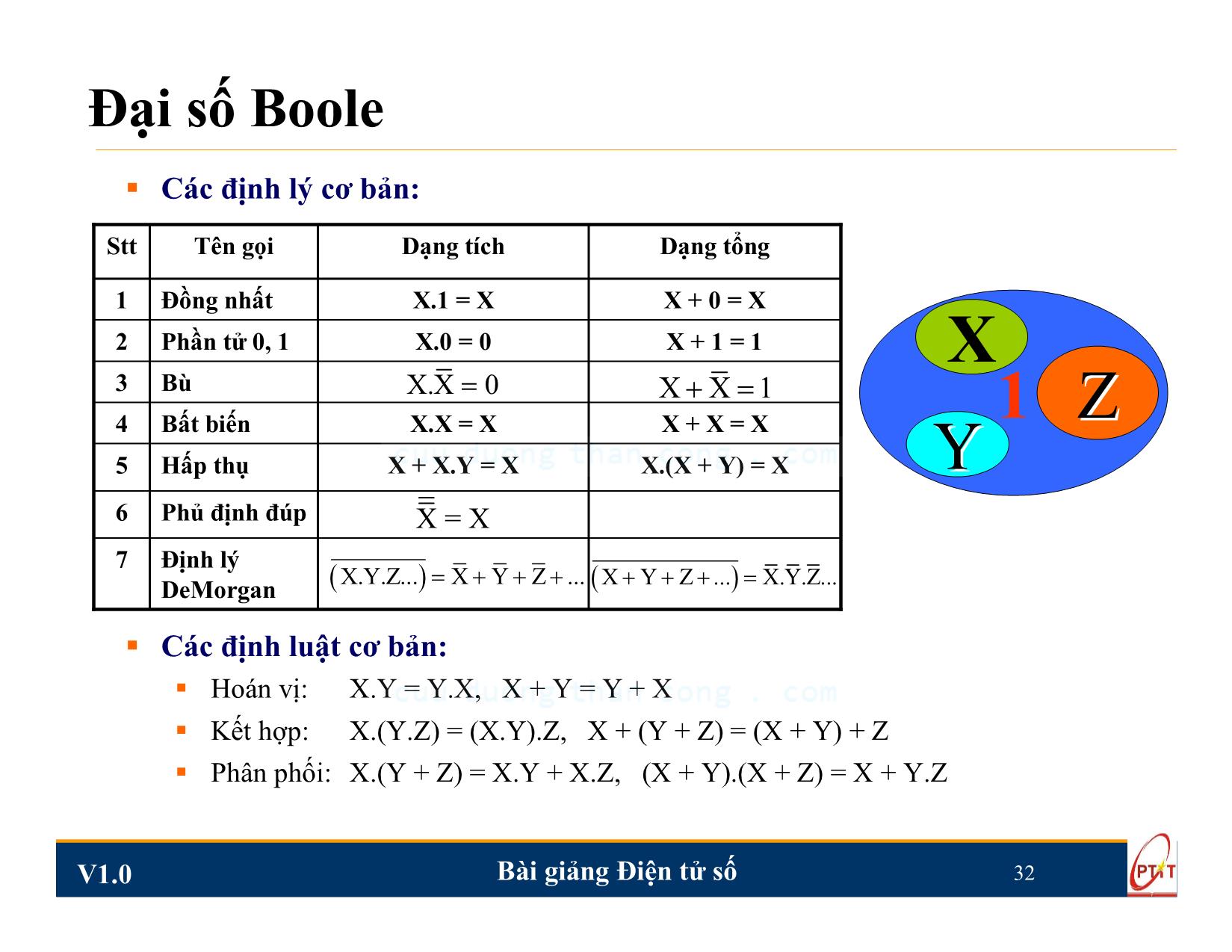
Liệt kê giá trị (trạng thái) mỗi biến
theo từng cột và giá trị hàm theo một
cột riêng (thường là bên phải bảng).
Bảng trạng thái còn được gọi là bảng
sự thật hay bảng chân lý.
Đối với hàm n biến sẽ có 2n tổ hợp
độc lập. Các tổ hợp này được kí hiệu
bằng chữ mi, với i = 0 ÷ 2n -1 và có
tên gọi là các hạng tích hay còn gọi
là mintex.
Vì mỗi hạng tích có thể lấy 2 giá trị
là 0 hoặc 1, nên nếu có n biến thì số
hàm mà bảng trạng thái có thể thiết
lập được sẽ là
Phương pháp Bảng Các nô (Karnaugh)
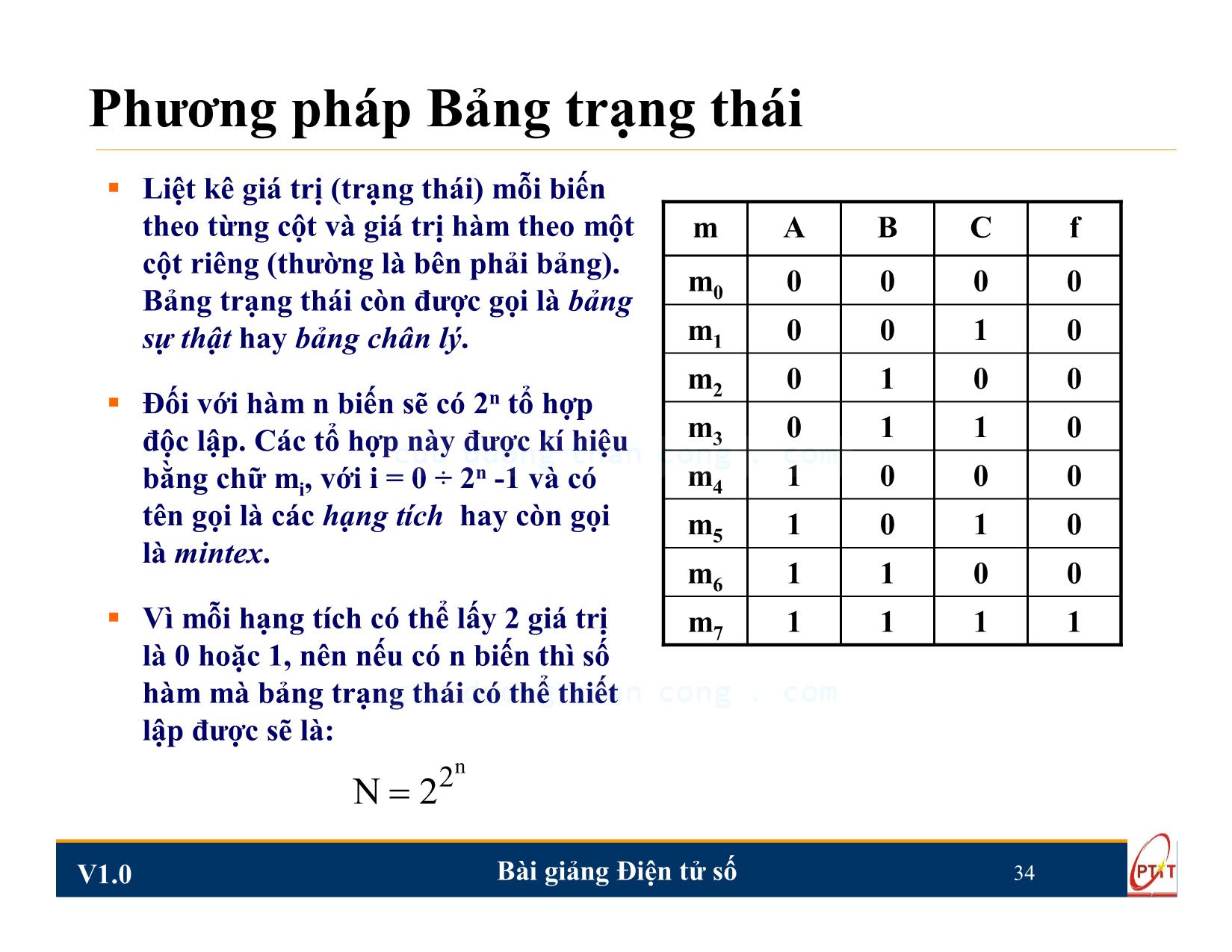
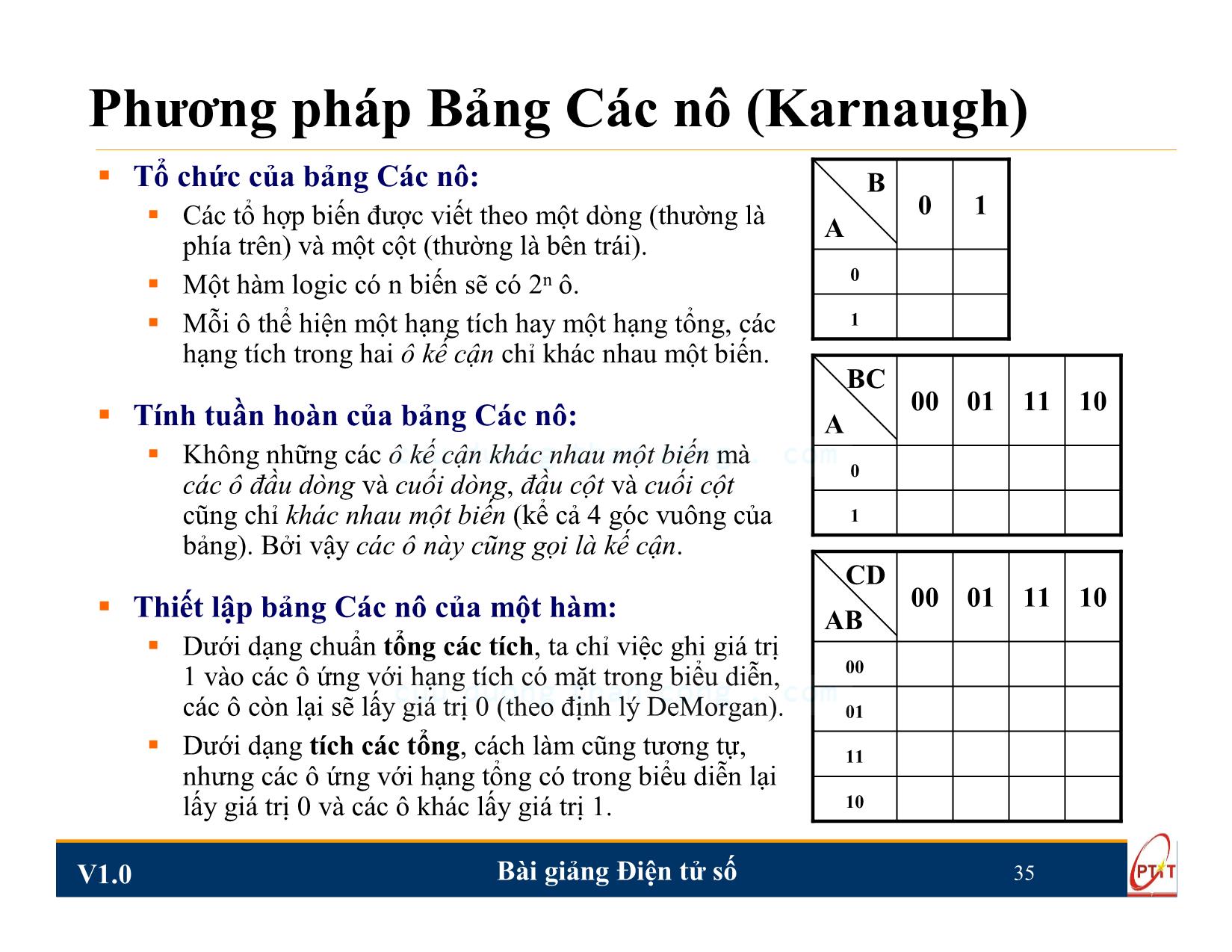
Tổ chức của bảng Các nô:
Các tổ hợp biến được viết theo một dòng (thường là
phía trên) và một cột (thường là bên trái).
Một hàm logic có n biến sẽ có 2n ô.
Mỗi ô thể hiện một hạng tích hay một hạng tổng, các
hạng tích trong hai ô kế cận chỉ khác nhau một biến.
Tính tuần hoàn của bảng Các nô:
Không những các ô kế cận khác nhau một biến mà
các ô đầu dòng và cuối dòng, đầu cột và cuối cột
cũng chỉ khác nhau một biến (kể cả 4 góc vuông của
bảng). Bởi vậy các ô này cũng gọi là kế cận.
Thiết lập bảng Các nô của một hàm:
Dưới dạng chuẩn tổng các tích, ta chỉ việc ghi giá trị
1 vào các ô ứng với hạng tích có mặt trong biểu diễn,
các ô còn lại sẽ lấy giá trị 0 (theo định lý DeMorgan).
Dưới dạng tích các tổng, cách làm cũng tương tự,
nhưng các ô ứng với hạng tổng có trong biểu diễn lại
lấy giá trị 0 và các ô khác lấy giá trị 1.

Trang 1

Trang 2
Trang 3

Trang 4
Trang 5
Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Điện tử số - Chương 2: Đại số Boole và các phương pháp biểu diễn hàm - Nguyễn Trung Hiếu

Bài giảng Điện tử sốV1.0 30 Nội dung Chương 1: Hệ đếm Chương 2: Đại số Boole và các phương pháp biểu diễn hàm Chương 3: Cổng logic TTL và CMOS Chương 4: Mạch logic tổ hợp Chương 5: Mạch logic tuần tự Chương 6: Mạch phát xung và tạo dạng xung Chương 7: Bộ nhớ bán dẫn Bài giảng Điện tử sốV1.0 31 Đại số Boole và các phương pháp biểu diễn hàm Bài giảng Điện tử sốV1.0 32 Đại số Boole Các định lý cơ bản: Các định luật cơ bản: Hoán vị: X.Y = Y.X, X + Y = Y + X Kết hợp: X.(Y.Z) = (X.Y).Z, X + (Y + Z) = (X + Y) + Z Phân phối: X.(Y + Z) = X.Y + X.Z, (X + Y).(X + Z) = X + Y.Z Định lý DeMorgan 7 Phủ định đúp6 X.(X + Y) = X X + X.Y = X Hấp thụ5 X + X = X X.X = X Bất biến4 Bù3 X + 1 = 1 X.0 = 0 Phần tử 0, 12 X + 0 = X X.1 = X Đồng nhất1 Dạng tổngDạng tíchTên gọiStt X = X X.Y.Z... X Y Z ... X Y Z ... X.Y.Z... X.X 0 X X 1 1 X Y Z Bài giảng Điện tử sốV1.0 33 Các phương pháp biểu diễn hàm Boole Có 3 phương pháp biểu diễn: Bảng trạng thái Bảng các nô (Karnaugh) Phương pháp đại số Bài giảng Điện tử sốV1.0 34 Phương pháp Bảng trạng thái Liệt kê giá trị (trạng thái) mỗi biến theo từng cột và giá trị hàm theo một cột riêng (thường là bên phải bảng). Bảng trạng thái còn được gọi là bảng sự thật hay bảng chân lý. Đối với hàm n biến sẽ có 2n tổ hợp độc lập. Các tổ hợp này được kí hiệu bằng chữ mi, với i = 0 ÷ 2n -1 và có tên gọi là các hạng tích hay còn gọi là mintex. Vì mỗi hạng tích có thể lấy 2 giá trị là 0 hoặc 1, nên nếu có n biến thì số hàm mà bảng trạng thái có thể thiết lập được sẽ là: 1111m7 0 1 0 1 0 1 0 C 011m6 001m5 001m4 010m3 010m2 000m1 000m0 fBAm n2N 2 Bài giảng Điện tử sốV1.0 35 Phương pháp Bảng Các nô (Karnaugh) Tổ chức của bảng Các nô: Các tổ hợp biến được viết theo một dòng (thường là phía trên) và một cột (thường là bên trái). Một hàm logic có n biến sẽ có 2n ô. Mỗi ô thể hiện một hạng tích hay một hạng tổng, các hạng tích trong hai ô kế cận chỉ khác nhau một biến. Tính tuần hoàn của bảng Các nô: Không những các ô kế cận khác nhau một biến mà các ô đầu dòng và cuối dòng, đầu cột và cuối cột cũng chỉ khác nhau một biến (kể cả 4 góc vuông của bảng). Bởi vậy các ô này cũng gọi là kế cận. Thiết lập bảng Các nô của một hàm: Dưới dạng chuẩn tổng các tích, ta chỉ việc ghi giá trị 1 vào các ô ứng với hạng tích có mặt trong biểu diễn, các ô còn lại sẽ lấy giá trị 0 (theo định lý DeMorgan). Dưới dạng tích các tổng, cách làm cũng tương tự, nhưng các ô ứng với hạng tổng có trong biểu diễn lại lấy giá trị 0 và các ô khác lấy giá trị 1. 1 0 A 10 B 01 11 1 0 A 1000 BC 11 01 01 11 10 00 AB 1000 CD Bài giảng Điện tử sốV1.0 36 Phương pháp đại số Có 2 dạng biểu diễn là dạng tuyển (tổng các tích) và dạng hội (tích các tổng). Dạng tuyển: Mỗi số hạng là một hạng tích hay mintex, thường kí hiệu bằng chữ "mi". Dạng hội: Mỗi thừa số là hạng tổng hay maxtex, thường được kí hiệu bằng chữ "Mi". Nếu trong tất cả mỗi hạng tích hay hạng tổng có đủ mặt các biến, thì dạng tổng các tích hay tích các tổng tương ứng được gọi là dạng chuẩn. Dạng chuẩn là duy nhất. Tổng quát, hàm logic n biến có thể biểu diễn chỉ bằng một dạng tổng các tích: hoặc bằng chỉ một dạng tích các tổng: ai chỉ lấy hai giá trị 0 hoặc 1. Đối với một hàm thì mintex và maxtex là bù của nhau. n2 1 n 1 0 i i i 0 f X ,...,X a m n2 1 n 1 0 i i i 0 f X ,...,X a m Bài giảng Điện tử sốV1.0 37 Các phương pháp rút gọn hàm Có 3 phương pháp rút gọn hàm: Phương pháp đại số Bảng trạng thái Phương pháp Quine Mc. Cluskey Bài giảng Điện tử sốV1.0 38 Phương pháp đại số Dựa vào các định lý đã học để đưa biểu thức về dạng tối giản. Ví dụ: Hãy đưa hàm logic về dạng tối giản: Áp dụng định lý , , ta có: Vậy nếu trong tổng các tích, xuất hiện một biến và đảo của biến đó trong hai số hạng khác nhau, các thừa số còn lại trong hai số hạng đó tạo thành thừa số của một số hạng thứ ba thì số hạng thứ ba đó là thừa và có thể bỏ đi. f AB AC BC A A 1 X XY X f AB AC BC A A AB ABC AC ABC AB AC Bài giảng Điện tử sốV1.0 39 Phương pháp đại số (tiếp) Ví dụ: Hãy đưa hàm logic về dạng tối giản: Áp dụng định lý , , ta có: f AB BCD AC BC A A 1 X XY X f AB BCD(A A) AC BC (AB ABCD) (ABCD AC) BC AB AC BC AB AB.C AB(1 C) AB.C AB C Bài giảng Điện tử sốV1.0 40 Phương pháp Bảng Các nô (Karnaugh) Phương pháp này thường được dùng để rút gọn các hàm có số biến không vượt quá 5. Các bước tối thiểu hóa: 1. Gộp các ô kế cận có giá trị ‘1’ (hoặc ‘0’) lại thành từng nhóm 2, 4, ...., 2i ô. Số ô trong mỗi nhóm càng lớn kết quả thu được càng tối giản. Một ô có thể được gộp nhiều lần trong các nhóm khác nhau. Nếu gộp theo các ô có giá trị ‘0’ ta sẽ thu được biểu thức bù của hàm. 2. Thay mỗi nhóm bằng một hạng tích mới, trong đó giữ lại các biến giống nhau theo dòng và cột. 3. Cộng các hạng tích mới lại, ta có hàm đã tối giản. Ví dụ: Hãy dùng bảng Các nô để giản ước hàm: Kết quả 111111 1101 01 1 1 11 110 100 AB 1000 CD f AB BCD AC BC f AB C f1 = AB f2 = C Bài giảng Điện tử sốV1.0 41 Phương pháp Quine Mc. Cluskey Phương pháp này có thể tối thiểu hóa được hàm nhiều biến và có thể tiến hành công việc nhờ máy tính. Các bước tối thiểu hóa: 1. Lập bảng liệt kê các hạng tích dưới dạng nhị phân theo từng nhóm với số bit 1 giống nhau và xếp chúng theo số bit 1 tăng dần. 2. Gộp 2 hạng tích của mỗi cặp nhóm chỉ khác nhau 1 bit để tạo các nhóm mới. Trong mỗi nhóm mới, giữ lại các biến giống nhau, biến bỏ đi thay bằng một dấu ngang (-). Lặp lại cho đến khi trong các nhóm tạo thành không còn khả năng gộp nữa. Mỗi lần rút gọn, ta đánh dấu # vào các hạng ghép cặp được. Các hạng không đánh dấu trong mỗi lần rút gọn sẽ được tập hợp lại để lựa chọn biểu thức tối giản. Ví dụ: f A,B,C,D 10, 11, 12, 13, 14, 15 Bài giảng Điện tử sốV1.0 42 Phương pháp Quine Mc. Cluskey (tiếp) Bước 1: Lập bảng Bước 2: Thực hiện nhóm các hạng tích 1 1 - - (12,13,14,15) 1 - 1 - (10,11,14,15) 1 0 1 - # (10,11) 1 - 1 0 # (10,14) 1 1 0 - # (12,13) 1 1 - 0 # (12,14) 1 - 1 1 # (11,15) 1 1 - 1 # (13,15) 1 1 1 - # (14,15) 1 0 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 10 12 11 13 14 15 Rút gọn lần thứ 2 (ABCD)Rút gọn lần 1 (ABCD)Nhị phân (ABCD)Hạng tích sắp xếp Bảng bBảng a x x x x xx xx 1 1 - - 1 - 1 - 151413121110A BCDTa nhận thấy rằng 4 cột có duy nhất một dấu "x" ứng với hai hạng 11-- và 1-1-. Do đó, biểu thức tối giản là: f A,B,C,D AB AC Bài giảng Điện tử sốV1.0 43 Cổng logic và các tham số chính Cổng logic cơ bản Một số cổng ghép thông dụng Logic dương và logic âm Các tham số chính Bài giảng Điện tử sốV1.0 44 Cổng logic cơ bản: AND, OR, NOT Cổng AND Cổng OR Cổng NOT Bài giảng Điện tử sốV1.0 45 Cổng AND Hàm ra của cổng AND 2 và nhiều biến vào như sau: HHH111 Theo mức logicTheo giá trị logic Bảng trạng thái cổng AND 2 lối vào L H L B H L L A L001 L010 L000 ffBA f f (A, B) AB; f f (A, B,C, D,...) A.B.C.D... A B A B C f f &0 0 0 &0 0 0 0 A B A B C f f Ký hiệu cổng AND Chuẩn ANSI Chuẩn IEEE 1 1 Lối vào A Lối ra f t t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 Lối vào B 11 1 1 00000000 0 0 0 0 0 01 1 0 1 1 10 0 0 0 Đồ thị dạng xung vào, ra của cổng AND Bài giảng Điện tử sốV1.0 46 Cổng OR Hàm ra của cổng OR 2 và nhiều biến vào như sau: f f (A, B) A B; f f (A, B,C, D,...) A B C D ... A B A B C f f >=10 0 0 >=10 0 0 0 A B A B C f f Ký hiệu cổng OR Chuẩn ANSI Chuẩn IEEE HHH111 Theo mức logicTheo giá trị logic Bảng trạng thái cổng OR 2 lối vào L H L B H L L A H101 H110 L000 ffBA fB t t0 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 0 1 1 0 0 0 1 1 1 0 A 0 0 1 1 1 0 0 1 0 0 0 1 1 1 1 0 1 1 1 0 Đồ thị dạng xung của cổng OR. Bài giảng Điện tử sốV1.0 47 Cổng NOT Hàm ra của cổng NOT: Theo mức logicTheo giá trị logic Bảng trạng thái cổng NOT H L A L01 H10 ffA f A A A Dạng xung ra Bài giảng Điện tử sốV1.0 48 Một số cổng ghép thông dụng Cổng NAND Cổng NOR Cổng khác dấu (XOR) Cổng đồng dấu (XNOR) Bài giảng Điện tử sốV1.0 49 Cổng NAND Ghép nối tiếp một cổng AND với một cổng NOT ta được cổng NAND. Hàm ra của cổng NAND 2 và nhiều biến vào như sau: f AB f ABCD... A B A B C f f &0 0 0 &0 0 0 0 A B A B C f f Ký hiệu cổng NAND Chuẩn ANSI Chuẩn IEEE LHH011 Theo mức logicTheo giá trị logic Bảng trạng thái cổng NAND 2 lối vào L H L B H L L A H101 H110 H100 ffBA Bài giảng Điện tử sốV1.0 50 Cổng NOR Ghép nối tiếp một cổng OR với một cổng NOT ta được cổng NOR. Hàm ra của cổng NOR 2 và nhiều biến vào như sau: f A B f A B C D ... A B A B C f f >=10 0 0 >=10 0 0 0 A B A B C f f Ký hiệu cổng NOR Chuẩn ANSI Chuẩn IEEE LHH011 Theo mức logicTheo giá trị logic Bảng trạng thái cổng NOR 2 lối vào L H L B H L L A L001 L010 H100 ffBA Bài giảng Điện tử sốV1.0 51 Cổng NAND Ghép nối tiếp một cổng AND với một cổng NOT ta được cổng NAND. Hàm ra của cổng NAND 2 và nhiều biến vào như sau: f AB f ABCD... A B A B C f f &0 0 0 &0 0 0 0 A B A B C f f Ký hiệu cổng NAND Chuẩn ANSI Chuẩn IEEE LHH011 Theo mức logicTheo giá trị logic Bảng trạng thái cổng NAND 2 lối vào L H L B H L L A H101 H110 H100 ffBA Bài giảng Điện tử sốV1.0 52 Cổng NOR Ghép nối tiếp một cổng OR với một cổng NOT ta được cổng NOR. Hàm ra của cổng NOR 2 và nhiều biến vào như sau: f A B f A B C D ... A B A B C f f >=10 0 0 >=10 0 0 0 A B A B C f f Ký hiệu cổng NOR Chuẩn ANSI Chuẩn IEEE LHH011 Theo mức logicTheo giá trị logic Bảng trạng thái cổng NOR 2 lối vào L H L B H L L A L001 L010 H100 ffBA Bài giảng Điện tử sốV1.0 53 Cổng XOR - cổng khác dấu Cổng XOR còn gọi là cổng khác dấu, hay cộng modul 2. Hàm ra của cổng XOR 2 biến vào như sau: f AB AB hay f A B A B A B C f f =10 0 0 =10 0 0 0 A B A B C f f Ký hiệu cổng XOR Chuẩn ANSI Chuẩn IEEE LHH011 Theo mức logicTheo giá trị logic Bảng trạng thái cổng XOR 2 lối vào L H L B H L L A H101 H110 L000 ffBA Bài giảng Điện tử sốV1.0 54 Cổng XNOR - cổng đồng dấu Cổng XNOR còn gọi là cổng đồng dấu. Hàm ra của cổng XNOR 2 biến vào như sau: f AB AB hay f A B A B : A B A B C f f =0 0 0 =0 0 0 0 A B A B C f f Ký hiệu cổng XNOR Chuẩn ANSI Chuẩn IEEE HHH111 Theo mức logicTheo giá trị logic Bảng trạng thái cổng XNOR 2 lối vào L H L B H L L A L001 L010 H100 ffBA Bài giảng Điện tử sốV1.0 55 Logic dương và logic âm Logic dương là logic có điện thế mức cao H luôn lớn hơn điện thế mức thấp L (VH > VL). Logic âm là đảo của logic dương (VH < VL). Khái niệm logic âm thường được dùng để biểu diễn trị các biến. Logic âm và mức âm của logic là hoàn toàn khác nhau. 0 1 1 0 0 1 0 1 1 1 0 0 1 0 0 t V H L 0 1 1 0 0 1 0 1 1 1 0 0 1 0 t V H L 0 a) Logic dương với mức dương. b) Logic dương với mức âm. Bài giảng Điện tử sốV1.0 56 Các tham số chính Mức logic Độ chống nhiễu Hệ số ghép tải K Công suất tiêu thụ Trễ truyền lan Bài giảng Điện tử sốV1.0 57 Mức logic Họ TTL Họ CMOS Mức logic là mức điện thế trên đầu vào và đầu ra của cổng tương ứng với logic "1" và logic "0", nó phụ thuộc điện thế nguồn nuôi của cổng (VCC đối với họ TTL (Transistor Transistor Logic) và VDD đối với họ MOS (Metal Oxide Semiconductor)). Lưu ý: mức logic vào vượt quá điện thế nguồn nuôi có thể gây hư hỏng cho cổng. 5v 4v 3v 2v 1v 0v VVHmax VVHmin VVLmax0,8v VRHmax VVHmax VRHmax VRHmin VRLmax VVHmin VVLmax VRHmin VRLmax 2,4v 0,4v 3,5v 1,5v 4,9v 0,1v NL NH NL NH Bài giảng Điện tử sốV1.0 58 Độ chống nhiễu Độ chống nhiễu (hay độ phòng vệ nhiễu) là mức nhiễu lớn nhất tác động tới lối vào hoặc lối ra của cổng mà chưa làm thay đổi trạng thái vốn có của nó. a) Tác động nhiễu khi mức ra cao b) Tác động nhiễu khi mức ra thấp Ảnh hưởng của nhiễu có thể phân ra hai trường hợp: TTL TTL Cổng I Cổng II VRH VVL VVH VNH TTL TTL Cổng I Cổng II VVH VRH VRL VVL VNL RHmin NH VHmin NH VHmin RHminV V V V V V NLV 2V 2,4V 0,4V NLV 3,5V 4,9V 1, 4V RLmax NL VLmax NL VLmax RLmaxV V V V V V NLV 0,8V 0, 4V 0, 4V NLV 1,5V 0,1V 1, 4V + Nhiễu mức cao: đầu ra cổng I lấy logic H (hình a), đầu ra cổng II là logic L, nếu các cổng vẫn hoạt động bình thường. Khi tính tới tác động của nhiễu: + Nhiễu mức thấp: đầu ra cổng I lấy logic L (hình b), tương tự ta có: Với cổng TTL: Với cổng CMOS: Với cổng TTL: Với cổng CMOS: Bài giảng Điện tử sốV1.0 59 Hệ số ghép tải K Cho biết khả năng nối được bao nhiêu lối vào tới đầu ra của 1 cổng đã cho. Hệ số ghép tải phụ thuộc dòng ra (hay dòng phun) của cổng chịu tải và dòng vào (hay dòng hút) của các cổng tải ở cả hai trạng thái H, L. a) Mức ra của cổng chịu tải là H b) Mức ra của cổng chịu tải là L Công thức tính hệ số ghép tải: ; IRL=1,6mA gọi là đơn vị ghép tải (Dt) A B Cổng chịu tải A B Các cổng tải H L IRH IRL Cổng chịu tải Các cổng tải maxRL t RL IK I Bài giảng Điện tử sốV1.0 60 Công suất tiêu thụ Hai trạng thái tiêu thụ dòng của cổng logic ICCH - Là dòng tiêu thụ khi đầu ra lấy mức H, ICCL - Là dòng tiêu thụ khi đầu ra lấy mức L. Theo thống kê, tín hiệu số có tỷ lệ bit H / bit L khoảng 50%. Do đó, dòng tiêu thụ trung bình ICC được tính theo công thức: ICC = (ICCH + ICCL)/ 2 Công suất tiêu thụ trung bình của mỗi cổng sẽ là: P0 = ICC . VCC H +Vcc ICCH L H L +Vcc ICCL H H Bài giảng Điện tử sốV1.0 61 Trễ truyền lan Tín hiệu đi qua một cổng phải mất một khoảng thời gian, được gọi là trễ truyền lan. Trễ truyền lan xảy ra tại cả hai sườn của xung ra. Nếu kí hiệu trễ truyền lan ứng với sườn trước là tTHL và sườn sau là tTLH thì trễ truyền lan trung bình là: tTbtb = (t THL + tTLH)/2 Thời gian trễ truyền lan hạn chế tần số công tác của cổng. Trễ càng lớn thì tần số công tác cực đại càng thấp. Vào Ra Vào Ra tTHL tTLH
File đính kèm:
 bai_giang_dien_tu_so_chuong_2_dai_so_boole_va_cac_phuong_pha.pdf
bai_giang_dien_tu_so_chuong_2_dai_so_boole_va_cac_phuong_pha.pdf

