Bài giảng Biến đổi năng lượng điện cơ - Chương 4: Giải tích hệ thống điện cơ dùng các phương pháp năng lượng
Mạch từ với một bộ phận dịch chuyển được khảo sát trong phần
này.
Tìm ra các mô hình toán học của hệ thống điện cơ.
Một hay nhiều cuộn dây tương tác với nhau tạo ra lực hay moment
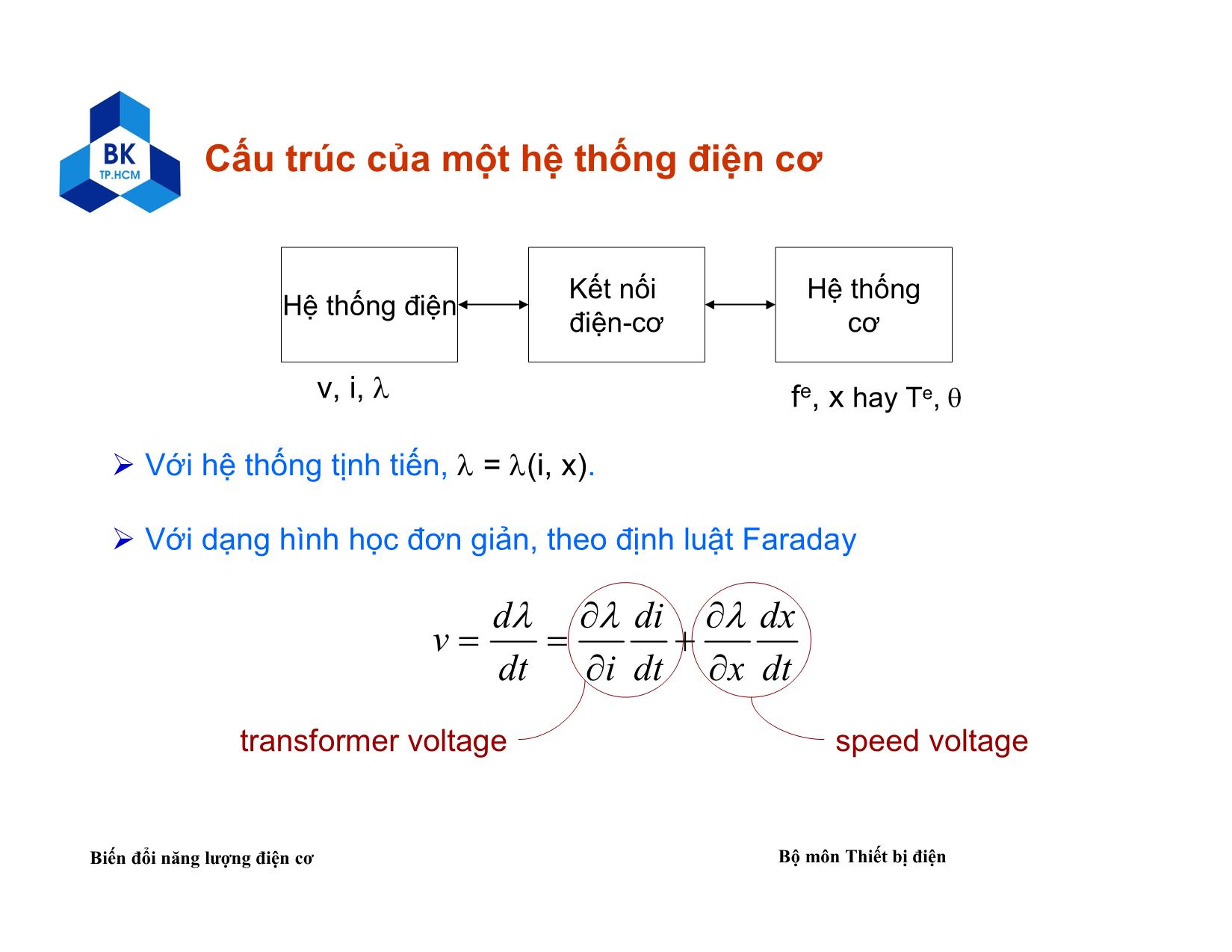
của hệ thống cơ.
Nói chung, cả dòng điện trong cuộn dây và lực (moment) đều thay
đổi theo thời gian.
Tập hợp phương trình vi phân điện cơ được đưa ra và được đưa về
dạng phương trình trạng thái để thuận tiện cho việc mô phỏng, phân
tích và thiết kế.
Lực từ fe = fe(i, x) = fe(, x) (vì i được tính từ = (i, x)) của hệ thống
có một cửa điện và 1 cửa cơ.
fe có chiều theo chiều dương của x.
Xét hệ thống trong hình Fig. 4.17, tương đương với Fig. 4.18. Gọi Wm
là năng lượng dự trữ, theo định luật bảo toàn năng lượng

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Biến đổi năng lượng điện cơ - Chương 4: Giải tích hệ thống điện cơ dùng các phương pháp năng lượng

Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Biến đổi năng lượng điện cơ -Hệ thống điện cơ Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Mạch từ với một bộ phận dịch chuyển được khảo sát trong phần này. Tìm ra các mô hình toán học của hệ thống điện cơ. Một hay nhiều cuộn dây tương tác với nhau tạo ra lực hay moment của hệ thống cơ. Nói chung, cả dòng điện trong cuộn dây và lực (moment) đều thay đổi theo thời gian. Tập hợp phương trình vi phân điện cơ được đưa ra và được đưa về dạng phương trình trạng thái để thuận tiện cho việc mô phỏng, phân tích và thiết kế. Hệ thống điện cơ – Giới thiệu Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện S Xét hệ thống như hình Fig. 4.1 Định luật vòng Ampere trở thành Định luật Faraday Hệ thống tịnh tiến – Ứng dụng của các luật về điện từ S fC daJdlH NiHl C S daBdt d dlE dt d N dt d v trở thành Ứng dụng của định luật Gauss phụ thuộc vào hình dạng hình học và cho hệ thống có H khác nhau. Định luật bảo tòan điện tích dẫn tới các định luật Kirchhoff KCL. Đường kín C Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Với hệ thống tịnh tiến, = (i, x). Với dạng hình học đơn giản, theo định luật Faraday Cấu trúc của một hệ thống điện cơ Hệ thống điện Kết nối điện-cơ Hệ thống cơ v, i, fe, x hay Te, dt dx xdt di idt d v transformer voltage speed voltage Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Vì vậy, ixL dt dx dx xdL i dt di xLv Với hệ thống không có phần dịch chuyển Li dt di Lv và Với hệ thống nhiều cửa M j j j kN j j j kk k dt dx xdt di idt d v 11 Nk ,...,2,1 Lực và từ thông móc vòng có thể là hàm của tất cả các biến. Hệ thống (điện) tuyến tính Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Tìm H1, H2, , và v, với giả thiết sau: 1) = , 2) g >> w, x >> 2w và 3) bỏ qua từ thông rò. 022 2010 wdHwdH xg Ni HH 21Đưa đến Định luật Gauss xg iNwd N 2 02 Từ thông móc vòng Độ tự cảm xg Nwd xL 2 02 dt dx xg iNwd dt di xg Nwd tv 2 2 0 2 0 22 Điện áp Ví dụ 4.1 Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện VD. 4.2: Hình Fig. 4.7. Tìm s, r dưới dạng hàm của is, ir, và , và tìm vs va vr của rotor dạng trụ. Giả sử = , và g << R và l. 31 r rrss r H g iNiN H 42 r rrss r H g iNiN H lRHNlRHNN rsrssss 2010 Đơn giản thành rrssss iLNNiLN 2 100 2 Tương tự, rrsrsr iLNiLNN 0 2 0 2 1 0 0 dt d Mi dt di M dt di Ltv r rs ss sincos Với máy thực tế, Các hệ thống quay Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Tính 1 và 2 và xác định độ tự cảm và hỗ cảm cho hệ thống hình Fig. 4.14, sử dụng mạch tương đương. Rx Rx Rx N2i2N1i1 1 2 2 00 W x A x Rx 2111 2 xx RRiN 2122 2 xx RRiN 221121 2 0 111 2 3 iNNiN x W N 222121 2 0 222 2 3 iNiNN x W N Xác định độ tự cảm và hỗ cảm? Ví dụ 4.4 Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Lực từ fe = fe(i, x) = fe(, x) (vì i được tính từ = (i, x)) của hệ thống có một cửa điện và 1 cửa cơ. fe có chiều theo chiều dương của x. Xét hệ thống trong hình Fig. 4.17, tương đương với Fig. 4.18. Gọi Wm là năng lượng dự trữ, theo định luật bảo toàn năng lượng Tốc độ thay đổi năng lượng dự trữ Công suất điện vào Công suất cơ ra = _ dt dx f dt d i dt dx fvi dt dW eem dxfiddW em hay Một biến số điện và một biến số cơ có thể được chọn một cách độc lập, mà không thay đổi bản chất vật lý của đối tượng. Giả sử (, x) được chọn. Tính lực từ dùng pp năng lượng Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Sự thay đổi của năng lượng dự trữ khi đi từ a tới b – x độc lập với đường tích phân (Fig. 4.19). Với đường A b a b a dxidxxfxWxW b x x a e aambbm ,,,, Đường B b a b a x x b e aaambbm dxxfdxixWxW ,,,, Cả hai cách đều phải cho ra cùng kết quả. Nếu a = 0, thì lực từ bằng 0, vì thế đường A dễ dàng hơn b dxixWxW bambbm 0 ,,0, Tổng quát 0 ,, dxixWm Tính lực từ dùng pp năng lượng (tt) Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Ta có dxfiddW em Vì Wm = Wm(, x), vi phân của Wm được tính dx x xW d xW dt dW mmm ,, So sánh 2 phương trình, ta được xW i m , x xW f me , Quan hệ lực - năng lượng Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Tính fe(, x) và fe(i, x) của hệ thống trong hình VD. 4.1 gx i L gx i g Nwd xg iNwd N 11 22 0 2 0 2 0 gx L i 1 0 gx L dgx L dxiWm 12 1, 0 2 0 0 0 gL x x W f me 0 2 2 , 2 2 0 2 0 22 0 12 1 12 , gx iL gxgL iL xif e Giải được i Tính fe Ví dụ 4.5 Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Để tính Wm(, x), cần tính i = i(, x). Tuy nhiên việc này khá phức tạp, nên việc tính fe trực tiếp từ = (i, x) sẽ thuận tiện hơn. dxfiddW em diidid diidid dxfdiiddW em dxfdiWid e m Định nghĩa của đồng năng lượng xiWWWi mmm , '' Tích phân dW’m dọc theo đường Ob’b (Fig. 4.21), f e = 0 dọc theo Ob’ i m dixixiW 0 ' ,, dx x W di i W dW mmm '' ' Ta có, fe Tính lực từ dùng pp ‘đồng năng lượng’ Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Tìm fe trong hệ thống hình Fig. 4.22. Ni Riron Rgap A l R ciron A x Rgap 0 2 xR NiNi RR Ni A x A l gapiron c 0 2 xR iN N 2 xR iN dixiW i m 2 , 22 0 ' 220 2222' 0 1 2 A x A l me cA iN xRdx diN x W f Từ thông móc vòng và đồng năng lượng Lực từ Ví dụ 4.8 Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Xét hệ thống điện tuyến tính trong hình Fig. 4.24, A Area , 0 dxiWm B Area , 0 ' i m dixiW Nếu (i, x) là hàm phi tuyến như hình Fig. 4.25, thì 2 diện tích sẽ không bằng nhau. Tuy nhiên, fe được tính từ năng lượng hay đồng năng lượng sẽ bằng nhau. Đầu tiên, giữ không đổi, năng lượng Wm giảm một lượng – Wm như trong hình Fig. 4.26(a) ứng với một lượng tăng x. Sau đó, giữ i không đổi, đồng năng lượng tăng W’m. Lực từ trong cả hai trường hợp x W f m x e 0 lim x W f m x e ' 0 lim Năng lượng và đồng năng lượng biểu diễn bằng đồ thị Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Xét hệ thống có 2 cửa điện và 1 cửa cơ, với 1 = 1(i1, i2, x) và 2 = 2(i1, i2, x). Tốc độ thay đổi năng lượng dự trữ dt dx f dt d i dt d i dt dx fiviv dt dW eem 22 1 12211 dxfdididW em 2211 hay 221122112211 didiiiddidi dxfdidiWiid em 22112211 dxfdididW em 2211 ' Xét nên, ' mW 21 0 ' 2 ' 212 0 ' 1 ' 1121 ' ,,,0,,, ii m dixiidixixiiW Cuối cùng, Đồng năng lượng cho hệ thống 2 cửa điện và 1 cửa cơ Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Xét một hệ thống với N cửa điện và M cửa cơ, từ thông móc vòng là 1(i1, ..., iN, x1, ..., xM), ..., N(i1, ..., iN, x1, ..., xM). M e M e NNm dxfdxfididdW ...... 1111 NNNNNN didiididiid ......... 111111 M i i e i N i ii W m N i ii dxfdiWid m 111 ' Ni i W i m i ,...,1 ' Mi x W f i me i ,...,1 ' Lực từ trong hệ thống nhiều cửa Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Để W’m, đầu tiên tính tích phân dọc theo các trục xi axes, sau đó theo mỗi trục ii. Khi lấy tích phân dọc theo xi, W’m = 0 vì f e bằng zero. Vì thế, ' 21 ' 121 0 ' 221 ' 212 0 ' 121 ' 11 ' ,...,,,,...,, ...,...,,0,...,, ,...,,0,...,0, 2 1 NMNNN i M i Mm dixxxiiii dixxxii dixxxiW Chú ý rằng với trường hợp đặc biệt hệ thống 2 cửa điện 2 cửa cơ, 21 0 ' 221 ' 212 0 ' 121 ' 11 ' ,,,,,0, ii m dixxiidixxiW Và, 1 ' 1 dx W f me 2 ' 2 dx W f me Tính tóan W’m Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Tính W’m và các moment từ của hệ thống 3 cửa điện và 1 cửa cơ. cos31111 MiiL sin32222 MiiL sincos 213333 MiMiiL sincos 2 1 2 1 2 1 ,,,,,,0,,,,0,0, 3231 2 333 2 222 2 111 0 ' 3 ' 32130 ' 2 ' 2120 ' 1 ' 11 ' 321 iMiiMiiLiLiL diiiidiiidiiW iii m cossin 3231 ' iMiiMi W T me cossin 3231 ' iMiiMi W T me Ví dụ 4.10 Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Bỏ qua tổn hao từ, mối quan hệ đơn giản của hệ thống điện cơ có thể nhận được là, dt d i vf e eT dt dWm Ta có x xW f me , xW i m , Chú ý rằng x W x W mm 22 Điều kiện cần và đủ để bảo toàn là xf x xi e ,, i xif x xi e ,, hay Sự bảo tòan năng lượng Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Với hệ thống này Điều kiện bảo toàn 1 ' 1 i Wm dxfdididW em 2211 ' Các phương trình từ thông móc vòng và lực từ là 2 ' 2 i Wm x W f me ' 1 1 i f x e 2 2 i f x e 1 2 2 1 ii Có thể mở rộng cho hệ thống nhiều cửa điện - cơ. Hệ thống 2 cửa điện và 1 cửa cơ Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Ta có dxxfdxidW em ,, Khi đi từ a tới b trong hình Fig. 4.31, sự thay đổi năng lượng dự trữ là b a b a x x e aambbm dxfidxWxW ,, bababam EFMEFEW Trong đó EFE là năng lượng từ nguồn điện và EFM là năng lượng từ nguồn cơ. Để xác định EFE và EFM, cần xác định một đường đi cụ thể. Khái niệm EFM dùng để khảo sát sự chuyển đổi năng lượng trong các thiết bị hoạt động theo chu kì. Bảo toàn năng lượng giữa 2 điểm Biến đổi năng lượng điện cơ Bộ môn Thiết bị điện Sau một chu kỳ, khi hệ thống trở lại trạng thái ban đầu, dWm = 0. dxfiddxfid ee 0 Từ hình 4.30, id = EFE, và –fedx = EFM. Vì vậy, sau một chu kỳ, 0EFMEFE 0 cyclecycle EFMEFE Có thể tính EFE hoặc EFM sau một chu kỳ. Nếu EFE|cycle > 0, hệ thống hoạt động như một động cơ, và EFM|cycle < 0. Nếu EFE|cycle < 0, hệ thống hoạt động như máy phát, và EFM|cycle > 0. VD. 4.14 – 4.16 Bảo toàn năng lượng sau một chu kỳ
File đính kèm:
 bai_giang_bien_doi_nang_luong_dien_co_chuong_4_giai_tich_he.pdf
bai_giang_bien_doi_nang_luong_dien_co_chuong_4_giai_tich_he.pdf

