Bài giảng An toàn và An ninh thông tin - Chương II: Các phương pháp mã hóa đối xứng - Nguyễn Linh Giang

An toàn và An ninh thông tin
Nguyễn Linh Giang
Bộ môn Truyền thông
và Mạng máy tính
I. Nhập môn An toàn thông tin 
II. Các phương pháp mã hóa đối xứng
III. Các hệ mật khóa công khai
IV. Xác thực thông điệp
V. Chữ ký số và các giao thức xác thực
VI. Đánh dấu ẩn vào dữ liệu
Chương II. 
Các phương pháp mã hóa đối xứng
1. Sơ đồ chung của phương pháp mã hóa
đối xứng
2. Một số phương pháp mã hóa đối xứng
kinh điển
3. Phương pháp DES
4. Quản trị và phân phối khóa
z Giả thiết
– Thuật toán mã hóa phải đủ mạnh để không thể giải
mã được thông điệp nếu chỉ dựa trên duy nhất nội
dung của văn bản được mã hóa( ciphertext ).
– Sự an toàn của phương pháp mã hóa đối xứng chỉ
phụ thuộc vào độ bí mật của khóa mà không phụ
thuộc vào độ bí mật của thuật toán.
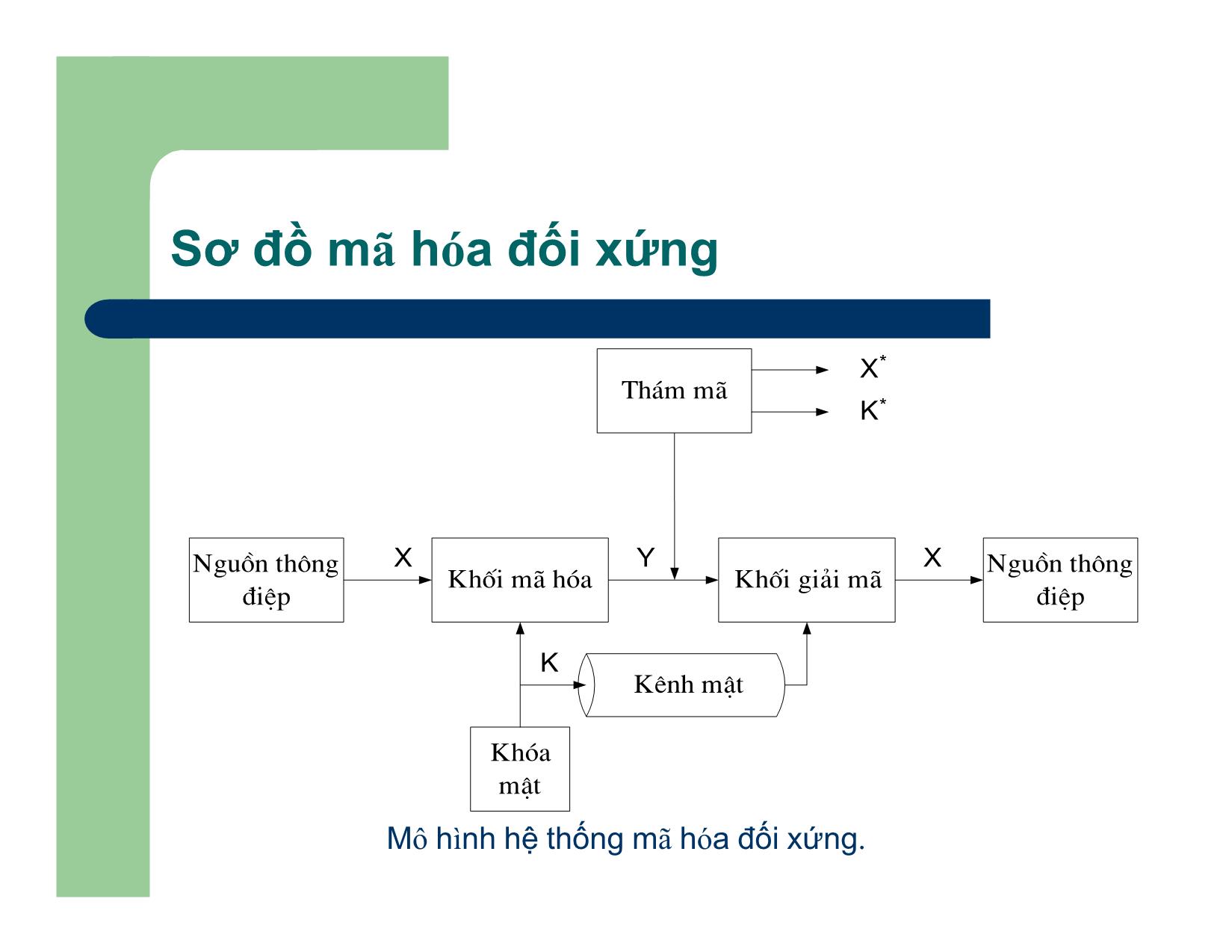
Sơ đồ mã hóa đối xứng
Mô hình hệ thống mã hóa đối xứng.
Nguån th«ng
®iÖp
Khèi m· hãa Khèi gi¶i m·
Nguån th«ng
®iÖp
Khãa
mËt
Th¸m m·
Kªnh mËt
X Y X
K
X*
K*
Sơ đồ mã hóa đối xứng
z Nguồn thông tin: 
– Tập hợp thông điệp của nguồn: 
Các xâu ký tự X = { X1, X2, ..., XM };
– Thông điệp: xâu ký tự độ dài m: 
Xi = [ xi1, xi2, ..., xim ]
xik∈ A; A – bảng ký tự nguồn; thông thường A= {0, 1}
– Mỗi thông điệp Xi có một xác suất xuất hiện P( X = Xi )
Sơ đồ chung của phương pháp mã hóa
đối xứng
z Khóa mật mã
– Tập hợp khoá K = { K1, K2, ... KL},
– Khóa độ dài l: Ki=[ki1, ..., kil];
kij ∈ C, C - bảng ký tự khóa; thông thường C 
= {0, 1}
Sơ đồ chung của phương pháp mã
hóa đối xứng
z Mã mật:
– Tập hợp thông điệp mã mật Y = [ Y1, Y2, ..., YN ]
– Thông điệp mã mật: Yj = [yj1, yj2, ..., yjn]
– yjp∈B, B – bảng ký tự mã mật; thông thường B = {0, 1}
Sơ đồ chung của phương pháp mã
hóa đối xứng
z Quá trình mã hóa và giải mã:
– Quá trình mã hóa:
Y = EK( X )
– Quá trình giải mã:
z Bên nhận giải mã thông điệp bằng khóa được phân phối:
X = DK( Y ) = DK ( EK,R( X ) )
Sơ đồ chung của phương pháp mã
hóa đối xứng
z Phía tấn công
– Vấn đề đặt ra: đối phương nhận được thông điệp
Y, nhưng không có được khóa K. Dựa vào thông
điệp Y, đối phương phải khôi phục lại hoặc K, 
hoặc X hoặc cả hai.
Sơ đồ chung của phương pháp mã
hóa đối xứng
z Mật mã
– Phân loại các hệ thống mật mã
z Dạng của phép toán tham gia vào mã hóa văn bản từ dạng
thông thường sang dạng được mật mã hóa;
z Số lượng khóa được dùng trong thuật toán.
– Hệ thống mã hóa đối xứng.
– Hệ thống mã hóa không đối xứng.
z Phương thức mà văn bản ban đầu được xử lý:
– Mã hóa khối;
– Mã hóa dòng.
Sơ đồ chung của phương pháp mã hóa
đối xứng
z Thám mã
– Chỉ biết văn bản được mã hoá;
– Biết một số văn bản gốc và mật mã tương ứng;
– Tấn công bằng văn bản rõ được lựa chọn trước;
– Tấn công bằng mật mã cho trước;
– Tấn công bằng bản rõ tùy chọn.
Sơ đồ chung của phương pháp mã
hóa đối xứng
zSơ đồ mã hóa được coi là an toàn vô điều kiện
– Văn bản mã mật không chứa đủ thông tin để xác đinh
duy nhất văn bản gốc tương ứng;
zSơ đồ mã mật được coi là an toàn theo tính
toán
– Giá thành tấn công vượt quá giá trị của thông tin mật;
– Thời gian giải mật vượt quá thời hạn giữ mật của thông
tin. 
Sơ đồ chung của phương pháp mã
hóa đối xứng
– Ví dụ: thuật toán DES ( Data Encryption Standard ): Khoá nhị phân
• Độ dài 32 bit ⇒Số lượng khoá: 232 ⇒ 35.8 phút xử lý với tốc độ
1 phép mã hoá/μs ⇒ 2.15 ms với tốc độ 106 phép mã hoá / μs.
• Độ dài 56 bit ⇒Số lượng khoá: 256 ⇒ 1142 năm xử lý với tốc
độ 1 phép mã hoá/μs ⇒ 10.01 giờ với tốc độ 106 phép mã hoá / 
μs.
• Độ dài 128 bit ⇒Số lượng khoá: 2128 ⇒ 5.4 x 1024 năm xử lý với
tốc độ 1 phép mã hoá/μs ⇒ 5.4 x 1018 năm với tốc độ 106 phép
mã hoá / μs.
Sơ đồ chung của phương pháp mã
hóa đối xứng
z Các phương pháp thay thế
– Mã Caesar
z Các ký tự chữ cái được gán giá trị ( a = 1, b = 2, ... )
C = E( p ) = ( p + k ) mod ( 26 )
Trong đó k = 1 .. 25.
z k là khoá mật mã.
z Quá trình giải mã:
p = D( C ) = ( C – k ) mod ( 26 )
Một số phương pháp mã hóa đối
xứng kinh điển
z Các vấn đề của mã Caesar:
– Thuật toán mã hoá và giải mã đã biết trước.
– Thám mã:
z Không gian khóa nhỏ: chỉ có 25 khoá;
z Khi thám mã bằng phương pháp vét cạn: chỉ cần thử
với 25 khóa;
– Ngôn ngữ trong bản gốc đã biết trước và dễ dàng nhận
biết.
Một số phương pháp mã hóa đối
xứng kinh điển
– Mã mật Hill
z Thuật toán mã hoá
– Mỗi ký tự được gán giá trị số: a = 0, b = 1, ..., z = 25
– Lựa chọn m ký tự liên tiếp của văn bản gốc;
– Thay thế các ký tự đã lựa chọn bằng m ký tự mã mật, 
được tính bằng m phương trình tuyến tính.
– Hệ phương trình mã hóa:
C = KP ( mod 26 )
K- ma trận khóa
z Thuật toán giải mã
P = K-1C ( mod 26 )
Một số phương pháp mã hóa đối
xứng kinh điển
– Ví dụ: với m = 3, hệ các phương trình tuyến tính có dạng
sau:
C1 = ( k11p1 + k12p2 + k13p3 ) mod 26
C2 = ( k21p1 + k22p2 + k23p3 ) mod 26
C3 = ( k31p1 + k32p2 + k33p3 ) mod 26
C = KP
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
=
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
3
2
1
333231
232221
131211
3
2
1
p
p
p
kkk
kkk
kkk
C
C
C
Một số phương pháp mã hóa đối
xứng kinh điển
– Ma trận K là ma trận khoá mật mã
– Ví dụ: với ma trận K bằng:
Xâu ký tự: “paymoremoney” sẽ được mã hoá thành
“LNSHDLEWMTRW”
“pay” ⇔ (15, 0, 24 ); K( 15, 0, 24 )T mod 26 = ( 11, 13, 18) ⇔ “LNS”
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
=
1922
211821
51717
K
Một số phương pháp mã hóa đối
xứng kinh điển
– Giải mã thông điệp bằng ma trận K-1.
– Hệ mã Hill:
– Các phép toán thực hiện theo modulo 26
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
=
17024
61715
1594
K 1-
⎩⎨
⎧
====
==
−− PKPKCK(C)DP
KP(P)EC
11
K
K
Một số phương pháp mã hóa đối
xứng kinh điển
z Mức độ an toàn của hệ mã Hill
– Mã mật Hill có tính mật cao khi phía tấn công chỉ có văn bản
mật. 
– Thám mã hệ mã Hill: dễ dàng bị bẻ khóa nếu bên tấn công biết
được văn bản rõ và văn bản mật tương ứng ( known plaintext
attack )
z Hệ mã mật Hill m x m;
z Thám mã đã có m cặp văn bản gốc – văn bản mật, mỗi
văn bản có độ dài m; 
z Tạo các cặp: Pj = ( p1j, p2j, ..., pmj ) và Cj = ( C1j, C2j, ..., Cmj ) 
sao cho Cj = KPj với 1≤ j ≤ m đối với một khoá K chưa
biết.
z Xác định hai ma trận m x m, X = ( pij ) và Y = ( Cij )
Một số phương pháp mã hóa đối
xứng kinh điển
– Ta có Y = XK ⇒ K = X-1Y.
– Ví dụ: văn bản gốc: “friday” được mã hoá bằng mã mật
Hill 2 x 2 thành “PQCFKU”.
z Ta có: K( 5 17 ) = ( 15 16 ); K( 8 3 ) = ( 2 5 ); K( 0 24 ) = ( 10
20 )
z Với hai cặp ban đầu ta có :
⎟⎟⎠
⎞
⎜⎜⎝
⎛=⎟⎟⎠
⎞
⎜⎜⎝
⎛
⎟⎟⎠
⎞
⎜⎜⎝
⎛=⎟⎟⎠
⎞
⎜⎜⎝
⎛
⎟⎟⎠
⎞
⎜⎜⎝
⎛=
⇒⎟⎟⎠
⎞
⎜⎜⎝
⎛=⎟⎟⎠
⎞
⎜⎜⎝
⎛
−
38
197
52
1615
152
19
52
1615
38
175
K
K
38
175
52
1615
1
Một số phương pháp mã hóa đối
xứng kinh điển
– Hệ thống Vernam.
z Để chống lại quá trình thám mã, cần lựa chọn khoá thoả mãn:
– Khoá có độ dài bằng văn bản rõ.
– Khóa được chọn sao cho khoá và văn bản gốc độc lập thống kê.
z Hệ mã mật Vernam: 
– Dùng cho mã nhị phân
– Ci = pi ⊕ ki
– pi: bit thứ i của văn bản gốc;
– ki: bit thứ i của khoá;
– Ci: bit thứ i của văn bản được mã hoá;
– ⊕: phép toán XOR.
Một số phương pháp mã hóa đối
xứng kinh điển
z Giải mã bằng phép toán ngược: pi = Ci ⊕ ki
z Tạo khoá: tạo vòng lặp với một khoá. Như vậy thực tế, hệ
thống làm việc với một khóa rất dài nhưng lặp lại.
z Hệ thống Vernam có thể bị phá nếu đối phương biết một
văn bản mã có độ dài đủ lớn, sử dụng một số văn bản
gốc đã biết.
z Với khoá được sinh ngẫu nhiên, có độ dài bằng độ dài
văn bản gốc, không lặp lại: sơ đồ mã sử dụng một lần ( 
one-time pad ): không thể phá khoá. Đầu ra độc lập thống
kê với văn bản gốc.
z Vấn đề nảy sinh: đảm bảo mật cho quá trình gửi và nhận
khoá ngẫu nhiên.
Một số phương pháp mã hóa đối
xứng kinh điển
Mã hóa khối ( block cipher )
z Định nghĩa
– Mã khối là mật mã khóa đối xứng thực hiện trên 
nhóm bit có độ dài cố định. Nhóm bit này được gọi 
là một khối. Quá trình chuyển đổi không thay đổi.
– Khi mã hóa, mã khối có thể thực hiện trên từng khối 
độ dài 128 bit của bản rõ tại đầu vào thứ nhất và cho 
ra khối 128 bit của mã mật.
z Quá trình biến đổi được kiểm soát bằng đầu vào thứ hai:
khóa mật
– Quá trình giải mã thực hiện tương tự: nhận tại đầu 
vào thứ nhất khối 128 bit của mật mã, khóa mật và
tại đầu ra ta nhận được khối 128 bit của bản rõ
– Để mã hóa bản tin có độ dài lớnhơn kích thước khối, (
ví dụ 128 bit ), các chế độ xử lý ( mode of operation )
được sử dụng.
– Mã hóa khối tương phản với mã hóa dòng ( stream 
cipher ), trong đó mỗi ký tự được thao tác một lần và
quá trình chuyển đổi thay đổi trong suốt quá trình mã
hóa.
– Ví dụ mã hóa khối:
z Thuật toán DES do công ty IBM xây dựng và công bố năm 
1977.
z Hậu duệ của DES, Advanced Encryption Standard (AES), ra 
đời năm 2001.
Mã hóa khối ( block cipher )
z Mật mã khối gồm một cặp thuật toán:
– Thuật toán mã hóa, E, và
– Thuật toán giải mã, E-1.
– Cả hai thuật toán đều có hai đầu vào:
z Khối dữ liệu đầu vào kích thước n bit và
z Khóa độ dài k bit,
– Đầu ra là khối dữ liệu kích thước n-bit.
Mã hóa khối ( block cipher )
Mật mã dòng ( Stream Cipher )
z Mật mã dòng là mật mã khóa đối xứng, trong đó các ký tự của bản rõ
được mã hóa lần lượt và quá trình biến đổi các ký tự tiếp theo thay đổi 
trong quá trình mã hóa. Một tên khác của mật mã dòng là mật mã trạng 
thái vì quá trình mã hóa từng ký tự phụ thuộc vào trạng thái hiện thời.
Trong thựcc tiễn, ký tự có thể là từng bít hoặc byte.
z Stream ciphers represent a different approach to symmetric encryption 
from block ciphers. Block ciphers operate on large blocks of digits with 
a fixed, unvarying transformation. This distinction is not always clear-
cut: in some modes of operation, a block cipher primitive is used in 
such a way that it acts effectively as a stream cipher. Stream ciphers 
typically execute at a higher speed than block ciphers and have lower 
hardware complexity. However, stream ciphers can be susceptible to 
serious security problems if used incorrectly: see stream cipher attacks
— in particular, the same starting state must never be used twice.