Bài giảng An toàn an ninh mạng - Bài 2: Các hệ mật mã - Bùi Trọng Tùng
Khái niệm mật mã
• Mã hóa (code): biến đổi cách thức biểu diễn thông tin
• Mật mã (cipher): mã hóa để che giấu, giữ mật thông tin
Lưu trữ
Truyền tin
• Mật mã học (cryptography): ngành khoa học nghiên cứu
các phương pháp toán học để mã hóa giữ mật thông tin
• Thám mã (cryptoanalysis): nghiên cứu các phương pháp
toán học để phá vỡ hệ mật mã
• Là công cụ hiệu quả giải quyết bài toán ATBM, là cơ sở
cho nhiều cơ chế khác (xác thực, nhận dạng)
Nhưng không vạn năng
Xây dựng mô hình (mật mã khóa đối xứng)
• Alice và Bob đã chia sẻ thông tin bí
mật K gọi là khóa
• Alice cần gửi cho Bob một thông điệp
M (bản rõ). Nội dung thông điệp cần
giữ bí mật trước quan sát của Eve (kẻ
tấn công, thám mã)
Mã hóa: C = E(K, M)
C: bản mã
• Alice gửi bản mã lên kênh truyền.
Bob và Eve đều thu được thông điệp
này. Chỉ có Bob giải mã để thu được
bản rõ
Giải mã: M = D(K, C)
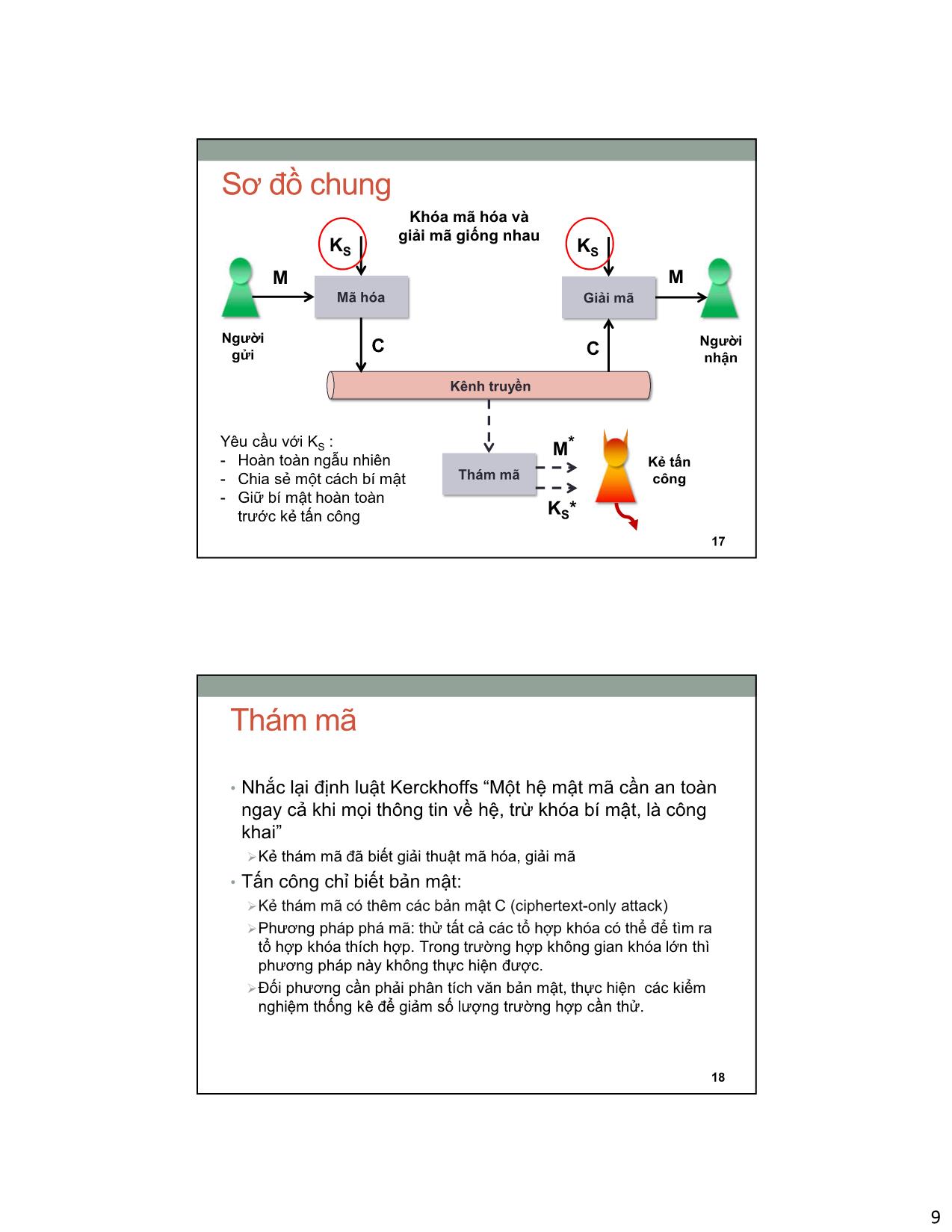
• Mật mã khóa đối xứng: dùng khóa K
trong cả hai quá trình mã hóa và giải
mã

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng An toàn an ninh mạng - Bài 2: Các hệ mật mã - Bùi Trọng Tùng

BÀI 2. CÁC HỆ MẬT Mà Bùi Trọng Tùng, Viện Công nghệ thông tin và Truyền thông, Đại học Bách khoa Hà Nội 1 Nội dung • Mật mã (cipher) là gì? • Nguyên tắc chung của các hệ mật mã • Hệ mật mã khóa đối xứng • Hệ mật mã khóa bất đối xứng 2 1 1. MẬT Mà LÀ GÌ? Bùi Trọng Tùng, Viện Công nghệ thông tin và Truyền thông, Đại học Bách khoa Hà Nội 3 1.1. Khái niệm mật mã • Mã hóa (code): biến đổi cách thức biểu diễn thông tin • Mật mã (cipher): mã hóa để che giấu, giữ mật thông tin Lưu trữ Truyền tin • Mật mã học (cryptography): ngành khoa học nghiên cứu các phương pháp toán học để mã hóa giữ mật thông tin • Thám mã (cryptoanalysis): nghiên cứu các phương pháp toán học để phá vỡ hệ mật mã • Là công cụ hiệu quả giải quyết bài toán ATBM, là cơ sở cho nhiều cơ chế khác (xác thực, nhận dạng) Nhưng không vạn năng 4 2 Truyền tin bí mật Google Mail • Bước 1: Trao đổi khóa • Bước 2: Mã hóa dữ liệu 5 Lưu trữ thông tin mật Alice Alice Thiết bị lưu trữ Alice “hôm nay” truyền tin bí mật cho Alice “ngày mai” 6 3 Xây dựng mô hình (mật mã khóa đối xứng) • Alice và Bob đã chia sẻ thông tin bí Alice Bob mật K gọi là khóa • Alice cần gửi cho Bob một thông điệp M (bản rõ). Nội dung thông điệp cần giữ bí mật trước quan sát của Eve (kẻ tấn công, thám mã) Mã hóa: C = E(K, M) C: bản mã • Alice gửi bản mã lên kênh truyền. Bob và Eve đều thu được thông điệp này. Chỉ có Bob giải mã để thu được Eve bản rõ Giải mã: M = D(K, C) • Mật mã khóa đối xứng: dùng khóa K trong cả hai quá trình mã hóa và giải mã 7 Một ví dụ - Mật mã Caesar • Julius Caesar đưa ra vào thế kỷ thứ 1 trước CN, sử dụng trong quan sự • Ý tưởng: thay thế một ký tự (bản rõ) trong bảng chữ cái bằng ký tự (bản mật) đứng sau nó 3 (khóa) vị trí. Sử dụng bảng chữ cái vòng A D, B E, C F,..., X A, Y B, Z C • Mô hình hóa bằng toán học: Khóa K = 3 Mã hóa: C = (M+3) mod 26 Giải mã: M = (C − 3) mod 26 • Dễ dàng bị phá ngay cả khi K thay đổi Gaius Julius Caesar các giá trị khác 8 4 1.2. Một số nguyên lý chung của các hệ mật mã • Định luật Kerckhoffs: “Một hệ mật mã cần an toàn ngay cả khi mọi thông tin về hệ, trừ khóa bí mật, là công khai” • Tại sao? 9 Lý thuyết Shannon • Hệ mật hoàn hảo: độ an toàn của hệ mật không phụ thuộc vào số bản mã và thời gian kẻ tấn công sử dụng để thám mã (An toàn vô điều kiện) • Lý thuyết Shannon: Một hệ mật mã là hoàn hảo thì Độ dài của khóa tối thiểu bằng độ dài bản tin rõ Khóa chỉ sử dụng một lần Điều kiện cần Tại sao khó đạt được trên thực tế? • An toàn theo tính toán: thỏa mãn đồng thời 2 điều kiện Thời gian để thám mã thành công lớn hơn thời gian cần giữ mật thông tin Chi phí để thám mã thành công lớn hơn giá trị thông tin thu được 10 5 Lý thuyết Shannon (tiếp) • Độ dư thừa của ngôn ngữ: Sự xuất hiện của n ký tự (n- gram) cho phép đoán nhận đúng các ký tự xuất hiện tiếp theo với xác xuất p nào đó. Nếu p = 0 ∀n: ngôn ngữ không có dư thừa Nếu p > 0: ngôn ngữ có dư thừa (một số ký tự là không cần thiết sau khi n ký tự đã xuất hiện) Định lượng: sử dụng lý thuyết thông tin Ví dụ: tiếng Việt • Đối với thám mã: sử dụng phương pháp vét cạn, cần phải thu được tối thiểu u ký tự mật mã để tìm được chính xác khóa. u: khoảng cách unicity (unicity distance) u càng lớn độ an toàn của hệ càng cao 11 Lý thuyết Shannon (tiếp) • Tính toán khoảng cách unicity � �(�) � = � � � − �(�) ��: Kích thước khóa � � , � � , � � : entropy của ký tự. Ví dụ � � = − ∑ � �� × ���2(�(��)): entropy của ký tự bản rõ � �� : xác suất xuất hiện của ký tự trong không gian bản rõ • Nếu khóa và bản mật xuất hiện hoàn toàn ngẫu nhiên, và chung bảng chữ cái: � ��� (�) � = � 2 ���2(�) − �(�) N: số ký tự của bảng chữ cái • Làm thế nào để tăng độ an toàn khi sử dụng mật mã? 12 6 Thông tin tham khảo – Kích thước khóa • Khóa có kích thước bao nhiêu? Mật mã được coi là an toàn khi phương pháp vét cạn (brute-force) là cách nhanh nhất để bẻ khóa Mục tiêu: giảm thiểu nguy cơ bị tấn công vét cạn (đạt độ an toàn theo tính toán) • Bạn nghe ở đâu đó, “dễ dàng” bẻ khóa mật mã DES có kích thước khóa 64 bit? Năm 1999, hệ thống phá mã EFF DES (trị giá 250K$) bẻ khóa DES trong khoảng 1 ngày Năm 2008, hệ thống phá mã COPACOBANA (trị giá 10K$) bẻ khóa DES trong 6,4 ngày Sử dụng định luật Moore để tính thời gian bẻ khóa trong năm 2016 với chi phí 10K$? 13 Thông tin tham khảo – Kích thước khóa • Chi phí để bẻ khóa DES (năm 2008) 64 bit: $10.000 87 bit: $10.000.000.000 (thời gian bẻ khóa không đổi) • Cần giữ thông tin mật trong bao lâu khi hệ thống phá mã là COPACOBANA? (năm 2008) 64 bit: 6.4 ngày 128 bit: ? • Tuy nhiên, vét cạn là phương pháp tấn công tầm thường. • Tham khảo kích thước khóa nên sử dụng trong tương lai tại địa chỉ 14 7 2. Hệ mật mã khóa đối xứng • Symmetric cryptography, Secret-key cryptography: sử dụng cùng một khóa khi mã hóa và giải mã. • Được phát triển từ rất sớm • Thuật toán mã hóa: phối hợp các toán tử Thay thế Đổi chỗ XOR (Tại sao dùng XOR?) • Tốc độ thực hiện các thuật toán nhanh, có thể thực hiện bằng dễ dàng bằng phần cứng • Một số hệ mật mã khóa đối xứng hiện đại: DES, 2DES, 3DES, AES, RC4, RC5 Việc tìm hiểu đặc điểm những hệ mật mã này coi như một bài tập!!! 15 2.1. Sơ đồ chung • Hệ mật mã gồm: Bản rõ (plaintext-M): bản tin được sinh ra bởi bên gửi Bản mật (ciphertext-C): bản tin che giấu thông tin của bản rõ, được gửi tới bên nhận qua một kênh không bí mật Khóa (key-KS): giá trị ngẫu nhiên và bí mật được chia sẻ giữa các bên trao đổi thông tin Bên thứ 3 được tin cậy tạo và phân phối tới bên gửi và bên nhận Hoặc, bên nguồn tạo và chuyển cho bên nhận Mã hóa (encrypt-E): C = E(KS, M) Giải mã (decrypt): M = D(KS, C) = D(KS, E(KS, M)) 16 8 Sơ đồ chung Khóa mã hóa và giải mã giống nhau KS KS M M Mã hóa Giải mã Người C Người gửi C nhận Kênh truyền Yêu cầu với KS : M* - Hoàn toàn ngẫu nhiên Kẻ tấn - Chia sẻ một cách bí mật Thám mã công - Giữ bí mật hoàn toàn trước kẻ tấn công KS* 17 Thám mã • Nhắc lại định luật Kerckhoffs “Một hệ mật mã cần an toàn ngay cả khi mọi thông tin về hệ, trừ khóa bí mật, là công khai” Kẻ thám mã đã biết giải thuật mã hóa, giải mã • Tấn công chỉ biết bản mật: Kẻ thám mã có thêm các bản mật C (ciphertext-only attack) Phương pháp phá mã: thử tất cả các tổ hợp khóa có thể để tìm ra tổ hợp khóa thích hợp. Trong trường hợp không gian khóa lớn thì phương pháp này không thực hiện được. Đối phương cần phải phân tích văn bản mật, thực hiện các kiểm nghiệm thống kê để giảm số lượng trường hợp cần thử. 18 9 Thám mã (tiếp) • Tấn công đã biết bản rõ (known-plaintext attack): Kẻ thám mã đã có một số cặp (M,C) của những phiên truyền tin trước đó. Mục đích: đoán khóa mật K. Phương pháp tấn công: phân tích thuộc tính thống kê của ngôn ngữ trên văn bản gốc • Tấn công chọn trước bản rõ (chosen-plaintext attack): kẻ thám mã lừa người gửi mã hóa một số bản tin đặc biệt do hắn chọn • Tấn công chọn trước bản mật(chosen-ciphertext attack): kẻ thám mã lừa người nhận giải mã một số bản tin đặc biệt do hắn chọn • Tấn công chọn trước bản rõ, bản mật Thuật toán được thiết kế để chống lại dạng tấn công này 19 Mật mã one-time-pad •Vernam (1917) Key: 0 1 0 1 1 1 0 0 1 0 Plaintext: 1 1 0 0 0 1 1 0 0 0 Ciphertext: 1 0 0 1 1 0 1 0 1 0 • Kích thước của khóa bằng kích thước của bản rõ • Khóa chỉ dùng 1 lần • Shannon : mật mã one-time-pad là hệ mật hoàn hảo 20 10 2.2. Mật mã dòng (stream cipher) • Xử lý văn bản rõ theo dòng byte, thời gian thực RC4 (900 Mbps), SEAL (2400 Mbps), RC5(450 Mbps) • Phù hợp với các hệ thống truyền dữ liệu thời gian thực trên môi trường mạng máy tính • An toàn nếu khóa hoàn toàn ngẫu nhiên, chỉ dùng 1 lần (one-time-pad) Trên thực tế: khóa giả ngẫu nhiên dùng nhiều lần (n-time-pad) một số phương pháp mật mã dòng không còn an toàn (RC4) 21 2.3. Mật mã khối • Chia văn bản gốc thành các khối có kích thước như nhau • Xử lý mã hóa và giải mã từng khối độc lập • ECB - Electronic Code Book (Chế độ mã từ điển) Bản rõ: m1 m2 Bản mã: c1 c2 • Hạn chế? 22 11 Ví dụ về mật mã khối chế độ ECB Ảnh gốc Ảnh được mã hóa ở chế độ ECB 23 Chế độ CBC - Cipher Block Chaining • Chế độ mã móc xích • Có thể thay thế mã dòng: Ưu điểm? Hạn chế? IV m[0] m[1] m[2] m[3] KS Mã KS Mã KS Mã KS Mã hóa hóa hóa hóa IV c[0] c[1] c[2] c[3] 24 12 CBC – Giải mã IV c[0] c[1] c[2] c[3] KS Giải KS Giải Giải Giải KS KS mã mã mã mã IV m[0] m[1] m[2] m[3] 25 CBC – So sánh với ECB Ảnh gốc Mã hóa ở chế độ Mã hóa ở chế độ ECB CBC 26 13 2.4. Những hạn chế của mật mã khóa đối xứng • Cần kênh mật để chia sẻ khóa bí mật giữa các bên Làm sao để chia sẻ một cách an toàn cho lần đầu tiên • Số lượng khóa lớn: n(n-1)/2 • Khó ứng dụng trong các hệ thống mở (E-commerce) • Không dễ dàng để xác thực đối với thông tin quảng bá (Chúng ta sẽ quay trở lại vấn đề này trong những bài sau) 27 3. Hệ mật mã khóa bất đối xứng • Asymmetric key cryptography, Public key cryptography • Tháng 11/1976, Diffie và Hellman giới thiệu ý tưởng về một kịch bản chia sẻ khóa bí mật (của hệ mật mã khóa đối xứng) mới mà không truyền trực tiếp giá trị của khóa. • Độ an toàn dựa trên độ khó khi giải một số bài toán: Phân tích một số thành thừa số nguyên tố Tính logarit rời rạc • Các thuật toán dựa trên các hàm toán học • Một số hệ mật mã khóa công khai: RSA, El-Gamal 28 14 3.1. Kịch bản trao đổi khóa bí mật của Diffie-Hellman • Alice và Bob cùng chia sẻ một khóa nhóm (q, a). Trong đó q là một số nguyên tố 1< a < q thỏa mãn: (ai mod q) ≠ aj mod q ∀ 1 < i ≠ j < q A B XA < q XB < q X X YA = a A mod q YB = a B mod q YA YB X X K = Y B mod q KS = YB A mod q S A 29 Ví dụ • Khóa chung của nhóm q = 71, a = 7 Hãy tự kiểm tra điều kiện thỏa mãn của a 5 • A chọn XA = 5, tính YA = 7 mod 71 = 51 A B X = 5 A XB = 12 5 YA = 7 mod 71 = 51 Y = 712 mod 71 = 4 YA B 12 KS = 51 mod 71 = 30 YB 5 KS = 4 mod 71 = 30 • Vấn đề an toàn của sơ đồ này sẽ được xem xét đến sau. Rút ra được điều gì từ sơ đồ này? 30 15 3.2. Sơ đồ chung • Hệ mật mã gồm: Bản rõ (plaintext-M): bản tin được sinh ra bởi bên gửi Bản mật (ciphertext-C): bản tin che giấu thông tin của bản rõ, được gửi tới bên nhận qua một kênh không bí mật Khóa: Bên nhận có 1 cặp khóa: Khóa công khai KUB : công bố cho tất cả biết (trong đó có cả kẻ tấn công) Khóa cá nhân KRB : bên nhận giữ bí mật, không chia sẻ Mã hóa (encrypt-E): C = E(KUB, M) Giải mã (decrypt): M = D(KRB, C) = D(KRB, E(KUB, M)) 31 3.2. Sơ đồ chung (tiếp) Khóa mã hóa và giải mã khác nhau KUB KRB M M Mã hóa Giải mã Người Người Gửi (A) C C nhận (B) Kênh truyền Làm thế nào để B M* Kẻ tấn gửi tin một cách bí Thám mã mật cho A? công K* RB 32 16 3.2. Sơ đồ chung (tiếp) • Yêu cầu đối với cặp khóa (KUB, KRB) Hoàn toàn ngẫu nhiên Có quan hệ về mặt toán học 1-1, nhưng... Nếu chỉ có giá trị của KUB không thể tính được KRB KRB phải được giữ mật hoàn toàn 33 Một ví dụ - Hệ mật RSA • Sinh khóa: Chọn p,q là hai số nguyên tố Tính n = p q , (n) = (p-1) (q-1) Chọn e sao cho UCLN((n), e) = 1 ;1< e < (n) Tính d sao cho (e d) mod (n) =1. Khóa công khai : KU = (e,n) Khóa riêng : KR = (d,n) • Mã hóa : C = Me mod n • Giải mã: M = Cd mod n 34 17 Một ví dụ - Hệ mật RSA • Sinh khóa: Chọn p = 5, q = 11 Tính n = p × q = 55, (n) =(p-1)×(q-1) = 40 Chọn e sao cho UCLN((n), e) = 1 và 1 < e < (n) VD: e = 7 Tính d sao cho (e × d) mod (n) = 1, 1 < d < (n) d = 23 Cặp khóa : KU = (7,55), KR = (23,55) • Mã hóa: M = 6 C = 41 • Giải mã: C = 41 M = 6 Nếu kẻ tấn công có KU, làm thế nào để tính KR? 35 3.3. Kết hợp mật mã khóa công khai và mật mã khóa đối xứng • Ưu điểm của mật mã khóa công khai: Không cần chia sẻ khóa mã hóa KUB một cách bí mật Dễ dàng ứng dụng trong các hệ thống mở Khóa giải mã KRB chỉ có B biết: An toàn hơn Có thể sử dụng KRB để xác thực nguồn gốc thông tin (Chúng ta sẽ quay lại vấn đề này trong bài sau) Số lượng khóa để mã mật tỉ lệ tuyến tính với số phần tử (n phần tử n cặp khóa) • Nhưng... 36 18 3.3. Kết hợp mật mã khóa công khai và mật mã khóa đối xứng • Vấn đề cần giải quyết trong hệ mật mã khóa công khai Vẫn cần kênh an toàn để chia sẻ khóa. VD: Tấn công vào sơ đồ Diffie-Hellman bằng kỹ thuật man-in-the- middle 37 3.3. Kết hợp mật mã khóa công khai và mật mã khóa đối xứng • Hạn chế của mật mã khóa công khai so với mật mã khóa đối xứng: Kém hiệu quả hơn: khóa có kích thước lớn hơn, chi phí tính toán cao hơn Có thể bị tấn công toán học Kết hợp 2 hệ mật mã 38 19 Sơ đồ “lai” • Phía gửi Thông điệp (bản rõ) KUB Mã hóa Thông điệp Bản mã KĐX được mã hóa Mã hóa Khóa được KS KCK mã hóa Nguồn khóa bí mật Tự suy luận cách thức xử lý của phía nhận như là một bài tập! 39 Kết luận • Những sai lầm khi sử dụng mật mã: Mật mã là giải pháp vạn năng (những bài sau chúng ta sẽ phân tích kỹ hơn) Khóa có kích thước lớn, mã hóa sẽ an toàn Sửa đổi/Thêm một vài yếu tố bí mật vào giải thuật, hệ mật mã sẽ an toàn hơn 40 20 Kết luận • Chỉ sử dụng thuật toán chuẩn • Đừng tự thiết kế hệ mật mã cho riêng mình: Nếu không thể sử dụng các hệ mật mã đã có, hãy xem lại hệ thống Nếu bắt buộc phải sử dụng hệ mật mã mới hoàn toàn, hãy đánh giá một cách cẩn thận • Sử dụng khóa khác nhau cho các mục đích khác nhau • Mật mã chưa đáp ứng yêu cầu về toàn vẹn Khi sử dụng mật mã hãy thêm vào các sơ đồ đáp ứng toàn vẹn nội dung thông tin và xác thực nguồn gốc thông tin (sẽ đề cập đến trong những bài sau) • Sinh khóa: Sử dụng những hàm sinh số ngẫu nhiên cho mật mã Đừng sử dụng những hàm sinh số ngẫu nhiên chuẩn rand(), srand()... 41 21
File đính kèm:
 bai_giang_an_toan_an_ninh_mang_bai_2_cac_he_mat_ma_bui_trong.pdf
bai_giang_an_toan_an_ninh_mang_bai_2_cac_he_mat_ma_bui_trong.pdf

