Bài giảng An ninh mạng - Chương 3, Phần 2: Mật mã khóa công khai - Nguyễn Đại Thọ

 Chương 3
 MẬT MÃ KHÓA CÔNG KHAI
Nguyễn Đại Thọ An ninh Mạng 83
 Giới thiệu
• Những hạn chế của mật mã đối xứng
 – Vấn đề phân phối khóa
 • Khó đảm bảo chia sẻ mà không làm lộ khóa bí mật
 • Trung tâm phân phối khóa có thể bị tấn công
 – Không thích hợp cho chữ ký số
 • Bên nhận có thể làm giả thông báo nói nhận được từ bên gửi
• Mật mã khóa công khai đề xuất bởi Whitfield 
 Diffie và Martin Hellman vào năm 1976
 – Khắc phục những hạn chế của mật mã đối xứng
 – Có thể coi là bước đột phá quan trọng nhất trong lịch 
 sử của ngành mật mã
 – Bổ xung chứ không thay thế mật mã đối xứng
Nguyễn Đại Thọ An ninh Mạng 84
Đặc điểm mật mã khóa công khai
 • Còn gọi là mật mã hai khóa hay bất đối xứng
 • Các giải thuật khóa công khai sử dụng 2 khóa
 – Một khóa công khai
 • Ai cũng có thể biết
 • Dùng để mã hóa thông báo và thẩm tra chữ ký
 – Một khóa riêng
 • Chỉ nơi giữ được biết
 • Dùng để giải mã thông báo và ký (tạo ra) chữ ký
 • Có tính bất đối xứng
 – Bên mã hóa không thể giải mã thông báo
 – Bên thẩm tra không thể tạo chữ ký
 Nguyễn Đại Thọ An ninh Mạng 85
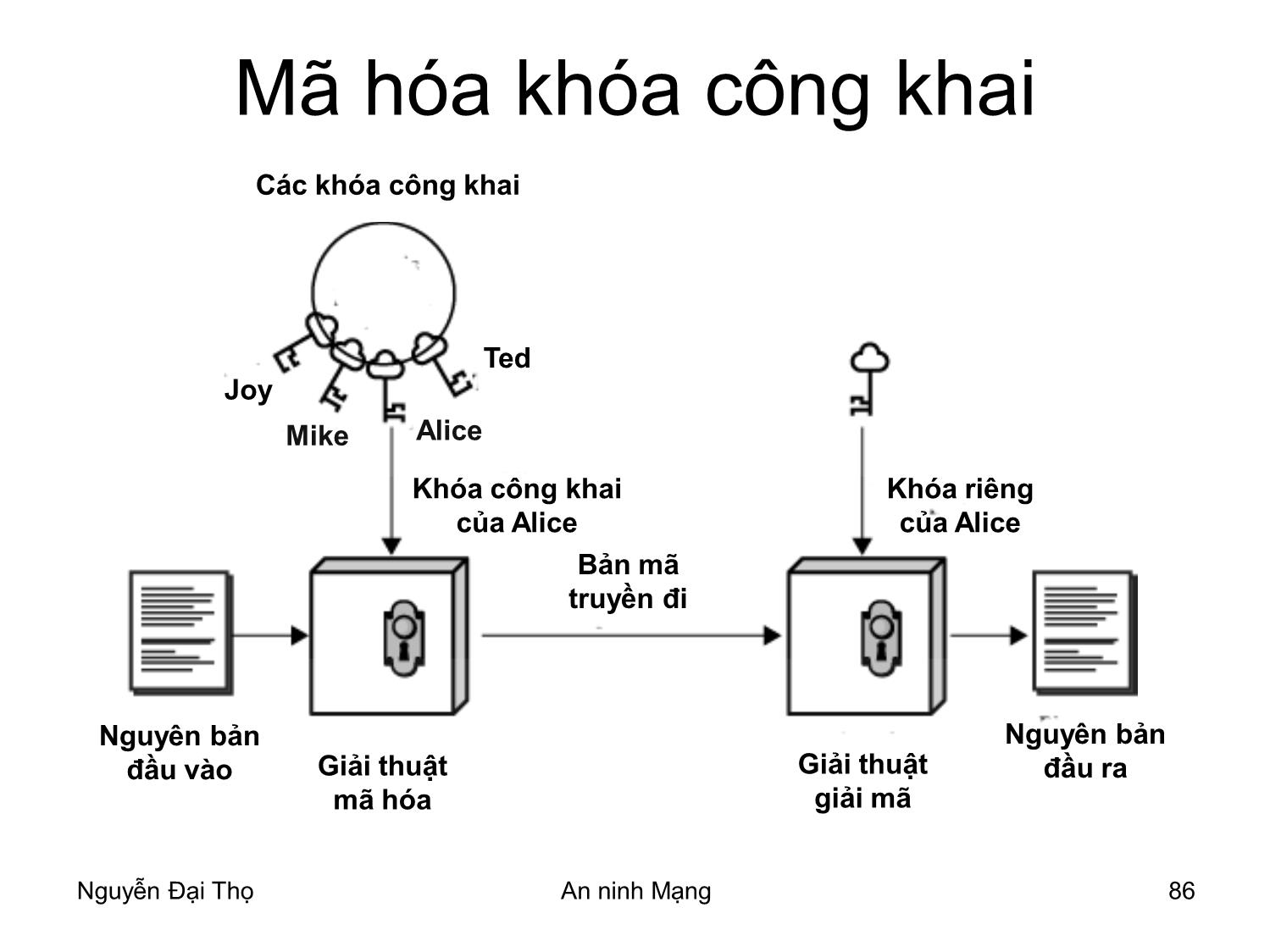
 Mã hóa khóa công khai
 Các khóa công khai
 Ted
 Joy
 Mike Alice
 Khóa công khai Khóa riêng
 của Alice của Alice
 Bản mã
 truyền đi
 Nguyên bản Nguyên bản
 đầu vào Giải thuật Giải thuật đầu ra
 mã hóa giải mã
Nguyễn Đại Thọ An ninh Mạng 86
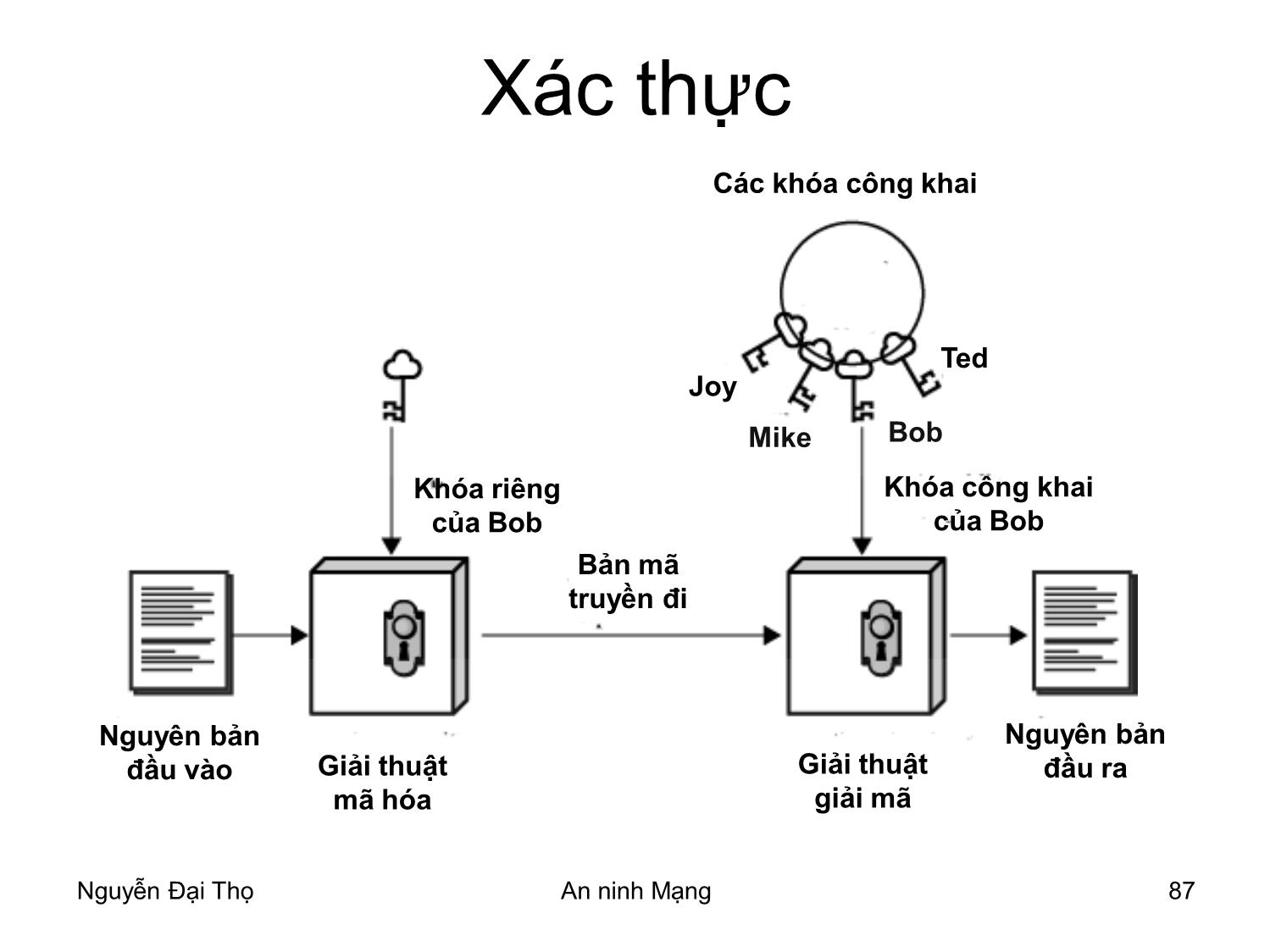
 Xác thực
 Các khóa công khai
 Ted
 Joy
 Mike Bob
 Khóa riêng Khóa công khai
 của Bob của Bob
 Bản mã
 truyền đi
 Nguyên bản Nguyên bản
 đầu vào Giải thuật Giải thuật đầu ra
 mã hóa giải mã
Nguyễn Đại Thọ An ninh Mạng 87
Ứng dụng mật mã khóa công khai
 • Có thể phân ra 3 loại ứng dụng
 – Mã hóa/giải mã
 • Đảm bảo sự bí mật của thông tin
 – Chữ ký số
 • Hỗ trợ xác thực văn bản
 – Trao đổi khóa
 • Cho phép chia sẻ khóa phiên trong mã hóa đối xứng
 • Một số giải thuật khóa công khai thích hợp cho 
 cả 3 loại ứng dụng; một số khác chỉ có thể dùng 
 cho 1 hay 2 loại
 Nguyễn Đại Thọ An ninh Mạng 88
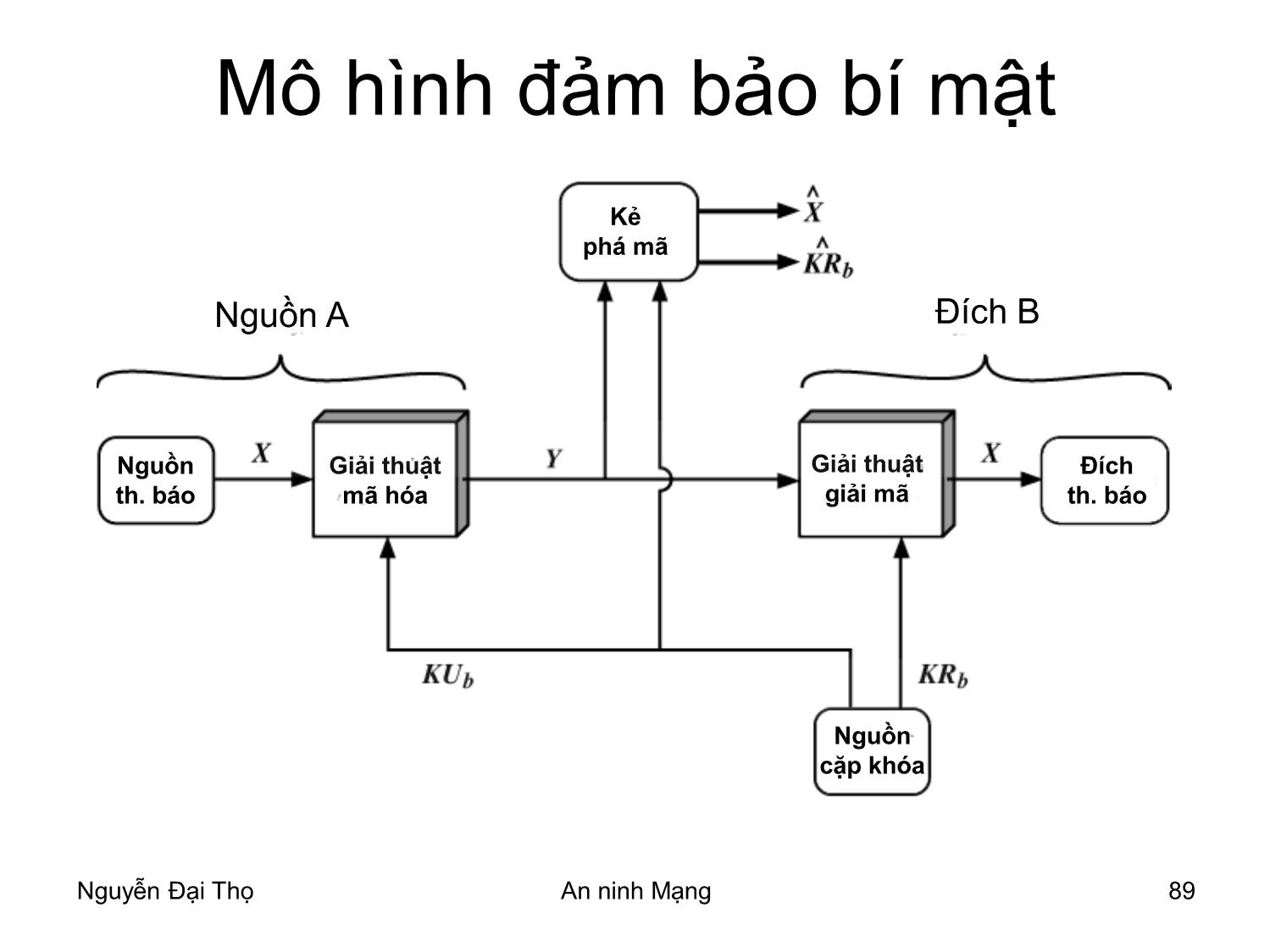
 Mô hình đảm bảo bí mật
 Kẻ
 phá mã
 Nguồn A Đích B
 Nguồn Giải thuật Giải thuật Đích
 th. báo mã hóa giải mã th. báo
 Nguồn
 cặp khóa
Nguyễn Đại Thọ An ninh Mạng 89
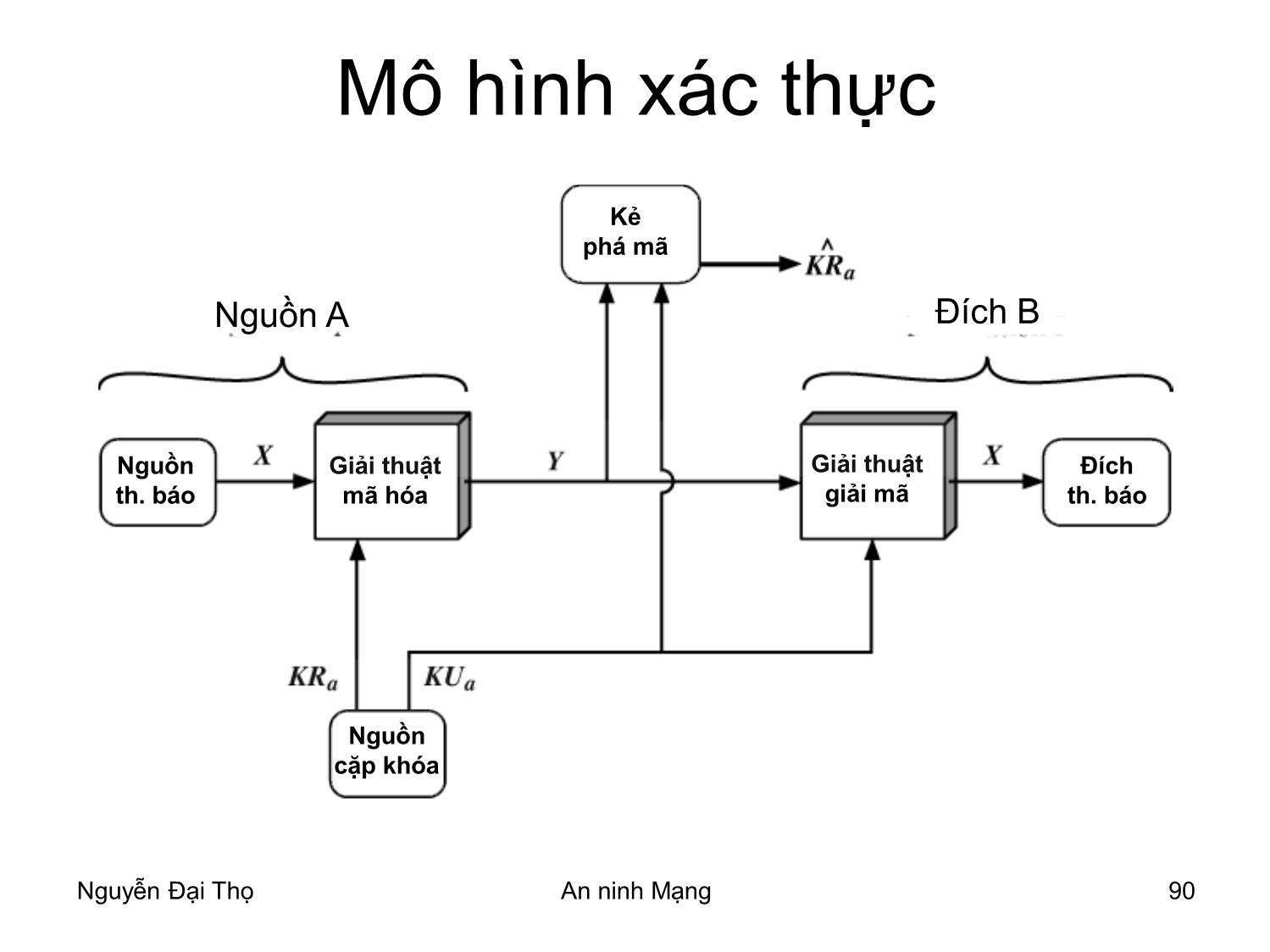
 Mô hình xác thực
 Kẻ
 phá mã
 Nguồn A Đích B
 Nguồn Giải thuật Giải thuật Đích
 th. báo mã hóa giải mã th. báo
 Nguồn
 cặp khóa
Nguyễn Đại Thọ An ninh Mạng 90
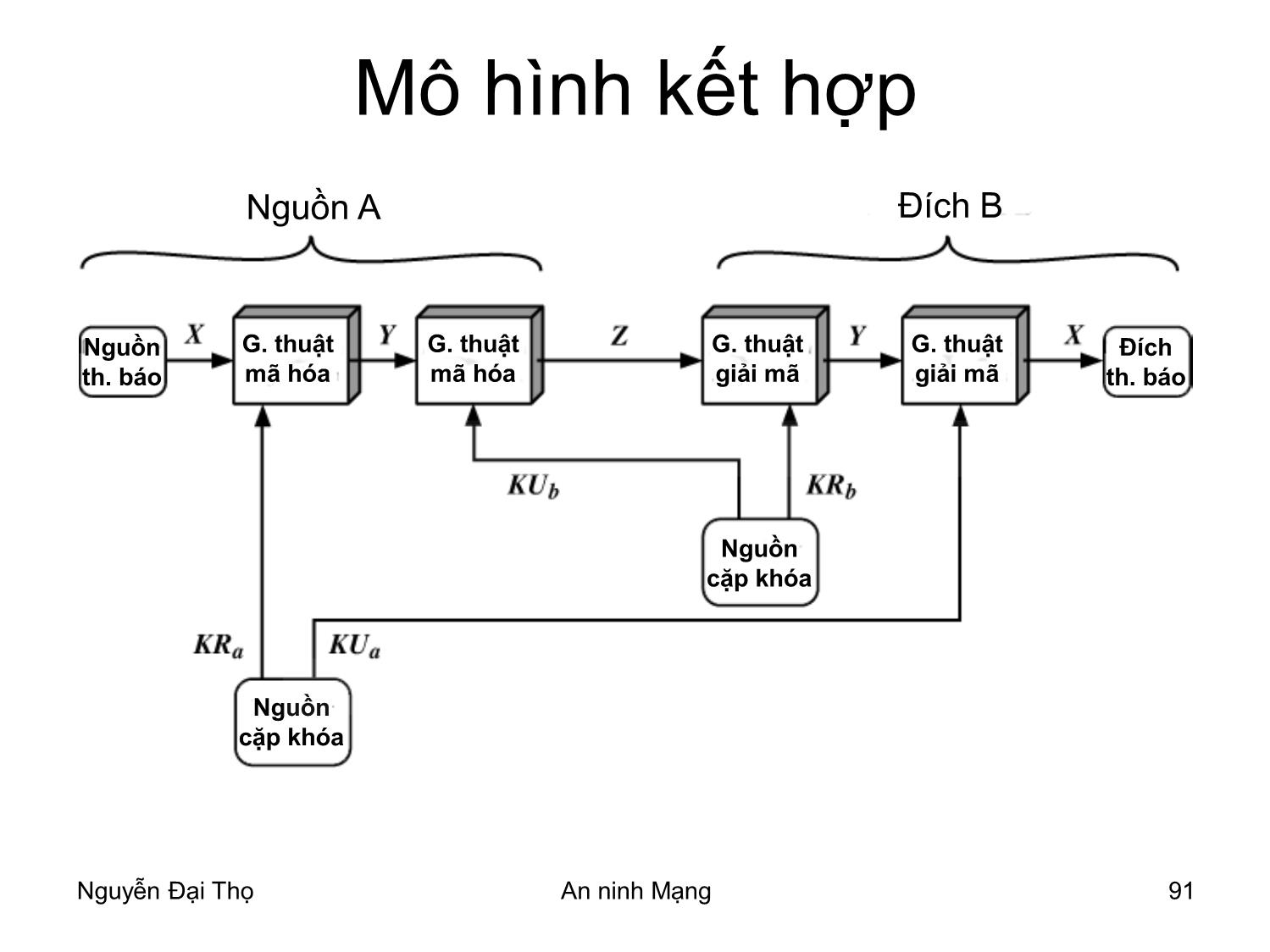
 Mô hình kết hợp
 Nguồn A Đích B
Nguồn G. thuật G. thuật G. thuật G. thuật Đích
th. báo mã hóa mã hóa giải mã giải mã th. báo
 Nguồn
 cặp khóa
 Nguồn
 cặp khóa
Nguyễn Đại Thọ An ninh Mạng 91
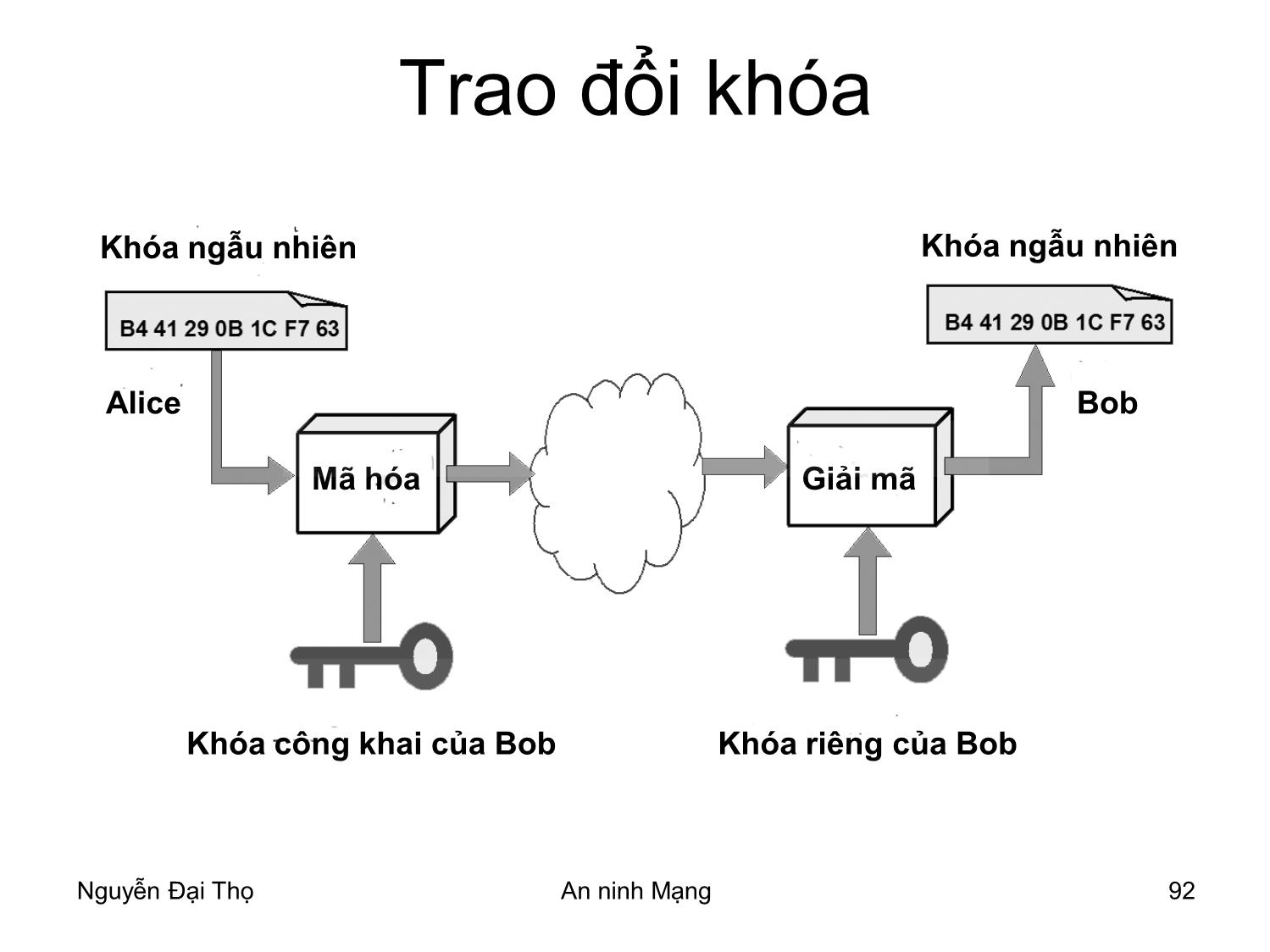
 Trao đổi khóa
 Khóa ngẫu nhiên Khóa ngẫu nhiên
 Alice Bob
 Mã hóa Giải mã
 Khóa công khai của Bob Khóa riêng của Bob
Nguyễn Đại Thọ An ninh Mạng 92
 Các điều kiện cần thiết
• Bên B dễ dàng tạo ra được cặp (KUb, KRb)
• Bên A dễ dàng tạo ra được C = E (M)
 KUb
• Bên B dễ dàng giải mã M = D (C)
 KRb
• Đối thủ không thể xác định được KRb khi biết KUb
• Đối thủ không thể xác định được M khi biết KUb
 và C
• Một trong hai khóa có thể dùng mã hóa trong khi 
 khóa kia có thể dùng giải mã
 – M = D (E (M)) = D (E (M))
 KRb KUb KUb KRb
 – Không thực sự cần thiết
Nguyễn Đại Thọ An ninh Mạng 93
 Hệ mã hóa RSA
• Đề xuất bởi Ron Rivest, Adi Shamir và Len 
 Adleman (MIT) vào năm 1977
• Hệ mã hóa khóa công khai phổ dụng nhất
• Mã hóa khối với mỗi khối là một số nguyên < n
 – Thường kích cỡ n là 1024 bit ≈ 309 chữ số thập phân
• Đăng ký bản quyền năm 1983, hết hạn năm 2000
• An ninh vì chi phí phân tích thừa số của một số 
 nguyên lớn là rất lớn
Nguyễn Đại Thọ An ninh Mạng 94
 Tạo khóa RSA
• Mỗi bên tự tạo ra một cặp khóa công khai - khóa 
 riêng theo các bước sau :
 – Chọn ngẫu nhiên 2 số nguyên tố đủ lớn p q
 – Tính n = pq
 – Tính (n) = (p-1)(q-1)
 – Chọn ngẫu nhiên khóa mã hóa e sao cho 1 < e < (n) 
 và gcd(e, (n)) = 1
 – Tìm khóa giải mã d ≤ n thỏa mãn e.d ≡ 1 mod (n)
• Công bố khóa mã hóa công khai KU = {e, n}
• Giữ bí mật khóa giải mã riêng KR = {d, n}
 – Các giá trị bí mật p và q bị hủy bỏ
Nguyễn Đại Thọ An ninh Mạng 95
 Thực hiện RSA
• Để mã hóa 1 thông báo nguyên bản M, bên gửi 
 thực hiện
 – Lấy khóa công khai của bên nhận KU = {e, n}
 – Tính C = Me mod n
• Để giải mã bản mã C nhận được, bên nhận thực 
 hiện
 – Sử dụng khóa riêng KR = {d, n}
 – Tính M = Cd mod n
• Lưu ý là thông báo M phải nhỏ hơn n
 – Phân thành nhiều khối nếu cần
Nguyễn Đại Thọ An ninh Mạng 96
 Vì sao RSA khả thi
• Theo định lý Euler
 – a, n : gcd(a, n) = 1 a (n) mod n = 1
 – (n) là số các số nguyên dương nhỏ hơn n và nguyên 
 tố cùng nhau với n
• Đối với RSA có
 – n = pq với p và q là các số nguyên tố
 – (n) = (p - 1)(q - 1)
 – ed ≡ 1 mod (n) số nguyên k : ed = k (n) + 1
 – M < n
• Có thể suy ra
 – Cd mod n = Med mod n = Mk (n) + 1 mod n = M mod n = M
Nguyễn Đại Thọ An ninh Mạng 97
 Ví dụ tạo khóa RSA
• Chọn 2 số nguyên tố p = 17 và q = 11
• Tính n = pq = 17 11 = 187
• Tính (n) = (p - 1)(q - 1) = 16 10 = 160
• Chọn e : gcd(e, 160) = 1 và 1 < e < 160; lấy e = 7
• Xác định d : de ≡ 1 mod 160 và d ≤ 187
 Giá trị d = 23 vì 23 7 = 161 = 1 160 + 1
• Công bố khóa công khai KU = {7, 187}
• Giữ bí mật khóa riêng KR = {23, 187}
 – Hủy bỏ các giá trị bí mật p = 17 và q = 11
Nguyễn Đại Thọ An ninh Mạng 98
 Ví dụ thực hiện RSA
 Mã hóa Giải mã
 Bản
Nguyên mã Nguyên
 bản bản
 Nguyễn Đại Thọ An ninh Mạng 99
 Chọn tham số RSA
• Cần chọn p và q đủ lớn
• Thường chọn e nhỏ
• Thường có thể chọn cùng giá trị của e cho tất cả 
 người dùng
• Trước đây khuyến nghị giá trị của e là 3, nhưng 
 hiện nay được coi là quá nhỏ
• Thường chọn e = 216 - 1 = 65535
• Giá trị của d sẽ lớn và khó đoán
Nguyễn Đại Thọ An ninh Mạng 100
 An ninh của RSA
• Khóa 128 bit là một số giữa 1 và một số rất lớn
 340.282.366.920.938.000.000.000.000.000.000.000.000
• Có bao nhiêu số nguyên tố giữa 1 và số này
 ≈ n / ln(n) = 2128 / ln(2128) ≈ 
 3.835.341.275.459.350.000.000.000.000.000.000.000
• Cần bao nhiêu thời gian nếu mỗi giây có thể tính 
 được 1012 số
 Hơn 121,617,874,031,562,000 năm (khoảng 10 triệu lần 
 tuổi của vũ trụ)
• An ninh nhưng cần đề phòng những điểm yếu
Nguyễn Đại Thọ An ninh Mạng 101
 Phá mã RSA
• Phương pháp vét cạn
 – Thử tất cả các khóa riêng có thể
 • Phụ thuộc vào độ dài khóa
• Phương pháp phân tích toán học
 – Phân n thành tích 2 số nguyên tố p và q
 – Xác định trực tiếp (n) không thông qua p và q
 – Xác định trực tiếp d không thông qua (n)
• Phương pháp phân tích thời gian
 – Dựa trên việc đo thời gian giải mã
 – Có thể ngăn ngừa bằng cách làm nhiễu
Nguyễn Đại Thọ An ninh Mạng 102
 Phân tích thừa số RSA
• An ninh của RSA dựa trên độ phức tạp của việc 
 phân tích thừa số n
• Thời gian cần thiết để phân tích thừa số một số 
 lớn tăng theo hàm mũ với số bit của số đó
 – Mất nhiều năm khi số chữ số thập phân của n vượt 
 quá 100 (giả sử làm 1 phép tính nhị phân mất 1 s)
• Kích thước khóa lớn đảm bảo an ninh cho RSA
 – Từ 1024 bit trở lên
 – Gần đây nhất năm 1999 đã phá mã được 512 bit 
 (155 chữ số thập phân) 
Nguyễn Đại Thọ An ninh Mạng 103
 Hệ trao đổi khóa Diffie-Hellman
• Giải thuật mật mã khóa công khai đầu tiên
• Đề xuất bởi Whitfield Diffie và Martin Hellman 
 vào năm 1976
 – Malcolm Williamson (GCHQ - Anh) phát hiện trước 
 mấy năm nhưng đến năm 1997 mới công bố
• Chỉ dùng để trao đổi khóa bí mật một cách an 
 ninh trên các kêch thông tin không an ninh
• Khóa bí mật được tính toán bởi cả hai bên
• An ninh phụ thuộc vào độ phức tạp của việc tính 
 log rời rạc
Nguyễn Đại Thọ An ninh Mạng 104
 Thiết lập Diffie-Hellman
• Các bên thống nhất với nhau các tham số chung
 – q là một số nguyên tố đủ lớn
 – là một nguyên căn của q
 • mod q, 2 mod q,..., q-1 mod q là các số nguyên giao hoán 
 của các số từ 1 đến q - 1
• Bên A
 – Chọn ngẫu nhiên làm khóa riêng XA < q 
 XA
 – Tính khóa công khai YA = mod q
• Bên B
 – Chọn ngẫu nhiên làm khóa riêng XB < q 
 XB
 – Tính khóa công khai YB = mod q
Nguyễn Đại Thọ An ninh Mạng 105
 Trao đổi khóa Diffie-Hellman
• Tính toán khóa bí mật
 – Bên A biết khóa riêng XA và khóa công khai YB
 XA
 K = YB mod q
 – Bên B biết khóa riêng XB và khóa công khai YA
 XB
 K = YA mod q
• Chứng minh
 XB XA XB
 YA mod q = ( mod q) mod q
 = XAXB mod q
 = XBXA mod q
 = ( XB mod q)XA mod q
 XA
 = YB mod q
Nguyễn Đại Thọ An ninh Mạng 106
 Ví dụ Diffie-Hellman
• Alice và Bob muốn trao đổi khóa bí mật
• Cùng chọn q = 353 và = 3
• Chọn ngẫu nhiên các khóa riêng
 – Alice chọn XA = 97, Bob chọn XB = 233
• Tính toán các khóa công khai
 97
 – YA = 3 mod 353 = 40 (Alice)
 233
 – YB = 3 mod 353 = 248 (Bob)
• Tính toán khóa bí mật chung
 XA 97
 – K = YB mod 353 = 248 mod 353 = 160 (Alice)
 XB 233
 – K = YA mod 353 = 40 mod 353 = 160 (Bob)
Nguyễn Đại Thọ An ninh Mạng 107
 Hạn chế của khóa công khai
• Tốc độ xử lý
 – Các giải thuật khóa công khai chủ yếu dùng các phép 
 nhân chậm hơn nhiều so với các giải thuật đối xứng
 – Không thích hợp cho mã hóa thông thường
 – Thường dùng trao đổi khóa bí mật đầu phiên truyền tin
• Tính xác thực của khóa công khai
 – Bất cứ ai cũng có thể tạo ra một khóa công bố đó là 
 của một người khác
 – Chừng nào việc giả mạo chưa bị phát hiện có thể đọc 
 được nội dung các thông báo gửi cho người kia
 – Cần đảm bảo những người đăng ký khóa là đáng tin
Nguyễn Đại Thọ An ninh Mạng 108