Ảnh hưởng của tỉ lệ đột biến tới kết quả ước lượng trạng thái hệ thống điện bằng thuật toán di truyền

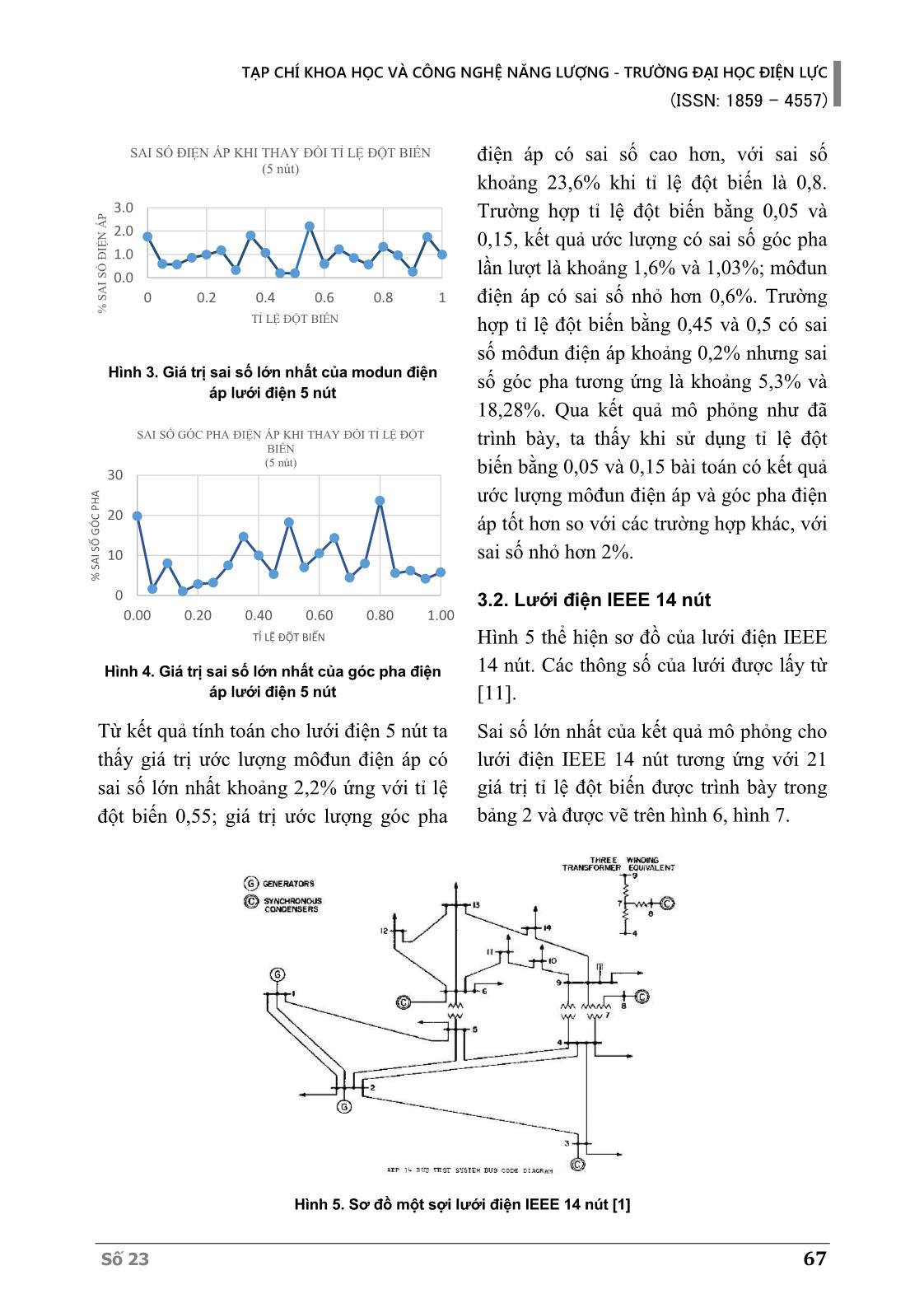
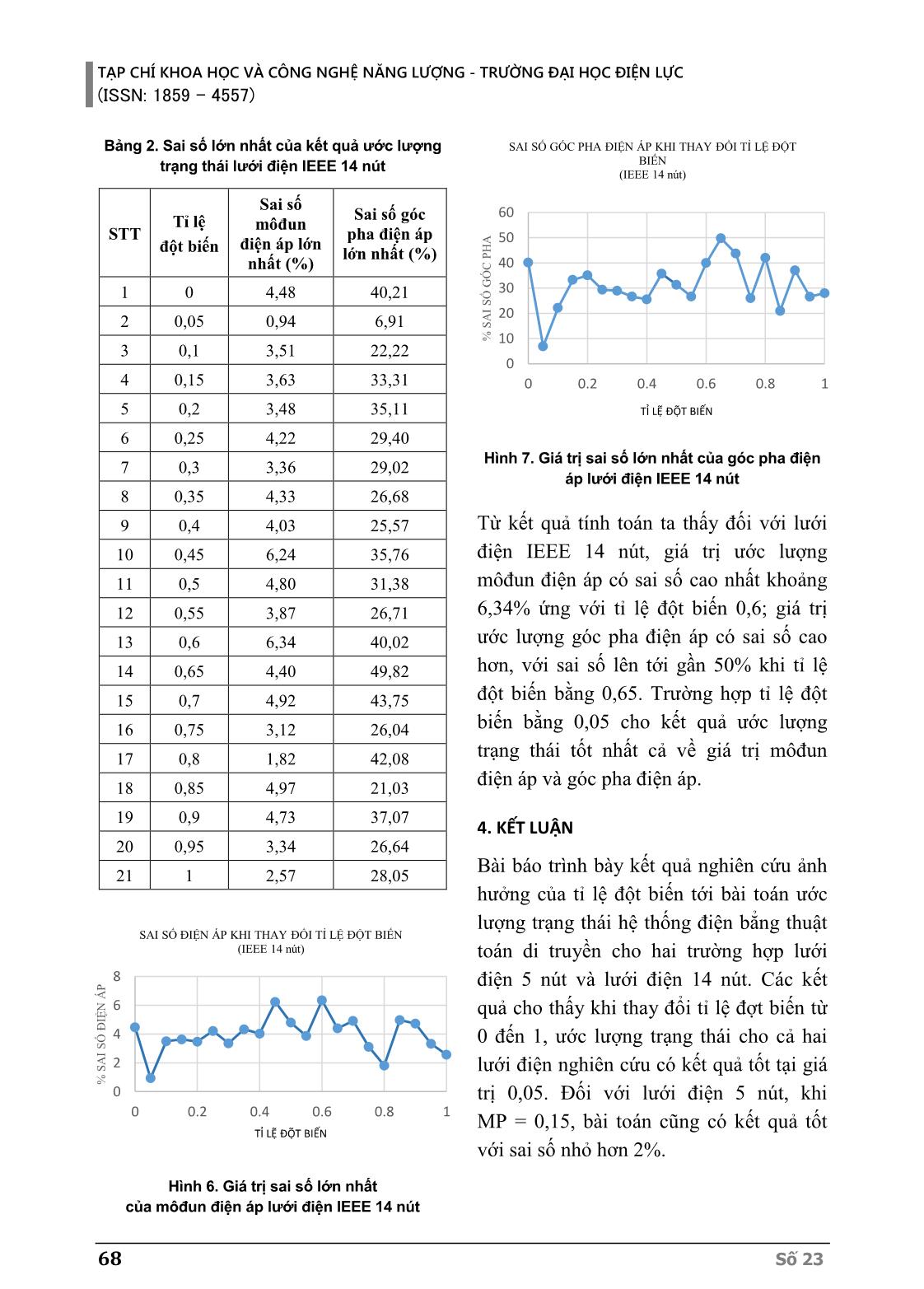
 quần thể 
gồm 𝑁 cá thể, mỗi cá thể gồm 𝑛 gen (số 
lượng biến trạng thái). Giá trị của biến 
Pi =Ui U j Gij cosqij + Bij sinqij( )
j=1
n
å
Qi =Ui U j Gij sinqij - Bij cosqij( )
j=1
n
å
Pij =Ui
2 gij + gsi( ) -UiU j gij cosqij + bij sinqij( )
Qij = -Ui
2 bij + bsi( ) -UiU j gij sinqij - bij cosqij( )
Iij = gij
2 + bij
2( ) Ui2 +U j2 - 2UiU j cosqij( )
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 65 
trạng thái trong từng cá thể sẽ được khởi 
tạo ngẫu nhiên và có giá trị nằm trong 
khoảng giới hạn của biến trạng thái. 
2.2. Lựa chọn cá thể [23] 
Việc lựa chọn cá thể sẽ được thực hiện 
theo phương pháp bánh xe Roulette. Theo 
phương pháp này, xác suất một cá thể 𝑖 
được lựa chọn sẽ tỉ lệ với giá trị hàm mục 
tiêu 𝐹𝑖 của nó: 
𝑝𝑖 =
𝐹𝑖
∑ 𝐹𝑗
𝑁
𝑗=1
 (12) 
2.3. Phép lai ghép đại số [24] 
Trong phép lai ghép đại số, hai cá thể con 
sẽ được tạo thành từ một cặp cá thể bố 
mẹ. Xét cặp cá thể bố mẹ ký hiệu là 𝐵 và 
𝑀 có chuỗi gen như sau: 
𝐵 = [𝐵1, 𝐵2, . . . , 𝐵𝑛] (13) 
𝑀 = [𝑀1, 𝑀2, . . . , 𝑀𝑛] 
Khi đó, hai cá thể con 𝐶1 và 𝐶2 được tạo 
thành dựa trên thông tin của cá thể bố mẹ 
theo công thức : 
𝐶1 = 𝛽. 𝐵 + (1 − 𝛽). 𝑀 
𝐶2 = (1 − 𝛽). 𝐵 + 𝛽. 𝑀 
(14) 
𝛽 nhận giá trị trong khoảng (0, 1). 
Khi thực hiện lai ghép, số điểm lai ghép 
có thể chọn bằng 1, 2 hoặc nhiều điểm lai 
ghép. Nếu số điểm bằng số biến trạng thái 
thì khi đó cá thể con sẽ được tạo thành 
theo công thức (14). Giá trị của 𝛽 có thể 
chọn cố định hoặc khác nhau đối với các 
biến trạng thái. 
Với thuật toán đề cập trong bài báo này, 
thay vì việc chọn 1 hay 2 điểm lai ghép, 
nhóm tác giả lựa chọn kết hợp với phép 
lai ghép đồng nhất, cụ thể là sẽ xét từng 
gen trong cá thể bố mẹ và lựa chọn có hay 
không việc thực hiện trao đổi thông tin để 
tạo thành cá thể con. 
Đầu tiên, để xét xem có thực hiện hay 
không việc trao đổi thông tin của gen bố 
mẹ, một chuỗi gen mẫu 𝐺 có biến nhận 
giá trị 0 hoặc 1 được tạo ra: 
𝐺 = [𝐺1, 𝐺2, . . . , 𝐺𝑛] (15) 
Nếu ứng với biến trạng thái 𝑖 có giá trị 
𝐺𝑖 = 1 thì gen thứ 𝑖 trong cá thể con được 
tạo thành theo công thức sau: 
𝐶1𝑖 = 𝛽𝑖. 𝐵𝑖 + (1 − 𝛽𝑖). 𝑀𝑖 
𝐶2𝑖 = (1 − 𝛽𝑖). 𝐵𝑖 + 𝛽𝑖. 𝑀𝑖 
(16) 
Trong đó giá trị 𝛽𝑖 được tạo ngẫu nhiên 
cho từng biến trạng thái 𝑖 và có giá trị 
nằm trong khoảng (0, 1). 
Nếu ứng với biến trạng thái 𝑖 có giá trị 
𝐺𝑖=0 thì gen thứ 𝑖 trong cá thể con sẽ giữ 
nguyên thông tin từ cá thể bố mẹ và được 
tạo thành theo công thức sau: 
𝐶1𝑖 = 𝐵𝑖 
𝐶2𝑖 = 𝑀𝑖 
(17) 
2.4. Đột biến [21] 
Thuật toán CGA có thể hội tụ đến giá trị 
cực trị địa phương thay vì giá trị cực trị 
toàn cục, để tránh điều này phép toán đột 
biến được thực hiện để tác động đến giá 
trị biến trạng thái bằng cách ngẫu nhiên 
thay đổi giá trị của một số biến. Điều này 
sẽ làm tăng không gian tìm kiếm và tránh 
được vấn đề hội tụ sớm. Phép đột biến có 
thể được thực hiện theo những bước sau: 
 Chọn tỉ lệ đột biến. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
66 Số 23 
 Chọn ngẫu nhiên vị trí đột biến theo tỉ 
lệ đột biến đã chọn. 
 Kiểm tra vị trí đột biến để đảm bảo 
không thực hiện đột biến với cá thể có giá 
trị hàm thích nghi tốt nhất nhằm không 
loại bỏ nghiệm của bài toán. 
 Thay giá trị biến tại vị trí đã chọn bằng 
một giá trị ngẫu nhiên nằm trong khoảng 
giới hạn của biến trạng thái. 
2.5. Điều kiện dừng lặp 
Dừng lặp được xác định theo một trong 
hai điều kiện sau: 
 Điều kiện 1: Số bước lặp tối đa. 
 Điều kiện 2: giá trị hàm mục tiêu sau 
300 bước liên tiếp không thay đổi. 
3. ẢNH HƯỞNG CỦA TỈ LỆ ĐỘT BIẾN 
TỚI KẾT QUẢ ƯỚC LƯỢNG TRẠNG 
THÁI HỆ THỐNG ĐIỆN BẰNG THUẬT 
TOÁN DI TRUYỀN 
Để xét ảnh hưởng của tỉ lệ đột biến tới tới 
kết quả ước lượng trạng thái hệ thống 
điện bằng thuật toán di truyền, ta thực 
hiện tính toán ước lượng trạng thái lưới 
điện 5 nút và IEEE 14 nút với 21 giá trị 
của tỉ lệ đột biến thay đổi từ 0 đến 1 với 
khoảng cách đều nhau và bằng 0,05. Với 
mỗi một tỉ lệ đột biến ta thực hiện 05 
phép mô phỏng và chọn ra kết quả tính 
toán tốt nhất. 
3.1. Bài toán 5 nút 
Lưới điện 5 nút có sơ đồ như trên hình 2, 
các thông số của lưới điện được lấy từ 
[25], thông số đầu vào của bài toán được 
lấy từ kết quả tính toán dòng công suất. 
Hình 2. Sơ đồ một sợi lưới điện 5 nút 
Sai số lớn nhất của kết quả mô phỏng cho 
lưới điện 5 nút tương ứng với 21 giá trị tỉ 
lệ đột biến được trình bày trong bảng 1 và 
được vẽ trên hình 3, hình 4. 
Bảng 1. Sai số lớn nhất của kết quả ước lượng 
trạng thái lưới điện 5 nút 
STT 
Tỉ lệ 
đột biến 
Sai số môđun 
điện áp 
lớn nhất (%) 
Sai số góc pha 
điện áp lớn 
nhất (%) 
1 0 1,757 19,817 
2 0,05 0,592 1,626 
3 0,1 0,566 8,061 
4 0,15 0,862 1,037 
5 0,2 0,992 2,875 
6 0,25 1,178 3,210 
7 0,3 0,335 7,508 
8 0,35 1,810 14,664 
9 0,4 1,069 10,011 
10 0,45 0,200 5,296 
11 0,5 0,196 18,278 
12 0,55 2,210 7,020 
13 0,6 0,598 10,522 
14 0,65 1,224 14,380 
15 0,7 0,853 4,434 
16 0,75 0,568 8,003 
17 0,8 1,325 23,634 
18 0,85 0,965 5,552 
19 0,9 0,261 6,179 
20 0,95 1,752 4,217 
21 1 0,989 5,770 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 67 
Hình 3. Giá trị sai số lớn nhất của modun điện 
áp lưới điện 5 nút 
Hình 4. Giá trị sai số lớn nhất của góc pha điện 
áp lưới điện 5 nút 
Từ kết quả tính toán cho lưới điện 5 nút ta 
thấy giá trị ước lượng môđun điện áp có 
sai số lớn nhất khoảng 2,2% ứng với tỉ lệ 
đột biến 0,55; giá trị ước lượng góc pha 
điện áp có sai số cao hơn, với sai số 
khoảng 23,6% khi tỉ lệ đột biến là 0,8. 
Trường hợp tỉ lệ đột biến bằng 0,05 và 
0,15, kết quả ước lượng có sai số góc pha 
lần lượt là khoảng 1,6% và 1,03%; môđun 
điện áp có sai số nhỏ hơn 0,6%. Trường 
hợp tỉ lệ đột biến bằng 0,45 và 0,5 có sai 
số môđun điện áp khoảng 0,2% nhưng sai 
số góc pha tương ứng là khoảng 5,3% và 
18,28%. Qua kết quả mô phỏng như đã 
trình bày, ta thấy khi sử dụng tỉ lệ đột 
biến bằng 0,05 và 0,15 bài toán có kết quả 
ước lượng môđun điện áp và góc pha điện 
áp tốt hơn so với các trường hợp khác, với 
sai số nhỏ hơn 2%. 
3.2. Lưới điện IEEE 14 nút 
Hình 5 thể hiện sơ đồ của lưới điện IEEE 
14 nút. Các thông số của lưới được lấy từ 
[11]. 
Sai số lớn nhất của kết quả mô phỏng cho 
lưới điện IEEE 14 nút tương ứng với 21 
giá trị tỉ lệ đột biến được trình bày trong 
bảng 2 và được vẽ trên hình 6, hình 7. 
Hình 5. Sơ đồ một sợi lưới điện IEEE 14 nút [1] 
0.0
1.0
2.0
3.0
0 0.2 0.4 0.6 0.8 1
%
 S
A
I 
S
Ố
 Đ
IỆ
N
 Á
P
TỈ LỆ ĐỘT BIẾN 
SAI SỐ ĐIỆN ÁP KHI THAY ĐỔI TỈ LỆ ĐỘT BIẾN 
(5 nút) 
0
10
20
30
0.00 0.20 0.40 0.60 0.80 1.00
%
 S
A
I S
Ố
 G
Ó
C
 P
H
A
TỈ LỆ ĐỘT BIẾN 
SAI SỐ GÓC PHA ĐIỆN ÁP KHI THAY ĐỔI TỈ LỆ ĐỘT 
BIẾN 
(5 nút) 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
68 Số 23 
Bảng 2. Sai số lớn nhất của kết quả ước lượng 
trạng thái lưới điện IEEE 14 nút 
STT 
Tỉ lệ 
đột biến 
Sai số 
môđun 
điện áp lớn 
nhất (%) 
Sai số góc 
pha điện áp 
lớn nhất (%) 
1 0 4,48 40,21 
2 0,05 0,94 6,91 
3 0,1 3,51 22,22 
4 0,15 3,63 33,31 
5 0,2 3,48 35,11 
6 0,25 4,22 29,40 
7 0,3 3,36 29,02 
8 0,35 4,33 26,68 
9 0,4 4,03 25,57 
10 0,45 6,24 35,76 
11 0,5 4,80 31,38 
12 0,55 3,87 26,71 
13 0,6 6,34 40,02 
14 0,65 4,40 49,82 
15 0,7 4,92 43,75 
16 0,75 3,12 26,04 
17 0,8 1,82 42,08 
18 0,85 4,97 21,03 
19 0,9 4,73 37,07 
20 0,95 3,34 26,64 
21 1 2,57 28,05 
Hình 6. Giá trị sai số lớn nhất 
của môđun điện áp lưới điện IEEE 14 nút 
Hình 7. Giá trị sai số lớn nhất của góc pha điện 
áp lưới điện IEEE 14 nút 
Từ kết quả tính toán ta thấy đối với lưới 
điện IEEE 14 nút, giá trị ước lượng 
môđun điện áp có sai số cao nhất khoảng 
6,34% ứng với tỉ lệ đột biến 0,6; giá trị 
ước lượng góc pha điện áp có sai số cao 
hơn, với sai số lên tới gần 50% khi tỉ lệ 
đột biến bằng 0,65. Trường hợp tỉ lệ đột 
biến bằng 0,05 cho kết quả ước lượng 
trạng thái tốt nhất cả về giá trị môđun 
điện áp và góc pha điện áp. 
4. KẾT LUẬN 
Bài báo trình bày kết quả nghiên cứu ảnh 
hưởng của tỉ lệ đột biến tới bài toán ước 
lượng trạng thái hệ thống điện bẳng thuật 
toán di truyền cho hai trường hợp lưới 
điện 5 nút và lưới điện 14 nút. Các kết 
quả cho thấy khi thay đổi tỉ lệ đợt biến từ 
0 đến 1, ước lượng trạng thái cho cả hai 
lưới điện nghiên cứu có kết quả tốt tại giá 
trị 0,05. Đối với lưới điện 5 nút, khi 
MP = 0,15, bài toán cũng có kết quả tốt 
với sai số nhỏ hơn 2%. 
0
2
4
6
8
0 0.2 0.4 0.6 0.8 1
%
 S
A
I 
S
Ố
 Đ
IỆ
N
 Á
P
TỈ LỆ ĐỘT BIẾN 
SAI SỐ ĐIỆN ÁP KHI THAY ĐỔI TỈ LỆ ĐỘT BIẾN 
(IEEE 14 nút) 
0
10
20
30
40
50
60
0 0.2 0.4 0.6 0.8 1
%
 S
A
I 
S
Ố
 G
Ó
C
 P
H
A
TỈ LỆ ĐỘT BIẾN 
SAI SỐ GÓC PHA ĐIỆN ÁP KHI THAY ĐỔI TỈ LỆ ĐỘT 
BIẾN 
(IEEE 14 nút) 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 69 
TÀI LIỆU THAM KHẢO 
[1] J. Ducan Glover, Mulukutla S. Sarma, Thomas J. Overbye, Power System Analysis and Design, 
Cengage Learning, 2011. 
[2] Schweppe F.C. and Wildes J., "Power System Static-State Estimation, Part I: Exact Model," IEEE 
Transactions on Power Apparatus and Systems, Vols. PAS-89, pp. 120-125, 1970. 
[3] Schweppe F.C. and Rom D.B., "Power System Static-State Estimation, Part II: Approximate 
Model," IEEE Transactions on Power Apparatus and Systems, Vols. PAS-89, pp. 125-130, 1970. 
[4] Schweppe F.C., "Power System Static-State Estimation, Part III: Implementation", IEEE 
Transactions on Power Apparatus and Systems, Vols. PAS-89, pp. 130-135, 170. 
[5] Dy Liaco T.E., "The Role and Implementation of State Estimation in an Energy Management 
System", International journal of Electrical Power & Energy Systems, vol. 12, no. 2, pp. 75-79, 
1990. 
[6] L. Holten, A. Gjelsvik, S. Aam, F.F. Wu and W. -. E. Liu, "Comparison of different methods for 
state estimation," IEEE Transactions on Power Systems, Vols. 3, no. 4, pp. 1798-1806, 1988. 
[7] A. Monticelli, "Electric Power System State Estimation", Proceedings of the IEEE, Vols. 88, no. 2, 
pp. 262-282, 2000. 
[8] A. Garcia, A. Monticelli, A. Abreu, "Fast Decoupled State Estimation and Bad Data Processing", 
IEEE Transactions on Power Apparatus and Systems, Vols. PAS-98, no. 5, pp. 1645-1652, 1979. 
[9] H. Dag, F.L. Alvarado, "Toward Improved Uses of the Conjugate Gradient Method for Power 
System Applications", IEEE Transactions on Power Apparatus and Systems, Vols. 12, no. 3, pp. 
1306-1314, 1997. 
[10] Dhadbanjan, Thukaram & Seshadri Sravan Kumar, V., "Linear Programming Approach for Power 
System State Estimation Using Upper Bound Optimization Techniques," International Journal of 
Emerging Electric Power Systems, pp. 11. 10.2202/1553-779X.2464., 2010. 
[11] Trần Thanh Sơn, Đặng Thu Huyền, Kiều Thị Thanh Hoa, "Ảnh hưởng của loại và vị trí phép đo tới 
kết quả ước lượng trạng thái hệ thống điện bằng thuật toán tối ưu bầy đàn," Tạp chí Khoa học và 
công nghệ năng lượng - Trường đại học Điện lực, vol. 19, pp. 1-8, 2018. 
[12] D.H. Tungadio, J.A. Jordaan, M.W. Siti, "Power System State Estimation Solution using Modified 
Models of PSO Algorithm: Comparative Study", Measurement, 2016. 
[13] D.H. Tungadio, Jacobus A. Jordaan, Willy Mukwanga Siti, B.P. Numbi, "Weighted Least Squares 
and Iteratively Reweighted Least Square Comparison Using Particle Swam Optimization Algorithm 
in Solving Power System State Estimation," in Africon, Mauritius, 2013. 
[14] D.H. Tungadio, BP Numbi, M.W. Siti, A.A. Jimoh, "Particle Swarm Optimization for Power System 
State Estimation," Neurocomputing, p. 148. 10.1016/j.neucom.2012.10.049., 2014. 
[15] F. Aminifar, C. Lucas, A. Khodaei and M. Fotuhi-Firuzabad, "Optimal Placement of Phasor 
Measurement Units Using Immunity Genetic Algorithm", IEEE Transactions on Power Delivery, 
Vols. 24, no. 3, pp. 1014-1020, 2009. 
[16] T. Kerdchuen and W. Ongsakul, "Optimal Measurement Placement for Power System State 
Estimation Using Hybrid Genetic Algorithm and Simulated Annealing", in International Conference 
on Power System Technology, Chongqing, 2006. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
70 Số 23 
[17] A. Kumar, B. Das and J. Sharma, "Genetic Algorithm-based Meter Placement for Static Estimation 
of Harmonic Sources," IEEE Transactions on Power Delivery, Vols. 20, no. 2, pp. 1088-1096, 
2005. 
[18] F. Aminifar, C. Lucas, A. Khodaei and M. Fotuhi-Firuzabad, "Optimal Placement of Phasor 
Measurement Units Using Immunity Genetic Algorithm", IEEE Transactions on Power Delivery, 
Vols. 24, no. 3, pp. 1014-1020, 2009. 
[19] H.H. Müller and C.A. Castro, "Genetic Algorithm-based Phasor Measurement Unit Placement 
Method Considering Observability and Security Criteria", ET Generation, Transmission & 
Distribution, Vols. 10, no. 1, pp. 270-280, 2016. 
[20] A.A. Hosam-Eldin, E.N. Abdallah, M.S. El-Nozahy, "A Modified Genetic Based Tecnique for Solving 
the Power System State Estimation Problem", World Academy of Science, Engineering and 
Technology International Journal of Electrical and Computer Engineering, vol. 3, no. 7, 2009. 
[21] Randy L. Haupt, Sue Ellen Haupt, Pratical Genetic Algorithm, Hoboken, New Jersey: John Wiley & 
Sons, 2004. 
[22] Pencheva T., Atanassov K., Shannon A., "Modelling of a Roulette Wheel Selection Operator in 
Genetic Algorithms Using Generalized Nets", Bioautomation, vol. 13, pp. 257-264, 2009. 
[23] S.S. Rao, Enginerring Optimization - Theory and Practice, Hoboken, New Jersey: John Wiley & 
Sons, 2009. 
[24] Z. Michalewicz, Genetic Algorithms + Data Structures = Evolution Programs, New York: Springer-
Verlag, 1994. 
Giới thiệu tác giả: 
Tác giả Trần Thanh Sơn tốt nghiệp Trường Đại học Bách khoa Hà Nội chuyên 
ngành hệ thống điện năm 2004; nhận bằng Thạc sĩ chuyên ngành kỹ thuật điện tại 
Đại học Bách khoa Grenoble, Cộng hoà Pháp năm 2005; nhận bằng Tiến sĩ chuyên 
ngành kỹ thuật điện của Đại học Joseph Fourier - Cộng hoà Pháp năm 2008. Hiện 
nay tác giả là Trưởng khoa Kỹ thuật điện, Trường Đại học Điện lực. 
Lĩnh vực nghiên cứu: ứng dụng phương pháp số trong tính toán, mô phỏng trường 
điện từ, các bài toán tối ưu hoá trong hệ thống điện, lưới điện thông minh. 
Tác giả Kiều Thị Thanh Hoa tốt nghiệp Trường Đại học Điện lực chuyên ngành kỹ 
thuật điện năm 2011; nhận bằng Thạc sĩ chuyên ngành kỹ thuật điện - chương 
trình liên kết đào tạo giữa Trường Đại học Điện lực và Đại học Palermo năm 2014. 
Hiện nay tác giả là giảng viên Trường Đại học Điện lực. 
Lĩnh vực nghiên cứu: tính toán chế độ hệ thống điện, ước lượng trạng thái hệ 
thống, điều khiển kết nối nguồn phân tán. 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ NĂNG LƯỢNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC 
(ISSN: 1859 - 4557) 
Số 23 71