Ảnh hưởng của liên kết Spin quỹ đạo lên tính chất điện tử của mos2 đơn lớp

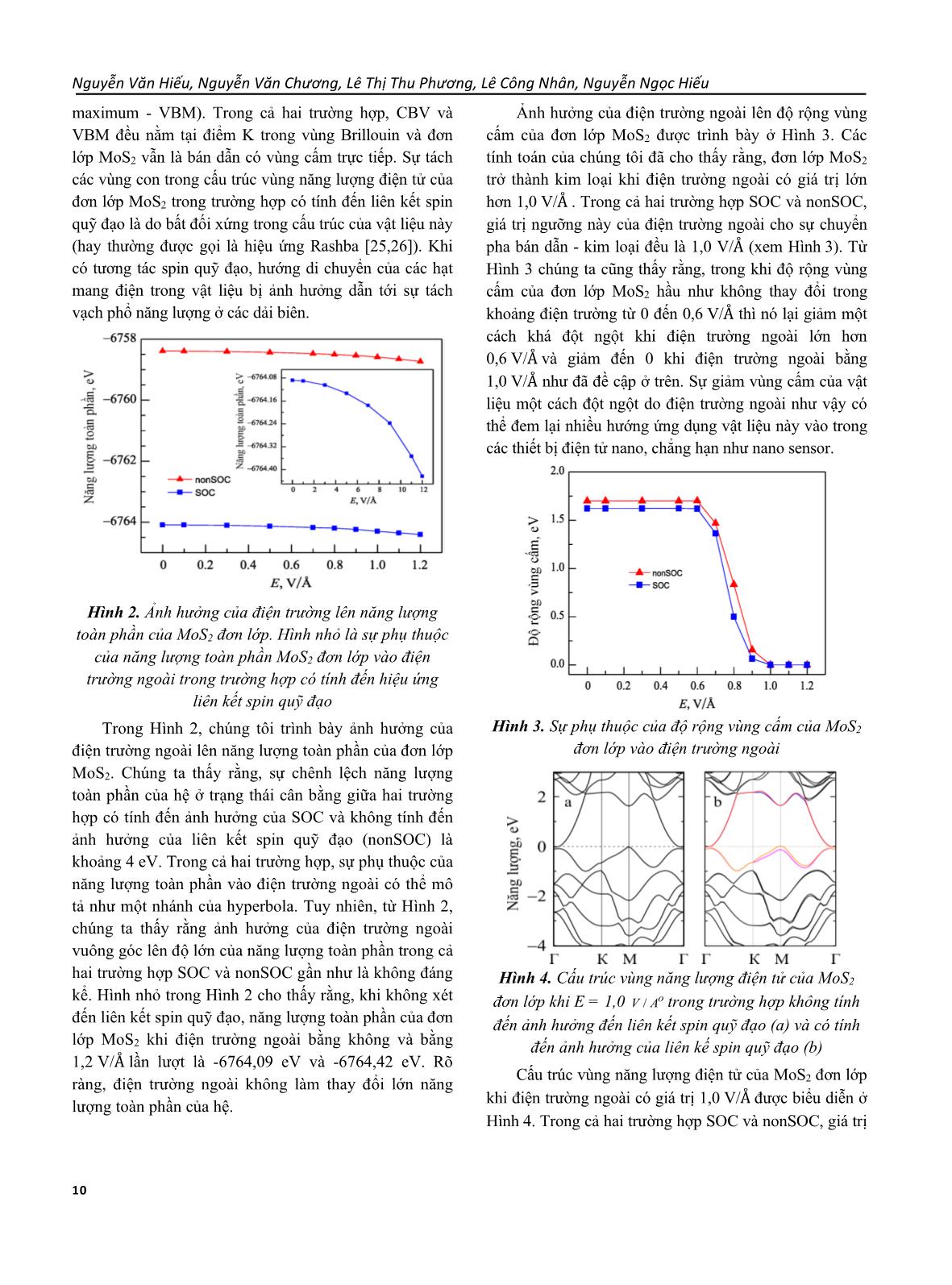
ện trường 
ngoài. Bên cạnh đó, ảnh hưởng của áp suất cao lên cấu 
trúc nguyên tử, các trạng thái điện tử và tính chất nhiệt 
 ISSN 1859 - 4603 - Tạp chí Khoa học Xã hội, Nhân văn & Giáo dục, Tập 8, số 4 (2018), 8-12 
 9 
điện của một số kim loại chuyển tiếp dichalcogenide 
MX2 cũng đã được nghiên cứu bằng phương pháp lí 
thuyết phiếm hàm mật độ [16,18]. 
Trong bài báo này, chúng tôi nghiên cứu ảnh hưởng 
của liên kết spin quỹ đạo (spin-orbit coupling - SOC) 
lên tính chất điện tử của MoS2 đơn lớp khi có mặt của 
điện trường ngoài bằng lí thuyết phiếm hàm mật độ 
(density functional theory - DFT). Chúng tôi khảo sát 
ảnh hưởng của SOC lên cấu trúc vùng năng lượng điện 
tử và sự phụ thuộc của độ rộng vùng cấm vào điện 
trường ngoài của đơn lớp MoS2. 
2. Mô hình và phương pháp tính toán 
Trong bài báo này, chúng tôi khảo sát MoS2 đơn 
lớp đặt trong điện trường vuông góc với mặt phẳng 
MoS2. Chúng tôi sử dụng phương pháp lí thuyết phiếm 
hàm mật độ (density functional theory - DFT) bằng cách 
sử dụng gần đúng gradient tổng quát (generalized 
gradient approximation - GGA) đối với năng lượng trao 
đổi tương quan [19,20]. Các tính toán được thực hiện 
dựa trên mã nguồn Quantum Espresso [21]. Hàm sóng 
điện tử được mô tả bằng tập hợp các sóng phẳng với 
năng lượng ngưỡng bằng 30 Ry (xấp xỉ 400 eV). Để 
khảo sát chính xác các tương tác van der Waals (có thể 
tồn tại giữa các lớp Mo và S trong MoS2 đơn lớp), 
chúng tôi đã sử dụng phương pháp DFT-D2 được đề 
xuất bởi Grimme [22]. Bên cạnh đó, một khoảng chân 
không bằng 20 Å theo phương vuông góc với bề mặt hai 
chiều của vật liệu đã được sử dụng để tránh các tương 
tác giữa các đơn lớp liền kề nhau trong quá trình tính 
toán. Chúng tôi đã sử dụng thành công phương pháp 
này để tính toán cho MoS2 và một số hệ có cấu trúc 
tương tự [23,24]. Khi khảo sát ảnh hưởng của điện 
trường ngoài lên tính chất điện tử của vật liệu, điện 
trường ngoài có cường độ từ 0 đến 1,2 V/Å đã được áp 
đặt vuông góc với bề mặt hai chiều của vật liệu. 
3. Kết quả và thảo luận 
Để khảo sát ảnh hưởng của liên kết spin quỹ đạo 
(SOC) lên tính chất điện tử của đơn lớp MoS2, trước 
tiên chúng tôi tính toán cấu trúc vùng năng lượng của 
đơn lớp MoS2 cho cả trường hợp có xét đến ảnh hưởng 
của liên kết spin quỹ đạo (SOC) và không xét đến ảnh 
hưởng của liên kết spin quỹ đạo (nonSOC). Các tính 
toán của chúng tôi cho thấy rằng, khi không tính đến 
ảnh hưởng của liên kết spin quỹ đạo, đơn lớp MoS2 là 
bán dẫn có vùng cấm trực tiếp với độ rộng vùng cấm là 
1,70 eV [10]. 
Hình 1. Cấu trúc vùng năng lượng điện tử của MoS2 
đơn lớp ở trạng thái cân bằng trong trường hợp không 
tính đến (a) và có tính đến (b) tương tác spin quỹ đạo 
Hình 1 trình bày cấu trúc vùng năng lượng điện tử 
của đơn lớp MoS2 cho cả hai trường hợp có và không có 
ảnh hưởng của liên kết spin quỹ đạo. Với trường hợp 
không tính đến ảnh hưởng của liên kết spin quỹ đạo 
[Hình 1(a)], chúng ta thấy rằng, cực đại của vùng hóa trị 
và cực tiểu của vùng dẫn nằm tại điểm K trong vùng 
Brillouin thứ nhất. Trong công trình trước đây [10], 
chúng tôi đã chỉ ra rằng, cực tiểu vùng dẫn được đóng 
góp chủ yếu từ các orbital Mo–d trong khi cực đại vùng 
hóa trị thì được đóng góp chủ yếu từ các orbital Mo–d 
và S–p. Các orbital Mo–d và S–p lai hóa lẫn nhau tại 
đỉnh của vùng hóa trị. Khi xét đến SOC, các tính toán 
của chúng tôi đã chỉ ra rằng, đơn lớp MoS2 vẫn là bán 
dẫn với vùng cấm trực tiếp với độ rộng bằng 1,62 eV 
[Hình 1(b)]. Trong trường hợp này, cực đại vùng hóa trị 
và cực tiểu vùng dẫn vẫn nằm tại điểm K của vùng 
Brillouin. Khi tính đến ảnh hưởng của SOC, bên cạnh 
việc vùng cấm của đơn lớp MoS2 bị thu hẹp (1,62 eV so 
với 1,70 eV trong trường hợp không tính đến SOC), từ 
Hình 1(b) chúng ta thấy một điều thú vị nữa đó là sự 
tách các vùng con ở cả vùng dẫn và vùng hóa trị lân cận 
mức Fermi. Chính sự tách các vùng con này, đặc biệt là 
ở vùng hóa trị, đã dẫn đến sự thu hẹp năng lượng vùng 
cấm của đơn lớp MoS2 trong trường hợp này so với 
trường hợp không tính đến ảnh hưởng của liên kết spin 
quỹ đạo. Tuy nhiên, ở trạng thái cân bằng, ngoài sự thay 
đổi độ rộng vùng cấm, liên kết spin quỹ đạo không làm 
thay đổi vị trí của cực tiểu vùng dẫn (conduction band 
minimum - CBM) và cực đại vùng hóa trị (valence band 
Nguyễn Văn Hiếu, Nguyễn Văn Chương, Lê Thị Thu Phương, Lê Công Nhân, Nguyễn Ngọc Hiếu 
10 
maximum - VBM). Trong cả hai trường hợp, CBV và 
VBM đều nằm tại điểm K trong vùng Brillouin và đơn 
lớp MoS2 vẫn là bán dẫn có vùng cấm trực tiếp. Sự tách 
các vùng con trong cấu trúc vùng năng lượng điện tử của 
đơn lớp MoS2 trong trường hợp có tính đến liên kết spin 
quỹ đạo là do bất đối xứng trong cấu trúc của vật liệu này 
(hay thường được gọi là hiệu ứng Rashba [25,26]). Khi 
có tương tác spin quỹ đạo, hướng di chuyển của các hạt 
mang điện trong vật liệu bị ảnh hưởng dẫn tới sự tách 
vạch phổ năng lượng ở các dải biên. 
Hình 2. Ảnh hưởng của điện trường lên năng lượng 
toàn phần của MoS2 đơn lớp. Hình nhỏ là sự phụ thuộc 
của năng lượng toàn phần MoS2 đơn lớp vào điện 
trường ngoài trong trường hợp có tính đến hiệu ứng 
liên kết spin quỹ đạo 
Trong Hình 2, chúng tôi trình bày ảnh hưởng của 
điện trường ngoài lên năng lượng toàn phần của đơn lớp 
MoS2. Chúng ta thấy rằng, sự chênh lệch năng lượng 
toàn phần của hệ ở trạng thái cân bằng giữa hai trường 
hợp có tính đến ảnh hưởng của SOC và không tính đến 
ảnh hưởng của liên kết spin quỹ đạo (nonSOC) là 
khoảng 4 eV. Trong cả hai trường hợp, sự phụ thuộc của 
năng lượng toàn phần vào điện trường ngoài có thể mô 
tả như một nhánh của hyperbola. Tuy nhiên, từ Hình 2, 
chúng ta thấy rằng ảnh hưởng của điện trường ngoài 
vuông góc lên độ lớn của năng lượng toàn phần trong cả 
hai trường hợp SOC và nonSOC gần như là không đáng 
kể. Hình nhỏ trong Hình 2 cho thấy rằng, khi không xét 
đến liên kết spin quỹ đạo, năng lượng toàn phần của đơn 
lớp MoS2 khi điện trường ngoài bằng không và bằng 
1,2 V/Å lần lượt là -6764,09 eV và -6764,42 eV. Rõ 
ràng, điện trường ngoài không làm thay đổi lớn năng 
lượng toàn phần của hệ. 
Ảnh hưởng của điện trường ngoài lên độ rộng vùng 
cấm của đơn lớp MoS2 được trình bày ở Hình 3. Các 
tính toán của chúng tôi đã cho thấy rằng, đơn lớp MoS2 
trở thành kim loại khi điện trường ngoài có giá trị lớn 
hơn 1,0 V/Å . Trong cả hai trường hợp SOC và nonSOC, 
giá trị ngưỡng này của điện trường ngoài cho sự chuyển 
pha bán dẫn - kim loại đều là 1,0 V/Å (xem Hình 3). Từ 
Hình 3 chúng ta cũng thấy rằng, trong khi độ rộng vùng 
cấm của đơn lớp MoS2 hầu như không thay đổi trong 
khoảng điện trường từ 0 đến 0,6 V/Å thì nó lại giảm một 
cách khá đột ngột khi điện trường ngoài lớn hơn 
0,6 V/Å và giảm đến 0 khi điện trường ngoài bằng 
1,0 V/Å như đã đề cập ở trên. Sự giảm vùng cấm của vật 
liệu một cách đột ngột do điện trường ngoài như vậy có 
thể đem lại nhiều hướng ứng dụng vật liệu này vào trong 
các thiết bị điện tử nano, chẳng hạn như nano sensor. 
Hình 3. Sự phụ thuộc của độ rộng vùng cấm của MoS2 
đơn lớp vào điện trường ngoài 
Hình 4. Cấu trúc vùng năng lượng điện tử của MoS2 
đơn lớp khi E = 1,0 / oV A trong trường hợp không tính 
đến ảnh hưởng đến liên kết spin quỹ đạo (a) và có tính 
đến ảnh hưởng của liên kế spin quỹ đạo (b) 
Cấu trúc vùng năng lượng điện tử của MoS2 đơn lớp 
khi điện trường ngoài có giá trị 1,0 V/Å được biểu diễn ở 
Hình 4. Trong cả hai trường hợp SOC và nonSOC, giá trị 
 ISSN 1859 - 4603 - Tạp chí Khoa học Xã hội, Nhân văn & Giáo dục, Tập 8, số 4 (2018), 8-12 
 11 
ngưỡng của điện trường cho sự chuyển pha bán dẫn - kim 
loại đều là 1,0 V/Å (xem thêm Hình 3). Điểm thú vị khi 
xét đến liên kết spin quỹ đạo trong hệ đơn lớp MoS2 là 
sự tách vùng con ở lân cận mức Fermi trong cấu trúc 
vùng năng lượng điện tử như đã đề cập ở trên. Sự tách 
vùng này dẫn đến sự thay đổi độ rộng vùng cấm cũng 
như thay đổi vị trí của cực tiểu vùng dẫn CBM và cực 
đại vùng hóa trị VBM của đơn lớp MoS2. 
4. Kết luận 
Bằng lí thuyết phiếm hàm mật độ, chúng tôi đã 
nghiên cứu ảnh hưởng của liên kết spin quỹ đạo lên tính 
chất điện tử của MoS2 đơn lớp khi có mặt của điện 
trường ngoài. Các tính toán bằng lí thuyết phiếm hàm 
mật độ đã chỉ ra rằng, hiệu ứng liên kết spin quỹ đạo 
chẳng những làm thay đổi độ rộng vùng cấm của MoS2 
đơn lớp mà còn làm xuất hiện sự tách các vùng con 
năng lượng ở lân cận mức Fermi. Sự chuyển pha bán 
dẫn–kim loại đã được tìm thấy trong MoS2 đơn lớp và 
giá trị ngưỡng của điện trường ngoài cho sự chuyển pha 
này cũng đã được xác định. 
Lời cảm ơn: Nghiên cứu này được tài trợ bởi 
Trường ĐHSP, ĐH Đà Nẵng trong đề tài trọng điểm mã 
số T2018-TĐ-03-01. 
Tài liệu tham khảo 
[1] K.S. Novoselov, A.K. Geim, S.V. Morozov, D. 
Jiang, Y. Zhang, S.V. Dubonos, I.V. Grigorieva, 
A.A. Firsov (2004). Electric field effect in 
atomically thin carbon films. Science, 306 (5696), 
666-669. 
[2] E.P. Randviir, D.A.C. Brownson, C.E. Banks 
(2014. A decade of graphene research: production, 
applications and outlook. Materials Today, 17(9), 
426-432. 
[3] F. Schwierz (2010). Graphene transistors. Nature 
Nanotechnology, 5, 487-496. 
[4] T.C. Berkelbach, M.S. Hybertsen, D.R. Reichman 
(2013). Theory of neutral and charged excitons in 
monolayer transition metal dichalcogenides. 
Physical Review B, 88, 045318-045323. 
[5] K.F. Mak, C. Lee, J. Hone, J. Shan, T.F. Heinz 
(2010). Atomically thin MoS2: A new direct-gap 
semiconductor. Physical Review Letters, 105, 
136805 (4 pages). 
[6] K.S. Novoselov, D. Jiang, F. Schedin, T.J. Booth, 
V.V. Khotkevich, S.V. Morozov, A.K. Geim (2005). 
Two-dimensional atomic crystals. Proceedings of 
the National Academy of Sciences of the United 
States of America, 102(30), 10451-10453. 
[7] R. Ganatra, Q. Zhang (2014). Few-layer MoS2: A 
promising layered semiconductor. ACS Nano, 8, 
4074-4099. 
[8] J.N. Coleman, M. Lotya, A. O’Neill, S.D. Bergin, 
P.J. King, U. Khan, K. Young, A. Gaucher, S. De, 
R.J. Smith, I.V. Shvets, S.K. Arora, G. Stanton, 
H.Y. Kim, K. Lee, G.T. Kim, G.S. Duesberg, T. 
Hallam, J.J. Boland, J.J. Wang, J.F. Donegan, J.C. 
Grunlan, G. Moriarty, A. Shmeliov, R.J. Nicholls, 
J.M. Perkins, E.M. Grieveson, K. Theuwissen, D.W. 
McComb, P.D. Nellist, V. Nicolosi (2011). Two-
dimensional nanosheets produced by liquid 
exfoliation of layered materials. Science, 331(6017), 
568-571. 
[9] D. Kim, D. Sun, W. Lu, Z. Cheng, Y. Zhu, D. Le, 
T.S. Rahman, L. Bartels (2011). Toward the growth 
of an aligned single-layer MoS2 film. Langmuir, 
27(18), 11650-11653. 
[10] C.V. Nguyen, N.N. Hieu (2016). Effect of biaxial 
strain and external electric field on electronic 
properties of MoS2 monolayer: A first-principle 
study. Chemical Physics, 468, 9-14. 
[11] C. Ataca, M. Topsakal, E. Aktürk, S. Ciraci 
(2011). A comparative study of lattice dynamics of 
three- and two-dimensional MoS2. The Journal of 
Physical Chemistry C, 115, 16354-16361. 
[12] S. Lebègue, O. Eriksson (2009). Electronic 
structure of two-dimensional crystals from ab initio 
theory. Physical Review B, 79, 115409-115414. 
[13] P. Johari, V.B. Shenoy (2011). Tunable dielectric 
properties of transition metal dichalcogenides. ACS 
Nano. 5, 5903-5908. 
[14] P. Johari, V.B. Shenoy (2012). Tuning the 
electronic properties of semiconducting transition 
metal dichalcogenides by applying mechanical 
strains. ACS Nano, 6, 5449-5456. 
[15] U.K. Sen, P. Johari, S. Basu, C. Nayak, S. Mitra 
(2014). An experimental and computational study to 
understand the lithium storage mechanism in 
molybdenum disulfide. Nanoscale, 6, 10243-10254. 
[16] H. Guo, T. Yang, P. Tao, Y. Wang, Z. Zhang 
(2013). High pressure effect on structure, electronic 
structure, and thermoelectric properties of MoS2. 
Journal of Applied Physics, 113(1), 013709-013714. 
[17] X. Fan, C.H. Chang, W.T. Zheng, J.-L. Kuo, D.J. 
Singh (2015). The electronic properties of single-
layer and multilayer MoS2 under high pressure. The 
Journal of Physical Chemistry C, 119, 10189-10196. 
[18] O. Kohulák, R. Martoňák (2017). New high-
Nguyễn Văn Hiếu, Nguyễn Văn Chương, Lê Thị Thu Phương, Lê Công Nhân, Nguyễn Ngọc Hiếu 
12 
pressure phases of MoSe2 and MoTe2. Physical 
Review B, 95, 054105-054112. 
[19] J.P. Perdew, K. Burke, M. Ernzerhof (1996). 
Generalized gradient approximation made simple. 
Physical Review Letters, 77, 3865-3868. 
[20] J.P. Perdew, K. Burke, M. Ernzerhof (1997). 
Generalized gradient approximation made simple 
[Phys. Rev. Lett. 77, 3865 (1996)]. Physical Review 
Letters, 78, 1396-1396. 
[21] G. Paolo, B. Stefano, B. Nicola, C. Matteo, C. 
Roberto, C. Carlo, C. Davide, L.C. Guido, C. 
Matteo, D. Ismaila, C. Andrea Dal, G. Stefano de, F. 
Stefano, F. Guido, G. Ralph, G. Uwe, G. Christos, 
K. Anton, L. Michele, M.-S. Layla, M. Nicola, M. 
Francesco, M. Riccardo, P. Stefano, P. Alfredo, P. 
Lorenzo, S. Carlo, S. Sandro, S. Gabriele, P.S. Ari, 
S. Alexander, U. Paolo, M.W. Renata (2009). 
QUANTUM ESPRESSO: a modular and open-
source software project for quantum simulations of 
materials. Journal of Physics: Condensed Matter, 
21, 395502 (19 pages). 
[22] S. Grimme (2006). Semiempirical GGA‐type 
density functional constructed with a long‐range 
dispersion correction. Journal of Computatinal 
Chemistry, 27(15), 1787-1799. 
[23] N.N. Hieu, H.V. Phuc, V. V Ilyasov, N.D Chien, 
N.A Poklonski, N.V. Hieu, C.V. Nguyen (2017). 
First-principles study of the structural and electronic 
properties of graphene/MoS2 interfaces. Journal 
Applied Physics, 122, 104301 (7 pages). 
[24] H. V. Phuc, N. N. Hieu, B. D. Hoi, N. V. Hieu, T. 
V. Thu, N. M. Hung, V. V. Ilyasov, N. A. 
Poklonski, C. V. Nguyen (2018). Tuning the 
electronic properties, effective mass and carrier 
mobility of MoS2 monolayer by strain engineering: 
First-principle calculations. Journal of Electronic 
Materials, 47(1), 730-736. 
[25] Y. A. Bychkov and É. I. Rashba (1984). Properties 
of a 2D electroni gas with lifted spectral defeneracy. 
JETP Letters 39, 78-81. 
[26] A. Manchon, H. C. Koo, J. Nitta, S. M. Frolov, 
and R. A. Duine (2015). New perspectives for 
Rashba spin-orbit coupling. Nature Materials, 14, 
871-882. 
EFFECT OF SPIN-ORBIT COUPLING ON ELECTRONIC PROPERTIES 
OF MONOLAYER MoS2 
Abstract: In the present paper (article), we examine the effect of spin-orbit coupling on electronic properties of monolayer MoS2 
under an external electric field using density functional theory. Our caculations show that there is a spliting of subbands near the 
Fermi level in the electronic band structure of the monolayer MoS2 when the spin-orbit coupling effect is included. Besides, the 
semiconductor-metal phase transition has been found in the monolayer MoS2 at the external electric field of 1.0 V/Å. 
Key words: Monolayer MoS2; electronic properties; density functional theory.