Analyzing enhancement and control of kerrnonlinear coefficient in a three - level v - type inhomogeneously broadened atomic medium

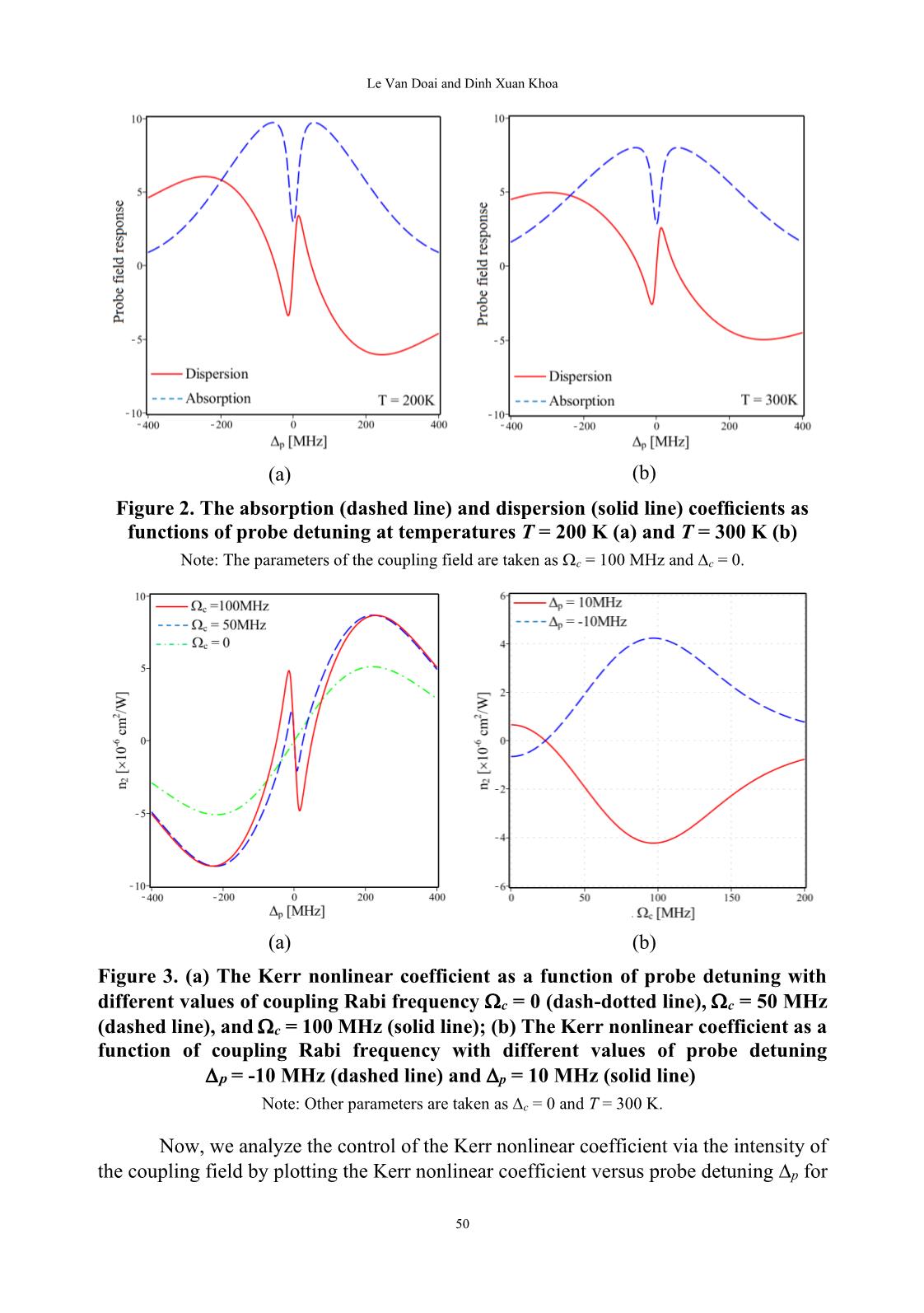
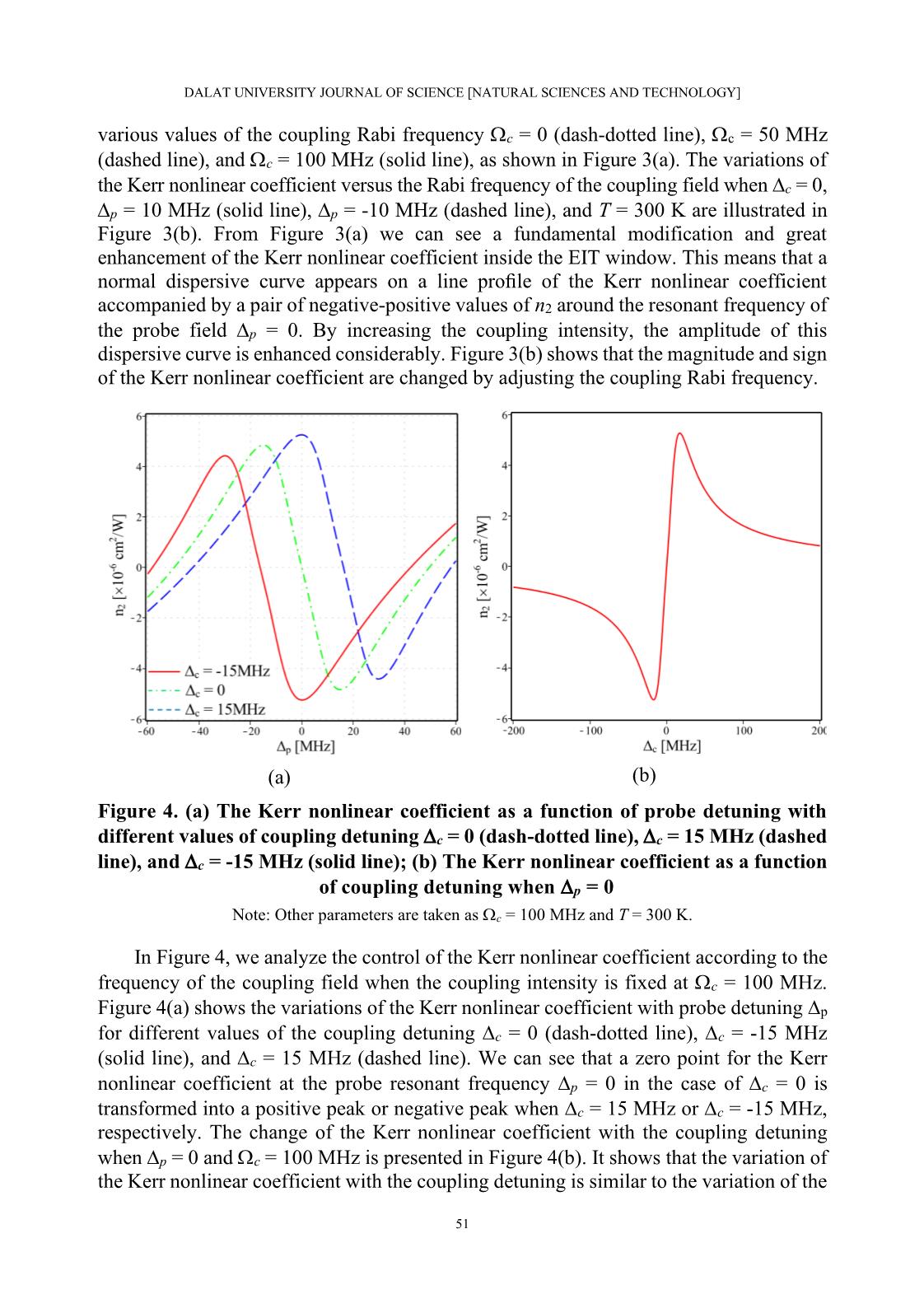
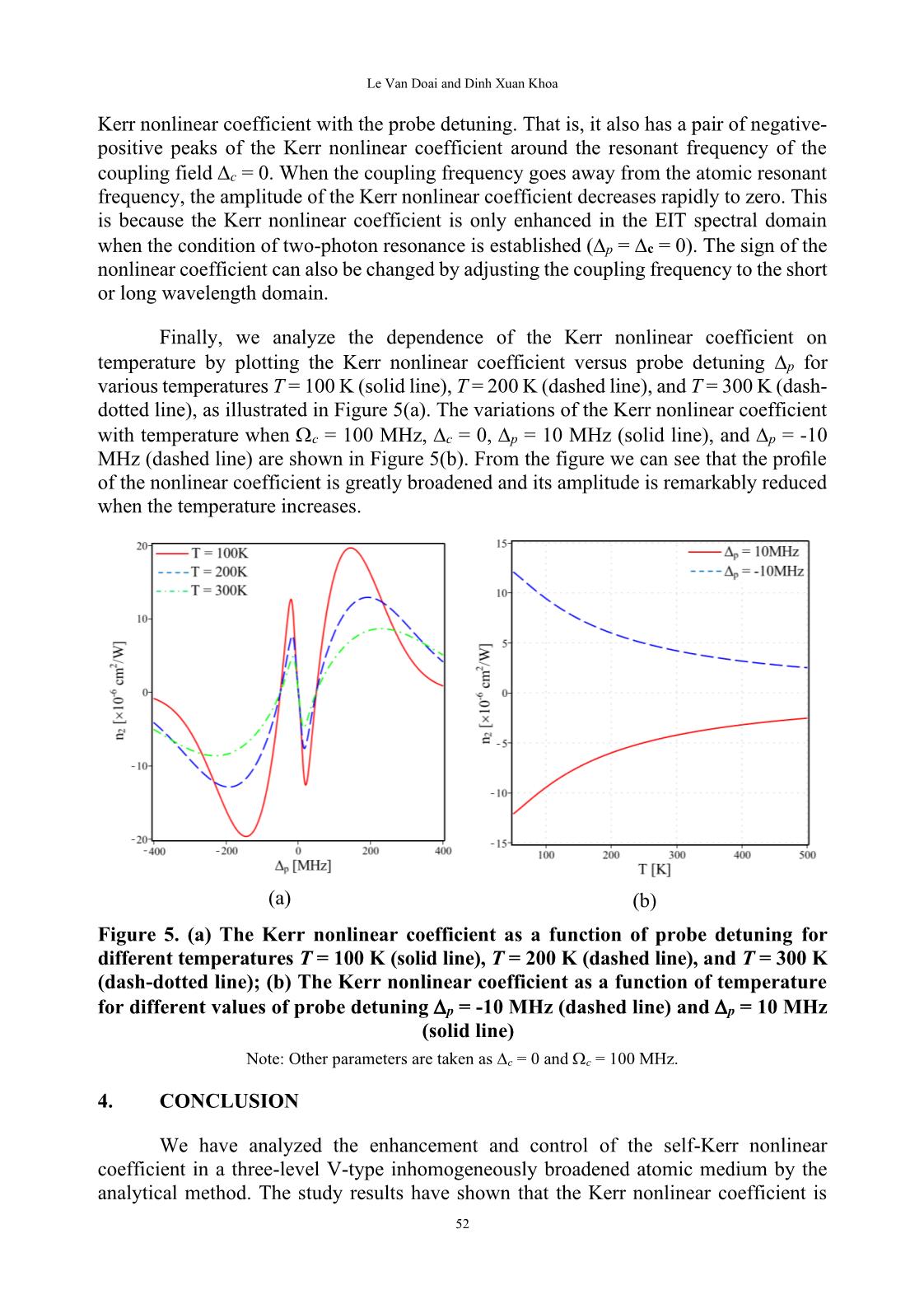
1)
21
( )
2
pi
A
 −
= , (11) 
2
(3)
21 *
21
1 1
2 2
p pi
A A A
  
= − + 
 
. (12) 
where: 
,
)(
)2/(
32
2
21
cp
c
p
i
iA
 − −

+ −=


and *A is the complex conjugation of A. The solution of the density matrix element 21 is 
calculated up to third order as: 
2
(1) (3)
21 21 21 *
21
1 1
2 2 2
p p pi i
A A A A
    
= + = − + 
 
. (14) 
(13) 
Le Van Doai and Dinh Xuan Khoa 
48 
The total susceptibility of the atomic medium is related to the density matrix 
element 21 as follows (Boyd, 2008): 
2 4
221 21 21
21 3 *
0 0 0 21
1 1 1 1
2
2
p
p
Nd iNd iNd
E
E A A A A
 
  
= −  − + 
 
. (15) 
The total susceptibility can be written in another way as (Boyd, 2008): 
(1) 2 (3)3 pE  = + . (16) 
Comparing Equations (15) and (16) we obtain the first- and third-order 
susceptibilities as follows: 
2
(1) 21
0
1iNd
A


= , (17) 
4
(3) 21
3 *
0 21
1 1 1 1
3 2
iNd
A A A


= − + 
 
. (18) 
Now we study the effect of Doppler broadening on the first- and third-order 
susceptibilities. To eliminate the first-order Doppler effect, we consider the probe and 
coupling beams co-propagating inside the medium. Therefore, an atom moving with 
velocity v in the propagation direction of the probe beam will see an upshift frequency of 
the probe and coupling laser as ( / )p pv c + and ( / )c cv c + , respectively. Therefore, 
the susceptibility expressions must be modified to 
2 22 /
(1) 0 21
0
( )
( )
v uiN d e
v dv dv
A vu

 
−
= , (19) 
2 24 /
(3) 0 21
*3
0
1 1
( )
( ) ( ) ( )3
v uiN d e
v dv dv
A v A v A vu

 
− 
= − + 
, (20) 
where 2 /Bu k T m= is the root mean square atomic velocity, N0 is the total atomic density 
of the atomic medium, and 
2
21
32
/ 4
( )
( ) ( )
c
p p
p c p c
v
A v i
vc
i i
c
 
  
 
= − + + 
 − − − −
. (21) 
By integrating (19) and (20) over the velocity v from - to + , we have: 
DALAT UNIVERSITY JOURNAL OF SCIENCE [NATURAL SCIENCES AND TECHNOLOGY] 
49 
( )
2
2
(1) 0 21
0
[1 ( )]
/
a
p
iN d
e erf a
u c

 
= − , (22)
( )
4
(3) 0 21
2
3
03 /p
iN d
u c

  
= − 
 ( )
( )
2 2
2
[1 ( )] [1 ( )]
2 1 [1 ( )]
a a
a
e erf a e erf a
ae erf a
a a
 − + − 
 − + − + 
+ 
, 
where 
2
21
32
/ 4
( )
c
p
p p c p
c c
a i A
u i u

  
 
= − + = − − 
, (24) 
*a is the complex conjugation of a, and erf (a) is the error function. 
From the first- and third-order susceptibilities, we find the expressions for the 
linear index (n0) and the Kerr nonlinear coefficient n2 as (Doai et al., 2015): 
(1)
0 1 Re( )n = + , (25) 
(3)
2 2
0 0
3Re( )
4
n
n c


= . (26) 
3. RESULTS AND DISCUSSION 
The theoretical model is applied to 87Rb atomic vapor with the states |1, |2, and 
|3 chosen as 1/25 ( 1)S F = , 1/25 ( 1)P F = , and 1/25 ( 2)P F = , respectively. The atomic 
parameters are (Doai et al., 2015): N = 3.5 1017 atoms/m3, 21 = 31 = 6 MHz, 21 = 3 MHz, 
32 = 6 MHz , and d21 = 1.6 10-29 cm. 
In Figure 2 we examine the influence of Doppler broadening on the EIT and 
dispersion spectra by plotting the absorption (dashed line) and dispersion (solid line) 
coefficients versus probe detuning p at different temperatures T = 200 K (a) and T = 300 K 
(b). The parameters of the coupling field employed in Figure 2 are c = 100 MHz and 
 c = 0. It is clear that an increase in temperature leads to the depth and width of the EIT 
window being significantly reduced. Simultaneously, the amplitude of the normal 
dispersive curve inside the EIT window is reduced remarkably. We note that due to the 
decay rate between excited states in the three-level V-type system being much greater 
than that of three-level lambda-type system, the EIT effect in the V-type system occurs 
with more intensity of the coupling field. 
( 
(23) 
Le Van Doai and Dinh Xuan Khoa 
50 
(a) 
(b) 
Figure 2. The absorption (dashed line) and dispersion (solid line) coefficients as 
functions of probe detuning at temperatures T = 200 K (a) and T = 300 K (b) 
Note: The parameters of the coupling field are taken as c = 100 MHz and c = 0. 
(a) 
(b) 
Figure 3. (a) The Kerr nonlinear coefficient as a function of probe detuning with 
different values of coupling Rabi frequency c = 0 (dash-dotted line), c = 50 MHz 
(dashed line), and c = 100 MHz (solid line); (b) The Kerr nonlinear coefficient as a 
function of coupling Rabi frequency with different values of probe detuning 
 p = -10 MHz (dashed line) and p = 10 MHz (solid line) 
Note: Other parameters are taken as c = 0 and T = 300 K. 
Now, we analyze the control of the Kerr nonlinear coefficient via the intensity of 
the coupling field by plotting the Kerr nonlinear coefficient versus probe detuning p for 
DALAT UNIVERSITY JOURNAL OF SCIENCE [NATURAL SCIENCES AND TECHNOLOGY] 
51 
various values of the coupling Rabi frequency c = 0 (dash-dotted line), c = 50 MHz 
(dashed line), and c = 100 MHz (solid line), as shown in Figure 3(a). The variations of 
the Kerr nonlinear coefficient versus the Rabi frequency of the coupling field when c = 0, 
 p = 10 MHz (solid line), p = -10 MHz (dashed line), and T = 300 K are illustrated in 
Figure 3(b). From Figure 3(a) we can see a fundamental modification and great 
enhancement of the Kerr nonlinear coefficient inside the EIT window. This means that a 
normal dispersive curve appears on a line profile of the Kerr nonlinear coefficient 
accompanied by a pair of negative-positive values of n2 around the resonant frequency of 
the probe field p = 0. By increasing the coupling intensity, the amplitude of this 
dispersive curve is enhanced considerably. Figure 3(b) shows that the magnitude and sign 
of the Kerr nonlinear coefficient are changed by adjusting the coupling Rabi frequency. 
(a) 
(b) 
Figure 4. (a) The Kerr nonlinear coefficient as a function of probe detuning with 
different values of coupling detuning c = 0 (dash-dotted line), c = 15 MHz (dashed 
line), and c = -15 MHz (solid line); (b) The Kerr nonlinear coefficient as a function 
 of coupling detuning when p = 0 
Note: Other parameters are taken as c = 100 MHz and T = 300 K. 
In Figure 4, we analyze the control of the Kerr nonlinear coefficient according to the 
frequency of the coupling field when the coupling intensity is fixed at c = 100 MHz. 
Figure 4(a) shows the variations of the Kerr nonlinear coefficient with probe detuning p 
for different values of the coupling detuning c = 0 (dash-dotted line), c = -15 MHz 
(solid line), and c = 15 MHz (dashed line). We can see that a zero point for the Kerr 
nonlinear coefficient at the probe resonant frequency p = 0 in the case of c = 0 is 
transformed into a positive peak or negative peak when c = 15 MHz or c = -15 MHz, 
respectively. The change of the Kerr nonlinear coefficient with the coupling detuning 
when p = 0 and c = 100 MHz is presented in Figure 4(b). It shows that the variation of 
the Kerr nonlinear coefficient with the coupling detuning is similar to the variation of the 
Le Van Doai and Dinh Xuan Khoa 
52 
Kerr nonlinear coefficient with the probe detuning. That is, it also has a pair of negative-
positive peaks of the Kerr nonlinear coefficient around the resonant frequency of the 
coupling field c = 0. When the coupling frequency goes away from the atomic resonant 
frequency, the amplitude of the Kerr nonlinear coefficient decreases rapidly to zero. This 
is because the Kerr nonlinear coefficient is only enhanced in the EIT spectral domain 
when the condition of two-photon resonance is established ( p = c = 0). The sign of the 
nonlinear coefficient can also be changed by adjusting the coupling frequency to the short 
or long wavelength domain. 
Finally, we analyze the dependence of the Kerr nonlinear coefficient on 
temperature by plotting the Kerr nonlinear coefficient versus probe detuning p for 
various temperatures T = 100 K (solid line), T = 200 K (dashed line), and T = 300 K (dash-
dotted line), as illustrated in Figure 5(a). The variations of the Kerr nonlinear coefficient 
with temperature when c = 100 MHz, c = 0, p = 10 MHz (solid line), and p = -10 
MHz (dashed line) are shown in Figure 5(b). From the figure we can see that the profile 
of the nonlinear coefficient is greatly broadened and its amplitude is remarkably reduced 
when the temperature increases. 
(a) 
(b) 
Figure 5. (a) The Kerr nonlinear coefficient as a function of probe detuning for 
different temperatures T = 100 K (solid line), T = 200 K (dashed line), and T = 300 K 
(dash-dotted line); (b) The Kerr nonlinear coefficient as a function of temperature 
for different values of probe detuning p = -10 MHz (dashed line) and p = 10 MHz 
 (solid line) 
Note: Other parameters are taken as c = 0 and c = 100 MHz. 
4. CONCLUSION 
We have analyzed the enhancement and control of the self-Kerr nonlinear 
coefficient in a three-level V-type inhomogeneously broadened atomic medium by the 
analytical method. The study results have shown that the Kerr nonlinear coefficient is 
DALAT UNIVERSITY JOURNAL OF SCIENCE [NATURAL SCIENCES AND TECHNOLOGY] 
53 
enhanced considerably under the EIT condition. By adjusting the intensity or frequency 
of the coupling field, the magnitude and sign of the Kerr nonlinear coefficient are also 
changed significantly. The amplitude of the Kerr nonlinear coefficient decreases 
remarkably as temperature increases (i.e., the Doppler width increases). We note that the 
relaxation rate between excited states in the V-type scheme is much greater than that in 
the lambda-type scheme; therefore, the enhancement of the Kerr nonlinear coefficient 
occurs at a stronger coupling intensity. The analytical model can find potential 
applications in photonic devices and can explain the experimental observations of the 
Kerr nonlinear coefficient at different temperatures. 
ACKNOWLEDGMENTS 
The financial support from the Vietnamese National Foundation of Science and 
Technology Development (NAFOSTED) through the grant code 103.03-2017.332 is 
acknowledged. 
REFERENCES 
Anton, M. A.,  Calderon, O. G. (2002). Optical bistability using quantum interference 
in V-type atoms. Journal of Optics B: Quantum and Semiclassical Optics, 4, 91-98. 
Bai, Y., Guo, H., Han, D.,  Sun, H. (2005). Effects of spontaneously generated 
coherence on the group velocity in a V system. Physical Letters A, 340(1-4), 
342-346. 
Bai, Y., Guo, H., Sun, H., Han, D., Liu, C.,  Chen, X. (2004). Effects of spontaneously 
generated coherence on the conditions for exhibiting lasing without inversion in 
a V system. Physical Review A, 69, 1-5. 
Bai, Y., Liu, T.,  Yu, X. (2012). Giant Kerr nonlinearity in an open V-type system with 
spontaneously generated coherence. Optik, 124(7), 613-616. 
Bang, N. H., Doai, L.V.,  Khoa, D. X. (2019). Controllable optical properties of multiple 
electromagnetically induced transparency in gaseous atomic media. 
Communications in Physics, 29(1), 1-33. 
Bang, N. H., Khoa, D. X., Son, D. H.,  Doai, L. V. (2019). Effect of Doppler broadening 
on giant self-Kerr nonlinearity in a five-level ladder-type system. Journal of the 
Optical Society of America B, 36(11), 3151-3158. 
Boller, K. J., Imamoglu, A.,  Harris, S. E. (1991). Observation of electromagnetically 
induced transparency. Physical Review Letters, 66, 2593-2596. 
Boyd, R. W. (2008). Nonlinear optics. Academic Press. 
Doai, L. V. (2019). Giant cross-Kerr nonlinearity in a six-level inhomogeneously 
broadened atomic medium. Journal of Physics B: Atomic, Molecular and Optical 
Physics, 52, 1-9. 
Le Van Doai and Dinh Xuan Khoa 
54 
Doai, L. V., Khoa, D. X.,  Bang, N. H. (2015). EIT enhanced self-Kerr nonlinearity in 
the three-level lambda system under Doppler broadening. Physica Scripta, 90(4), 
1-6. 
Fleischhauer, M., Imamoglu, I.,  Marangos, J. P. (2005). Electromagnetically induced 
transparency: Optics in coherent media. Reviews of Modern Physics, 77, 633-673. 
Gao, H., Sun, H., Fan, S.,  Zhang, H. (2016). Phase control of Kerr nonlinearity in V-
type system with spontaneously generated coherence. Journal of Modern Optics, 
63(6), 598-604. 
Hamedi, H. R., Gharamaleki, A. H.,  Sahrai, M. (2016). Colossal Kerr nonlinearity 
based on electromagnetically induced transparency in a five-level double-ladder 
atomic system. Applied Optics, 55(22), 5892-5899. 
Hamedi, H. R.,  Juzeliunas, G. (2015). Phase-sensitive Kerr nonlinearity for closed-
loop quantum systems. Physical Review A, 91, 1-13. 
Han, D., Zeng, Y., Bai, Y., Chen, W., & Lu, H. (2007). Phase effects on group velocity 
propagation in a V-type system with spontaneously generated coherence. Journal 
of Modern Optics, 54, 493-500. 
Harris, S. E., Field, J. E.,  Imamoglu, A. (1990). Nonlinear optical processes using 
electromagnetically induced transparency. Physical Review Letters, 64, 1107-1110. 
Harris, S. E.,  Hau, L. V. (1995). Nonlinear optics at low light levels. Physical Review 
Letters, 82, 4611-4614. 
Joshi, A., Yang, W.,  Xiao, M. (2003). Effect of quantum interference on optical 
bistability in the three-level V-type atomic system. Physical Review A, 68, 1-4. 
Khoa, D. X., Doai, L. V., Son, D. H.,  Bang, N. H. (2014). Enhancement of self-Kerr 
nonlinearity via electromagnetically induced transparency in a five-level cascade 
system: An analytical approach. Journal of the Optical Society of America B, 
31(6), 1330-1334. 
Li, J. (2007). Coherent control of optical bistability in a microwave-driven V-type atomic 
system. Physica D: Nonlinear Phenomena, 228(2), 148-152. 
Li, Y.-q.,  Xiao, M. (1995a). Electromagnetically induced transparency in a three-level 
Λ-type system in rubidium atoms. Physical Review A, 51(4), 2703-2706. 
Li, Y.-q.,  Xiao, M. (1995b). Electromagnetically induced transparency in ladder-type 
inhomogeneously broadened media: Theory and experiment. Physical Review A, 
51(1), 576-584. 
Mousavi, S. M., Safari, L., Mahmoudi, M.,  Sahrai, M. (2010). Effect of quantum 
interference on the optical properties of a three-level V-type atomic system 
beyond the two-photon resonance condition. Journal of Physics B: Atomic, 
Molecular and Optical Physics, 43, 1-8. 
Sheng, J., Yang, X., Wu, H.,  Xiao, M. (2011). Modified self-Kerr-nonlinearity in a 
four-level N-type atomic system. Physical Review A, 84, 1-5. 
DALAT UNIVERSITY JOURNAL OF SCIENCE [NATURAL SCIENCES AND TECHNOLOGY] 
55 
Wang, H., Goorskey, D.,  Xiao, M. (2001). Enhanced Kerr nonlinearity via atomic 
coherence in a three-level atomic system. Physical Review Letters, 87(7), 1-4. 
Zhao, J., Wang, L., Xiao, L., Zhao, Y., Yin, W.,  Jia, S. (2002). Experimental 
measurement of absorption and dispersion in V-type cesium atom. Optics 
Communications, 206, 341-345.