An approach to solve the problem of data fusion for multi - target tracking using fuzzy logic

 Special Issue, No.66A, 5 - 2020 17 
)()()( kvkkv jtjt
J
j
t   (2) 
Where: 10 )]([)]([)(
  kbbkbk jt
J
j
jjtjt - is the probability that the thj 
“return” is originated from the tht track; 
 )}(/)]().(1.{[)(
2/)2()(0 kDkFkDktS
Mkjb ; 
)}().(1)]().[5.0exp{()( kjtvktS
Tkjtvkjtb
)(kD - is the probability of target detection at the thk updated period; )(kD - 
is the probability of a target return falling within the validation gate; )(ktS - is the 
innovation covariance and M is the dimension of the measurement vector. 
The estimated error covariance matrix, associated with maneuvering state 
)(ˆ kktx , is given by the estimation of filter covariance: 
 )(
~
)()](1[)]1([ˆ)()(ˆ 00 kPkkPkkkPkkkP t
c
ttttt  (3) 
Where: 
 1. )]([ˆ)]()([)( kkPkHkKIkkP ttt
c
t (4) 
 2. ( ) ( ) { ( ) ( ) [ ( )] ( ) [ ( )] } [ ( )]
J
T T T
t t jt jt jt t t t
j
P k K k k v k v k v k v k K k  (5) 
 3. )()]1([)]1()1[(ˆ)1()]1([ˆ ktQ
TktFkktPktFkktP (6) 
 4. )(
1)]([)]1([ˆ)( ktS
TktHkktPktK
 (7) 
)(0 kt - is the a priori probability that all measurements in the validation gate of 
tht track are false; )(ktF - is the transition matrix in the state equation; )(ktH - is 
the linearization measurement matrix for tht target; )(ktK - is the Kalman filter 
gain; )(ktQ - is the the process noise covariance matrix. 
Note that, in the calculation of ( )jt k , the PDFA assumes that all the tracks are 
isolated and does not take into account the possibility that some observations in the 
gate may come from other targets [9]. 
2.2. Joint probabilistic data fusion 
According to [11], for the JPDF, the probability of tht track being associated 
with thj observation - “point”, is the sum of the probabilities of all joint events, 
)(k , in which tht track is associated with thj observation - “point”, which 
can be expressed as: 
( )
( ) P[ ( ) ] [ ( )]Kjt jt
k
k k Z k 

   (8) 
Electronics & Automation 
D. Q. Hieu, , V. C. Thanh, “An approach to solve the problem  using fuzzy logic.” 18 
Where, [ ( )]jt k  is a binary variable indicating whether tht track is 
associated with thj fusion in the event )(k . The probability of the event ( )k
given KZ , the set of all the observations received up to the current scan k , is 
given by [3] (that to mean: 1( ) ( ), , ( )jZ k z k z k - set of measurement points up 
to the time k , and (1), , ( )KZ Z Z k . 
(1 )
1 1
1 !
[ ( ) | ( )] { [ ( )]} [ ( )] [1 ( )]
[ ( )]
t
j t t
MJ
jt t tn
j m
n
k Z k N k D k D k
C V k
   
    
(9) 
Where, C - is a normalization constant; )(kV - is the gate volume, n - is the 
number of observations determined to be clutter in )(k and [ ( )]jtN k - is the 
normal probability density function with zero-mean and a covariance matrix 
equaling to ( )jt k . Define two quantities, j and t , such that j is equal to one if 
the j th observation is assigned to a track in the event ( )k and zero otherwise, 
and t is equal to one if the tht track has been assigned an observation and zero 
otherwise. Assuming a Poission density function for clutter points, the probability 
of the event ( )k has to take into account the history of observations up until 
updated period )]([ kZk . The Kalman filter is updated using the same set of 
equations as in the PDFA. 
2.3. Discussion 
1. The JPDFA approach provides an optimal data fusion solution in the 
Bayesian framework. However, the number of possible hypothesis associating 
different returns to targets in the JPDF increases rapidly with the number of targets 
and the presence of clutter. Consequently, this approach requires a large amount 
for processor time calculating the joint probabilities even for a small number of 
targets in the high level of the clutter [5, 7, 8]. 
2. To solve this problem, an alternative method of JPDA should be investigated. 
Possible approaches might be based on neural network and fuzzy logic. 
3. SOLVING THE PROBLEM OF DATA FUSION FOR MULTI-TARGET 
TRACKING USING FUZZY LOGIC 
Fundamentally, the conventional tracking techniques are too restrictive to deal 
with the complexity of tracking problem. There is a very sharp demarcation line 
between target and non-target at the intersecting gates [7, 8, 10]. This type of target 
classification clearly does not reflect well. By incorporating human-like reasoning 
into the tracking problem, results comparable to the JPDA can be achieved. The 
structural schematic of the fuzzy tracking system is showed in fig.1. It consists of 
the following function blocks. 
+ KF: the standard suboptimal Kalman filter that gives values of state estimates 
and their covariances. Inputs are the state estimate vector )(ˆ kx , its covariance 
matrix )(ˆ kP , and the measurements vector z . 
Research 
Journal of Military Science and Technology, Special Issue, No.66A, 5 - 2020 19 
+ Fuzzy data fusion (FDF) was used to evaluate the association degree between the 
return and the actual of interest (not clutter or other targets). Inputs are the 
measurement innovation, which is based on the availability of objective and/or 
heuristic. Here, we will use the FDA approach instead of the JPDAF approach. 
Namely, the state estimate is then adjusted according to 
.
( ) ( , , )
fus
jt k FDF A   (10) 
Kalman 
Filter
Start 
Setup
 measurement set 
FusionDataFuzzy
)(. kFuzjt
)(ˆ kx jt
)(ˆ)(. kxk jt
Fuz
jt
j
  
1 kk
)(ˆ kxt
)(kP
Figure 1. The structure schematic of the fuzzy tracking system. 
The (*)FDF - is fuzzy function, which is used to evaluate the association degree 
.( )fus
jt
k at the thk updated period based on the set of membership functions A 
and the set of some proposition [10, 14]. Thus, the FDA keep the main idea of 
the JPDA, but can incorporate additional information or some of heuristic rules. 
Using fuzzy logic methodology, the rules in the FDF rule base are evaluated. The 
FDA rules to determine the degree of fusion are the form in: 
......
)(
.~~
:3
)(
.~~
:2
)(
.~~
:1
ThenIf
MLk
fus
jtThenNSisRZandNLisRZIfR
VLk
fus
jtThenNMisRZandNLisRZIfR
VLk
fus
jtThenNLisRZandNLisRZIfR



(11) 
For example, in the case of using the distance attribute (angle and distance), 
then the fuzzy variable, FDF, has 49 “ THENIF ” rules provided in table 1. 
Table 1. FDF Rule Base. 
Fusion Degree Range Error 
NL NM NS Z PS PM PL 
A
zi
m
u
th
E
rr
o
r 
NL VL VL ML M ML VL VL 
NM VL ML ML M ML ML VL 
NS ML ML M MH M ML ML 
Z M M MH VH MH M M 
Electronics & Automation 
D. Q. Hieu, , V. C. Thanh, “An approach to solve the problem  using fuzzy logic.” 20 
PS ML ML M MH M ML ML 
PM VL ML ML M ML ML VL 
PL VL VL ML M ML VL VL 
In this table, the fuzzy terminology of Input variables are given by (12). And 
the fuzzy term set of output Output variables were given by (13): 
NL denote Negative Large
NM denote Negative Medium
NS denote Negative Small
Z denote Zero
PS denote Positive Small
PM denote Positive Medium
PL denote Positive Large
(12) 
HighVerydenoteVH
HighMediumdenoteMH
MediumdenoteM
LowMediumdenoteML
LowVerydenoteVL
(13) 
4. SIMULATION RESULTS 
In this section, we will present the simulation results of applying fuzzy data 
fusion for multi-target tracking. The initialization process of measurement set and 
data is presented in [1, 5]. The radar sensors provide range and azimuth 
measurements to the tracking algorithm, which estimates the position and velocity 
of the target in the horizontal plane. The setup data of measurement sets for 
simulation is presented in [5]. The simulation with minimum separation distance 
flight scenario is chosen from the benchmark problem for maneuvering targets. 
The measurement noise is zero-mean Gaussian with a standard deviation of 120m 
for range and 15 milidegree for azimuth and elevation angles. 
4.1. Configuration problem 
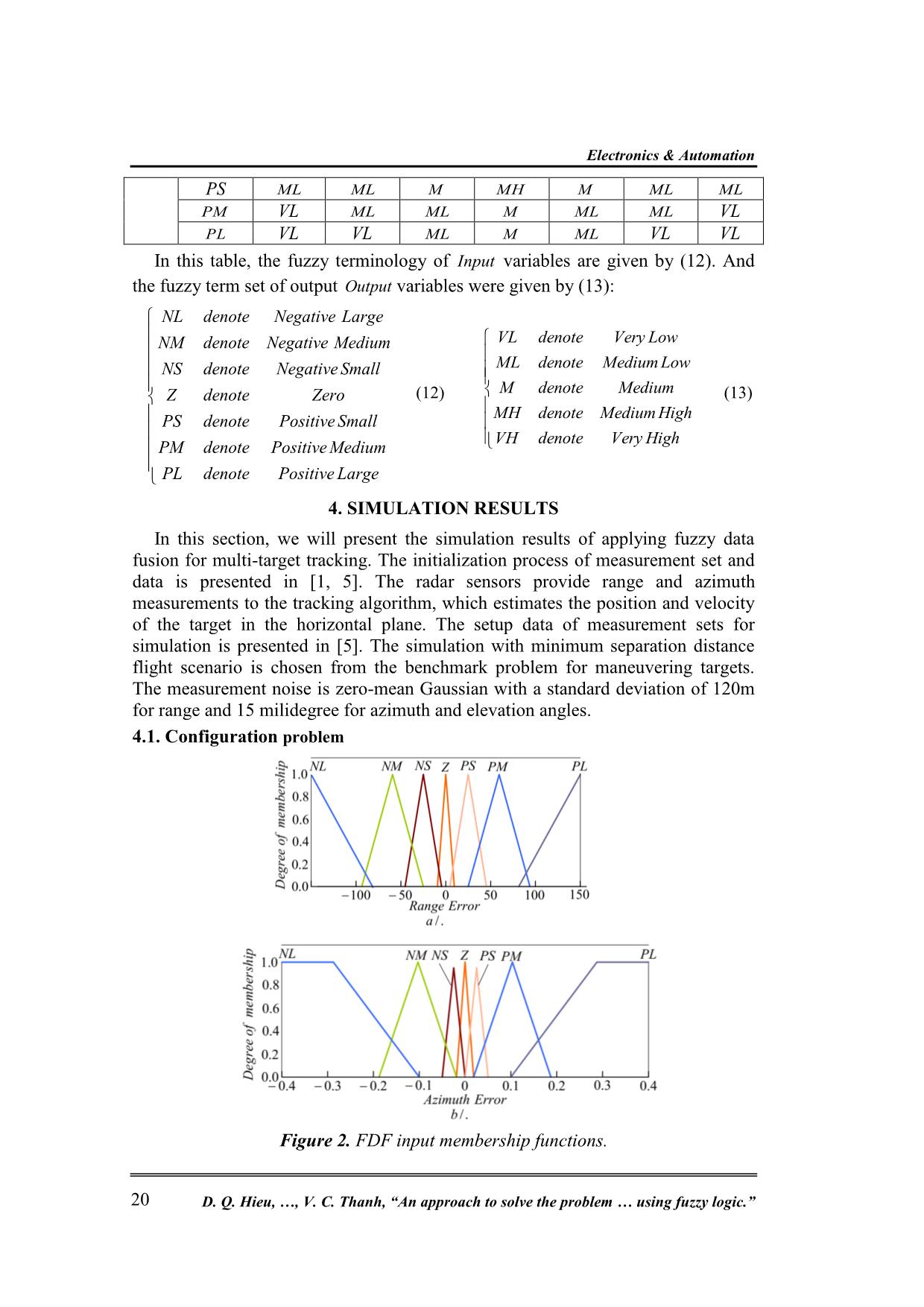
Figure 2. FDF input membership functions. 
Research 
Journal of Military Science and Technology, Special Issue, No.66A, 5 - 2020 21 
The fuzzy data fusion is presented to demonstrate the feasibility of using fuzzy 
logic for maneuver detection and data association in cluttered environment. 
For the FDF configurations, the sets of membership functions which fuzzify 
these crisp inputs, defined over appropriate universe of discourse are shown in 
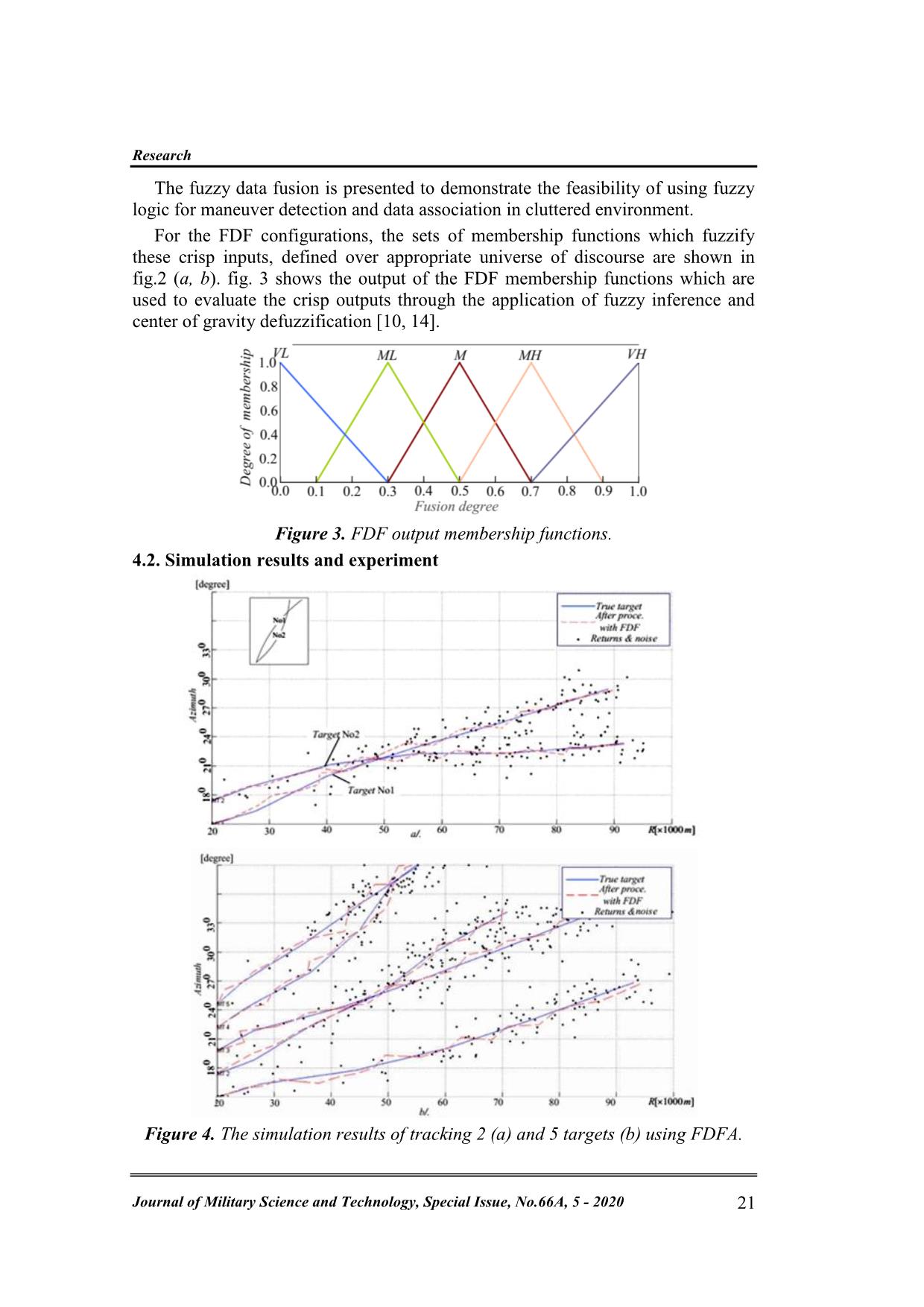
fig.2 (a, b). fig. 3 shows the output of the FDF membership functions which are 
used to evaluate the crisp outputs through the application of fuzzy inference and 
center of gravity defuzzification [10, 14]. 
Figure 3. FDF output membership functions. 
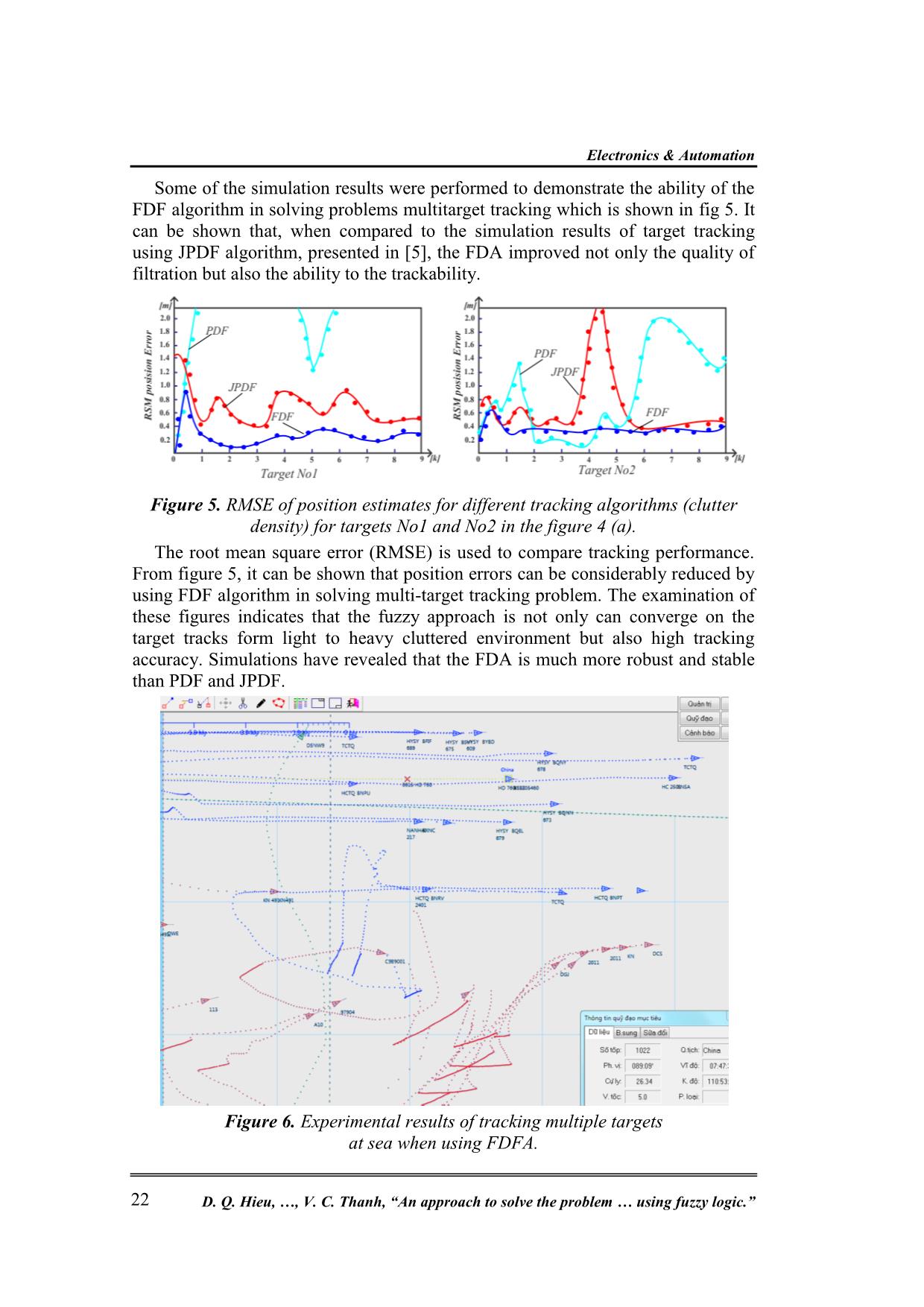
4.2. Simulation results and experiment 
Figure 4. The simulation results of tracking 2 (a) and 5 targets (b) using FDFA. 
Electronics & Automation 
D. Q. Hieu, , V. C. Thanh, “An approach to solve the problem  using fuzzy logic.” 22 
Some of the simulation results were performed to demonstrate the ability of the 
FDF algorithm in solving problems multitarget tracking which is shown in fig 5. It 
can be shown that, when compared to the simulation results of target tracking 
using JPDF algorithm, presented in [5], the FDA improved not only the quality of 
filtration but also the ability to the trackability. 
Figure 5. RMSE of position estimates for different tracking algorithms (clutter 
density) for targets No1 and No2 in the figure 4 (a). 
The root mean square error (RMSE) is used to compare tracking performance. 
From figure 5, it can be shown that position errors can be considerably reduced by 
using FDF algorithm in solving multi-target tracking problem. The examination of 
these figures indicates that the fuzzy approach is not only can converge on the 
target tracks form light to heavy cluttered environment but also high tracking 
accuracy. Simulations have revealed that the FDA is much more robust and stable 
than PDF and JPDF. 
Figure 6. Experimental results of tracking multiple targets 
at sea when using FDFA. 
Research 
Journal of Military Science and Technology, Special Issue, No.66A, 5 - 2020 23 
The FDA has been partially experimented in the Integration and Management 
System of Coastal Surveillance in the Navy Headquarter, in order to improve the 
performance of multiple-radar target data processing and ensuring the near real-
time of the observation. It was proven to be effective in reducing computing load 
and simplify the computation structure. The novel method gives an explicit 
indication of the possibility to incorporate useful knowledge into tracking problem. 
A mid-range workstation, on which the FDF algorithm has been performed, can 
fully handle the correlation processing hundreds of multi-sensor target data in the 
same region, which transmitted from 4 to 5 medium range coastal surveillance 
radar stations. On the command and control stations located in the headquarter, the 
combined sea target data was displayed on top of the digital map layers for the 
operator (fig 6). 
5. CONCLUSION 
In this paper, we have presented a set of fuzzy-based methods that can be 
applied in combination with the conventional Kalman filter for multi-target 
tracking in a cluttered environment. The given simulation examples show that the 
proposed approach effectively reduces the tracking error due to maneuvering and 
cluttered effects. The FDF approach was based on 49 heuristics hypotheses. These 
heuristics hypotheses are implemented to estimate the degree of association to 
which each measurement within the gate of tracking filter belongs to the true 
measurement fuzzy set. This algorithm has been partially experimented. Is was 
shown to be effective in reducing computing capacity and had a simple structure. 
REFERENCES 
[1]. Bao. N.F, Huy. P. N. “About some data association algorithms in radar processing 
problem” MS&TR Journal No: 19, Vol.6 2012. 
[2]. Bar-Shalom Y. “Multitarget–multisensor Tracking: Advanced applications”, Vol. II. 
Norwood, MA: Artech House, 1992 
[3]. Bar-Shalom Y (1995). “Multitarget-Multisensor Tracking: Principles and 
Techniques”, Norwood, MA: Artech House, 1995. 
[4]. David. L. “Multi-Sensor Multi-Target Data Fusion Tracking and Identification 
Techniques for Guidance and Control Applications”, North Atlantic Treaty 
Organization 1996. 
[5]. Huy. P. N. “An application of Hopfield network to solve radar data association 
problem”, Ph.D Thesis. Military Science and Technology Institute Hanoi, Vietnam, 
2015 
[6]. Farina A, Stunder F. A (1993). “Radar Data Processing”,Vol II,RSP, NY, 1993 
[7]. Kashyap. S. K (2008). “Fuzzy Logic Applications in Filtering and Fusion for Target 
Tracking”, DSJ Vol.85, No.1, Jan 2008 pp 120-135J. 
[8]. Krithika. S. “Radar Target Classification Using Fuzzy Logic”, IJFTET Vo 13 No 1 - 
May 2016. 
[9]. Omar. R, “Multiple Sensor Fusion for Detection, Classification and Tracking of 
Moving Objects in Driving Environments”, HAL Universite de Grenoble, 2014. 
[10]. Белов. С. Г (2017), “Использование нечёткой логики при отождествления 
воздушных РЛ обьектов”, Журнал Радиоэлектроники, ISSN 1684-1719M. 
[11]. Фарина.A, Cтудер.Ф, “Цифровая Обработка радиолокации информации, 
Electronics & Automation 
D. Q. Hieu, , V. C. Thanh, “An approach to solve the problem  using fuzzy logic.” 24 
Сопровождение Целей” , Изд. Радио и Связъ , Москва, 1993. 
[12]. Панасюк. Ю, “Обработка информации в радиотехнических системах”, Изд. 
ФГБОУ ВО «ТГТУ» 2016. 
[13]. А. Хижняк, “Разработка имитационной модели кластеризации воздушных 
объектов при решении задачи третичной обработк РЛИ на основе нечётких 
множеств”, ИММОД 2009. 
[14]. Чернов. В.Г, “Основы теории нечётких множеств”, Изд. ВГУ 2010 – 96 стр. 
[15]. Report on experimental results of science and technology projects NTD Navy 
Headquarter, Hai Phong, VietNam 2018. 
TÓM TẮT 
MỘT CÁCH TIẾP CẬN GIẢI QUYẾT VẤN ĐỀ HỢP NHẤT DỮ LIỆU 
TRONG BÁM SÁT ĐA MỤC TIÊU SỬ DỤNG LÔ GÍC MỜ 
Bài báo trình bày về một thuật toán hợp nhất (liên kết) dữ liệu đa mục tiêu 
được gọi là thuật toán hợp nhất dữ liệu mờ (Fuzzy Data Fusion Algorithm - 
FDFA) dùng để lọc,bám sát quỹ đạo đa mục tiêu ra đa. Cách tiếp cận này 
được xây dựng dựa trên cơ sở sử dụng công cụ lọc Kalman và hợp nhất dữ 
liệu mờ (Fuzzy Data Fusion - FDF. Các kết quả mô phỏng cho các điều kiện 
nhiễu cho thấy hiệu suất của thuật toán được đề xuất tốt hơn so hai thuật 
toán hợp nhất dữ liệu theo xác xuất (Probabilistic Data Fusion - PDF) và 
hợp nhất dữ liệu theo xác xuất liên kết (Joint Probabilistic Data Fusion - 
JPDF), như đã được trình bày trong [2-4, 6]. 
Từ khóa: Hợp nhất dữ liệu (liên kết dữ liệu); Bám sát đa mục tiêu; Lô-gích mờ. 
Received 08th January, 2020 
Revised 17h March, 2020 
Published 06th May, 2020 
Author affiliations: 
 1 Institute of System Integration, Military Technical Academy; 
 2 Radar Institute, Academy of Military Science and Technology. 
 *Email: hieudq@mta.edu.vn.