A unified port - hamiltonian approach for modelling and stabilizing control of engineering systems

 (32). Let M(x) be the square matrix given by (
– 
) it follows that 
 ( ) ( ) (
). It can easily be checked that the separability condition (2) is met for f(x) 
above where H(x) is of the quadratic form (7) with Rdi given by (29). Using the fact that any 
square matrix can uniquely be written as sum of a symmetric and a skew-symmetric matrix 
thanks to the Toeplitz decomposition of linear algebra, one may write ( ) 
 ( ) ( ) 
 and 
 ( ) 
 ( ) ( ) 
 that lead to Eqs. (30) and (31), respectively. Finally, the damping matrix 
R(x) (31) is symmetric positive definite because all the principal minors of R(x) are (strictly) 
positive due to the fact that k1 = k2. The latter completes the proof. 
3.2. Case study 2: A continuous biochemical fermenter system 
We consider next the dynamic model of a second order continuous biochemical fermenter 
described by the equations (see Section 4 in [3]) 
 {
 ( ) 
 ( )
( )
 (34) 
where: 
 cx and cs denote the cell and substrate concentrations, respectively; 
 The term µ = µ(cs) denotes the specific cell growth rate; 
 q is the volumetric inflow rate of the reactor and is equal to the outflow rate; 
 V is the total reactor volume and is assumed to be constant; 
 Sf is the feed of substrate entering the reactor; 
 Y is the biomass/substrate yield coefficient. Let us state the following proposition. 
Let us state the following proposition. 
A unified port-hamiltonian approach for modelling and stabilizing control of engineering systems 
103 
Proposition 2. The system dynamics (34) are a quadratic pseudo PH representation (4) where 
 ( )
 ( )
 and the Hamiltonian storage function is of the form (7) with 
(
) (35) 
and 
 ( ) (
 ( )
 ⁄
 ( )
 ⁄ 
) (36) 
 ( ) (
 ( )
 ( )
 ⁄
 ( )
 ⁄ 
) (37) 
 ( ) (
) 
 (38) 
 ( ) 
 (39) 
Proof. Equations in (34) are rewritten as 
 (
) (
 ( ) 
 ( )
)
⏟ 
 ( )
(
) (
)
 (40) 
From this, the proof immediately follows by using the same arguments as done in the previous 
case study. Note that the symmetric matrix R(x) (37) is indefinite (i.e. neither positive definite 
nor negative definite). 
3.3. Further discussions 
Two of the main advantages of the quadratic (pseudo) PH representation are summarized as 
follows, (i) it circumvents the passivation design of the dynamics by input coordinate 
transformations [14] and (ii) it enables the control design via tracking-error approach with 
specific control benefits compared to the interconnection and damping assignment passivity-
based control (IDA-PBC) approach [10, 12], that is, no need to solve matching equations that are 
expressed by partial differential equations. 
In the quadratic (pseudo) PH framework, the key idea of the tracking-error passivity-based 
control approach consists in guaranteeing that the system trajectory x globally exponentially 
tracks some reference trajectory xd when time goes to infinity while xd is of the form 
 [ ( ) ( )]
 ( )
 ( )
 ( )
 ( ) (41) 
where the damping injection RI(x) is a symmetric positive definite matrix to be appropriately 
chosen such that
4
 ( ) ( ) (42) 
and ( ) 
 Rdie with e = x – xd the error state vector. At the control design stage, only m 
components of the reference trajectory xd are chosen in such a way that their time evolutions 
converge globally asymptotically or exponentially to the corresponding m-values of the desired 
4
We refer the reader to [21, 22] for a complete proof. 
Ngoc-Ha Hoang, Phuong-Quyen Le, Chi-Thuan Nguyen 
104 
constant set-point x
*
, that is, 
 ( 
∗ ) i = 1, . . . , m, provided that the corresponding 
m m submatrix obtained from g(x) is full rank. 
As a matter of illustration, we reconsider the Case study 2 (Subsection 3.2) where the 
specific cell growth rate µ(cs) is assumed given by the Monod-kinetics with an additional 
substrate overshoot term [3] 
 ( ) 
 (43) 
where the scalars µmax, d1 and d2 are positive. The continuous fermenter system exhibits the 
combined input-output multiplicities behaviour [3, 16] which is very challenging but interesting 
for the stabilizing control design. A three-step design procedure is provided below with the 
tracking-error passivity-based control approach. 
Step 1 (the damping injection): From the damping matrix R(x) (37) and the stabilization 
condition (42), the damping injection element RI(x) can be chosen as 
 ( ) (
 ( ) 
 ( )
 ( )
) (44) 
where δ1 and δ2 are positive. 
Step 2 (the reference trajectory): From Proposition 2 and Eqs. (41) and (44), the reference 
trajectory is given by: 
 ( ) ( ( ) )( ) 
 ( )
( ) (45) 
 ( )
 ( )
( ) ( ) ( ) (46) 
Step 3 (the control design): First, the dynamics of xd,1 is chosen to be assigned, that is, 
 ( 
∗ ) where the scalar K is positive while 
∗ is the first component of the desired set-
point ∗ ( 
∗ 
∗) . The state feedback law is then derived from (45) as 
( ( 
∗ ) ( ) ( ( ) )( ) 
 ( )
( )) (47) 
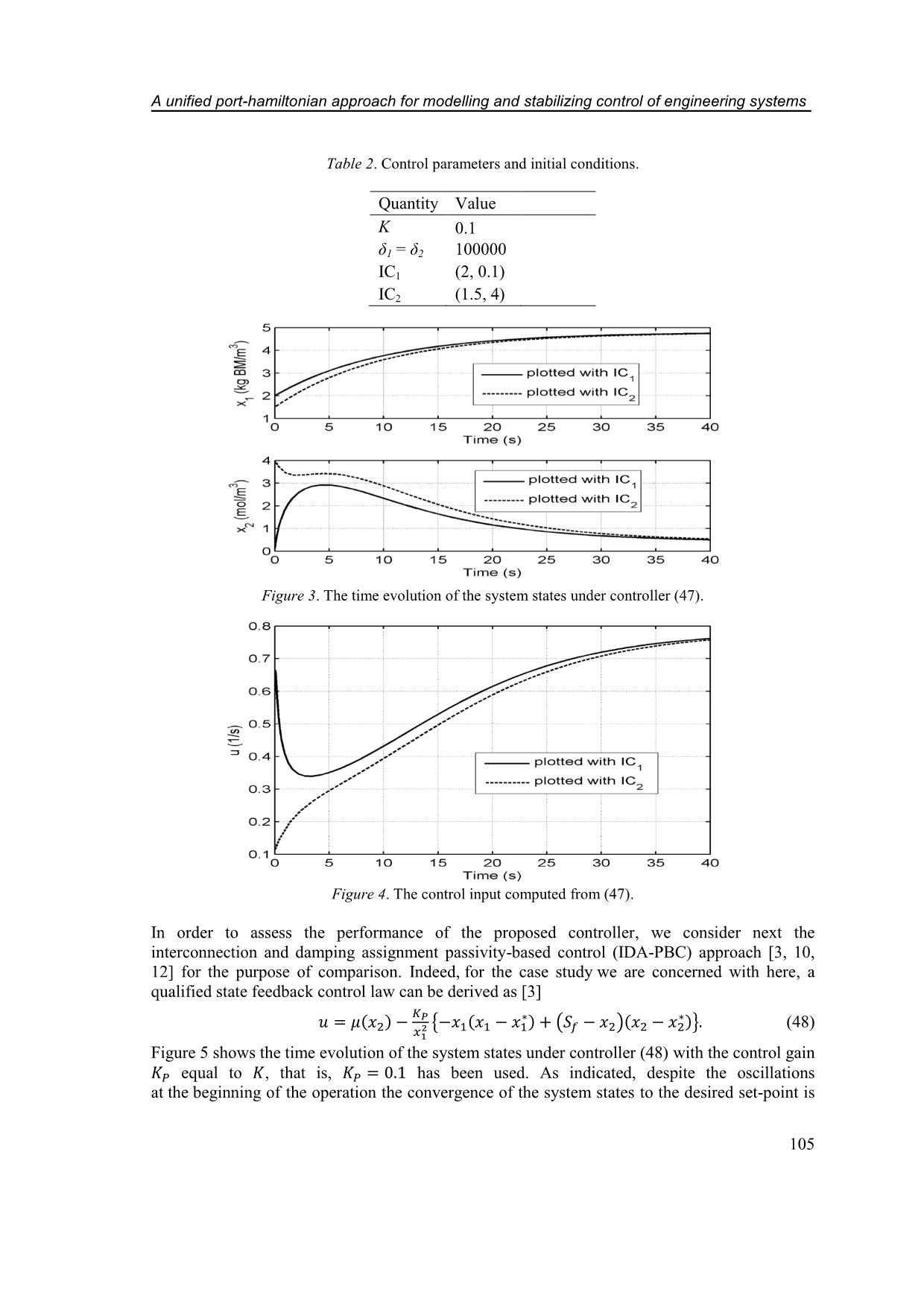
The simulation parameters can be found in Tables 1 and 2. Figure 3 shows that the 
convergence of the system state x to the desired set-point ∗ is guaranteed with the 
corresponding control input u (see Fig. 4). 
Table 1. Simulation parameters of the fermenter model [3]. 
Quantity Value Unit 
µmax 1 1/s 
d1 0.03 mol/m
3
Sf 10 mol/m
3
 s 
Y 0.5 mol/kg BM 
d2 0.5 m
3
/mol 
x* (4.80, 0.40) 
A unified port-hamiltonian approach for modelling and stabilizing control of engineering systems 
105 
Table 2. Control parameters and initial conditions. 
Quantity Value 
K 0.1 
δ1 = δ2 100000 
IC1 (2, 0.1) 
IC2 (1.5, 4) 
Figure 3. The time evolution of the system states under controller (47). 
Figure 4. The control input computed from (47). 
In order to assess the performance of the proposed controller, we consider next the 
interconnection and damping assignment passivity-based control (IDA-PBC) approach [3, 10, 
12] for the purpose of comparison. Indeed, for the case study we are concerned with here, a 
qualified state feedback control law can be derived as [3] 
 ( ) 
 { ( 
∗) ( )( 
∗)} (48) 
Figure 5 shows the time evolution of the system states under controller (48) with the control gain 
 equal to , that is, has been used. As indicated, despite the oscillations 
at the beginning of the operation the convergence of the system states to the desired set-point is 
Ngoc-Ha Hoang, Phuong-Quyen Le, Chi-Thuan Nguyen 
106 
in about 20 seconds, i.e. the settling time is two times faster than the one with controller (47) 
(see Figure 3). Nevertheless, if no input constraint (i.e. the input saturation or ( ) ) is 
imposed, this feature could be paid to the admissibility of the control input due to its negative 
value which is physically inacceptable as seen in Figure 6. In other words, the fermenter system 
under controller (47) may be operated with better performance (i.e. avoiding a very fast settling 
time provided by a larger domain of validity for operating conditions and initial conditions). 
Figure 5. The time evolution of the system states under controller (48). 
Figure 6. The control input computed from (48). 
4. CONCLUSION 
In this work, an introductory survey of the port Hamiltonian-based modelling of linear 
electrical and mechanical systems is given. This modelling framework can be adapted for 
nonlinear chemical and biological systems leading to a unified quadratic (pseudo) PH 
A unified port-hamiltonian approach for modelling and stabilizing control of engineering systems 
107 
representation. The resulting presentation enables the tracking-error passivity-based control 
approach with specific control benefits. It remains now to extend the proposed approach to large 
dimensional engineering systems. 
Acknowledgments. This research is funded by Vietnam National Foundation for Science and Technology 
Development (NAFOSTED) under grant number 103.99-2019.385. 
Author contributions: Author 1: Conceptualization, Formal analysis, Funding acquisition, Methodology, 
Resources, Software, Writing-original draft, Writing-review & editing. Author 2: Writing-original draft. 
Author 3: Writing-original draft. 
Conflict statement: The authors declare that they have no known competing financial interests or personal 
relationships that could have appeared to influence the work reported in this paper. 
REFERENCES 
1. Khalil H. K. - Nonlinear systems, Prentice Hall, Upper Saddle River, 3rd edition, 2002. 
2. Ortega R., Loría A., Nicklasson P. J., Sira – Ramírez H. - Passivity-based control of 
Euler-Lagrange systems Mechanical, electrical and electromechanical applications, 
Springer London, 1st edition, 1998. 
3. Dörfler F., Johnsen J. K., Allgöwer F. - Introduction to interconnection and damping 
assignment passivity-based control in process engineering, Journal of Process Control 
19 (9) (2009) 1413-1426. https://doi.org/10.1016/j.jprocont.2009.07.015. 
4. Favache A., Dochain D. - Power-shaping control of reaction systems: The CSTR case, 
Automatica 46 (11) (2010) 1877-1883. https://doi.org/10.1016/j.automatica.2010.07.011. 
5. Ramírez H., Maschke B., Sbarbaro D. - Irreversible port-Hamiltonian systems: A general 
formulation of irreversible processes with application to the CSTR, Chemical Engineering 
Science 89 (2013) 223-234. https://doi.org/10.1016/j.ces.2012.12.002. 
6. Couenne F., Jallut C., Maschke B., Breedveld P., Tayakout M. - Bond graph modelling 
for chemical reactors, Mathematical and Computer Modelling of Dynamical Systems 12 
(2-3) (2006) 159-174. https://doi.org/10.1080/13873950500068823. 
7. Eberard D., Maschke B., Van der Schaft A. - An extension of Hamiltonian systems to the 
thermodynamic phase space: Towards a geometry of nonreversible processes, Reports on 
Mathematical Physics 60 (2) (2007) 175-198. 
https://doi.org/10.1016/S0034-4877(07)00024-9. 
8. [8] Maschke B., Ortega R., Van der Schaft A. - Energy-based Lyapunov functions for 
forced Hamiltonian systems with dissipation, IEEE Transactions on Automatic Control 
45(8) (2000) 1498–1502, 2000. https://doi.org/10.1109/9.871758. 
9. Van der Schaft A. - Port-controlled Hamiltonian systems: Towards a theory for control 
and design of nonlinear physical systems, SICE Journal 39 (2) (2000) 91-98. 
https://doi.org/10.11499/sicejl1962.39.91. 
10. Ortega R., Van der Schaft A., Maschke B., Escobar G. - Interconnection and damping 
assignment passivity-based control of port-controlled Hamiltonian systems, Automatica 
38 (4) (2002) 585-596. https://doi.org/10.1016/S0005-1098(01)00278-3. 
Ngoc-Ha Hoang, Phuong-Quyen Le, Chi-Thuan Nguyen 
108 
11. Ortega R., Van der Schaft A., Castanos F., Astolfi A. - Control by interconnection and 
standard passivity-based control of port-Hamiltonian systems, IEEE Transactions on 
Automatic Control 53 (11) (2008) 2527-2542. 
https://doi.org/10.1109/TAC.2008.2006930. 
12. Wu D., Ortega R., Duan G. - On universal stabilization property of interconnection and 
damping assignment control, Automatica 119 (2020) 109087. 
https://doi.org/10.1016/j.automatica.2020.109087. 
13. Borja P., Ortega R., Scherpen J. M. A. - New results on stabilization of port-Hamiltonian 
systems via PID passivity-based control, IEEE Transactions on Automatic Control, in 
press, 2020. https://doi.org/10.1109/TAC.2020.2986731. 
14. Fujimoto K., Sakurama K., Sugie T. - Trajectory tracking control of port-controlled 
Hamiltonian systems via generalized canonical transformations, Automatica 39 (12) 
(2003) 2059-2069. https://doi.org/10.1016/j.automatica.2003.07.005. 
15. Monshizadeh N., Monshizadeh P., Ortega R., Van der Schaft A. - Conditions on shifted 
passivity of port-Hamiltonian systems, Systems & Control Letters 123 (2019) 55-61. 
https://doi.org/10.1016/j.sysconle.2018.10.010. 
16. Chidambaram M., Reddy G. P. - Nonlinear control of systems with input and output 
multiplicities, Computers & Chemical Engineering 20 (3) (1996) 295-299. 
https://doi.org/10.1016/0098-1354(95)00019-4. 
17. Guay M., Hudon N. - Stabilization of nonlinear systems via potential-based realization, 
IEEE Transactions on Automatic Control 61 (4) (2016) 1075-1080. 
https://doi.org/10.1109/TAC.2015.2455671. 
18. Favache A., Dochain D., Winkin J. J. - Power-shaping control: Writing the system 
dynamics into the Brayton-Moser form, Systems & Control Letters 60 (8) (2011) 618-624. 
https://doi.org/10.1016/j.sysconle.2011.04.021. 
19. Hoang N. H., Dochain D., Couenne F., Le Gorrec Y. - Dissipative pseudo-Hamiltonian 
realization of chemical systems using irreversible thermodynamics, Mathematical and 
Computer Modelling of Dynamical Systems 23 (2) (2017) 135-155. 
https://doi.org/10.1080/13873954.2016.1237973. 
20. Van der Schaft A. - L2-gain and passivity techniques in nonlinear control, Springer, 3rd 
edition, 2017. 
21. Nguyen T. S., Hoang N. H., Hussain M. A. - Feedback passivation plus tracking-error-
based multivariable control for a class of free-radical polymerization reactors, 
International Journal of Control 92 (9) (2019) 1970-1984. 
https://doi.org/10.1080/00207179.2017.1423393. 
22. Nguyen T. S., Hoang N. H., Hussain M. A., Tan C. K. - Tracking-error control via the 
relaxing port-Hamiltonian formulation: Application to level control and batch 
polymerization reactor, Journal of Process Control 80 (2019) 152-166. 
https://doi.org/10.1016/j.jprocont.2019.05.014. 
23. Batlle C. - Passive control theory I and II, The 2nd EURON/GEOPLEX Summer School 
on Modeling and Control of Complex Dynamical Systems, July 18-22, 2005, Bertinoro, 
Italy. 
A unified port-hamiltonian approach for modelling and stabilizing control of engineering systems 
109 
24. Mayergoyz I. D., Lawson W. - Basic electric circuit theory: A one-semester text, 
Academic Press, 1st edition, 2012. ISBN: 9780124808652. 
25. McCall M. W. - Classical mechanics: From Newton to Einstein - A modern introduction, 
Wiley, 2nd edition, 2010. ISBN: 9780470715741. 
26. Niemiec M. P., Kravaris C. - Nonlinear model-state feedback control for nonminimum-
phase processes, Automatica 39 (7) (2003) 1295-1302. https://doi.org/10.1016/S0005-
1098(03)00103-1. 
27. Antonelli R., Astolfi A. - Continuous stirred tank reactors: easy to stabilise? Automatica 
39 (10) (2003) 1817-1827. https://doi.org/10.1016/S0005-1098(03)00177-8. 
28. Ramírez H., Sbarbaro D., Ortega R. - On the control of non-linear processes: An IDA-
PBC approach, Journal of Process Control 19 (3) (2009) 405-414. 
 https://doi.org/10.1016/j.jprocont.2008.06.018. 
29. Nguyen T. S., Hoang N. H., Hussain M. A. - Tracking error plus damping injection 
control of non-minimum phase processes, IFAC-PapersOnLine 51 (18) (2018) 643-648. 
https://doi.org/10.1016/j.ifacol.2018.09.351. 
30. Farschman C. A., Viswanath K. P., Ydstie B. E. - Process systems and inventory control, 
AIChE Journal 44 (8) (1998) 1841-1857. https://doi.org/10.1002/aic.690440814.