A general model of fractional frequency reuse: Modelling and performance analysis

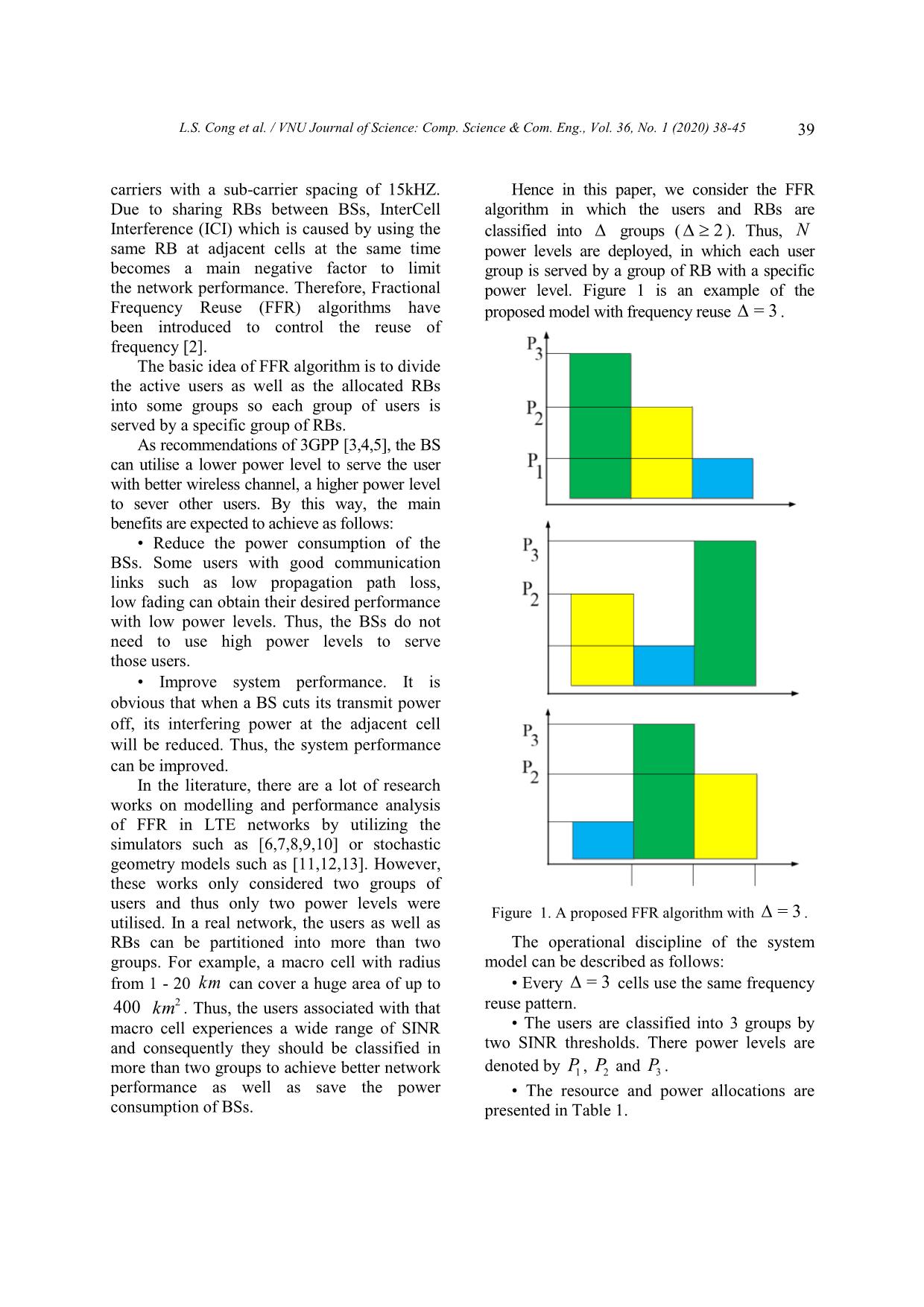
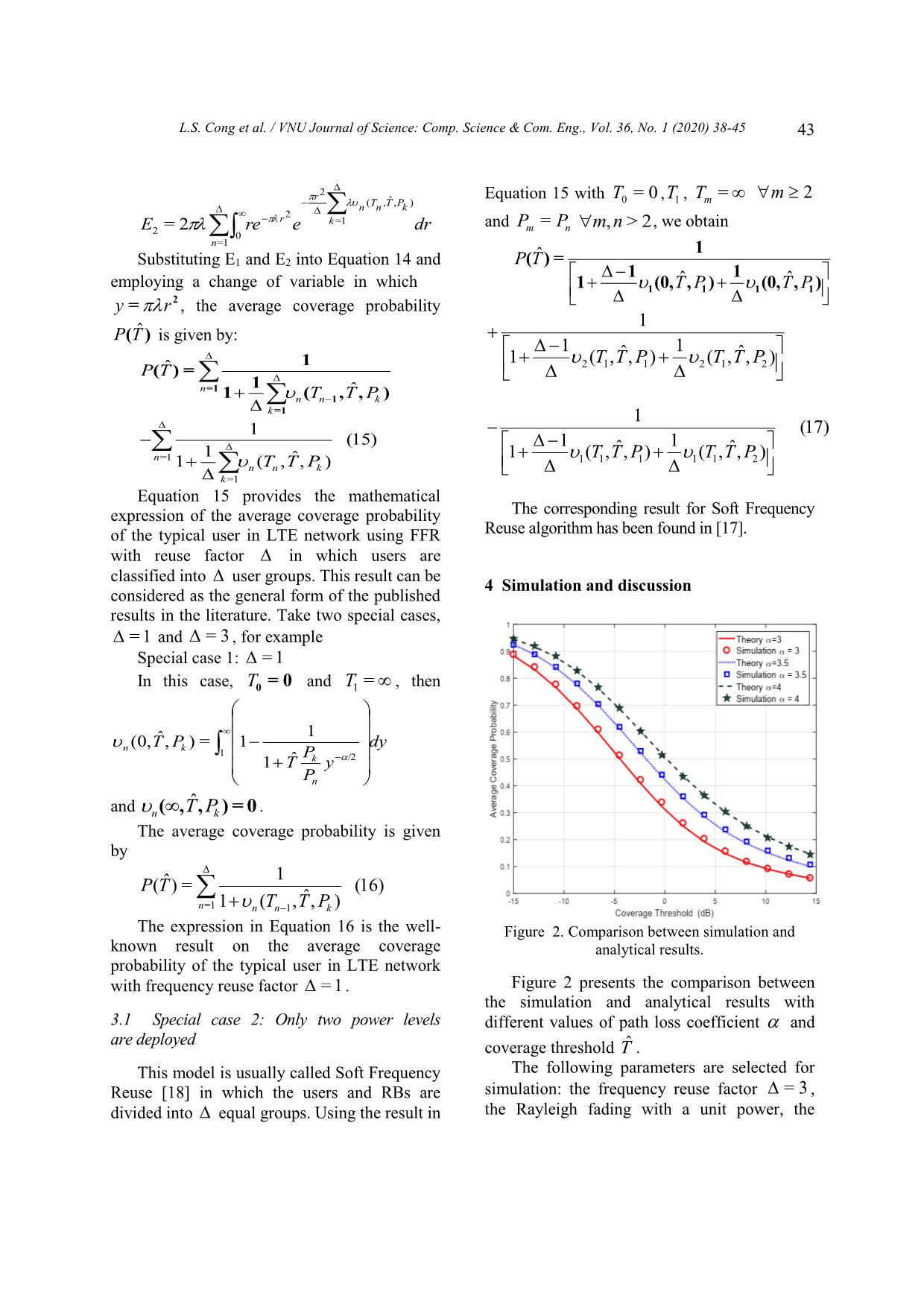
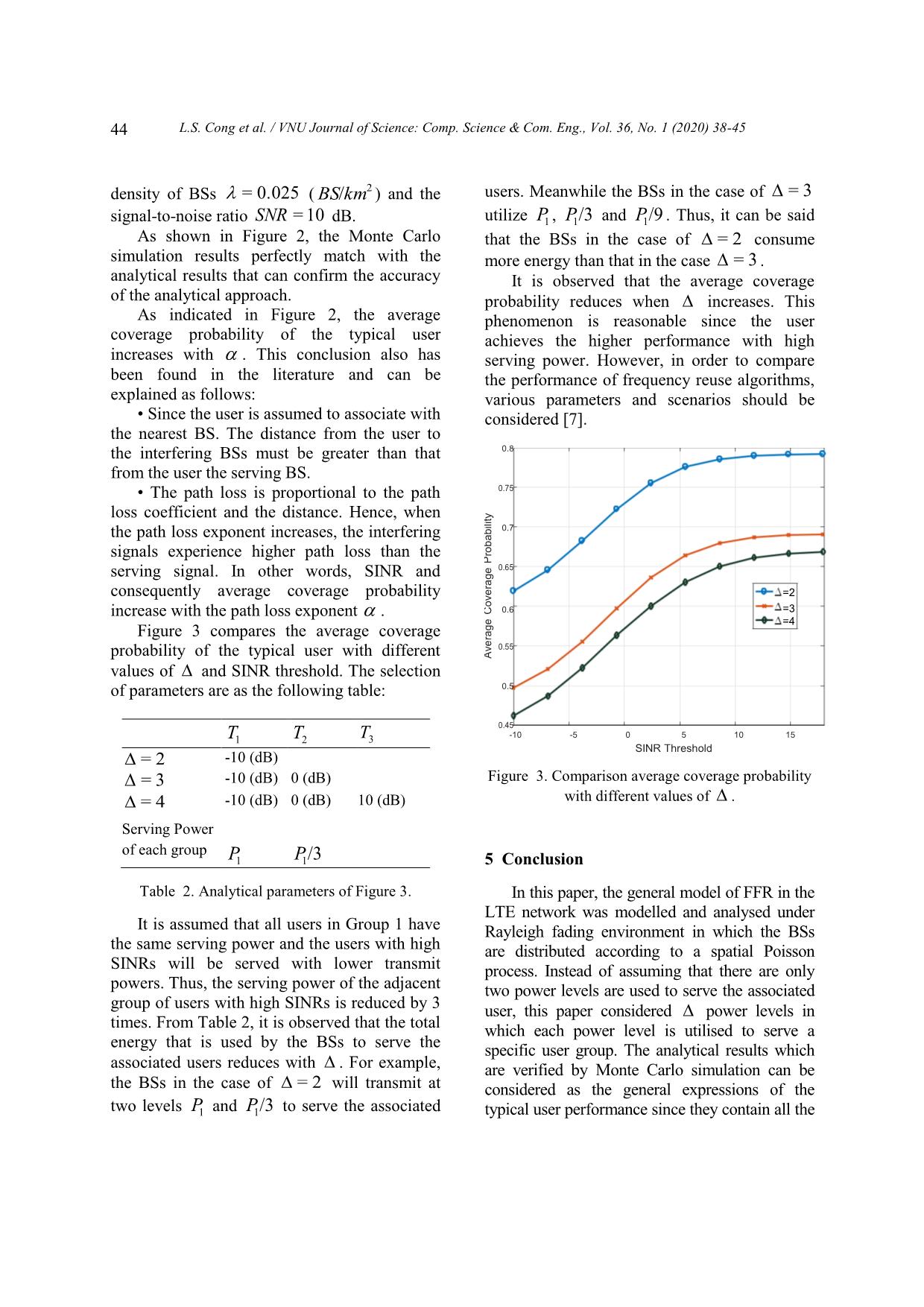
trol channels [4, 5] 
 number. 
for user classification purpose. Every BS is 
 Due to sharing the RBs between cells, each 
continuously transmitting downlink control 
 user experiences ICI from all neighbouring 
information, and subsequently each control 
 cells. The total ICI power at the typical user is 
channel experiences the ICI from all adjacent 
 given by: 
BSs. Furthermore, since all BSs are assumed to 
transmit on the control channels at the same IPgr=(4) 
power, the ICI of the measured SINR during kjj
 kj=1 k
this phase is given by. 
 in which k is the set of interfering BSs 
 IPgr=(1) ()o 
 0  jj transmitting at Pj power level. The density of 
 j 
 
 (o) BSs in k is . 
 where g j and rj are the channel power 
gain and distance between BS j and the user, Equation 4 can be considered as the general 
respectively. case of the well-known FFR algorithm 
 The reported SINR on the control channel is modelling in the literature. For examples: 
given by • When = 1, Equation 4 degrades into 
 ()o 
 Pg r I= Pgjj r (5) 
 SINR =2 (o ) (2) j 
  Pgjj r
 j  In Equation 5,  consists of all adjacent 
in which g and r is the channel power gain BSs. This equation has been found in the 
and the distance from the user to its serving BS. literature such as [15, 16]. 
 L.S. Cong et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 1 (2020) 38-45 41 
 • When only two power levels are deployed Therefore, the probability in which the 
(only one SINR threshold is required): for typical user is under the network coverage at a 
example group 1 is served by transmit power 
 given time slot is given by 
 P1 and 1 remaining groups are served by 
 PPTSINRT=(<<)
transmit power P2 , Equation 4 degrades into cnn  1
 n=1 (9) 
 1
 ˆ
 IPgrP=(6) gr12jjjj PSINRT(>) 
 jkj =1
 1 k It is reminded that the coverage probability 
 Due to the thinning properties of PPP [16], 
 in Equation 9 is a function of random variables 
each BS in 1 is distributed independently to 
 such as channel power gain g , g j , distance 
any BS in  ( j 1). Therefore, Equation 6 is 
 k from the user to other BSs. Thus, to obtain the 
rewritten as 
 average coverage probability of the typical user, 
 IPgrP=(7) gr12jjjj 
 the expected value of Pc should be computed. 
 jj 10
 Therefore, the average coverage probability of 
in which the density of BSs in 1 and 2 are 
 / and ( 1)/ respectively. the user in the network is defined as following 
 Equation 7 is exactly the ICI of Soft FR. equation: 
 The reported SINR on the data channel ˆ
 P() TEP =((<<) TSINRT nn 1
during the communication phase is given by n=1 (10)
 Pgr ˆ
 P(>)) SINRTn
 SINR =(8) 
 Using the definition of SINR in Equation 2, 
 Pgkjj r
 kj=1 
 k P(T < SINR < T )
 in which g and r is the channel power n 1 n 
gain and the distance from the user to its (o) 
serving BS. g r
 = P Tn 1 < (o) < Tn 
 g j rj 
 j  
3 Performance evaluation rr 
 =<<P TggTg (ooo )( )( )
 njnj 1 
 In this section, we derive the average jj rrjj
coverage probability of the typical user, which 
can be classified into one of groups. (a)
 At a given time slot, the user at a distance (o) 
 = exp Tn 1g j rj r 
 r from its serving BS is assigned to group j if j 
its downlink SINR satisfies Equation 3. The ()o 
 exp Tnjj grr (11) 
corresponding probability is j 
 P(T < SINR < T ) . (o)
 n 1 n in which (a) due to g has a exponential 
 The user in group j is under the network distribution. 
coverage if its SINR during the communication 
 Similarity, using the definition of SINR in 
phase, denoted by SINR , is greater than the 
 Equation 8, we have 
coverage threshold Tˆ . Thus, the coverage 
 P(SINR > Tˆ) 
probability is P(SINR > Tˆ) . 
42 L.S. Cong et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 1 (2020) 38-45 
 P gr Evaluating the fist element with notice that 
 = P( n > Tˆ)
 k is a subset of  , we divide  into 
 Pk g jrj
   independent subsets k with the densities of 
 k=1 j k 
 BSs are / . Thus, the first element in 
 ˆ Pk Equation 14 can be rewritten as follows: 
 = P g > T  g j rj r 
 k=1 P j  
 n k 
 ()b 1 1 
 Pk 
 =exp Tgrrˆ (12) E1 = E 
  jj   P r r 
 kj=1  P n=1 k=1 j  ˆ k
 k n k 1 T 1 T 
 n 1 
 Pn rj rj 
where (b) due to g is a exponential random 
 Employing the properties of the Probability 
variable. Generating Function [19], we obtain 
 Substituting Equations 11 and 12 into 
Equation 10, the average coverage probability 
 2  1 1 
 ˆ 1 r dr
 P(T ) is given by P j j 
 r ˆ k r r 
 1 T 1 Tn 1 
 P 
 n rj rj
 P E1 = E e
 ˆ k   
   exp Tg rr jj n=1 k =1
 k 1 
 Pn
 j k 
  E ()o (13) 
 exp Tgrrnjj 1 
 n 1 2
 j  Using a change of variable y = (r /r) , E 
 j 1
 ()o 
 exp Tnjj grr can be rewritten as follows 
 j  
 2 r2 1 1
 1 dy
 Pk /2 1 Ty /2
 Since all channel power gains are 1 1 Tyˆ n 1
 P
independent exponential random variables n
 Ee1 =  E 
whose the Moment Generating Function (MGF) n=1 k =1
 1
is M = E[e sx ] = , taking the expected 
 X 1 s 
 (o) Taking the expected value with respect to r , 
value of Equation with respect to g j and g j , 
 E is given by 
 ˆ 1
 PT() is obtained by 
 r2
  (T ,Tˆ,P )
 n n 1 k
 2 
  r k=1
 2  re e dr
 11  0
 E n=1
    
 n=1 P rr
 k=1 j k ˆ k j in which 
 11 TT n 1
 P r r
 n j j 
 1 1
 ˆ 
 11 n (Tn 1,T, Pk ) = 1 /2 dy
 E (14) 1 P /2 1 T y 
   P rr 1 Tˆ k y n 1
 n=1 k=1 jj k 11 TTˆ k 
 n Pn 
 Pn rr jj
 Similarly, the second element of Equation 14 is 
 given by 
 L.S. Cong et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 1 (2020) 38-45 43 
 r2 Equation 15 with T = 0 ,T , T = m 2 
  (T ,Tˆ,P ) 0 1 m
 n n k
 2 
  r k=1 and P = P , we obtain 
 E2 = 2  re e dr m n m,n > 2
  0
 n=1 1
 Substituting E and E into Equation 14 and PT()ˆ =
 1 2 11
employing a change of variable in which ˆˆ
 1(0,,)(0,,) 1111 TPTP
 2 
 yr=  , the average coverage probability 
 1
 PT()ˆ is given by: 
 1 1 
 1 1  (T ,Tˆ, P )  (T ,Tˆ, P )
 PT()ˆ = 2 1 1 2 1 2 
  1 
 n=1 1(,,)  TTP ˆ 
  nnk 1
 k=1 1
 1 (17)
 (15) 11
  1 1  (TTPTTP ,ˆˆ , ) ( , , )
 n=1 1(,,)  TTPˆ 1 1 1 1 1 2
  nnk 
 k=1
 Equation 15 provides the mathematical 
expression of the average coverage probability The corresponding result for Soft Frequency 
of the typical user in LTE network using FFR Reuse algorithm has been found in [17]. 
with reuse factor in which users are 
classified into user groups. This result can be 
 4 Simulation and discussion 
considered as the general form of the published 
results in the literature. Take two special cases, 
 = 1 and = 3 , for example 
 Special case 1: = 1 
 In this case, T0 =0 and T1 = , then 
 ˆ 1 
n (0,T, Pk ) = 1 dy
 1 P 
 1 Tˆ k y /2
 P 
 n 
 ˆ
and nk( ,TP , ) = 0 . 
 The average coverage probability is given 
by 
 1
 PT()ˆ =(16) 
 n=1 1(,,)  TTP ˆ
 nnk 1 
 The expression in Equation 16 is the well- Figure 2. Comparison between simulation and 
known result on the average coverage analytical results. 
probability of the typical user in LTE network 
with frequency reuse factor = 1. Figure 2 presents the comparison between 
 the simulation and analytical results with 
3.1 Special case 2: Only two power levels different values of path loss coefficient and 
are deployed coverage threshold Tˆ . 
 This model is usually called Soft Frequency The following parameters are selected for 
Reuse [18] in which the users and RBs are simulation: the frequency reuse factor = 3 , 
divided into equal groups. Using the result in the Rayleigh fading with a unit power, the 
44 L.S. Cong et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 1 (2020) 38-45 
density of BSs  = 0.025 ( BS/km2 ) and the users. Meanwhile the BSs in the case of = 3 
signal-to-noise ratio SN R = 10 dB. utilize P1 , P1/3 and P1/9 . Thus, it can be said 
 As shown in Figure 2, the Monte Carlo that the BSs in the case of = 2 consume 
simulation results perfectly match with the more energy than that in the case = 3 . 
analytical results that can confirm the accuracy It is observed that the average coverage 
of the analytical approach. probability reduces when increases. This 
 As indicated in Figure 2, the average phenomenon is reasonable since the user 
coverage probability of the typical user achieves the higher performance with high 
increases with . This conclusion also has serving power. However, in order to compare 
been found in the literature and can be the performance of frequency reuse algorithms, 
explained as follows: various parameters and scenarios should be 
 • Since the user is assumed to associate with considered [7]. 
the nearest BS. The distance from the user to 
the interfering BSs must be greater than that 0.8 
from the user the serving BS. 
 • The path loss is proportional to the path 0.75 
loss coefficient and the distance. Hence, when 
the path loss exponent increases, the interfering 0.7 
signals experience higher path loss than the 
 Probability
serving signal. In other words, SINR and 0.65 
 age
consequently average coverage probability =2 
 0.6 =3 
 Cover
increase with the path loss exponent . 
 =4 
 Figure 3 compares the average coverage 
 0.55 
probability of the typical user with different Average
values of and SINR threshold. The selection 
of parameters are as the following table: 0.5 
 0.45 
 T1 T2 T3 -10 -5 0 5 10 15 
 SINR Threshold 
 = 2 -10 (dB) 
 = 3 -10 (dB) 0 (dB) Figure 3. Comparison average coverage probability 
 = 4 -10 (dB) 0 (dB) 10 (dB) with different values of . 
 Serving Power 
 of each group 
 P1 P1/3 5 Conclusion 
 Table 2. Analytical parameters of Figure 3. In this paper, the general model of FFR in the 
 LTE network was modelled and analysed under 
 It is assumed that all users in Group 1 have Rayleigh fading environment in which the BSs 
the same serving power and the users with high are distributed according to a spatial Poisson 
SINRs will be served with lower transmit process. Instead of assuming that there are only 
powers. Thus, the serving power of the adjacent two power levels are used to serve the associated 
group of users with high SINRs is reduced by 3 user, this paper considered power levels in 
times. From Table 2, it is observed that the total which each power level is utilised to serve a 
energy that is used by the BSs to serve the specific user group. The analytical results which 
associated users reduces with . For example, are verified by Monte Carlo simulation can be 
the BSs in the case of = 2 will transmit at considered as the general expressions of the 
two levels P1 and P1/3 to serve the associated typical user performance since they contain all the 
 L.S. Cong et al. / VNU Journal of Science: Comp. Science & Com. Eng., Vol. 36, No. 1 (2020) 38-45 45 
related results in the literature. For practical Cellular Networks, IEEE Commun, Surveys & 
perspective, based on the relationships between Tutorials 15(4) (2013) 1642-1670. 
 https://doi.org/10.1109/SURV.2013.013013.00028. 
frequency reuse factor , SINR threshold T , 
 j [10] A. Busson1, I. Lahsen-Cherif2, Impact of resource 
density of BSs and the network performance that blocks allocation strategies on downlink 
were derived in the paper, the network designers interference and sir distributions in lte networks: 
can select appropriate values to obtain the desired A stochastic geometry approach, Wireless 
user performance. Communications and Mobile Computing. 
 [11] H. ElSawy, E. Hossain, M. Haenggi, Stochastic 
 Geometry for Modeling, Analysis and Design of 
Acknowledgments Multi-Tier and Cognitive Cellular Wireless 
 Networks: A Survey, IEEE Commun, Surveys 
 This work has been supported/partly Tutorials 15(3) (2013) 996-1019. 
supported by VNU University of Engineering https://doi.org/10.1109/SURV.2013.052213.00000. 
and Technology under project number [12] W. Bao, B. Liang, Stochastic Analysis of Uplink 
CN18.01. Interference in Two-Tier Femtocell Networks: 
 Open Versus Closed Access, IEEE Trans, 
 Wireless Commun. 14(11) (2015) 6200-6215. 
 https://doi.org/10.1109/TWC.2015.2450216 . 
References [13] H. Tabassum, Z. Dawy, E. Hossain, M.S. Alouini, 
 Interference Statistics and Capacity Analysis for 
 [1] Cisco, Cisco visual networking index: Global mobile Uplink Transmission in Two-Tier Small Cell 
 data traffic forecast update, 2015 - 2020, 2016. Networks: A Geometric Probability Approach, 
 [2] A.S. Hamza, S.S. Khalifa, H.S. Hamza, K. IEEE Trans, Wireless Commun 13(7) (2014) 
 Elsayed, A Survey on Inter-Cell Interference 3837-3852. 
 Coordination Techniques in OFDMA-Based 
 Cellular Networks, IEEE Commun, Surveys & [14] J.G. Andrews, F. Baccelli, R.K. Ganti, A tractable 
 Tutorials 15(4) (2013) 1642-1670 approach to coverage and rate in cellular networks, 
 [3] 3GPP TR 36.819 V11.1.0, Coordinated multi-point IEEE Transactions on Communications 59(11) 
 operation for LTE physical layer aspects, 2011. (2011) 3122-3134. 
 [4] 3GPP Release 10 V0.2.1, LTE-Advanced (3GPP [15] Y. Lin, W. Bao, W. Yu, B. Liang, Optimizing 
 Release 10 and beyond), 2014. User Association and Spectrum Allocation in 
 [5] 3GPP TS 36.211 V14.1.0, E-UTRA Physical HetNets: A Utility Perspective, IEEE J. Sel. Areas 
 Channels and Modulation, 2016. Commun. 33(6) (2015) 1025-1039. 
 [6] R. Ghaffar, R. Knopp, Fractional frequency reuse https://doi.org/10.1109/JSAC.2015.2417011. 
 and interference suppression for ofdma networks, [16] M. Haenggi, Stochastic Geometry for Wireless 
 in: 8th International Symposium on Modeling and Networks, Cambridge Univ, Press, November 2012. 
 Optimization in Mobile, Ad Hoc and Wireless [17] H. ElSawy, E. Hossain, M. Haenggi, Stochastic 
 Networks, 2010, pp. 273-277. Geometry for Modeling, Analysis and Design of 
 [7] Y. Kwon, O. Lee, J. Lee, M. Chung, Power Multi-Tier and Cognitive Cellular Wireless 
 Control for Soft Fractional Frequency Reuse in Networks: A Survey, IEEE Commun, Surveys 
 OFDMA System, Vol. 6018 of Lecture Notes in Tutorials 15(3) (2013) 996-1019. 
 Comput.Science, Springer Berlin Heidelberg, [18] Huawei, R1-050507: Soft Frequency Reuse 
 2010, book section 7 (2010) 63-71. Scheme for UTRAN LTE, in: 3GPP TSG RAN 
 [8] Enhancing LTE Cell-Edge Performance via WG1 Meeting #41, 2005. 
 PDCCH ICIC, in: FUJITSU NETWORK 
 [19] M.A. Stegun, I.A., Handbook of Mathematical 
 COMMUNICATIONS INC., 2011. 
 Functions with Formulas, Graphs and 
 [9] A.S. Hamza, S.S. Khalifa, H.S. Hamza, K. Mathematical Tables, 9th Edition, Dover 
 Elsayed, A Survey on Inter-Cell Interference Publications, 1972. 
 Coordination Techniques in OFDMA-Based 
4 
u