A force measuring microsystem bases on electrothermal v-shaped actuator

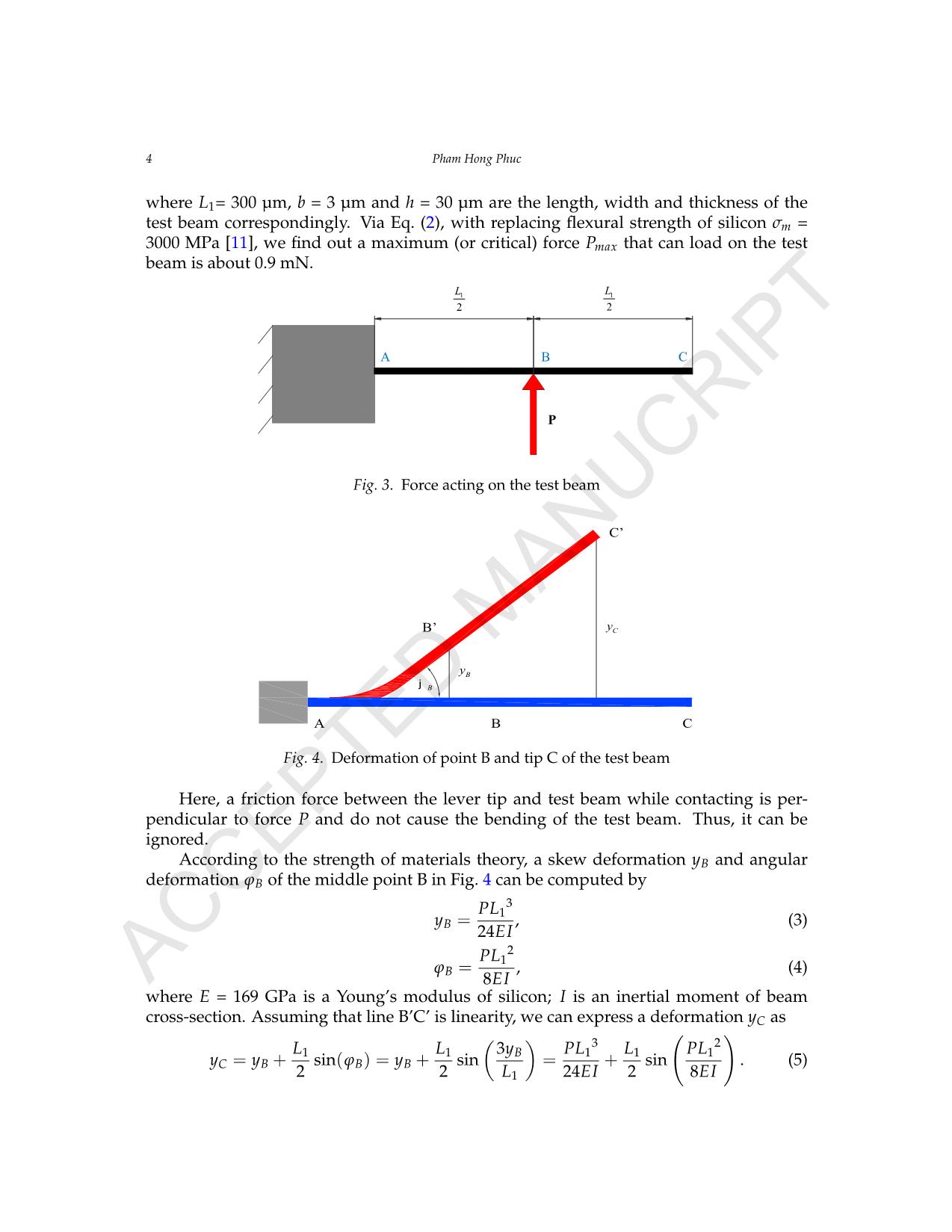
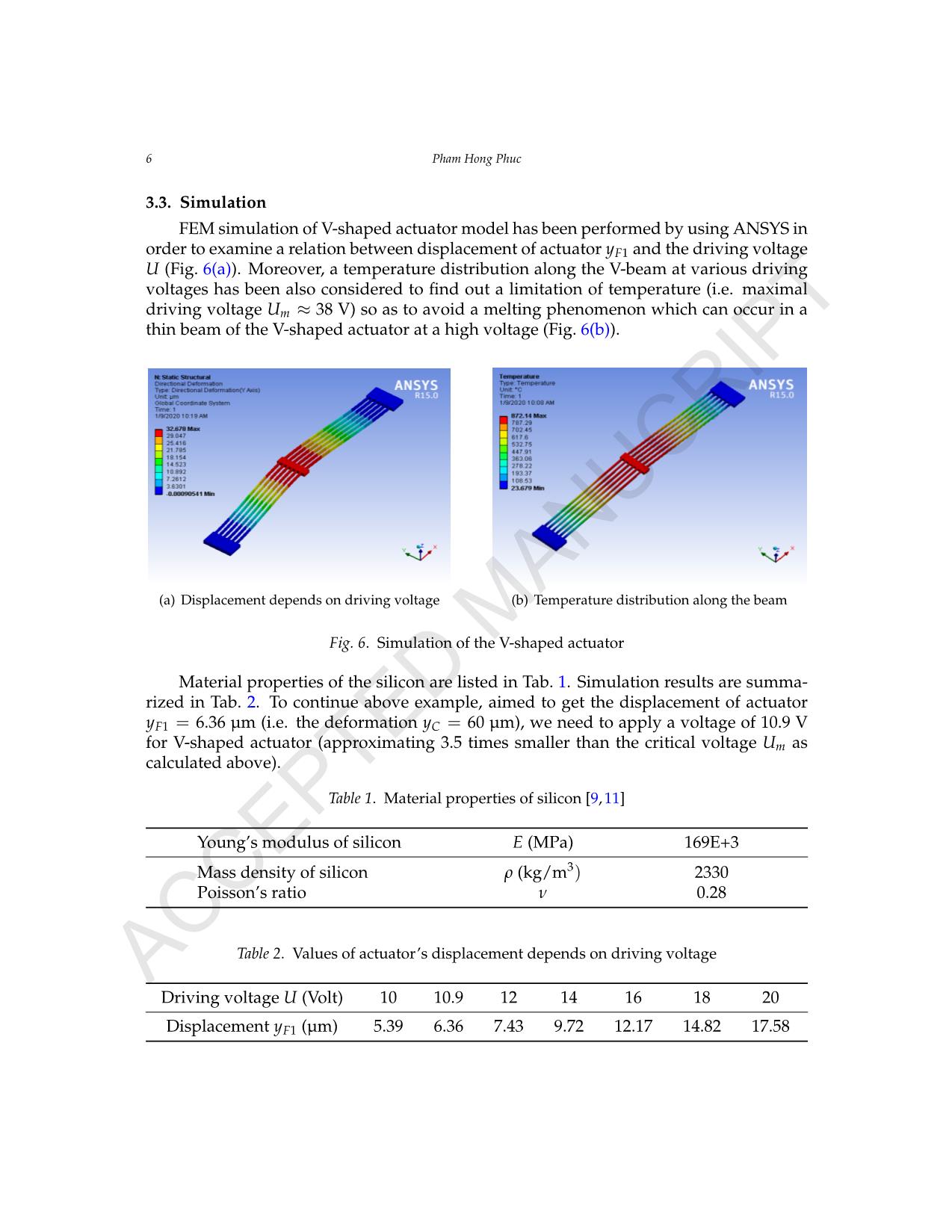
2
max
1
. .
3
h b
P
L
s
=
P
1
2
L 1
2
L
B CA
Bj
By
Cy
A B C
B’
C’
Fig. 4. Deformation of point B and tip C of the test beam
Here, a friction force between the lever tip and test beam while contacting is per-
pendicular to force P and do not cause the bending of the test beam. Thus, it can be
ignored.
According to the strength of materials theory, a skew deformation yB and angular
deformation ϕB of the middle point B in Fig. 4 can be computed by
yB =
PL13
24EI
, (3)
ϕB =
PL12
8EI
, (4)
where E = 169 GPa is a Young’s modulus of silicon; I is an inertial moment of beam
cross-section. Assuming that line B’C’ is linearity, we can express a deformation yC as
yC = yB +
L1
2
sin(ϕB) = yB +
L1
2
sin
(
3yB
L1
)
=
PL13
24EI
+
L1
2
sin
(
PL12
8EI
)
. (5)
AC
CE
PT
ED
 M
AN
UC
RI
PT
A force measuring microsystem bases on electrothermal V-shaped actuator 5
From Eqs. (3)–(5), if know the value of yC (via checking the ruler 5© by microscope), we
can calculate easily a deformation yB and the force P. As an example: assuming that
measured deformation yC = 60 µm, we get the deformation yB = 24.14 µm and the force
P is about 0.245 mN.
3.2. Relation between driving force of V-shaped actuator and deformation of test beam
Fig. 5 shows the schematic view of forces acting on the lever while working. Here,
and are elastic forces of the left and right springs; P′ = P is reaction force from the test
beam; F1 is a driving force of the actuator loading on the lever. We have the equilibrium
equation of moment around the articulated joint as followed
1
6
L2F1 =
1
10
L2Flx1 +
3
4
L2Flx2 + L2P, (6)
and the driving force of the actuator is
F1 =
3
5
ky1 +
9
2
ky2 + 6P. (7)
4 Pham Hong Phuc 
Here, a friction force between the lever tip and test beam while contacting is perpendicular to 
force P and do not cause the bending of the test beam. Thus, it can be ignored. 
According to the strength of materials theory, a skew deformation yB and angular deformation φB 
of the middle point B in Fig. 4 can be computed by: 
 (3) 
 (4) 
Where E = 169 GPa is a Young’s modulus f silicon; I = is an inertial moment of beam c oss-
section. Assuming that line B’C’ is linearity, we can express a deformation yC as: 
 (5) 
From equations (3-5), if know the value of yC (via checking the ruler … by microscope), we can 
calculate easily a deformation yB and the force P. As an example: assuming that measured deformation 
yC = 60 µm, we get the deformation yB = 24.14 µm and the force P is about 0.245 mN. 
3.2. Relation between driving force of V-shaped actuator and deformation of test beam 
Fig. 5. Forces act on the lever 
Fig. 5 shows the schematic view of forces acting on the lever while working. Here, and 
are elastic forces of the left and right springs; P’=P is reaction force from the test beam; F1 is 
a driving force of the actuator loading on the lever. We have the equilibrium equation of moment around 
the articulated joint as followed: 
 (6) 
And the driving force of the actuator is: (7) 
By substituting (3) into (7), we have: (8) 
3
1.
24 .B
P Ly
E I
=
2
1.
8 .B
P L
E I
j =
3.
12
h b
3 2
1 1 1 1 1
1
3. . ..sin( ) .sin .sin
2 2 24 . 2 8 .
B
C B B B
L L y P L L P Ly y y
L E I E I
j
Ê ˆÊ ˆ ˜˜ ÁÁ ˜˜= + = + = + ÁÁ ˜˜ ÁÁ ˜˜Á ÁË ¯ Ë ¯
1L
1
6
L
1
10
L
1
3
4
L
1lxF 2lxF
P
1F
L2
L2
L2
L2
’
1 1.lxF k y=
2 2.lxF k y=
2 1 2 1 2 2 2
1 1 3. . . .
6 10 4lx lx
L F L F L F L P= + +
1 1 2
3 9. . 6
5 2
F k y k y P= + +
1 1 1 3
1
3 1 9 3 24 .. ( ) . ( ) 6 .
5 10 2 4B B B
E IF k y g k y g y
L
È ˘ È ˘
Í ˙ Í ˙= + + + +Í ˙ Í ˙Î ˚ Î ˚
Fig. 5. Forces act on the lever
By substituting (3) into (7), we have
F1 =
3
5
k
[
1
10
(yB + g1)
]
+
9
2
k
[
3
4
(yB + g1)
]
+ 6yB
24EI
L31
, (8)
where k = 15.23 µN/µm is a stiffness of each spring obtained by simulation; and are the
deformation of left and right springs. Eq. (8) describes a relation between driving force
F1 and deformation yB at the middle of test beam. If yB = 24.14 µm, g1 = 2 µm and P
= 0.245 mN as mentioned above, we need the driving force of V-shaped actuator: F1 ≈
2.838 mN. Required displacement yF1 of the shuttle can be calculated as
yF1 =
(
yB + g1
6
)
+ g2, (9)
where g1 and g2 are the fabrication gaps and described as in Section 2.1. If we choose
g1 = g2 = 2 µm, the displacement of the shuttle should be equal or larger than 6.36 µm.
AC
CE
PT
ED
 M
AN
UC
RI
PT
6 Pham Hong Phuc
3.3. Simulation
FEM simulation of V-shaped actuator model has been performed by using ANSYS in
order to examine a relation between displacement of actuator yF1 and the driving voltage
U (Fig. 6(a)). Moreover, a temperature distribution along the V-beam at various driving
voltages has been also considered to find out a limitation of temperature (i.e. maximal
driving voltage Um ≈ 38 V) so as to avoid a melting phenomenon which can occur in a
thin beam of the V-shaped actuator at a high voltage (Fig. 6(b)).
 A Force Measuring Microsystem Bases on the Electrothermal V-shaped Actuator 5 
Where k = 15.23 µN/µm is a stiffness of each spring obtained by simulation; and 
 are the deformation of left and right springs. Equation (8) describes a relation between 
driving force F1 and deformation yB at the middle of test beam. If yB = 24.14 µm, g1 = 2 µm and P = 
0.245 mN as mentioned above, we need the driving force of V-shaped actuator: F1 ≈ 2.838 mN. 
Required displacement yF1 of the shuttle can be calculated as: 
 (9) 
Where g1 and g2 are the fabrication gaps and described as in the section 2.1. If we choose g1 = g2 = 2µm, 
the displacement of the shuttle should be equal or larger than 6.36 µm. 
3.3. Simulation 
FEM simulation f V-shaped actuator model has een perf rmed by using ANSYS in order to ex-
amine a relation betw en displa ement of actuator yF1 and the driving voltage U (Fig. 6a). Moreover, a 
temperature distribution along the -beam at various driving voltages has been also considered to find 
out a limitation of temperature (i.e. maximal driving voltage Um ≈ 38V ) so as to avoid a melting phe-
nomenon which can occur in a thin beam of the V-shaped actuator at a high voltage (Fig. 6b). 
(a) Displacement depends on driving voltage; (b) Temperature distribution along the beam; 
Fig. 6. Simulation of the V-shaped actuator 
Material properties of the silicon are listed in Table 1. Simulation results are summarized in 
Table 2. To continue above example, aimed to get the displacement of actuator yF1 = 6.36 µm (i.e. the 
deformation yC = 60 µm), we need to apply a voltage of 10.9 V for V-shaped actuator (approximating 3.5 
times smaller than the critical voltage Um as calculated above). 
Table 1. Material properties of silicon [8, 10] 
Young’s modulus of silicon E (MPa) 169E+3 
Mass density of silicon ρ (kg/m3) 2330 
Poisson’s ratio υ 0.28 
Table 2. Values of actuator’s displacement depends on driving voltage 
Driving voltage U (Volt) 10 10.9 12 14 16 18 20 
Displacement yF1 (µm) 5.39 6.36 7.43 9.72 12.17 14.82 17.58 
1 1
1 ( )
10 B
y y g= +
2 1
3 ( )
4 B
y y g= +
1
1 26
B
F
y gy g
Ê ˆ+ ˜Á= +˜Á ˜˜ÁË ¯
(a) Displacement depends on driving voltage
 A Force Measuring Microsystem Bases on the Electrothermal V-shaped Actuator 5 
Where k = 15.23 µN/µm is a stiffness of each spring obtained by simulation; and 
 are the deformation of left and right springs. Equation (8) describes a relation between 
driving force F1 and deformation yB at the middle of test beam. If yB = 24.14 µm, g1 = 2 µm and P = 
0.245 mN as mentioned above, we need the driving force of V-shaped actuator: F1 ≈ 2.838 mN. 
Required displacement yF1 of the shuttle can be calculated as: 
 (9) 
Where g1 and g2 are the fabrication gaps and described as in the section 2.1. If we choose g1 = g2 = 2µm, 
the displacement of the shuttle should be equal or larger than 6.36 µm. 
3.3. Simulation 
FEM simulation of V-sh p d actu or model has been perform d by using ANSYS in order to ex-
amine a relation between displacement of actuator yF1 nd the driving voltage U (Fig. 6a). Moreover, a 
temperature distribution along the V-beam t various driving voltages has been also considered to find 
out a limitation of temperatur (i.e. maximal driving voltag Um ≈ 38V ) so as to avoid a melting phe-
nome on which can occur in a thin beam of the V-shaped actuator at a igh voltage (Fig. 6b). 
(a) Displac ment depends on driving voltage; (b) Temperature distribution along the beam; 
Fig. 6. Simulation of the V-shaped actuator 
Material properties of the silicon are listed in Table 1. Simulation results are summarized in 
Table 2. To continue above example, aimed to get the displacement of actuator yF1 = 6.36 µm (i.e. the 
deformation yC = 60 µm), we need to apply a voltage of 10.9 V for V-shaped actuator (approximating 3.5 
times smaller than the critical voltage Um as calculated above). 
Table 1. Material properties of silicon [8, 10] 
Young’s modulus of silicon E (MPa) 169E+3 
Mass density of silicon ρ (kg/m3) 2330 
Poisson’s ratio υ 0.28 
Table 2. Values of actuator’s displacement depends on driving voltage 
Driving voltage U (Volt) 10 10.9 12 14 16 18 20 
Displacement yF1 (µm) 5.39 6.36 7.43 9.72 12.17 14.82 17.58 
1 1
1 ( )
10 B
y y g= +
2 1
3 ( )
4 B
y y g= +
1
1 26
B
F
y gy g
Ê ˆ+ ˜Á= +˜Á ˜˜ÁË ¯
(b) Temperature distribution along the beam
Fig. 6. Simulation of the V-shaped actuator
Material properti s of the silicon are liste in Tab. 1. Simul ti n results are su ma-
rized i Tab. 2. To continue above exampl , aimed to get the displacement of actu or
yF1 = 6.36 µm (i.e. the deformation yC = 60 µm), we need to apply a voltage of 10.9 V
for V-shaped actuator (approximating 3.5 times smaller than the critical voltage Um as
calculated above).
Table 1. Material properties of silicon [9, 11]
Young’s modulus of silicon E (MPa) 169E+3
Mass density of silicon ρ (kg/m3) 2330
Poisson’s ratio ν 0.28
Table 2. Values of actuator’s displacement depends on driving voltage
Driving voltage U (Volt) 10 10.9 12 14 16 18 20
Displacement yF1 (µm) 5.39 6.36 7.43 9.72 12.17 14.82 17.58
AC
CE
PT
ED
MA
NU
CR
IP
T
A force measuring microsystem bases on electrothermal V-shaped actuator 7
4. CONCLUSIONS
This paper presents design and calculation of new force measuring microsystem
(FMMS) with the additional amplifying mechanism which allows to increasing the dis-
placement of the test beam up to 6 times than before [10]. Results can be summarized as
below:
Amplifying displacement of the lever tip can be measured more exactly by using
the ruler located near the free end of the cantilever test beam. Furthermore, two springs
connected to the lever can help it return to the initial position easier while the driving
voltage goes to zero.
The dependence of the driving force of actuator F1 as well as its displacement yF1
on the deformation of test beam yB is established in the equations from (6) to (9). In
other words, knowing the value of yC enable to find yB and compute accurately the
needed driving force F1 loaded on the lever. Thus, a corresponding voltage applying
for V-shaped actuator will be determined.
Distribution of temperature along the thin beam has been solved by simulation. A
critical driving voltage Um (in this case Um ≈ 38 V) is also proposed in order to avoid the
failure of V-shaped beam.
Because of simple fabrication technology and low cost, this system with cover size
of 2× 2 (mm2) can be developed and integrated to micro force-measurement device, not
only for V-shaped actuator, but also for others such as electrostatic or piezoelectric actu-
ator. Besides, it can be used widely to evaluate and check some mechanical properties of
silicon or of other materials (example: failure load and allowable bending/tensile/com-
pressive stress) in micro devices.
ACKNOWLEDGMENT
This research is funded by Vietnam National Foundation for Science and Technology
Development (NAFOSTED) under grant number 107.01-2019.05.
REFERENCES
[1] P. H. Pham, D. V. Dao, S. Amaya, R. Kitada, and S. Sugiyama. Straight movement
of micro containers based on ratchet mechanisms and electrostatic comb-drive actu-
ators. Journal of Micromechanics and Microengineering, 16, (12), (2006), pp. 2532–2538.
https://doi.org/10.1088/0960-1317/16/12/003.
[2] D. V. Dao, P. H. Pham, and S. Sugiyama. Multimodule micro transportation system based
on electrostatic comb-drive actuator and ratchet mechanism. Journal of Microelectromechanical
Systems, 20, (1), (2010), pp. 140–149. https://doi.org/10.1109/jmems.2010.2090503.
[3] V. L. Huy, S. Kamiya, J. Gaspar, and O. Paul. Statistical characterization of fracture
strength and fatigue lifetime of polysilicon thin films with different stress concentration
fields. Journal of Solid Mechanics and Materials Engineering, 6, (11), (2012), pp. 1013–1029.
https://doi.org/10.1299/jmmp.6.1013.
[4] M. Naraghi and I. Chasiotis. A mems platform for mechanical testing of soft nanofibers and
nanowires. Technical report, University of Illinois at Urbana Champaign, (2007).
[5] V. L. Huy, S. Kamiya, K. Nagayoshi, H. Izumi, J. Gaspar, and O. Paul. A prediction scheme
of the static fracture strength of MEMS structures based on the characterization of damage
AC
CE
PT
ED
 M
AN
UC
RI
PT
8 Pham Hong Phuc
distribution on a processed surface. Journal of Micromechanics and Microengineering, 23, (4),
(2013). https://doi.org/10.1088/0960-1317/23/4/045008.
[6] H. Conrad, H. Schenk, B. Kaiser, S. Langa, M. Gaudet, K. Schimmanz, M. Stolz, and M. Lenz.
A small-gap electrostatic micro-actuator for large deflections. Nature Communications, 6, (1),
(2015), pp. 1–7. https://doi.org/10.1038/ncomms10078.
[7] A. M. Ousaid, S. Haliyo, S. Re´gnier, and V. Hayward. Micro-force sensor by active control of a
comb-drive. In 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics,
IEEE, (2013), pp. 612–617. https://doi.org/10.1109/aim.2013.6584160.
[8] P. H. Phuc, D. K. Toan, D. B. Lam, N. T. Khoa, and N. T. Dung. Design and fabrication of
the trapezoidal electrostatic comb-drive actuator. Vietnam Journal of Mechanics, 34, (4), (2012),
pp. 261–269. https://doi.org/10.15625/0866-7136/34/4/2338.
[9] P. H. Pham, T. K. Dinh, L. B. Dang, K. T. Nguyen, and D. V. Dao. Micro cam system driven by
electrostatic comb-drive actuators based on SOI-MEMS technology. Microsystem Technologies,
21, (3), (2015), pp. 699–706. https://doi.org/10.1007/s00542-014-2086-y.
[10] P. H. Pham, K. T. Nguyen, and L. B. Dang. Design and performance of a high loading
electrostatic micro linear motor. Microsystem Technologies, 21, (11), (2015), pp. 2469–2474.
https://doi.org/10.1007/s00542-014-2392-4.
[11] J. J. Allen. MEMS design. Taylor & Francis Group, LLC, (2005).
AC
CE
PT
ED
 M
AN
UC
RI
PT